Conjunto (música)

Un conjunto ( conjunto de tonos , conjunto de clases de tonos , clase de conjunto , forma de conjunto , género de conjunto , colección de tonos ) en teoría musical , como en matemáticas y en el lenguaje general, es una colección de objetos. En contextos musicales, el término se aplica tradicionalmente con mayor frecuencia a colecciones de tonos o clases de tonos , pero los teóricos han extendido su uso a otros tipos de entidades musicales, de modo que se puede hablar de conjuntos de duraciones o timbres , por ejemplo. [2]
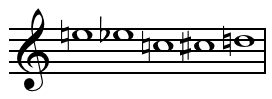

Un conjunto por sí mismo no posee necesariamente ninguna estructura adicional, como un ordenamiento o una permutación . Sin embargo, a menudo es musicalmente importante considerar conjuntos que están equipados con una relación de orden (llamados segmentos ); en tales contextos, los conjuntos desnudos a menudo se denominan "desordenados", para enfatizar. [4]
Los conjuntos de dos elementos se denominan díadas , los conjuntos de tres elementos se denominan tricords (ocasionalmente "tríadas", aunque esto se confunde fácilmente con el significado tradicional de la palabra tríada ). Los conjuntos de cardinalidades superiores se denominan tetracords (o tétradas), pentacords (o péntadas), hexacords (o hexadas), heptacords (heptadas o, a veces, mezclando raíces latinas y griegas, "septacords"), [5] octacords (octadas), nonacords (nonadas), decacords (decadas), undecacords y, finalmente, dodecacords .
Un conjunto de puntos de tiempo es un conjunto de duración donde la distancia en unidades de tiempo entre puntos de ataque, o puntos de tiempo, es la distancia en semitonos entre clases de tono. [6]
De serie
Sin embargo, en la teoría de la música serial , algunos autores [ palabras ambiguas ] (especialmente Milton Babbitt [7] [ página necesaria ] [ se necesita cita para verificar ] ) usan el término "conjunto" donde otros usarían "fila" o "serie", es decir, para denotar una colección ordenada (como una fila de doce tonos ) utilizada para estructurar una obra. Estos autores [ palabras ambiguas ] hablan de "conjuntos de doce tonos", "conjuntos de puntos temporales", "conjuntos derivados", etc. (ver más abajo). Este es un uso diferente del término "conjunto" del descrito anteriormente (y al que se hace referencia en el término " teoría de conjuntos ").
Para estos autores, una forma de conjunto ( o forma de fila ) es una disposición particular de un conjunto ordenado de este tipo: la forma primaria (orden original), inversa (al revés), retrógrada (hacia atrás) y retrógrada inversa (al revés y al revés). [2]
Un conjunto derivado es aquel que se genera o deriva de operaciones consistentes sobre un subconjunto, por ejemplo el Concierto de Webern , Op. 24, en el que los tres últimos subconjuntos se derivan del primero: [8]
Esto se puede representar numéricamente como los números enteros del 0 al 11:
0 11 3 4 8 7 9 5 6 1 2 10
El primer subconjunto (BB ♭ D) es:
0 11 3 forma prima, cadena de intervalo = ⟨−1 +4⟩El segundo subconjunto (E ♭ GF ♯ ) es el inverso retrógrado del primero, transpuesto un semitono hacia arriba:
3 11 0 retrógrado, intervalo-cadena = ⟨−4 +1⟩ mod 12 3 7 6 inversa, cadena de intervalo = ⟨+4 −1⟩ mod 12+ 1 1 1 ------= 4 8 7
El tercer subconjunto (G ♯ EF) es el retrógrado del primero, transpuesto hacia arriba (o hacia abajo) seis semitonos:
3 11 0 retrógrado+ 6 6 6 ------ 9 5 6
Y el cuarto subconjunto (CC ♯ A) siendo el inverso del primero, transpuesto un semitono hacia arriba:
0 11 3 forma prima, vector de intervalo = ⟨−1 +4⟩ mod 12 0 1 9 inversa, cadena de intervalo = ⟨+1 −4⟩ mod 12+ 1 1 1 ------- 1 2 10
Cada uno de los cuatro tricordios (conjuntos de 3 notas) muestra una relación que puede hacerse evidente mediante cualquiera de las cuatro operaciones de fila seriales y, por lo tanto, crea ciertas invariancias . Estas invariancias en la música serial son análogas al uso de tonos comunes y acordes comunes en la música tonal. [ cita requerida ]
No serial



El concepto fundamental de un conjunto no serial es que es una colección desordenada de clases de tono . [9]
La forma normal de un conjunto es el ordenamiento más compacto de las notas en un conjunto. [10] Tomlin define el ordenamiento "más compacto" como aquel en el que "el mayor de los intervalos entre dos notas consecutivas cualesquiera está entre la primera y la última nota enumerada". [10] Por ejemplo, el conjunto (0,2) (una segunda mayor ) está en forma normal mientras que el conjunto (0,10) (una séptima menor , la inversión de una segunda mayor) no lo está, siendo su forma normal (10,0).
En lugar de la forma "original" (sin transponer, sin invertir) del conjunto, la forma prima puede considerarse la forma normal del conjunto o la forma normal de su inversión, la que esté más compacta. [11] Forte (1973) y Rahn (1980) enumeran las formas primas de un conjunto como la versión más compactada a la izquierda posible del conjunto. Forte empaqueta desde la izquierda y Rahn empaqueta desde la derecha ("haciendo que los números pequeños sean más pequeños", en lugar de hacer "los números más grandes ... más pequeños" [12] ). Durante muchos años se aceptó que solo había cinco casos en los que los dos algoritmos difieren. [13] Sin embargo, en 2017, el teórico musical Ian Ring descubrió que hay una sexta clase de conjunto donde los algoritmos de Forte y Rahn llegan a diferentes formas primas. [14] Ian Ring también estableció un algoritmo mucho más simple para calcular la forma prima de un conjunto, [14] que produce los mismos resultados que el algoritmo más complicado publicado anteriormente por John Rahn.
Vectores
Véase también
Referencias
- ^ Whittall, Arnold (2008). Introducción al serialismo en Cambridge , pág. 165. Nueva York: Cambridge University Press. ISBN 978-0-521-68200-8 (pbk).
- ^ ab Wittlich, Gary (1975). "Conjuntos y procedimientos de ordenación en la música del siglo XX", Aspectos de la música del siglo XX , pág. 475. Wittlich, Gary (ed.). Englewood Cliffs, Nueva Jersey: Prentice-Hall. ISBN 0-13-049346-5 .
- ^ Whittall (2008), pág. 127.
- ^ Morris, Robert (1987). Composición con clases de altura: una teoría del diseño compositivo , pág. 27. Yale University Press. ISBN 0-300-03684-1 .
- ^ Por ejemplo, Rahn (1980), 140.
- ^ Wittlich (1975), pág. 476.
- ^ Véase cualquiera de sus escritos sobre el sistema de doce tonos, prácticamente todos los cuales están reimpresos en The Collected Essays of Milton Babbitt , S. Peles et al., eds. Princeton University Press, 2003. ISBN 0-691-08966-3 .
- ^ Wittlich (1975), pág. 474.
- ^ John Rahn , Basic Atonal Theory (Nueva York: Longman; Londres y Toronto: Prentice Hall International, 1980), pp.27–28. ISBN 0-582-28117-2 (Longman); ISBN 0-02-873160-3 (Prentice Hall International). Reimpreso en 1987 (Nueva York: Schirmer Books; Londres: Collier Macmillan, 1980), p.27. ISBN 0-02-873160-3 .
- ^ de Tomlin, Jay. "Todo sobre la teoría de conjuntos: ¿Qué es la forma normal?", JayTomlin.com .
- ^ Tomlin, Jay. "Todo sobre la teoría de conjuntos: ¿Qué es la forma prima?", JayTomlin.com .
- ^ Nelson, Paul (2004). "Dos algoritmos para calcular la forma prima". ComposerTools.com . Archivado desde el original el 23 de diciembre de 2017.
{{cite web}}: CS1 maint: URL no apta ( enlace ) - ^ Tsao, Ming (2007). Intervalos musicales abstractos: teoría de grupos para la composición y el análisis , pág. 99, n. 32. ISBN 9781430308355. Algoritmos dados en Morris, Robert (1991). Apuntes de clase para la teoría de la música atonal , pág. 103. Frog Peak Music.
- ^ ab "Un estudio de escalas musicales por Ian Ring".
Lectura adicional
- Schuijer, Michiel (2008). Análisis de la música atonal: teoría de conjuntos de clases de alturas y sus contextos . ISBN 978-1-58046-270-9 .
Enlaces externos
- "Calculadora de teoría de conjuntos", JayTomlin.com . Calcula la forma normal, la forma prima, el número de Forte y el vector de clase de intervalo para un conjunto dado y viceversa.
- "Calculadora de conjuntos de PC" , MtA.Ca.
