Péndulo

Un péndulo es un dispositivo hecho de un peso suspendido de un pivote para que pueda oscilar libremente. [1] Cuando un péndulo se desplaza lateralmente desde su posición de reposo, de equilibrio , está sujeto a una fuerza restauradora debido a la gravedad que lo acelerará de regreso a la posición de equilibrio. Cuando se libera, la fuerza restauradora que actúa sobre la masa del péndulo hace que oscile alrededor de la posición de equilibrio, balanceándose hacia adelante y hacia atrás. El tiempo para un ciclo completo, un balanceo hacia la izquierda y un balanceo hacia la derecha, se llama período . El período depende de la longitud del péndulo y también en un ligero grado de la amplitud , el ancho de la oscilación del péndulo.
El movimiento regular de los péndulos se utilizó para medir el tiempo y fue la tecnología de medición del tiempo más precisa del mundo hasta la década de 1930. [2] El reloj de péndulo inventado por Christiaan Huygens en 1656 se convirtió en el cronómetro estándar del mundo, utilizado en hogares y oficinas durante 270 años, y alcanzó una precisión de aproximadamente un segundo por año antes de ser reemplazado como estándar de tiempo por el reloj de cuarzo en la década de 1930. Los péndulos también se utilizan en instrumentos científicos como acelerómetros y sismómetros . Históricamente se utilizaron como gravímetros para medir la aceleración de la gravedad en estudios geofísicos, e incluso como un estándar de longitud. La palabra péndulo es neolatina , del latín pendulus , que significa ' colgar ' . [3]
Péndulo doble

En física y matemáticas , en el área de sistemas dinámicos , un péndulo doble también conocido como péndulo caótico es un péndulo con otro péndulo unido a su extremo, formando un sistema físico simple que exhibe un rico comportamiento dinámico con una fuerte sensibilidad a las condiciones iniciales . [4] El movimiento de un péndulo doble está gobernado por un conjunto de ecuaciones diferenciales ordinarias acopladas y es caótico .
Péndulo de gravedad simple
El péndulo de gravedad simple [5] es un modelo matemático idealizado de un péndulo. [6] [7] [8] Se trata de un peso (o péndulo ) en el extremo de una cuerda sin masa suspendida de un pivote, sin fricción . Cuando se le da un empujón inicial, oscilará hacia adelante y hacia atrás con una amplitud constante . Los péndulos reales están sujetos a la fricción y al arrastre del aire , por lo que la amplitud de sus oscilaciones disminuye.
Periodo de oscilación
El período de oscilación de un péndulo de gravedad simple depende de su longitud , de la fuerza de gravedad local y, en pequeña medida, del ángulo máximo en el que el péndulo oscila con respecto a la vertical, θ 0 , llamado amplitud . [9] Es independiente de la masa de la plomada. Si la amplitud se limita a oscilaciones pequeñas, [Nota 1] el período T de un péndulo simple, el tiempo que tarda en completar un ciclo, es: [10]
| ( 1 ) |
donde es la longitud del péndulo y es la aceleración local de la gravedad .
En oscilaciones pequeñas, el período de oscilación es aproximadamente el mismo para oscilaciones de diferente tamaño: es decir, el período es independiente de la amplitud . Esta propiedad, llamada isocronismo , es la razón por la que los péndulos son tan útiles para medir el tiempo. [11] Las oscilaciones sucesivas del péndulo, incluso si cambian de amplitud, toman la misma cantidad de tiempo.
Para amplitudes mayores , el período aumenta gradualmente con la amplitud, por lo que es más largo que el dado por la ecuación (1). Por ejemplo, en una amplitud de θ 0 = 0,4 radianes (23°) es 1% más grande que lo dado por (1). El período aumenta asintóticamente (hasta el infinito) a medida que θ 0 se acerca a π radianes (180°), porque el valor θ 0 = π es un punto de equilibrio inestable para el péndulo. El período verdadero de un péndulo de gravedad simple ideal se puede escribir en varias formas diferentes (ver péndulo (mecánica) ), un ejemplo es la serie infinita : [12] [13] donde está en radianes.
La diferencia entre este período verdadero y el período para pequeñas oscilaciones (1) se denomina error circular . En el caso de un reloj de pie típico cuyo péndulo tiene una oscilación de 6° y, por lo tanto, una amplitud de 3° (0,05 radianes), la diferencia entre el período verdadero y la aproximación de ángulo pequeño (1) asciende a unos 15 segundos por día.
Para pequeñas oscilaciones, el péndulo se aproxima a un oscilador armónico , y su movimiento en función del tiempo, t , es aproximadamente un movimiento armónico simple : [6] donde es un valor constante, que depende de las condiciones iniciales .
En el caso de péndulos reales, el período varía ligeramente en función de factores como la flotabilidad y la resistencia viscosa del aire, la masa de la cuerda o varilla, el tamaño y la forma del cuerpo y cómo está unido a la cuerda, y la flexibilidad y el estiramiento de la cuerda. [12] [14] En aplicaciones de precisión, puede ser necesario aplicar correcciones para estos factores a la ecuación (1) para obtener el período con precisión.
Un péndulo amortiguado y accionado es un sistema caótico . [ cita requerida ]
Péndulo compuesto
Cualquier cuerpo rígido oscilante que pueda girar libremente alrededor de un eje horizontal fijo se denomina péndulo compuesto o péndulo físico . Un péndulo compuesto tiene el mismo período que un péndulo de gravedad simple de longitud , llamada longitud equivalente o radio de oscilación , igual a la distancia desde el pivote hasta un punto llamado centro de oscilación . [15] Este punto se encuentra debajo del centro de masa del péndulo, a una distancia que depende de la distribución de masa del péndulo. Si la mayor parte de la masa se concentra en un cuerpo relativamente pequeño en comparación con la longitud del péndulo, el centro de oscilación está cerca del centro de masa. [16]
Se puede demostrar que el radio de oscilación o longitud equivalente de cualquier péndulo físico es
donde es el momento de inercia del péndulo respecto del punto de pivote , es la masa total del péndulo y es la distancia entre el punto de pivote y el centro de masas . Sustituyendo esta expresión en (1) anterior, el período de un péndulo compuesto viene dado por para oscilaciones suficientemente pequeñas. [17]
Por ejemplo, una varilla rígida uniforme de longitud que pivotea sobre un extremo tiene un momento de inercia . El centro de masa se encuentra en el centro de la varilla, por lo que al sustituir estos valores en la ecuación anterior se obtiene . Esto demuestra que un péndulo de varilla rígida tiene el mismo período que un péndulo simple de dos tercios de su longitud.
Christiaan Huygens demostró en 1673 que el punto de pivote y el centro de oscilación son intercambiables. [18] Esto significa que si cualquier péndulo se da vuelta y se balancea desde un pivote ubicado en su centro de oscilación anterior, tendrá el mismo período que antes y el nuevo centro de oscilación estará en el antiguo punto de pivote. En 1817, Henry Kater utilizó esta idea para producir un tipo de péndulo reversible, ahora conocido como péndulo Kater , para mejorar las mediciones de la aceleración debida a la gravedad.
Historia

Uno de los primeros usos conocidos de un péndulo fue un dispositivo sismómetro del siglo I del científico chino de la dinastía Han, Zhang Heng . [19] Su función era balancear y activar una de una serie de palancas después de ser perturbada por el temblor de un terremoto lejano. [20] Liberada por una palanca, una pequeña bola caería del dispositivo en forma de urna en una de las ocho bocas de sapos de metal debajo, en los ocho puntos de la brújula, lo que significa la dirección en la que se localizó el terremoto. [20]
Muchas fuentes [21] [22] [23] [24] afirman que el astrónomo egipcio del siglo X Ibn Yunus utilizó un péndulo para medir el tiempo, pero este fue un error que se originó en 1684 con el historiador británico Edward Bernard . [25] [26] [27] [28]
Durante el Renacimiento , se utilizaban grandes péndulos accionados manualmente como fuentes de energía para máquinas alternativas manuales, como sierras, fuelles y bombas. [29]
1602: La investigación de Galileo
El científico italiano Galileo Galilei fue el primero en estudiar las propiedades de los péndulos, comenzando alrededor de 1602. [30] El primer interés registrado en los péndulos hecho por Galileo fue alrededor de 1588 en sus notas publicadas póstumamente tituladas Sobre el movimiento , [31] [32] en las que señaló que los objetos más pesados continuarían oscilando durante una mayor cantidad de tiempo que los objetos más ligeros. El primer informe existente de su investigación experimental está contenido en una carta a Guido Ubaldo dal Monte, desde Padua, fechada el 29 de noviembre de 1602. [33] Su biógrafo y estudiante, Vincenzo Viviani , afirmó que su interés había sido despertado alrededor de 1582 por el movimiento oscilante de un candelabro en la Catedral de Pisa . [34] [35] Galileo descubrió la propiedad crucial que hace que los péndulos sean útiles como cronometradores, llamada isocronismo; el período del péndulo es aproximadamente independiente de la amplitud o ancho de la oscilación. [36] También descubrió que el período es independiente de la masa de la plomada y proporcional a la raíz cuadrada de la longitud del péndulo. Fue el primero en emplear péndulos de oscilación libre en aplicaciones de cronometraje simples. En 1602, Santorio Santori inventó un dispositivo que medía el pulso de un paciente por la longitud de un péndulo; el pulsilogium . [37] En 1641, Galileo dictó a su hijo Vincenzo un diseño para un mecanismo que mantuviera un péndulo oscilando, que ha sido descrito como el primer reloj de péndulo; [36] Vincenzo comenzó la construcción, pero no la había completado cuando murió en 1649. [38]
1656: El reloj de péndulo
En 1656, el científico holandés Christiaan Huygens construyó el primer reloj de péndulo . [39] Esto representó una gran mejora con respecto a los relojes mecánicos existentes; su máxima precisión mejoró de alrededor de 15 minutos de desviación al día a alrededor de 15 segundos al día. [40] Los péndulos se extendieron por Europa a medida que los relojes existentes fueron equipados con ellos. [41]
El científico inglés Robert Hooke estudió el péndulo cónico alrededor de 1666, que consiste en un péndulo que puede oscilar libremente en dos dimensiones, con la masa girando en un círculo o elipse. [42] Utilizó los movimientos de este dispositivo como modelo para analizar los movimientos orbitales de los planetas . [43] Hooke sugirió a Isaac Newton en 1679 que los componentes del movimiento orbital consistían en un movimiento inercial a lo largo de una dirección tangente más un movimiento de atracción en la dirección radial. Esto jugó un papel en la formulación de Newton de la ley de la gravitación universal . [44] [45] Robert Hooke también fue responsable de sugerir ya en 1666 que el péndulo podría usarse para medir la fuerza de la gravedad. [42]
Durante su expedición a Cayena , Guayana Francesa , en 1671, Jean Richer descubrió que un reloj de péndulo tenía 2+1 ⁄ 2 minutos por día más lento en Cayena que en París. De esto dedujo que la fuerza de gravedad era menor en Cayena. [46] [47] En 1687, Isaac Newton en Principia Mathematica demostró que esto se debía a que la Tierra no era una esfera verdadera sino ligeramente achatada (aplanada en los polos) por el efecto de la fuerza centrífuga debido a su rotación, lo que hacía que la gravedad aumentara con la latitud . [48] Se comenzaron a llevar péndulos portátiles en viajes a tierras lejanas, como gravímetros de precisión para medir la aceleración de la gravedad en diferentes puntos de la Tierra, lo que finalmente resultó en modelos precisos de la forma de la Tierra . [49]
1673: HuygensOscilador del reloj
En 1673, 17 años después de que inventara el reloj de péndulo, Christiaan Huygens publicó su teoría del péndulo, Horologium Oscillatorium sive de motu pendulorum . [50] [51] Marin Mersenne y René Descartes habían descubierto alrededor de 1636 que el péndulo no era del todo isócrono; su período aumentaba algo con su amplitud. [52] Huygens analizó este problema determinando qué curva debe seguir un objeto para descender por gravedad al mismo punto en el mismo intervalo de tiempo, independientemente del punto de partida; la llamada curva tautocrona . Mediante un método complicado que fue un uso temprano del cálculo , demostró que esta curva era una cicloide , en lugar del arco circular de un péndulo, [53] confirmando que el péndulo no era isócrono y que la observación de isocronismo de Galileo era precisa solo para pequeñas oscilaciones. [54] Huygens también resolvió el problema de cómo calcular el período de un péndulo de forma arbitraria (llamado péndulo compuesto ), descubriendo el centro de oscilación y su intercambiabilidad con el punto de pivote. [55]
El mecanismo de relojería existente, el escape de verge , hacía que los péndulos oscilaran en arcos muy amplios de unos 100°. [56] Huygens demostró que esto era una fuente de inexactitud, ya que hacía que el período variara con los cambios de amplitud causados por pequeñas variaciones inevitables en la fuerza motriz del reloj. [57] Para hacer que su período fuera isócrono, Huygens montó guías metálicas con forma cicloidal junto a los pivotes de sus relojes, que restringían la cuerda de suspensión y obligaban al péndulo a seguir un arco cicloidal (véase péndulo cicloidal ). [58] Esta solución no resultó tan práctica como limitar simplemente la oscilación del péndulo a pequeños ángulos de unos pocos grados. La constatación de que solo las oscilaciones pequeñas eran isócronas motivó el desarrollo del escape de áncora alrededor de 1670, que redujo la oscilación del péndulo en los relojes a 4°–6°. [56] [59] Este se convirtió en el escape estándar utilizado en los relojes de péndulo.
1721: Péndulos con compensación de temperatura

Durante los siglos XVIII y XIX, el papel del reloj de péndulo como el cronómetro más preciso motivó mucha investigación práctica para mejorar los péndulos. Se descubrió que una fuente importante de error era que la varilla del péndulo se expandía y contraía con los cambios en la temperatura ambiente, modificando el período de oscilación. [9] [60] Esto se solucionó con la invención de péndulos con compensación de temperatura, el péndulo de mercurio en 1721 [61] y el péndulo de rejilla en 1726, reduciendo los errores en los relojes de péndulo de precisión a unos pocos segundos por semana. [58]
La precisión de las mediciones de gravedad realizadas con péndulos estaba limitada por la dificultad de encontrar la ubicación de su centro de oscilación . Huygens había descubierto en 1673 que un péndulo tiene el mismo período cuando está colgado de su centro de oscilación que cuando está colgado de su pivote, [18] y la distancia entre los dos puntos era igual a la longitud de un péndulo de gravedad simple del mismo período. [15] En 1818, el capitán británico Henry Kater inventó el péndulo de Kater reversible [62] que utilizaba este principio, haciendo posible mediciones muy precisas de la gravedad. Durante el siglo siguiente, el péndulo reversible fue el método estándar para medir la aceleración gravitatoria absoluta.
1851: El péndulo de Foucault
En 1851, Jean Bernard Léon Foucault demostró que el plano de oscilación de un péndulo, como un giroscopio , tiende a permanecer constante independientemente del movimiento del pivote, y que esto podría usarse para demostrar la rotación de la Tierra . Suspendió un péndulo libre para oscilar en dos dimensiones (más tarde llamado péndulo de Foucault ) de la cúpula del Panteón de París. La longitud de la cuerda era de 67 m (220 pies). Una vez que el péndulo se puso en movimiento, se observó que el plano de oscilación precesaba o rotaba 360° en el sentido de las agujas del reloj en aproximadamente 32 horas. [63] Esta fue la primera demostración de la rotación de la Tierra que no dependía de observaciones celestiales, [64] y estalló una "manía del péndulo", ya que los péndulos de Foucault se exhibieron en muchas ciudades y atrajeron grandes multitudes. [65] [66]
1930: Disminución del uso
Alrededor de 1900, se empezaron a utilizar materiales de baja expansión térmica para las varillas de péndulo en los relojes de máxima precisión y otros instrumentos, primero invar , una aleación de acero al níquel, y más tarde cuarzo fundido , que hizo que la compensación de temperatura fuera trivial. [67] Los péndulos de precisión se alojaban en tanques de baja presión, que mantenían la presión del aire constante para evitar cambios en el período debido a cambios en la flotabilidad del péndulo debido al cambio de presión atmosférica . [67] Los mejores relojes de péndulo alcanzaron una precisión de alrededor de un segundo por año. [68] [69]
La precisión del cronometraje del péndulo fue superada por el oscilador de cristal de cuarzo , inventado en 1921, y los relojes de cuarzo , inventados en 1927, reemplazaron a los relojes de péndulo como los mejores cronometradores del mundo. [2] Los relojes de péndulo se utilizaron como estándares de tiempo hasta la Segunda Guerra Mundial, aunque el Servicio de Hora Francés continuó usándolos en su conjunto de estándares de tiempo oficial hasta 1954. [70] Los gravímetros de péndulo fueron reemplazados por gravímetros de "caída libre" en la década de 1950, [71] pero los instrumentos de péndulo continuaron siendo utilizados hasta la década de 1970.
Uso para medir el tiempo
Durante 300 años, desde su descubrimiento alrededor de 1582 hasta el desarrollo del reloj de cuarzo en la década de 1930, el péndulo fue el estándar mundial para medir el tiempo con precisión. [2] [72] Además de los péndulos de reloj, los péndulos de segundos de oscilación libre se usaron ampliamente como cronómetros de precisión en experimentos científicos en los siglos XVII y XVIII. Los péndulos requieren una gran estabilidad mecánica: un cambio de longitud de solo 0,02%, 0,2 mm en un péndulo de reloj de pie, causará un error de un minuto por semana. [73]
Péndulos de reloj
Los péndulos de los relojes (véase el ejemplo de la derecha) suelen estar formados por un peso o pesa (b) suspendido de una varilla de madera o metal (a) . [9] [74] Para reducir la resistencia del aire (que explica la mayor parte de la pérdida de energía en los relojes de precisión) [75] la pesa es tradicionalmente un disco liso con una sección transversal en forma de lente, aunque en los relojes antiguos a menudo tenía tallas o decoraciones específicas del tipo de reloj. En los relojes de calidad, la pesa se hace tan pesada como la suspensión puede soportar y el movimiento puede impulsar, ya que esto mejora la regulación del reloj (véase Precisión a continuación). Un peso común para las pesas de péndulo de segundos es de 15 libras (6,8 kg). [76] En lugar de colgar de un pivote, los péndulos de los relojes suelen estar sostenidos por un resorte corto y recto (d) de cinta metálica flexible. Esto evita la fricción y el "juego" causados por un pivote, y la ligera fuerza de flexión del resorte simplemente se suma a la fuerza de restauración del péndulo . Los relojes de mayor precisión tienen pivotes de hojas de "cuchillo" que descansan sobre placas de ágata. Los impulsos para mantener el péndulo oscilando son proporcionados por un brazo que cuelga detrás del péndulo llamado muleta , (e) , que termina en una horquilla , (f) cuyas puntas abrazan la varilla del péndulo. La muleta es empujada hacia adelante y hacia atrás por el escape del reloj , (g,h) .
Cada vez que el péndulo oscila hasta su posición central, libera un diente de la rueda de escape (g) . La fuerza del resorte principal del reloj o de un peso impulsor que cuelga de una polea, transmitida a través del tren de engranajes del reloj , hace que la rueda gire y un diente presiona contra una de las paletas (h) , lo que le da al péndulo un pequeño empujón. Las ruedas del reloj, engranadas con la rueda de escape, avanzan una cantidad fija con cada oscilación del péndulo, avanzando las manecillas del reloj a un ritmo constante.
El péndulo siempre tiene un medio para ajustar el período, generalmente mediante una tuerca de ajuste (c) debajo de la pesa que lo mueve hacia arriba o hacia abajo en la varilla. [9] [77] Al mover la pesa hacia arriba, se reduce la longitud del péndulo, lo que hace que el péndulo oscile más rápido y el reloj gane tiempo. Algunos relojes de precisión tienen un pequeño peso de ajuste auxiliar en un eje roscado en la pesa, para permitir un ajuste más preciso. Algunos relojes de torre y relojes de precisión utilizan una bandeja unida cerca del punto medio de la varilla del péndulo, a la que se pueden agregar o quitar pequeños pesos. Esto cambia efectivamente el centro de oscilación y permite ajustar la velocidad sin detener el reloj. [78] [79]
El péndulo debe estar suspendido de un soporte rígido. [9] [80] Durante el funcionamiento, cualquier elasticidad permitirá pequeños movimientos de balanceo imperceptibles del soporte, lo que altera el período del reloj y da como resultado un error. Los relojes de péndulo deben estar fijados firmemente a una pared resistente.
La longitud de péndulo más común en los relojes de calidad, que siempre se utiliza en los relojes de pie , es el péndulo de segundos , de aproximadamente 1 metro (39 pulgadas) de largo. En los relojes de repisa , se utilizan péndulos de medio segundo, de 25 cm (9,8 pulgadas) de largo, o más cortos. Solo unos pocos relojes de torre grandes utilizan péndulos más largos, el péndulo de 1,5 segundos, de 2,25 m (7,4 pies) de largo, u ocasionalmente el péndulo de dos segundos, de 4 m (13 pies) [9] [81] que se utiliza en el Big Ben . [82]
Compensación de temperatura

La mayor fuente de error en los primeros péndulos eran los ligeros cambios en la longitud debido a la expansión y contracción térmica de la varilla del péndulo con los cambios en la temperatura ambiente. [83] Esto se descubrió cuando la gente notó que los relojes de péndulo funcionaban más lento en verano, hasta un minuto por semana [60] [84] (uno de los primeros fue Godefroy Wendelin , como informó Huygens en 1658). [85] La expansión térmica de las varillas del péndulo fue estudiada por primera vez por Jean Picard en 1669. [86] [87] Un péndulo con una varilla de acero se expandirá aproximadamente 11,3 partes por millón (ppm) con cada aumento de grado Celsius, lo que hace que pierda aproximadamente 0,27 segundos por día por cada aumento de grado Celsius en la temperatura, o 9 segundos por día para un cambio de 33 °C (59 °F). Las varillas de madera se dilatan menos, perdiendo sólo unos 6 segundos al día por cada 33 °C (59 °F) de variación, por lo que los relojes de calidad solían tener varillas de péndulo de madera. La madera debía estar barnizada para evitar la entrada de vapor de agua, ya que los cambios de humedad también afectaban a la longitud.
Péndulo de mercurio
El primer dispositivo para compensar este error fue el péndulo de mercurio, inventado por George Graham [61] en 1721. [9] [84] El mercurio, un metal líquido, se expande en volumen con la temperatura. En un péndulo de mercurio, el peso del péndulo (pesa) es un recipiente de mercurio. Con un aumento de temperatura, la varilla del péndulo se hace más larga, pero el mercurio también se expande y su nivel de superficie sube ligeramente en el recipiente, moviendo su centro de masa más cerca del pivote del péndulo. Al usar la altura correcta de mercurio en el recipiente, estos dos efectos se cancelarán, dejando el centro de masa del péndulo, y su período, sin cambios con la temperatura. Su principal desventaja era que cuando la temperatura cambiaba, la varilla alcanzaba la nueva temperatura rápidamente, pero la masa de mercurio podía tardar un día o dos en alcanzar la nueva temperatura, lo que hacía que la velocidad se desviara durante ese tiempo. [88] Para mejorar la acomodación térmica, a menudo se usaban varios recipientes delgados, hechos de metal. Los péndulos de mercurio fueron el estándar utilizado en los relojes reguladores de precisión hasta el siglo XX. [89]
Péndulo de parrilla
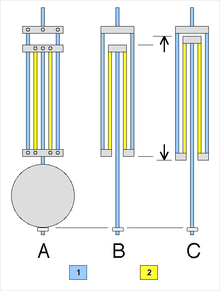
- esquema exterior
- temperatura normal
- temperatura más alta
El péndulo compensado más utilizado fue el péndulo de rejilla , inventado en 1726 por John Harrison . [9] [84] [88] Este consiste en varillas alternadas de dos metales diferentes, uno con menor expansión térmica ( CTE ), acero , y otro con mayor expansión térmica, zinc o latón . Las varillas están conectadas por un marco, como se muestra en el dibujo de la derecha, de modo que un aumento en la longitud de las varillas de zinc empuja la plomada hacia arriba, acortando el péndulo. Con un aumento de temperatura, las varillas de acero de baja expansión hacen que el péndulo sea más largo, mientras que las varillas de zinc de alta expansión lo hacen más corto. Al hacer las varillas de las longitudes correctas, la mayor expansión del zinc anula la expansión de las varillas de acero que tienen una mayor longitud combinada, y el péndulo permanece con la misma longitud con la temperatura.
Los péndulos de rejilla de acero y zinc están hechos con 5 varillas, pero la expansión térmica del latón es más cercana a la del acero, por lo que las rejillas de latón y acero generalmente requieren 9 varillas. Los péndulos de rejilla se ajustan a los cambios de temperatura más rápido que los péndulos de mercurio, pero los científicos descubrieron que la fricción de las varillas que se deslizaban en sus agujeros en el marco causaba que los péndulos de rejilla se ajustaran en una serie de pequeños saltos. [88] En los relojes de alta precisión, esto causaba que la velocidad del reloj cambiara repentinamente con cada salto. Más tarde se descubrió que el zinc está sujeto a deslizamiento . Por estas razones, se utilizaron péndulos de mercurio en los relojes de mayor precisión, pero las rejillas se usaron en relojes reguladores de calidad.
Los péndulos de rejilla se asociaron tanto con la buena calidad que, hasta el día de hoy, muchos péndulos de reloj comunes tienen rejillas decorativas "falsas" que en realidad no tienen ninguna función de compensación de temperatura.
Invar y cuarzo fundido
Alrededor de 1900, se desarrollaron materiales de baja expansión térmica que podían usarse como varillas de péndulo para hacer innecesaria la compensación de temperatura elaborada. [9] [84] Estos solo se usaron en algunos de los relojes de mayor precisión antes de que el péndulo se volviera obsoleto como estándar de tiempo. En 1896, Charles Édouard Guillaume inventó la aleación de acero al níquel Invar . Esta tiene un CTE de alrededor de 0,9 ppm /°C (0,5 ppm/°F ), lo que da como resultado errores de temperatura del péndulo por encima de los 22 °C (71 °F) de solo 1,3 segundos por día, y este error residual podría compensarse a cero con unos pocos centímetros de aluminio debajo del cuerpo del péndulo [2] [88] (esto se puede ver en la imagen del reloj Riefler anterior). Los péndulos de invar se utilizaron por primera vez en 1898 en el reloj regulador Riefler [90] que logró una precisión de 15 milisegundos por día. Se utilizaron resortes de suspensión de Elinvar para eliminar la variación de temperatura de la fuerza de restauración del resorte en el péndulo. Más tarde se utilizó cuarzo fundido que tenía un CTE incluso más bajo. Estos materiales son la opción para los péndulos modernos de alta precisión. [91]
Presión atmosférica
El efecto del aire circundante sobre un péndulo en movimiento es complejo y requiere mecánica de fluidos para calcularlo con precisión, pero para la mayoría de los propósitos su influencia en el período se puede explicar por tres efectos: [67] [92]
- Según el principio de Arquímedes, el peso efectivo del péndulo se reduce por la flotabilidad del aire que desplaza, mientras que la masa ( inercia ) permanece igual, lo que reduce la aceleración del péndulo durante su oscilación y aumenta el período. Esto depende de la presión del aire y de la densidad del péndulo, pero no de su forma.
- El péndulo lleva consigo una cantidad de aire mientras oscila y la masa de este aire aumenta la inercia del péndulo, reduciendo nuevamente la aceleración y aumentando el período. Esto depende tanto de su densidad como de su forma.
- La resistencia del aire viscoso reduce la velocidad del péndulo, lo que tiene un efecto insignificante en el período, pero disipa energía y reduce la amplitud. Esto reduce el factor Q del péndulo , lo que requiere una fuerza impulsora más fuerte del mecanismo del reloj para mantenerlo en movimiento, lo que provoca una mayor perturbación en el período.
Los aumentos en la presión barométrica aumentan ligeramente el período de un péndulo debido a los dos primeros efectos, en aproximadamente 0,11 segundos por día por kilopascal (0,37 segundos por día por pulgada de mercurio ; 0,015 segundos por día por torr ). [67] Los investigadores que usaban péndulos para medir la aceleración de la gravedad tuvieron que corregir el período para la presión del aire a la altitud de medición, calculando el período equivalente de un péndulo oscilando en el vacío. Un reloj de péndulo fue operado por primera vez en un tanque de presión constante por Friedrich Tiede en 1865 en el Observatorio de Berlín , [93] [94] y para 1900 los relojes de mayor precisión se montaron en tanques que se mantenían a una presión constante para eliminar los cambios en la presión atmosférica. Alternativamente, en algunos un pequeño mecanismo de barómetro aneroide unido al péndulo compensaba este efecto.
Gravedad
Los péndulos se ven afectados por los cambios en la aceleración gravitacional, que varía hasta en un 0,5 % en diferentes lugares de la Tierra, por lo que los relojes de péndulo de precisión deben recalibrarse después de un traslado. Incluso mover un reloj de péndulo a la cima de un edificio alto puede hacer que pierda tiempo medible debido a la reducción de la gravedad.
Precisión de los péndulos como cronometradores
Los elementos de cronometraje en todos los relojes, que incluyen péndulos, ruedas de equilibrio , los cristales de cuarzo utilizados en los relojes de cuarzo e incluso los átomos vibrantes en los relojes atómicos , se denominan en física osciladores armónicos . La razón por la que se utilizan osciladores armónicos en los relojes es que vibran u oscilan a una frecuencia o período de resonancia específico y se resisten a oscilar a otras velocidades. Sin embargo, la frecuencia de resonancia no es infinitamente "aguda". Alrededor de la frecuencia de resonancia hay una estrecha banda natural de frecuencias (o períodos), llamada ancho de banda o ancho de banda de resonancia , donde oscilará el oscilador armónico. [95] [96] En un reloj, la frecuencia real del péndulo puede variar aleatoriamente dentro de este ancho de resonancia en respuesta a perturbaciones, pero a frecuencias fuera de esta banda, el reloj no funcionará en absoluto. El ancho de resonancia está determinado por la amortiguación , la pérdida de energía por fricción por oscilación del péndulo.
Qfactor

La medida de la resistencia de un oscilador armónico a las perturbaciones de su período de oscilación es un parámetro adimensional llamado factor Q igual a la frecuencia de resonancia dividida por el ancho de resonancia . [96] [97] Cuanto mayor sea el Q , menor será el ancho de resonancia y más constante será la frecuencia o el período del oscilador para una perturbación dada. [98] El recíproco del Q es aproximadamente proporcional a la precisión límite alcanzable por un oscilador armónico como estándar de tiempo. [99]
La Q está relacionada con el tiempo que tardan las oscilaciones de un oscilador en extinguirse. La Q de un péndulo se puede medir contando la cantidad de oscilaciones que tarda la amplitud de oscilación del péndulo en disminuir a 1/ e = 36,8 % de su oscilación inicial, y multiplicando por 'π .
En un reloj, el péndulo debe recibir empujes del movimiento del reloj para mantenerlo oscilando, para reemplazar la energía que el péndulo pierde por fricción. Estos empujes, aplicados por un mecanismo llamado escape , son la principal fuente de perturbación del movimiento del péndulo. La Q es igual a 2 π por la energía almacenada en el péndulo, dividida por la energía perdida por fricción durante cada período de oscilación, que es la misma que la energía agregada por el escape en cada período. Se puede ver que cuanto menor es la fracción de la energía del péndulo que se pierde por fricción, menos energía se necesita agregar, cuanto menor es la perturbación del escape, más "independiente" es el péndulo del mecanismo del reloj y más constante es su período. La Q de un péndulo viene dada por: donde M es la masa del péndulo, ω = 2 π / T es la frecuencia radiana de oscilación del péndulo y Γ es la fuerza de amortiguación por fricción en el péndulo por unidad de velocidad.
ω está determinado por el período del péndulo y M está limitado por la capacidad de carga y la rigidez de la suspensión. Por lo tanto, la Q de los péndulos de reloj aumenta al minimizar las pérdidas por fricción (Γ). Los péndulos de precisión están suspendidos sobre pivotes de baja fricción que consisten en bordes de "cuchillo" con forma triangular que descansan sobre placas de ágata. Alrededor del 99% de la pérdida de energía en un péndulo que oscila libremente se debe a la fricción del aire, por lo que montar un péndulo en un tanque de vacío puede aumentar la Q y, por lo tanto, la precisión, en un factor de 100. [100]
El Q de los péndulos varía desde varios miles en un reloj ordinario hasta varios cientos de miles para péndulos reguladores de precisión que oscilan en el vacío. [101] Un reloj de péndulo doméstico de calidad puede tener un Q de 10.000 y una precisión de 10 segundos al mes. El reloj de péndulo comercialmente producido más preciso fue el reloj de péndulo libre Shortt-Synchronome , inventado en 1921. [2] [68] [102] [103] [104] Su péndulo maestro Invar que oscilaba en un tanque de vacío tenía un Q de 110.000 [101] y una tasa de error de alrededor de un segundo al año. [68]
Su Q de 10 3 –10 5 es una de las razones por las que los péndulos son cronometradores más precisos que los volantes de los relojes, con Q alrededor de 100–300, pero menos precisos que los cristales de cuarzo en los relojes de cuarzo , con Q de 10 5 –10 6. [2] [101]
Escape
Los péndulos (a diferencia, por ejemplo, de los cristales de cuarzo) tienen una Q lo suficientemente baja como para que la perturbación causada por los impulsos que los mantienen en movimiento sea generalmente el factor limitante de su precisión en el cronometraje. Por lo tanto, el diseño del escape , el mecanismo que proporciona estos impulsos, tiene un gran efecto en la precisión de un péndulo de reloj. Si los impulsos dados al péndulo por el escape en cada oscilación pudieran ser exactamente idénticos, la respuesta del péndulo sería idéntica y su período sería constante. Sin embargo, esto no es posible; las inevitables fluctuaciones aleatorias en la fuerza debido a la fricción de las paletas del reloj, las variaciones de lubricación y los cambios en el par proporcionado por la fuente de energía del reloj a medida que se agota, significan que la fuerza del impulso aplicado por el escape varía.
Si estas variaciones en la fuerza del escape provocan cambios en la amplitud de oscilación del péndulo, esto provocará ligeros cambios correspondientes en el período, ya que (como se explicó anteriormente) un péndulo con una oscilación finita no es completamente isócrono. Por lo tanto, el objetivo del diseño tradicional de escapes es aplicar la fuerza con el perfil adecuado y en el punto correcto del ciclo del péndulo, de modo que las variaciones de fuerza no tengan efecto en la amplitud del péndulo. Esto se denomina escape isócrono .
La condición del aire
Los relojeros sabían desde hace siglos que el efecto perturbador de la fuerza motriz del escape sobre el período de un péndulo es mínimo si se da como un impulso corto cuando el péndulo pasa por su posición de equilibrio inferior . [2] Si el impulso se produce antes de que el péndulo llegue al fondo, durante la oscilación descendente, tendrá el efecto de acortar el período natural del péndulo, por lo que un aumento en la fuerza motriz disminuirá el período. Si el impulso se produce después de que el péndulo llegue al fondo, durante la oscilación ascendente, alargará el período, por lo que un aumento en la fuerza motriz aumentará el período del péndulo. En 1826, el astrónomo británico George Airy demostró esto; específicamente, demostró que si un péndulo es impulsado por un impulso que es simétrico respecto de su posición de equilibrio inferior, el período del péndulo no se verá afectado por los cambios en la fuerza motriz. [105] Los escapes más precisos, como el deadbeat , satisfacen aproximadamente esta condición. [106]
Medición de la gravedad
La presencia de la aceleración de la gravedad g en la ecuación de periodicidad (1) para un péndulo significa que la aceleración gravitacional local de la Tierra se puede calcular a partir del período de un péndulo. Por lo tanto, un péndulo se puede utilizar como un gravímetro para medir la gravedad local , que varía en más del 0,5% a lo largo de la superficie de la Tierra. [107] [Nota 2] El péndulo de un reloj se ve perturbado por los empujones que recibe del movimiento del reloj, por lo que se utilizaron péndulos de oscilación libre, que fueron los instrumentos estándar de gravimetría hasta la década de 1930.
La diferencia entre los péndulos de los relojes y los péndulos gravímetros es que para medir la gravedad, se debe medir la longitud del péndulo, así como su período. El período de los péndulos que oscilan libremente se puede determinar con gran precisión comparando su oscilación con la de un reloj de precisión que se hubiera ajustado para que marcara la hora correcta según el paso de las estrellas por encima de él. En las primeras mediciones, se suspendía un peso en una cuerda delante del péndulo del reloj y se ajustaba su longitud hasta que los dos péndulos oscilaran en sincronía exacta. Luego se medía la longitud de la cuerda. A partir de la longitud y el período, se podía calcular g a partir de la ecuación (1).
El péndulo de segundos
El péndulo de segundos , un péndulo con un período de dos segundos, por lo que cada oscilación dura un segundo, se utilizó ampliamente para medir la gravedad, porque su período se podía medir fácilmente comparándolo con los relojes con regulador de precisión , que todos tenían péndulos de segundos. A fines del siglo XVII, la longitud del péndulo de segundos se convirtió en la medida estándar de la fuerza de la aceleración gravitacional en un lugar. En 1700, su longitud se había medido con precisión submilimétrica en varias ciudades de Europa. Para un péndulo de segundos, g es proporcional a su longitud:
Observaciones tempranas
- 1620 : el científico británico Francis Bacon fue uno de los primeros en proponer el uso de un péndulo para medir la gravedad, sugiriendo llevarlo a una montaña para ver si la gravedad varía con la altitud. [108]
- 1644 : Incluso antes de que existiera el reloj de péndulo, el sacerdote francés Marin Mersenne determinó por primera vez que la longitud del segundero era de 39,1 pulgadas (990 mm), comparando la oscilación de un péndulo con el tiempo que tardaba un peso en caer una distancia determinada. También fue el primero en descubrir la dependencia del período con la amplitud de la oscilación.
- 1669 : Jean Picard determinó la longitud del péndulo de segundos en París, utilizando una bola de cobre de 1 pulgada (25 mm) suspendida por una fibra de aloe, obteniendo 39,09 pulgadas (993 mm). [109] También realizó los primeros experimentos sobre la expansión y contracción térmica de las varillas del péndulo con la temperatura.
- 1672 : La primera observación de que la gravedad variaba en diferentes puntos de la Tierra fue realizada en 1672 por Jean Richer , quien llevó un reloj de péndulo a Cayena , Guayana Francesa y descubrió que perdía 2+1 ⁄ 2 minutos por día; su péndulo de segundos tuvo que ser acortado en 1+1 ⁄ 4 líneas (2,6 mm) más cortas que en París, para mantener la hora correcta. [110] [111] En 1687, Isaac Newton en Principia Mathematica demostró que esto se debía a que la Tierra tenía una forma ligeramente achatada (aplanada en los polos) causada por la fuerza centrífuga de su rotación. En latitudes más altas, la superficie estaba más cerca del centro de la Tierra, por lo que la gravedad aumentaba con la latitud. [111] A partir de este momento, se empezaron a llevar péndulos a tierras lejanas para medir la gravedad, y se compilaron tablas de la longitud del péndulo de segundos en diferentes lugares de la Tierra. En 1743, Alexis Claude Clairaut creó el primer modelo hidrostático de la Tierra, el teorema de Clairaut , [109] que permitió calcular la elipticidad de la Tierra a partir de mediciones de la gravedad. Progresivamente, le siguieron modelos más precisos de la forma de la Tierra.
- 1687 : Newton experimentó con péndulos (descritos en Principia ) y descubrió que péndulos de igual longitud hechos de materiales diferentes tenían el mismo período, lo que demostraba que la fuerza gravitatoria sobre sustancias diferentes era exactamente proporcional a su masa (inercia). Este principio, llamado principio de equivalencia , confirmado con mayor precisión en experimentos posteriores, se convirtió en la base sobre la que Albert Einstein basó su teoría general de la relatividad .

- 1737 : El matemático francés Pierre Bouguer realizó una serie sofisticada de observaciones de péndulo en las montañas de los Andes , Perú. [112] Utilizó un péndulo de cobre en forma de cono de doble punta suspendido por un hilo; el péndulo se podía invertir para eliminar los efectos de la densidad no uniforme. Calculó la longitud hasta el centro de oscilación del hilo y el péndulo combinados, en lugar de utilizar el centro del péndulo. Corrigió la expansión térmica de la varilla de medición y la presión barométrica, dando sus resultados para un péndulo oscilando en el vacío. Bouguer hizo oscilar el mismo péndulo a tres elevaciones diferentes, desde el nivel del mar hasta la cima del alto altiplano peruano . La gravedad debería caer con el cuadrado inverso de la distancia desde el centro de la Tierra. Bouguer descubrió que caía más lentamente y atribuyó correctamente la gravedad "extra" al campo gravitacional de la enorme meseta peruana. A partir de la densidad de muestras de rocas calculó una estimación del efecto del altiplano sobre el péndulo, y comparándolo con la gravedad de la Tierra pudo hacer la primera estimación aproximada de la densidad de la Tierra .
- 1747 : Daniel Bernoulli demostró cómo corregir el alargamiento del período debido a un ángulo finito de oscilación θ 0 utilizando la corrección de primer orden θ 0 2 /16, dando como resultado el período de un péndulo con una oscilación extremadamente pequeña. [112]
- 1792 : Para definir un patrón de longitud del péndulo para su uso con el nuevo sistema métrico , en 1792 Jean-Charles de Borda y Jean-Dominique Cassini realizaron una medición precisa del péndulo de segundos en París. Utilizaron un péndulo de 1+Bola de platino de 1 ⁄ 2 pulgada (14 mm) [ aclaración necesaria ] suspendida de un alambre de hierro de 12 pies (3,7 m). Su principal innovación fue una técnica llamada " método de las coincidencias ", que permitía comparar el período de los péndulos con gran precisión. (Bouguer también había utilizado este método). Se cronometró el intervalo de tiempo Δ t entre los instantes recurrentes en que los dos péndulos oscilaron en sincronismo. A partir de esto, se pudo calcular la diferencia entre los períodos de los péndulos, T 1 y T 2 :
- 1821 : Francesco Carlini hizo observaciones con un péndulo en la cima del monte Cenis, en Italia, a partir de las cuales, utilizando métodos similares a los de Bouguer, calculó la densidad de la Tierra. [113] Comparó sus mediciones con una estimación de la gravedad en su ubicación asumiendo que la montaña no estaba allí, calculada a partir de mediciones previas con un péndulo cercano al nivel del mar. Sus mediciones mostraron un "exceso" de gravedad, que atribuyó al efecto de la montaña. Modelando la montaña como un segmento de una esfera de 11 millas (18 km) de diámetro y 1 milla (1,6 km) de altura, a partir de muestras de roca calculó su campo gravitatorio y estimó la densidad de la Tierra en 4,39 veces la del agua. Los cálculos posteriores de otros dieron valores de 4,77 y 4,95, lo que ilustra las incertidumbres de estos métodos geográficos.
El péndulo de Kater
 |  |

La precisión de las primeras mediciones de gravedad mencionadas anteriormente estaba limitada por la dificultad de medir la longitud del péndulo, L. L era la longitud de un péndulo de gravedad simple idealizado (descrito en la parte superior), que tiene toda su masa concentrada en un punto al final de la cuerda. En 1673, Huygens había demostrado que el período de un péndulo de barra rígida (llamado péndulo compuesto ) era igual al período de un péndulo simple con una longitud igual a la distancia entre el punto de pivote y un punto llamado centro de oscilación , ubicado debajo del centro de gravedad , que depende de la distribución de masa a lo largo del péndulo. Pero no había una forma precisa de determinar el centro de oscilación en un péndulo real. El descubrimiento de Huygens a veces se conoce como la ley de Huygens del péndulo (cicloidal) . [114]
Para solucionar este problema, los primeros investigadores que se mencionaron anteriormente se aproximaron lo más posible a un péndulo simple ideal utilizando una esfera de metal suspendida de un cable o cuerda liviana. Si el cable era lo suficientemente liviano, el centro de oscilación estaba cerca del centro de gravedad de la bola, en su centro geométrico. Este tipo de péndulo de "bola y cable" no era muy preciso, porque no oscilaba como un cuerpo rígido y la elasticidad del cable hacía que su longitud cambiara ligeramente a medida que oscilaba el péndulo.
Sin embargo, Huygens también había demostrado que en cualquier péndulo, el punto de pivote y el centro de oscilación eran intercambiables. [18] Es decir, si un péndulo se girara y se colgara de su centro de oscilación, tendría el mismo período que en la posición anterior, y el antiguo punto de pivote sería el nuevo centro de oscilación.
El físico y capitán del ejército británico Henry Kater se dio cuenta en 1817 de que el principio de Huygens podía usarse para encontrar la longitud de un péndulo simple con el mismo período que un péndulo real. [62] Si se construía un péndulo con un segundo punto de pivote ajustable cerca de la parte inferior para poder colgarlo boca abajo, y el segundo pivote se ajustaba hasta que los períodos cuando se colgaba de ambos pivotes fueran los mismos, el segundo pivote estaría en el centro de oscilación, y la distancia entre los dos pivotes sería la longitud L de un péndulo simple con el mismo período.
Kater construyó un péndulo reversible ( ver dibujo ) que consistía en una barra de latón con dos pivotes opuestos hechos de hojas cortas triangulares en forma de "cuchillo" (a) cerca de cada extremo. Podía oscilar desde cualquiera de los pivotes, con las hojas del cuchillo apoyadas sobre placas de ágata. En lugar de hacer que un pivote fuera ajustable, colocó los pivotes a un metro de distancia y en su lugar ajustó los períodos con un peso móvil en la varilla del péndulo (b, c) . En funcionamiento, el péndulo se cuelga frente a un reloj de precisión y se cronometra el período, luego se le da la vuelta y se vuelve a cronometrar el período. El peso se ajusta con el tornillo de ajuste hasta que los períodos sean iguales. Luego, al poner este período y la distancia entre los pivotes en la ecuación (1), se obtiene la aceleración gravitacional g con mucha precisión.
Kater cronometró la oscilación de su péndulo utilizando el " método de las coincidencias " y midió la distancia entre los dos pivotes con un micrómetro. Después de aplicar correcciones para la amplitud finita de oscilación, la flotabilidad del péndulo, la presión barométrica y la altitud, y la temperatura, obtuvo un valor de 39,13929 pulgadas para el péndulo de segundos en Londres, en el vacío, al nivel del mar, a 62 °F. La mayor variación con respecto a la media de sus 12 observaciones fue de 0,00028 pulgadas [115] , lo que representa una precisión de la medición de la gravedad de 7×10 −6 (7 mGal o 70 μm/s 2 ). La medida de Kater se utilizó como estándar oficial de longitud de Gran Bretaña (véase más abajo) desde 1824 hasta 1855.
Los péndulos reversibles (conocidos técnicamente como péndulos "convertibles") que emplean el principio de Kater se utilizaron para mediciones de gravedad absoluta hasta la década de 1930.
Gravímetros de péndulo posteriores
La mayor precisión que permitió el péndulo de Kater ayudó a que la gravimetría se convirtiera en una parte estándar de la geodesia . Dado que era necesaria la ubicación exacta (latitud y longitud) de la "estación" donde se realizaba la medición de la gravedad, las mediciones de gravedad se convirtieron en parte de la topografía y se tomaron péndulos en los grandes estudios geodésicos del siglo XVIII, en particular en el Gran Estudio Trigonométrico de la India.

- Péndulos invariables: Kater introdujo la idea de las mediciones de gravedad relativa , para complementar las mediciones absolutas realizadas con un péndulo de Kater. [116] Comparar la gravedad en dos puntos diferentes era un proceso más fácil que medirla de forma absoluta con el método de Kater. Todo lo que era necesario era cronometrar el período de un péndulo ordinario (de un solo pivote) en el primer punto, luego transportar el péndulo al otro punto y cronometrar su período allí. Como la longitud del péndulo era constante, a partir de (1) la relación de las aceleraciones gravitacionales era igual a la inversa de la relación de los períodos al cuadrado, y no eran necesarias mediciones de longitud precisas. De modo que una vez que se había medido la gravedad de forma absoluta en alguna estación central, mediante el método de Kater u otro método preciso, la gravedad en otros puntos podía determinarse haciendo oscilar péndulos en la estación central y luego llevándolos a la otra ubicación y cronometrando su oscilación allí. Kater fabricó un conjunto de péndulos "invariables", con un solo pivote en forma de cuchillo, que fueron llevados a muchos países después de oscilar por primera vez en una estación central en el Observatorio de Kew , en el Reino Unido.
- Experimentos de Airy en la mina de carbón : a partir de 1826, utilizando métodos similares a los de Bouguer, el astrónomo británico George Airy intentó determinar la densidad de la Tierra mediante mediciones de gravedad con péndulo en la parte superior e inferior de una mina de carbón. [117] [118] La fuerza gravitatoria debajo de la superficie de la Tierra disminuye en lugar de aumentar con la profundidad, porque según la ley de Gauss, la masa de la capa esférica de corteza sobre el punto subterráneo no contribuye a la gravedad. El experimento de 1826 fue abortado por la inundación de la mina, pero en 1854 realizó un experimento mejorado en la mina de carbón de Harton, utilizando péndulos de segundos que oscilaban sobre placas de ágata, cronometrados por cronómetros de precisión sincronizados por un circuito eléctrico. Descubrió que el péndulo inferior era más lento en 2,24 segundos por día. Esto significaba que la aceleración gravitatoria en el fondo de la mina, a 1250 pies por debajo de la superficie, era 1/14.000 menor de lo que debería haber sido según la ley del cuadrado inverso; es decir, la atracción de la capa esférica era 1/14.000 de la atracción de la Tierra. A partir de muestras de roca superficial, estimó la masa de la capa esférica de corteza y, a partir de esto, estimó que la densidad de la Tierra era 6,565 veces la del agua. Von Sterneck intentó repetir el experimento en 1882, pero obtuvo resultados inconsistentes.

- Péndulo de Repsold-Bessel: Hacer oscilar repetidamente el péndulo de Kater y ajustar los pesos hasta que los períodos fueran iguales requería mucho tiempo y era propenso a errores. Friedrich Bessel demostró en 1835 que esto era innecesario. [119] Mientras los períodos estuvieran próximos entre sí, la gravedad podía calcularse a partir de los dos períodos y el centro de gravedad del péndulo. [120] Por lo tanto, el péndulo reversible no necesitaba ser ajustable, podía ser simplemente una barra con dos pivotes. Bessel también demostró que si el péndulo se hacía simétrico en forma respecto a su centro, pero se le aplicaba un peso interno en un extremo, los errores debidos a la resistencia del aire se anularían. Además, se podía anular otro error debido al diámetro finito de los bordes de la cuchilla si se intercambiaban entre mediciones. Bessel no construyó un péndulo de este tipo, pero en 1864 Adolf Repsold, bajo contrato con la Comisión Geodética Suiza, fabricó un péndulo de este tipo. El péndulo de Repsold medía unos 56 cm de largo y tenía un período de unos 3 ⁄ 4 de segundo. Fue utilizado ampliamente por las agencias geodésicas europeas y, junto con el péndulo de Kater, por el Survey of India. Charles Pierce y C. Defforges diseñaron péndulos similares de este tipo.

- Gravímetros de von Sterneck y Mendenhall: En 1887, el científico austrohúngaro Robert von Sterneck desarrolló un pequeño péndulo gravímetro montado en un tanque de vacío con control de temperatura para eliminar los efectos de la temperatura y la presión del aire. Utilizaba un "péndulo de medio segundo", con un período cercano a un segundo, de unos 25 cm de largo. El péndulo no era reversible, por lo que el instrumento se utilizó para mediciones de gravedad relativa, pero su pequeño tamaño lo hacía pequeño y portátil. El período del péndulo se obtenía reflejando la imagen de una chispa eléctrica creada por un cronómetro de precisión en un espejo montado en la parte superior de la varilla del péndulo. El instrumento de Von Sterneck, y un instrumento similar desarrollado por Thomas C. Mendenhall del United States Coast and Geodetic Survey en 1890, [121] se utilizaron ampliamente para estudios en la década de 1920.
- El péndulo de Mendenhall era en realidad un cronómetro más preciso que los relojes de mayor precisión de la época, y como el "mejor reloj del mundo" fue utilizado por Albert A. Michelson en sus mediciones de 1924 de la velocidad de la luz en el monte Wilson, California. [121]
- Gravímetros de doble péndulo: A partir de 1875, la creciente precisión de las mediciones con péndulo reveló otra fuente de error en los instrumentos existentes: la oscilación del péndulo causaba un ligero balanceo del trípode utilizado para sostener los péndulos portátiles, lo que introducía un error. En 1875, Charles S. Peirce calculó que las mediciones de la longitud del péndulo de segundos realizadas con el instrumento Repsold requerían una corrección de 0,2 mm debido a este error. [122] En 1880, C. Defforges utilizó un interferómetro de Michelson para medir dinámicamente el balanceo del soporte, y se añadieron interferómetros al aparato estándar de Mendenhall para calcular las correcciones del balanceo. [123] Un método para prevenir este error fue sugerido por primera vez en 1877 por Hervé Faye y defendido por Peirce, Cellérier y Furtwangler: montar dos péndulos idénticos en el mismo soporte, oscilando con la misma amplitud, 180° fuera de fase. El movimiento opuesto de los péndulos anularía cualquier fuerza lateral sobre el soporte. La idea fue rechazada debido a su complejidad, pero a principios del siglo XX se modificaron el dispositivo de Von Sterneck y otros instrumentos para hacer oscilar varios péndulos simultáneamente.

- Gravímetro del Golfo : Uno de los últimos y más precisos gravímetros de péndulo fue el aparato desarrollado en 1929 por la Gulf Research and Development Co. [124] [125] Utilizaba dos péndulos hechos de cuarzo fundido , cada uno de 10,7 pulgadas (270 mm) de longitud con un período de 0,89 segundos, que oscilaban sobre pivotes de pyrex con borde de cuchillo, 180° fuera de fase. Estaban montados en una cámara de vacío sellada permanentemente con temperatura y humedad controladas. Las cargas electrostáticas dispersas en los péndulos de cuarzo tenían que descargarse exponiéndolos a una sal radiactiva antes de su uso. El período se detectaba reflejando un haz de luz desde un espejo en la parte superior del péndulo, registrado por un registrador gráfico y comparado con un oscilador de cristal de precisión calibrado contra la señal horaria de radio WWV . Este instrumento tenía una precisión de (0,3–0,5)×10 −7 (30–50 microgals o 3–5 nm/s 2 ). [124] Se utilizó hasta la década de 1960.
Los gravímetros de péndulo relativos fueron reemplazados por el gravímetro de resorte de longitud cero LaCoste, más simple, inventado en 1934 por Lucien LaCoste . [121] Los gravímetros de péndulo absolutos (reversibles) fueron reemplazados en la década de 1950 por gravímetros de caída libre, en los que se permite que un peso caiga en un tanque de vacío y su aceleración se mide mediante un interferómetro óptico . [71]
Estándar de longitud
Como la aceleración de la gravedad es constante en un punto determinado de la Tierra, el período de un péndulo simple en un lugar determinado depende únicamente de su longitud. Además, la gravedad varía muy poco en diferentes lugares. Casi desde el descubrimiento del péndulo hasta principios del siglo XIX, esta propiedad llevó a los científicos a sugerir el uso de un péndulo de un período determinado como estándar de longitud .
Hasta el siglo XIX, los países basaban sus sistemas de medición de longitud en prototipos, patrones primarios de barras de metal , como la yarda estándar en Gran Bretaña que se guardaba en las Cámaras del Parlamento, y la toesa estándar en Francia, que se guardaba en París. Estos eran vulnerables a daños o destrucción con el paso de los años y, debido a la dificultad de comparar prototipos, la misma unidad a menudo tenía longitudes diferentes en ciudades distantes, lo que creaba oportunidades para el fraude. [126] Durante la Ilustración, los científicos abogaron por un estándar de longitud que se basara en alguna propiedad de la naturaleza que pudiera determinarse mediante la medición, creando un estándar universal e indestructible. El período de los péndulos podía medirse con mucha precisión cronometrándolos con relojes que se regulaban por las estrellas. Un estándar de péndulo equivalía a definir la unidad de longitud por la fuerza gravitatoria de la Tierra, a todos los efectos constante, y el segundo, que se definía por la velocidad de rotación de la Tierra , también constante. La idea era que cualquiera, en cualquier lugar de la Tierra, pudiera recrear el estándar construyendo un péndulo que oscilara con el período definido y midiendo su longitud.
Prácticamente todas las propuestas se basaban en el péndulo de segundos , en el que cada oscilación (medio período ) dura un segundo, es decir, aproximadamente un metro (39 pulgadas) de largo, porque a finales del siglo XVII se había convertido en un estándar para medir la gravedad (véase la sección anterior). En el siglo XVIII, su longitud ya se había medido con precisión submilimétrica en varias ciudades de Europa y de todo el mundo.
El atractivo inicial del estándar de longitud del péndulo fue que se creía (por los primeros científicos como Huygens y Wren) que la gravedad era constante sobre la superficie de la Tierra, por lo que un péndulo dado tenía el mismo período en cualquier punto de la Tierra. [126] Por lo tanto, la longitud del péndulo estándar podría medirse en cualquier ubicación y no estaría vinculada a ninguna nación o región determinada; sería un estándar mundial verdaderamente democrático. Aunque Richer descubrió en 1672 que la gravedad varía en diferentes puntos del globo, la idea de un estándar de longitud del péndulo siguió siendo popular, porque se descubrió que la gravedad solo varía con la latitud . La aceleración gravitacional aumenta suavemente desde el ecuador hasta los polos , debido a la forma achatada de la Tierra, por lo que en cualquier latitud dada (línea este-oeste), la gravedad era lo suficientemente constante como para que la longitud de un péndulo de segundos fuera la misma dentro de la capacidad de medición del siglo XVIII. Por lo tanto, la unidad de longitud podría definirse en una latitud dada y medirse en cualquier punto a lo largo de esa latitud. Por ejemplo, un péndulo estándar definido en la latitud 45° norte, una opción popular, podría medirse en partes de Francia, Italia, Croacia, Serbia, Rumania, Rusia, Kazajstán, China, Mongolia, Estados Unidos y Canadá. Además, podría recrearse en cualquier lugar en el que se hubiera medido con precisión la aceleración gravitacional.
A mediados del siglo XIX, las mediciones de péndulo cada vez más precisas realizadas por Edward Sabine y Thomas Young revelaron que la gravedad, y por lo tanto la longitud de cualquier péndulo estándar, variaban de forma mensurable con las características geológicas locales, como las montañas y las rocas densas del subsuelo. [127] Por lo tanto, un estándar de longitud de péndulo debía definirse en un único punto de la Tierra y solo podía medirse allí. Esto le quitó gran parte del atractivo al concepto y se abandonaron los esfuerzos por adoptar estándares de péndulo.
Propuestas tempranas
Uno de los primeros en sugerir definir la longitud con un péndulo fue el científico flamenco Isaac Beeckman [128], quien en 1631 recomendó hacer del péndulo de segundos "la medida invariable para todas las personas en todo momento y en todos los lugares". [129] Marin Mersenne , quien midió por primera vez el péndulo de segundos en 1644, también lo sugirió. La primera propuesta oficial para un estándar de péndulo fue hecha por la Royal Society británica en 1660, defendida por Christiaan Huygens y Ole Rømer , basándose en el trabajo de Mersenne, [130] y Huygens en Horologium Oscillatorium propuso un "pie horario" definido como 1/3 del péndulo de segundos. Christopher Wren fue otro de los primeros partidarios. La idea de un estándar de péndulo de longitud debe haber sido familiar para la gente ya en 1663, porque Samuel Butler la satiriza en Hudibras : [131]
- En el banco los trataré así
- Que la vibración de este péndulo
- Hará que todos los patios de los sastres sean de uno solo
- Opinión unánime
En 1671, Jean Picard propuso un «pie universal» definido mediante un péndulo en su influyente Mesure de la Terre . [132] Gabriel Mouton, alrededor de 1670, sugirió definir la toesa mediante un péndulo de segundos o un minuto de grado terrestre. En 1675, el erudito italiano Tito Livio Burratini propuso un plan para un sistema completo de unidades basado en el péndulo. En Francia, en 1747, el geógrafo Charles Marie de la Condamine propuso definir la longitud mediante un péndulo de segundos en el ecuador; ya que en esta ubicación el movimiento del péndulo no se distorsionaría por la rotación de la Tierra. James Steuart (1780) y George Skene Keith también fueron partidarios.
A finales del siglo XVIII, cuando muchas naciones estaban reformando sus sistemas de pesaje y medida , el péndulo de segundos era la opción principal para una nueva definición de longitud, defendida por científicos destacados en varias naciones importantes. En 1790, el entonces Secretario de Estado de los EE. UU., Thomas Jefferson, propuso al Congreso un "sistema métrico" estadounidense decimalizado integral basado en el péndulo de segundos a 38° de latitud norte, la latitud media de los Estados Unidos. [133] No se tomó ninguna medida sobre esta propuesta. En Gran Bretaña, el principal defensor del péndulo fue el político John Riggs Miller . [134] Cuando sus esfuerzos por promover un sistema métrico conjunto británico-francés-estadounidense fracasaron en 1790, propuso un sistema británico basado en la longitud del péndulo de segundos en Londres. Esta norma se adoptó en 1824 (abajo).
El metro
En las discusiones que llevaron a la adopción del sistema métrico decimal por Francia en 1791, el candidato principal para la definición de la nueva unidad de longitud, el metro , fue el péndulo de segundos a 45° de latitud norte. Fue defendido por un grupo liderado por el político francés Talleyrand y el matemático Antoine Nicolas Caritat de Condorcet . Esta fue una de las tres opciones finales consideradas por el comité de la Academia Francesa de Ciencias . Sin embargo, el 19 de marzo de 1791, el comité optó por basar el metro en la longitud del meridiano que pasa por París. Se rechazó una definición de péndulo debido a su variabilidad en diferentes lugares y porque definía la longitud por una unidad de tiempo. (Sin embargo, desde 1983 el metro se ha definido oficialmente en términos de la longitud del segundo y la velocidad de la luz). Una posible razón adicional es que la radical Academia Francesa no quería basar su nuevo sistema en el segundo, una unidad tradicional y no decimal del antiguo régimen .
Aunque no está definida por el péndulo, la longitud final elegida para el metro, 10 −7 del arco meridiano de polo a ecuador , era muy cercana a la longitud del péndulo de segundos (0,9937 m), con una diferencia de 0,63 %. Aunque en su momento no se dio ninguna razón para esta elección en particular, probablemente fue para facilitar el uso del péndulo de segundos como un estándar secundario, como se propuso en el documento oficial. Por lo tanto, la unidad de longitud estándar del mundo moderno está ciertamente estrechamente vinculada históricamente con el péndulo de segundos.
Gran Bretaña y Dinamarca
Gran Bretaña y Dinamarca parecen ser las únicas naciones que (por un corto tiempo) basaron sus unidades de longitud en el péndulo. En 1821, la pulgada danesa se definió como 1/38 de la longitud del péndulo de segundos solares medio a 45° de latitud en el meridiano de Skagen , al nivel del mar, en el vacío. [135] [136] El parlamento británico aprobó la Ley Imperial de Pesos y Medidas en 1824, una reforma del sistema estándar británico que declaraba que si se destruía el prototipo de yarda estándar , se recuperaría definiendo la pulgada de modo que la longitud del péndulo de segundos solares en Londres, al nivel del mar , en el vacío, a 62 °F fuera 39,1393 pulgadas. [137] Esto también se convirtió en el estándar estadounidense, ya que en ese momento Estados Unidos usaba medidas británicas. Sin embargo, cuando el prototipo de patio se perdió en el incendio de las Cámaras del Parlamento en 1834 , resultó imposible recrearlo con precisión a partir de la definición de péndulo, y en 1855 Gran Bretaña derogó el estándar del péndulo y volvió a los estándares de prototipos.
Otros usos
Sismómetros
En los primeros sismómetros se utilizaba un péndulo en el que la varilla no estaba vertical sino casi horizontal para medir los temblores de tierra. La masa del péndulo no se mueve cuando lo hace su soporte y la diferencia de movimientos se registra en un diagrama de tambor.
Afinación Schuler
Como lo explicó por primera vez Maximilian Schuler en un artículo de 1923, un péndulo cuyo período es exactamente igual al período orbital de un satélite hipotético que orbita justo por encima de la superficie de la Tierra (unos 84 minutos) tenderá a permanecer apuntando al centro de la Tierra cuando su soporte se desplace repentinamente. Este principio, llamado ajuste de Schuler , se utiliza en sistemas de guía inercial en barcos y aviones que operan en la superficie de la Tierra. No se utiliza ningún péndulo físico, pero el sistema de control que mantiene estable la plataforma inercial que contiene los giroscopios se modifica para que el dispositivo actúe como si estuviera unido a dicho péndulo, manteniendo la plataforma siempre hacia abajo mientras el vehículo se mueve sobre la superficie curva de la Tierra.
Péndulos acoplados

.jpg/440px-Huygens_synchronization_of_two_clocks_(Experiment).jpg)
En 1665, Huygens hizo una curiosa observación sobre los relojes de péndulo. Había colocado dos relojes sobre la repisa de su chimenea y notó que habían adquirido un movimiento opuesto. Es decir, sus péndulos latían al unísono pero en dirección opuesta; 180° desfasados . Independientemente de cómo se pusieran en marcha los dos relojes, descubrió que eventualmente volverían a este estado, haciendo así la primera observación registrada de un oscilador acoplado . [138]
La causa de este comportamiento era que los dos péndulos se afectaban entre sí a través de ligeros movimientos de la repisa de apoyo. Este proceso se denomina arrastre o bloqueo de modo en física y se observa en otros osciladores acoplados. Los péndulos sincronizados se han utilizado en relojes y se utilizaron ampliamente en gravímetros a principios del siglo XX. Aunque Huygens solo observó sincronización desfasada, investigaciones recientes han demostrado la existencia de sincronización en fase, así como estados de "muerte" en los que uno o ambos relojes se detienen. [139] [140]
Práctica religiosa

El movimiento del péndulo también aparece en las ceremonias religiosas. El incensario oscilante , también conocido como turíbulo , es un ejemplo de péndulo. [141] Los péndulos también se ven en muchas reuniones en el este de México, donde marcan el cambio de mareas el día en que estas se encuentran en su punto más alto. Véase también péndulos para adivinación y radiestesia .
Educación
Los péndulos se utilizan ampliamente en la educación científica como un ejemplo de un oscilador armónico , para enseñar dinámica y movimiento oscilatorio . Un uso es demostrar la ley de conservación de la energía . [142] [143] Un objeto pesado como una bola de bolos [144] o una bola de demolición [142] se ata a una cuerda. Luego, el peso se mueve a unos pocos centímetros de la cara de un voluntario, luego se suelta y se le permite oscilar y regresar. En la mayoría de los casos, el peso invierte la dirección y luego regresa a (casi) la misma posición que la ubicación de liberación original, es decir , a una pequeña distancia de la cara del voluntario, lo que deja al voluntario ileso. En ocasiones, el voluntario se lesiona si no se queda quieto [145] o el péndulo se suelta inicialmente con un empujón (de modo que cuando regresa sobrepasa la posición de liberación).
Dispositivo de tortura

Se afirma que el péndulo fue utilizado como instrumento de tortura y ejecución por la Inquisición española [146] en el siglo XVIII. La acusación está contenida en el libro de 1826 La historia de la Inquisición de España del sacerdote, historiador y activista liberal español Juan Antonio Llorente . [147] Un péndulo oscilante cuyo borde es la hoja de un cuchillo desciende lentamente hacia un prisionero atado hasta que corta su cuerpo. [148] Este método de tortura llegó a la conciencia popular a través del cuento de 1842 " El pozo y el péndulo " del autor estadounidense Edgar Allan Poe [149] pero existe un escepticismo considerable sobre su uso real.
La mayoría de las fuentes bien informadas son escépticas sobre si esta tortura se utilizó realmente. [150] [151] [152] La única evidencia de su uso es un párrafo en el prefacio de la Historia de Llorente de 1826 , [147] que relata un relato de segunda mano de un solo prisionero liberado de la mazmorra de la Inquisición en Madrid en 1820, que supuestamente describió el método de tortura del péndulo. Las fuentes modernas señalan que debido a la advertencia de Jesús contra el derramamiento de sangre, a los inquisidores solo se les permitía usar métodos de tortura que no derramaran sangre, y el método del péndulo habría violado esta restricción. Una teoría es que Llorente entendió mal el relato que escuchó; el prisionero en realidad se refería a otra tortura común de la Inquisición, el strappado (garrucha), en la que el prisionero tiene las manos atadas a la espalda y es levantado del suelo con una cuerda atada a sus manos. [152] Este método también se conocía como el "péndulo". El popular cuento de terror de Poe y el conocimiento público de otros métodos brutales de la Inquisición han mantenido vivo el mito de este elaborado método de tortura.
Onda de péndulo
Una onda de péndulo es una demostración de física y arte cinético que comprende varios péndulos desacoplados con diferentes longitudes. A medida que los péndulos oscilan, parecen producir ondas viajeras y estacionarias, vibraciones y movimiento aleatorio. [153]
Véase también
- Los péndulos de Barton
- Péndulo de Blackburn
- Péndulo cónico
- Péndulo cicloidal
- Péndulo doble
- Péndulo doble invertido
- El péndulo de Doubochinski
- Péndulo de Foucault
- Péndulo de Furuta
- Péndulo de parrilla
- Armonógrafo (también conocido como "péndulo de Lissajous")
- Péndulo de rueda de inercia
- Péndulo invertido
- El péndulo de Kapitza
- El péndulo de Kater
- Metrónomo
- Péndulo N [154]
- Péndulo (mecánica)
- Reloj de péndulo
- Falacia del cohete de péndulo
- Péndulo cuántico
- Péndulo de Rayleigh-Lorentz
- Péndulo de segundos
- Movimiento armónico simple
- Péndulo esférico
- Péndulo de resorte
- Péndulo de torsión
Notas
- ^ Una oscilación "pequeña" es aquella en la que el ángulo θ es lo suficientemente pequeño como para que sen( θ ) pueda aproximarse por θ cuando θ se mide en radianes.
- ^ El valor de "g" (aceleración debida a la gravedad) en el ecuador es 9,780 m/s 2 y en los polos es 9,832 m/s 2 , una diferencia de 0,53%.
El valor de g reflejado por el período de un péndulo varía de un lugar a otro. La fuerza gravitatoria varía con la distancia al centro de la Tierra, es decir, con la altitud, o debido a que la Tierra tiene forma achatada, g varía con la latitud. Una causa más importante de esta reducción de g en el ecuador es que el ecuador gira a una revolución por día, por lo que la aceleración de la fuerza gravitatoria se cancela parcialmente allí por la fuerza centrífuga .
Referencias
- ^ "Péndulo". Enciclopedia universitaria de Miriam Webster . Miriam Webster. 2000. pág. 1241. ISBN 978-0-87779-017-4.
- ^ abcdefg Marrison, Warren (1948). "La evolución del reloj de cristal de cuarzo". Bell System Technical Journal . 27 (3): 510–588. doi :10.1002/j.1538-7305.1948.tb01343.x. Archivado desde el original el 17 de julio de 2011.
- ^ Morris, William, Ed. (1979). The American Heritage Dictionary, New College Ed. Nueva York: Houghton-Mifflin. pág. 969. ISBN 978-0-395-20360-6.
{{cite book}}: CS1 maint: varios nombres: lista de autores ( enlace ) - ^ Levien, RB; Tan, SM (1993). "Péndulo doble: un experimento en el caos". American Journal of Physics . 61 (11): 1038. Bibcode :1993AmJPh..61.1038L. doi :10.1119/1.17335.
- ^ definido por Christiaan Huygens: Huygens, Christian (1673). "Horologium Oscillatorium" (PDF) . Matemáticas del siglo XVII . 17thcenturymaths.com . Consultado el 1 de marzo de 2009 ., Parte 4, Definición 3, traducido en julio de 2007 por Ian Bruce
- ^ ab Nave, Carl R. (2006). "Péndulo simple". Hiperfísica . Universidad Estatal de Georgia . Consultado el 10 de diciembre de 2008 .
- ^ Xue, Linwei (2007). "Sistemas de péndulo". Ver y tocar conceptos estructurales . Departamento de Ingeniería Civil, Universidad de Manchester, Reino Unido . Consultado el 10 de diciembre de 2008 .
- ^ Weisstein, Eric W. (2007). "Péndulo simple". El mundo científico de Eric Weisstein . Wolfram Research . Consultado el 9 de marzo de 2009 .
- ^ abcdefghi Milham, Willis I. (1945). Tiempo y cronometradores . MacMillan., pág. 188-194
- ^ Halliday, David; Robert Resnick; Jearl Walker (1997). Fundamentos de física, 5.ª edición . Nueva York: John Wiley & Sons. pág. 381. ISBN. 978-0-471-14854-8.
- ^ Cooper, Herbert J. (2007). Scientific Instruments. Nueva York: Hutchinson's. pág. 162. ISBN 978-1-4067-6879-4.
- ^ ab Nelson, Robert; MG Olsson (febrero de 1987). "El péndulo: física enriquecida a partir de un sistema simple" (PDF) . American Journal of Physics . 54 (2): 112–121. Bibcode :1986AmJPh..54..112N. doi :10.1119/1.14703. S2CID 121907349 . Consultado el 29 de octubre de 2008 .
- ^ Penderel-Brodhurst, James George Joseph (1911). . En Chisholm, Hugh (ed.). Encyclopædia Britannica . Vol. 06 (11.ª ed.). Cambridge University Press. pp. 536–553, véase página 538.
Péndulo. Supongamos que tenemos un cuerpo...
incluye una derivación - ^ Deschaine, JS; Suits, BH (2008). "La cuerda colgante con una masa real en la punta". Revista Europea de Física . 29 (6): 1211–1222. Bibcode :2008EJPh...29.1211D. doi :10.1088/0143-0807/29/6/010. S2CID 122637957.
- ^ ab Huygens, Christian (1673). "Horologium Oscillatorium". 17centurymaths . Traducido por Bruce, Ian. 17thcenturymaths.com . Consultado el 1 de marzo de 2009 ., Parte 4, Proposición 5
- ^ Glasgow, David (1885). Fabricación de relojes. Londres: Cassel & Co., pág. 278.
- ^ Fowles, Grant R (1986). Mecánica analítica, 4ª ed . Nueva York, Nueva York: Saunders. págs. 202 y siguientes.
- ^ abc Huygens (1673) Horologium Oscillatorium, parte 4, proposición 20
- ^ Morton, W. Scott y Charlton M. Lewis (2005). China: su historia y cultura. Nueva York: McGraw-Hill, Inc., pág. 70
- ^ de Needham, Volumen 3, 627-629
- ^ Good, Gregory (1998). Ciencias de la Tierra: una enciclopedia de eventos, personas y fenómenos. Routledge. pág. 394. ISBN 978-0-8153-0062-5.
- ^ "ibn+yunus"+pendulum&pg=RA2-PA126 "Péndulo". Enciclopedia Americana . Vol. 21. The Americana Corp. 1967. p. 502. ISBN 978-0-19-538207-5. Consultado el 20 de febrero de 2009 .
- ^ Baker, Cyril Clarence Thomas (1961). Diccionario de matemáticas. G. Newnes. pág. 176.
- ^ Newton, Roger G. (2004). El péndulo de Galileo: del ritmo del tiempo a la creación de la materia . EE. UU.: Harvard University Press. pág. 52. ISBN 978-0-674-01331-5.
- ^ King, DA (1979). «Ibn Yunus y el péndulo: una historia de errores». Archives Internationales d'Histoire des Sciences . 29 (104): 35–52., reimpreso en el sitio web Muslim Heritage.
- ^ Hall, Bert S. (septiembre de 1978). "El péndulo escolástico". Anales de la ciencia . 35 (5): 441–462. doi :10.1080/00033797800200371. ISSN 0003-3790.
- ^ O'Connor, JJ; Robertson, EF (noviembre de 1999). "Abu'l-Hasan Ali ibn Abd al-Rahman ibn Yunus". Universidad de St Andrews . Consultado el 29 de mayo de 2007 .
- ^ Akyeampong, Emmanuel K.; Gates, Henry Louis Jr., eds. (2012). "Ibn Yunus" . Diccionario de biografías africanas . Vol. 3. Oxford Univ. Press. págs. 126–127. ISBN 978-0-19-538207-5.
- ^ Matthews, Michael R. (2000). La hora de la educación científica. Springer. pág. 87. ISBN 978-0-306-45880-4.
- ^ Drake, Stillman (2003). Galileo en acción: su biografía científica. Estados Unidos: Courier Dover. pp. 20-21. ISBN 978-0-486-49542-2.
- ^ Galileo, Galileo; Drabkin, IE; Drake, Stillman (1960). Sobre el movimiento y sobre la mecánica . Madison: Universidad de Wisconsin. pág. 108.
- ^ Drake, Stillman (2003). Galileo en acción: su biografía científica. Estados Unidos: Courier Dover. pág. 17. ISBN 978-0-486-49542-2.
- ^ Galilei, Galileo (1909). Favaro, Antonio [en italiano] (ed.). Le Opere di Galileo Galilei, Edizione Nazionale [ Las obras de Galileo Galilei, edición nacional ] (en italiano). Florencia : Barberá. ISBN 978-88-09-20881-0.
- ^ Murdin, Paul (2008). Meridiano completo de gloria: peligrosas aventuras en la competencia para medir la Tierra. Springer. pág. 41. ISBN 978-0-387-75533-5.
- ^ La Lampada di Galileo, de Francesco Malaguzzi Valeri, para Archivio storico dell'arte, Volumen 6 (1893); Editor, Domenico Gnoli; Editorial Danesi, Roma; Página 215-218.
- ^ ab Van Helden, Albert (1995). "Reloj de péndulo". El Proyecto Galileo . Universidad del Arroz . Consultado el 25 de febrero de 2009 .
- ^ Bigotti, Fabrizio; Taylor, David (2017). "El pulsilogium de Santorio: nueva luz sobre la tecnología y la medición en la medicina moderna temprana". Societate Si Politica . 11 (2): 53–113. ISSN 1843-1348. PMC 6407692 . PMID 30854144.
- ^ Drake 2003, págs. 419-420
- ^ aunque existen referencias no confirmadas a relojes de péndulo anteriores fabricados por otros: Usher, Abbott Payson (1988). A History of Mechanical Inventions. Courier Dover. pp. 310–311. ISBN 978-0-486-25593-4.
- ^ Eidson, John C. (2006). Medición, control y comunicación utilizando IEEE 1588. Burkhausen. pág. 11. ISBN 978-1-84628-250-8.
- ^ Milham 1945, pág. 145
- ^ ab O'Connor, JJ; EF Robertson (agosto de 2002). "Robert Hooke". Biografías, Archivo de Historia de las Matemáticas de MacTutor . Facultad de Matemáticas y Estadística, Universidad de St. Andrews, Escocia. Archivado desde el original el 3 de marzo de 2009. Consultado el 21 de febrero de 2009 .
- ^ Nauenberg, Michael (2006). "La contribución fundamental de Robert Hooke a la dinámica orbital". Robert Hooke: Estudios del tricentenario . Ashgate Publishing. págs. 17-19. ISBN 0-7546-5365-X.
- ^ Nauenberg, Michael (2004). "Hooke y Newton: adivinando los movimientos planetarios". Physics Today . 57 (2): 13. Bibcode :2004PhT....57b..13N. doi : 10.1063/1.1688052 . Consultado el 30 de mayo de 2007 .
- ^ The KGM Group, Inc. (2004). "Modelos heliocéntricos". Science Master. Archivado desde el original el 13 de julio de 2007. Consultado el 30 de mayo de 2007 .
- ^ Lenzen, Victor F.; Robert P. Multauf (1964). "Documento 44: Desarrollo de péndulos de gravedad en el siglo XIX". Boletín 240 del Museo Nacional de los Estados Unidos: Contribuciones del Museo de Historia y Tecnología reimpreso en Boletín del Instituto Smithsoniano . Washington: Smithsonian Institution Press. p. 307. Consultado el 28 de enero de 2009 .
- ^ Más rico, Jean (1679). Observaciones astronómicas y físicas hechas en la isla de Caïenne . Memorias de la Academia Real de Ciencias. Código bibliográfico : 1679oaep.book.....R.citado en Lenzen & Multauf, 1964, p.307
- ^ Lenzen y Multauf, 1964, p.307
- ^ Poynting, John Henry; Joseph John Thompson (1907). Un libro de texto de física, 4.ª edición. Londres: Charles Griffin & Co., págs. 20-22.
- ^ Huygens, Christian; traducido por Ian Bruce (julio de 2007). "Horologium Oscillatorium" (PDF) . 17centurymaths . 17thcenturymaths.com . Consultado el 1 de marzo de 2009 .
- ^ La constelación de Horologium recibió posteriormente el nombre en honor a este libro.
- ^ Matthews, Michael R. (1994). Enseñanza de las ciencias: el papel de la historia y la filosofía de la ciencia. Psychology Press. pp. 121–122. ISBN 978-0-415-90899-3.
- ^ Huygens, Horologium Oscillatorium, parte 2, proposición 25
- ^ Mahoney, Michael S. (19 de marzo de 2007). «Christian Huygens: La medición del tiempo y de la longitud en el mar». Universidad de Princeton. Archivado desde el original el 4 de diciembre de 2007. Consultado el 27 de mayo de 2007 .
- ^ Bevilaqua, Fabio; Lidia Falomo; Lucio Fregonese; Enrico Gianetto; Franco Giudise; Paolo Mascheretti (2005). "El péndulo: de la caída forzada al concepto de potencial". El péndulo: perspectivas científicas, históricas, filosóficas y educativas . Springer. págs. 195–200. ISBN 1-4020-3525-X. Consultado el 26 de febrero de 2008 .Da una descripción detallada de los métodos de Huygens.
- ^ ab Headrick, Michael (2002). "Origen y evolución del escape del reloj de ancla". Revista de sistemas de control, Inst. de ingenieros eléctricos y electrónicos . 22 (2). Archivado desde el original el 25 de octubre de 2009. Consultado el 6 de junio de 2007 .
- ^ " ... se ve afectado por la intemperancia del aire o por cualquier defecto en el mecanismo, de modo que el QR de la muleta no siempre se activa con la misma fuerza... Con arcos grandes, las oscilaciones tardan más, en la forma que he explicado, por lo que existen algunas desigualdades en el movimiento del reloj por esta causa... ", Huygens, Christiaan (1658). Horologium (PDF) . La Haya: Adrian Vlaqc., traducción de Ernest L. Edwardes (diciembre de 1970) Antiquarian Horology , vol. 7, n.º 1
- ^ ab Andrewes, WJH Relojes y relojes: el salto a la precisión en Macey, Samuel (1994). Enciclopedia del tiempo . Taylor & Francis. págs. 123–125. ISBN 978-0-8153-0615-3.
- ^ Usher, 1988, pág. 312
- ^ de Beckett, Edmund (1874). Tratado rudimentario sobre relojes y campanas, 6.ª ed. Londres: Lockwood & Co., pág. 50.
- ^ ab Graham, George (1726). "Un mecanismo para evitar irregularidades en el movimiento de un reloj ocasionadas por la acción del calor y el frío sobre la varilla del péndulo". Philosophical Transactions of the Royal Society . 34 (392–398): 40–44. doi : 10.1098/rstl.1726.0006 . S2CID 186210095.citado en Day, Lance; Ian McNeil (1996). Diccionario biográfico de la historia de la tecnología. Taylor & Francis. pág. 300. ISBN 978-0-415-06042-4.
- ^ ab Kater, Henry (1818). "Relato de experimentos para determinar la longitud de los segundos de vibración del péndulo en la latitud de Londres". Phil. Trans. R. Soc . 104 (33): 109. Consultado el 25 de noviembre de 2008 .
- ^ Oprea, John (1995). "Geometría y el péndulo de Focault" (PDF) . The American Mathematical Monthly . 102 (6). Asociación Matemática de Estados Unidos: 515–522. doi :10.1080/00029890.1995.12004611. Archivado (PDF) desde el original el 9 de octubre de 2022. Consultado el 13 de abril de 2021 .
- ^ Amir Aczel (2003) Leon Foucault: Su vida, época y logros, en Matthews, Michael R.; Colin F. Gauld; Arthur Stinner (2005). El péndulo: perspectivas científicas, históricas, educativas y filosóficas. Springer. pág. 177. ISBN 978-1-4020-3525-8.
- ^ Giovannangeli, Françoise (noviembre de 1996). "El péndulo de Foucault girando en el Panteón". Páginas de París. Archivado desde el original el 9 de junio de 2007. Consultado el 25 de mayo de 2007 .
- ^ Tobin, William (2003). La vida y la ciencia de León Foucault: el hombre que demostró que la Tierra gira. Reino Unido: Cambridge University Press. pp. 148-149. ISBN 978-0-521-80855-2.
- ^ abcd Penderel-Brodhurst, James George Joseph (1911). . En Chisholm, Hugh (ed.). Encyclopædia Britannica . Vol. 06 (11.ª ed.). Cambridge University Press. págs. 536–553, véanse las páginas 540 y 541.
- ^ abc Jones, Tony (2000). Dividiendo el segundo: la historia del tiempo atómico. CRC Press. p. 30. ISBN 978-0-7503-0640-9.
- ^ Kaler, James B. (2002). El cielo en constante cambio: una guía sobre la esfera celestial. Reino Unido: Cambridge Univ. Press. p. 183. ISBN 978-0-521-49918-7.
- ^ Audoin, Claude; Bernard Guinot; Stephen Lyle (2001). La medición del tiempo: tiempo, frecuencia y el reloj atómico. Reino Unido: Cambridge Univ. Press. p. 83. ISBN 978-0-521-00397-1.
- ^ ab Torge, Wolfgang (2001). Geodesia: una introducción. Walter de Gruyter. pag. 177.ISBN 978-3-11-017072-6.
- ^ Milham 1945, pág. 334
- ^ calculado a partir de la ecuación (1)
- ^ Glasgow, David (1885). Fabricación de relojes. Londres: Cassel & Co., págs. 279-284.
- ^ Matthys, Robert J. (2004). Relojes de péndulo precisos. Reino Unido: Oxford Univ. Press. p. 4. ISBN 978-0-19-852971-2.
- ^ Mattheys, 2004, pág. 13
- ^ Matthys 2004, págs. 91-92
- ^ Beckett 1874, pág. 48
- ^ "Reglamento". Enciclopedia de relojes y relojes . Mercado de antigüedades antiguas y vendidas. 2006. Consultado el 9 de marzo de 2009 .
- ^ Beckett 1874, pág. 43
- ^ Glasgow 1885, pág. 282
- ^ "Datos sobre el Gran Reloj". Big Ben . Londres: Parlamento del Reino Unido. 13 de noviembre de 2009. Archivado desde el original el 7 de octubre de 2009 . Consultado el 31 de octubre de 2012 .
- ^ Matthys 2004, pág. 3
- ^ abcd Penderel-Brodhurst, James George Joseph (1911). . En Chisholm, Hugh (ed.). Encyclopædia Britannica . Vol. 06 (11.ª ed.). Cambridge University Press. págs. 536–553, véanse las páginas 539 y 540.
- ^ Huygens, Christiaan (1658). Relojería (PDF) . La Haya: Adrian Vlaqc., traducción de Ernest L. Edwardes (diciembre de 1970) Antiquarian Horology , vol. 7, n.º 1
- ^ Zupko, Ronald Edward (1990). Revolución en la medición: pesos y medidas en Europa occidental desde la era de la ciencia . Diane Publishing. pág. 131. ISBN 978-0-87169-186-6.
- ^ Picard, Jean (1671). La Mesure de la Terre [ La medida de la Tierra ] (en francés). París, Francia: Imprimerie Royale. pag. 4.Picard describió un péndulo que consistía en una bola de cobre de una pulgada (2,54 mm) de diámetro y que estaba suspendida de una hebra de pite , una fibra de la planta de aloe. Picard luego menciona que la temperatura afecta levemente la longitud de este péndulo: "Es cierto que esta longitud [del péndulo] no siempre se encuentra [tan precisa], y que parecía que siempre debería acortarse un poco en invierno y alargarse en verano; pero es solo una décima parte de una línea..." [1 línea (línea) = 2,2558 mm].
- ^ abcd Matthys 2004, págs. 7-12
- ^ Milham 1945, pág. 335
- ^ Milham 1945, pág. 331-332
- ^ Matthys 2004, Parte 3, págs. 153-179
- ^ Poynting y Thompson, 1907, págs. 13-14
- ^ Updegraff, Milton (7 de febrero de 1902). "Sobre la medición del tiempo". Science . 15 (371): 218–219. doi :10.1126/science.ns-15.374.218-a. PMID 17793345. S2CID 21030470 . Consultado el 13 de julio de 2009 .
- ^ Dunwoody, Halsey (1917). Notas, problemas y ejercicios de laboratorio sobre mecánica, sonido, luz, termomecánica e hidráulica, 1.ª ed. Nueva York: John Wiley & Sons. pág. 87.
- ^ "Ancho de resonancia". Glosario . División de tiempo y frecuencia, Instituto Nacional de Estándares y Tecnología de EE. UU. 2009. Archivado desde el original el 30 de enero de 2009 . Consultado el 21 de febrero de 2009 .
- ^ ab Jespersen, James; Fitz-Randolph, Jane; Robb, John (1999). De los relojes de sol a los relojes atómicos: comprensión del tiempo y la frecuencia. Nueva York: Courier Dover. págs. 41–50. ISBN 978-0-486-40913-9.pág.39
- ^ Matthys, Robert J. (2004). Relojes de péndulo precisos. Reino Unido: Oxford Univ. Press. pp. 27–36. ISBN 978-0-19-852971-2.Tiene una excelente discusión completa de la controversia sobre la aplicabilidad de Q a la precisión de los péndulos.
- ^ "Factor de calidad, Q". Glosario . División de tiempo y frecuencia, Instituto Nacional de Normas y Tecnología de EE. UU. 2009. Archivado desde el original el 4 de mayo de 2008 . Consultado el 21 de febrero de 2009 .
- ^ Matthys, 2004, p.32, fig. 7.2 y texto
- ^ Matthys, 2004, pág. 81
- ^ abc "Q, Factor de calidad". Revista de relojes . Sitio web de Orologeria Lamberlin . Consultado el 21 de febrero de 2009 .
- ^ Milham 1945, pág. 615
- ^ "Los relojes Reifler y Shortt". Instituto JagAir de Tiempo y Tecnología . Consultado el 29 de diciembre de 2009 .
- ^ Betts, Jonathan (22 de mayo de 2008). "Declaración del experto, caso 6 (2008-09) William Hamilton Shortt, regulador". Audiencia sobre licencias de exportación, Comité de Revisión de la Exportación de Obras de Arte y Objetos de Interés Cultural . Consejo de Museos, Bibliotecas y Archivos del Reino Unido. Archivado desde el original (DOC) el 25 de octubre de 2009. Consultado el 29 de diciembre de 2009 .
- ^ Airy, George Biddle (26 de noviembre de 1826). "Sobre las perturbaciones de péndulos y balanzas y sobre la teoría de los escapes". Transactions of the Cambridge Philosophical Society . 3 (Parte 1): 105 . Consultado el 25 de abril de 2008 .
- ^ Beckett 1874, págs. 75-79
- ^ Vočadlo, Lidunka. "Gravedad, forma de la Tierra, isostasia, momento de inercia" . Consultado el 5 de noviembre de 2012 .
- ^ Baker, Lyman A. (primavera de 2000). "Chancellor Bacon". Inglés 233 – Introducción a las humanidades occidentales . Departamento de inglés, Universidad Estatal de Kansas . Consultado el 20 de febrero de 2009 .
- ^ de Poynting y Thompson 1907, pág. 9
- ^ Poynting, John Henry; Joseph John Thompson (1907). Un libro de texto de física, 4.ª edición. Londres: Charles Griffin & Co., pág. 20.
- ^ ab Victor F., Lenzen; Robert P. Multauf (1964). "Documento 44: Desarrollo de péndulos de gravedad en el siglo XIX". Boletín 240 del Museo Nacional de los Estados Unidos: Contribuciones del Museo de Historia y Tecnología reimpreso en Boletín del Instituto Smithsoniano . Washington: Smithsonian Institution Press. p. 307. Consultado el 28 de enero de 2009 .
- ^ de Poynting y Thompson, 1907, pág. 10
- ^ Poynting, John Henry (1894). La densidad media de la Tierra. Londres: Charles Griffin. pp. 22–24.
- ^ Harper, William L. (diciembre de 2011). "Christiaan Huygens: un gran filósofo natural que midió la gravedad y una luz de esperanza para Newton sobre el método". El método científico de Isaac Newton: convertir los datos en evidencia sobre la gravedad y la cosmología . doi :10.1093/acprof:oso/9780199570409.003.0005.
- ^ Cox, John (1904). Mecánica. Cambridge, Reino Unido: Cambridge Univ. Press. pp. 311–312.
- ^ Poynting y Thomson 1904, pág. 23
- ^ Poynting, John Henry (1894). La densidad media de la Tierra. Londres: Charles Griffin & Co., págs. 24-29.
- ^ Poynting, John Henry (1911). . En Chisholm, Hugh (ed.). Encyclopædia Britannica . Vol. 12 (11.ª ed.). Cambridge University Press. pp. 384–389, véase la página 386.
Experimento de Airy. En 1854 Sir GB Airy...
- ^ Lenzen y Multauf 1964, p.320
- ^ Poynting y Thompson 1907, pág. 18
- ^ abc "Los altibajos de los estudios de gravedad". NOAA celebra 200 años . Administración Nacional Oceánica y Atmosférica de Estados Unidos. 9 de julio de 2007.
- ^ Lenzen y Multauf 1964, p.324
- ^ Lenzen y Multauf 1964, p.329
- ^ ab Woolard, George P. (28-29 de junio de 1957). "Observaciones de gravedad durante el Año Geofísico Internacional". Geofísica y el Año Geofísico Internacional: Actas del simposio de apertura del Año Geofísico Internacional . Washington, DC: American Geophysical Union, Nat'l Academy of Sciences. p. 200. Consultado el 27 de mayo de 2009 .
- ^ Lenzen y Multauf 1964, p.336, figura 28
- ^ de Michael R., Matthews (2001). "Metodología y política en la ciencia: el destino de la propuesta de Huygens de 1673 del péndulo como estándar internacional de longitud y algunas sugerencias educativas". Ciencia, educación y cultura: la contribución de la historia y la filosofía de la ciencia . Springer. pág. 296. ISBN 0-7923-6972-6.
- ^ Renwick, James (1832). Los elementos de la mecánica. Filadelfia: Carey & Lea. págs. 286–287.
- ^ Alder, Ken (2003). La medida de todas las cosas: La odisea de siete años y el error oculto que transformó el mundo. Estados Unidos: Simon and Schuster. pág. 88. ISBN 978-0-7432-1676-0.
- ^ citado en Jourdan, Louis (22 de octubre de 2001). "Re: SI y diccionarios". USMA (lista de correo) . Consultado el 27 de enero de 2009 .
- ^ Agnoli, Paolo; Giulio D'Agostini (diciembre de 2004). "¿Por qué el metro supera al segundo?". arXiv : physics/0412078 .
- ^ citado en LeConte, John (agosto de 1885). "El sistema métrico". The Overland Monthly . 6 (2): 178 . Consultado el 4 de marzo de 2009 .
- ^ Zupko, 1990, pág. 131
- ^ Zupko, 1990, págs. 140-141
- ^ Zupko, 1990, pág. 93
- ^ Schumacher, Heinrich (1821). «Estándar danés de longitud». The Quarterly Journal of Science, Literature and the Arts . 11 (21): 184–185 . Consultado el 17 de febrero de 2009 .
- ^ "Schumacher, Heinrich Christian". The American Cyclopedia . Vol. 14. D. Appleton & Co., Londres. 1883. pág. 686 . Consultado el 17 de febrero de 2009 .
- ^ Trautwine, John Cresson (1907). The Civil Engineer's Pocket-Book, 18.ª edición. Nueva York: John Wiley. pág. 216.
- ^ Toon, John (8 de septiembre de 2000). "Fuera del tiempo: los investigadores recrean el experimento del reloj de 1665 para obtener información sobre los osciladores sincronizados modernos". Georgia Tech . Consultado el 31 de mayo de 2007 .
- ^ AL Fradkov y B. Andrievsky, "Sincronización y relaciones de fase en el movimiento de un sistema de dos péndulos", International Journal of Non-linear Mechanics, vol. 42 (2007), págs. 895–901.
- ^ II Blekhman, "Sincronización en ciencia y tecnología", ASME Press, Nueva York, 1988, (traducido del ruso al inglés)
- ^ Una simulación interesante del movimiento del incensario se puede encontrar en este sitio Archivado el 23 de mayo de 2011 en Wayback Machine .
- ^ ab Hart, Matthew (2 de febrero de 2016). «La física corre el riesgo de morir por una bola de demolición para la ciencia». Nerdist . Archivado desde el original el 15 de marzo de 2017 . Consultado el 14 de marzo de 2017 .
- ^ Sorenson, Roy (2014). "Experimentos mentales para novatos". En Booth, Anthony Robert; Rowbottom, Darrell P. (eds.). Intuiciones . Oxford Univ Pr. p. 139. ISBN 9780199609192. Recuperado el 15 de marzo de 2017 .
- ^ "Péndulo de bola de boliche". Las maravillas de la física . Universidad de Wisconsin-Madison . Consultado el 14 de marzo de 2017 .
- ^ weknowmemes (8 de agosto de 2014). "Prueba de física con pelota que salió mal". YouTube . Archivado desde el original el 10 de noviembre de 2021 . Consultado el 14 de marzo de 2017 .
- ^ Scott, George Ryley (2009). La historia de la tortura a lo largo de los siglos. Routledge. pág. 242. ISBN 978-1136191602.
- ^ ab Llorente, Juan Antonio (1826). Historia de la Inquisición en España. Abreviado y traducido por George B. Whittaker. Universidad de Oxford. pp. XX, prefacio.
- ^ Abbott, Geoffrey (2006). Ejecución: la guillotina, el péndulo, los mil cortes, el burro español y otras 66 formas de ejecutar a alguien . St. Martin's Press. ISBN 978-0-312-35222-6.
- ^ Poe, Edgar Allan (1842). El pozo y el péndulo. Booklassic. ISBN 978-9635271900.
- ^ Roth, Cecil (1964). La Inquisición española . WW Norton and Company. pp. 258. ISBN. 978-0-393-00255-3.
péndulo.
- ^ Mannix, Daniel P. (2014). La historia de la tortura. Prensa eNet. pag. 76.ISBN 978-1-61886-751-3.
- ^ ab Pavlac, Brian (2009). Caza de brujas en el mundo occidental: persecución y castigo desde la Inquisición hasta los juicios de Salem. ABC-CLIO. p. 152. ISBN 978-0-313-34874-7.
- ^ Demostraciones de la conferencia de ciencias naturales de Harvard, ondas de péndulo
- ^ Yurchenko, D.; Alevras, P. (2013). "Dinámica del péndulo N y su aplicación a un concepto de convertidor de energía de las olas". Revista Internacional de Dinámica y Control . 1 (4): 4. doi : 10.1007/s40435-013-0033-x .
Lectura adicional
- GL Baker y JA Blackburn (2009). El péndulo: un estudio de caso en física (Oxford University Press).
- M. Gitterman (2010). El péndulo caótico (World Scientific).
- Michael R. Matthews, Arthur Stinner, Colin F. Gauld (2005) El péndulo: perspectivas científicas, históricas, filosóficas y educativas , Springer
- Matthews, Michael R.; Gauld, Colin; Stinner, Arthur (2005). "El péndulo: su lugar en la ciencia, la cultura y la pedagogía". Ciencia y educación . 13 (4/5): 261–277. Bibcode :2004Sc&Ed..13..261M. doi :10.1023/b:sced.0000041867.60452.18. S2CID 195221704.
- Schlomo Silbermann, (2014) "El péndulo fundamental; el camino a ninguna parte" (libro)
- Matthys, Robert J. (2004). Relojes de péndulo precisos . Reino Unido: Oxford Univ. Press. ISBN 978-0-19-852971-2.
- Nelson, Robert; MG Olsson (febrero de 1986). "El péndulo: física rica a partir de un sistema simple". American Journal of Physics . 54 (2): 112–121. Bibcode :1986AmJPh..54..112N. doi :10.1119/1.14703. S2CID 121907349.
- LP Pook (2011). Comprensión de los péndulos: una breve introducción (Springer).



![{\displaystyle T=2\pi {\sqrt {\frac {L}{g}}}[\sum _{n=0}^{\infty }({\frac {\left(2n\right)!}{2^{2n}(n!\right)^{2}}}\right)^{2}\sin ^{2n}({\frac {\theta _{0}}{2}}\right)\right]=2\pi {\sqrt {\frac {L}{g}}}(1+{\frac {1}{16}}\theta _{0}^{2}+{\frac {11}{3072}}\theta _{0}^{4}+\cdots \right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8421cbd1dd0d5564c5f84120bb9f8a68e7e6312)


















