Mediación (estadísticas)

En estadística , un modelo de mediación busca identificar y explicar el mecanismo o proceso que subyace a una relación observada entre una variable independiente y una variable dependiente mediante la inclusión de una tercera variable hipotética, conocida como variable mediadora (también variable mediadora , variable intermediaria o variable interviniente ). ^[1] En lugar de una relación causal directa entre la variable independiente y la variable dependiente, un modelo de mediación propone que la variable independiente influye en la variable mediadora, que a su vez influye en la variable dependiente. Por lo tanto, la variable mediadora sirve para aclarar la naturaleza de la relación causal entre las variables independientes y dependientes. ^{[2] [3]}

Los análisis de mediación se emplean para comprender una relación conocida explorando el mecanismo o proceso subyacente por el cual una variable influye en otra variable a través de una variable mediadora. ^[4] En particular, el análisis de mediación puede contribuir a comprender mejor la relación entre una variable independiente y una variable dependiente cuando estas variables no tienen una conexión directa obvia.

Baron y Kenny (1986) establecieron varios requisitos que deben cumplirse para formar una verdadera relación de mediación. ^[5] A continuación, se describen utilizando un ejemplo del mundo real. Vea el diagrama anterior para obtener una representación visual de la relación de mediación general que se explicará. Los pasos originales son los siguientes.

Duración de la relación

Regrese la variable dependiente sobre la variable independiente para confirmar que la variable independiente es un predictor significativo de la variable dependiente.

Variable independiente variable dependiente${\displaystyle \to}$

${\displaystyle Y=\beta _{10}+\beta _{11}X+\varepsilon _{1}}$

• β ₁₁ es significativo

Realice una regresión del mediador sobre la variable independiente para confirmar que esta última es un predictor significativo del mediador. Si el mediador no está asociado con la variable independiente, no podría mediar nada.

Mediador variable independiente${\displaystyle \to}$

${\displaystyle Me=\beta _{20}+\beta _{21}X+\varepsilon _{2}}$

• β ₂₁ es significativo

Regrese la variable dependiente tanto en la variable mediadora como en la variable independiente para confirmar que a) el mediador es un predictor significativo de la variable dependiente, y b) la fuerza del coeficiente de la variable independiente previamente significativa en el Paso n.° 1 ahora se reduce en gran medida, si no se vuelve no significativa.

${\displaystyle Y=\beta _{30}+\beta _{31}X+\beta _{32}Me+\varepsilon _{3}}$

• β ₃₂ es significativo
• β ₃₁ debe ser menor en valor absoluto que el efecto original para la variable independiente (β ₁₁ arriba)

El siguiente ejemplo, extraído de Howell (2009), ^[6] explica cada paso de los requisitos de Baron y Kenny para comprender mejor cómo se caracteriza un efecto de mediación. El paso 1 y el paso 2 utilizan un análisis de regresión simple, mientras que el paso 3 utiliza un análisis de regresión múltiple .

1. La forma en que usted fue criado (es decir, la variable independiente) predice qué tan seguro se siente acerca de criar a sus propios hijos (es decir, la variable dependiente).
2. La forma en que usted fue criado (es decir, la variable independiente) predice sus sentimientos de competencia y autoestima (es decir, el mediador).
3. Sus sentimientos de competencia y autoestima (es decir, mediador) predicen qué tan seguro se siente acerca de criar a sus propios hijos (es decir, variable dependiente), mientras controla cómo fue criado (es decir, variable independiente).

Estos hallazgos llevarían a la conclusión de que sus sentimientos de competencia y autoestima median la relación entre la forma en que usted fue criado y la confianza que siente acerca de criar a sus propios hijos.

Si el paso 1 no produce un resultado significativo, todavía se pueden tener motivos para pasar al paso 2. A veces, en realidad existe una relación significativa entre las variables independientes y dependientes, pero debido al pequeño tamaño de las muestras u otros factores externos, podría no haber suficiente poder para predecir el efecto que realmente existe. ^[7]

En el diagrama que se muestra arriba, el efecto indirecto es el producto de los coeficientes de trayectoria "A" y "B". El efecto directo es el coeficiente "C'". El efecto directo mide el grado en que cambia la variable dependiente cuando la variable independiente aumenta en una unidad y la variable mediadora permanece inalterada. Por el contrario, el efecto indirecto mide el grado en que cambia la variable dependiente cuando la variable independiente se mantiene constante y la variable mediadora cambia en la cantidad en que habría cambiado si la variable independiente hubiera aumentado en una unidad. ^{[8] [9]}

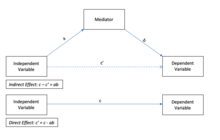
En los sistemas lineales, el efecto total es igual a la suma de los efectos directos e indirectos ( C' + AB en el modelo anterior). En los modelos no lineales, el efecto total no suele ser igual a la suma de los efectos directos e indirectos, sino a una combinación modificada de ambos. ^[9]

Una variable mediadora puede explicar toda o parte de la relación observada entre dos variables.

La evidencia máxima de mediación, también llamada mediación completa, ocurriría si la inclusión de la variable de mediación reduce la relación entre la variable independiente y la variable dependiente (ver la vía c ′ en el diagrama anterior) a cero.

La mediación parcial sostiene que la variable mediadora explica parte, pero no toda, de la relación entre la variable independiente y la variable dependiente. La mediación parcial implica que no solo existe una relación significativa entre la mediadora y la variable dependiente, sino también alguna relación directa entre la variable independiente y la variable dependiente.

Para que se establezca una mediación total o parcial, la reducción de la varianza explicada por la variable independiente debe ser significativa, tal como se determina mediante una de varias pruebas, como la prueba de Sobel . ^[10] El efecto de una variable independiente sobre la variable dependiente puede llegar a ser no significativo cuando se introduce el mediador simplemente porque se explica una cantidad trivial de varianza (es decir, no una mediación verdadera). Por lo tanto, es imperativo demostrar una reducción significativa de la varianza explicada por la variable independiente antes de afirmar una mediación total o parcial. Es posible tener efectos indirectos estadísticamente significativos en ausencia de un efecto total. ^[11] Esto puede explicarse por la presencia de varias vías de mediación que se cancelan entre sí y se vuelven perceptibles cuando se controla uno de los mediadores que se cancelan. Esto implica que los términos mediación "parcial" y "total" siempre deben interpretarse en relación con el conjunto de variables que están presentes en el modelo. En todos los casos, la operación de "fijar una variable" debe distinguirse de la de "controlar una variable", que se ha utilizado de forma inapropiada en la literatura. ^{[8] [12]} El primero significa fijar físicamente, mientras que el segundo significa condicionar, ajustar o añadir al modelo de regresión. Las dos nociones coinciden solo cuando todos los términos de error (no se muestran en el diagrama) no están correlacionados estadísticamente. Cuando los errores están correlacionados, se deben realizar ajustes para neutralizar esas correlaciones antes de embarcarse en el análisis de mediación (ver red bayesiana ).

La prueba de Sobel ^[10] se realiza para determinar si la relación entre la variable independiente y la variable dependiente se ha reducido significativamente después de la inclusión de la variable mediadora. En otras palabras, esta prueba evalúa si un efecto de mediación es significativo. Examina la relación entre la variable independiente y la variable dependiente en comparación con la relación entre la variable independiente y la variable dependiente incluyendo el factor de mediación.

La prueba de Sobel es más precisa que los pasos de Baron y Kenny explicados anteriormente; sin embargo, tiene un poder estadístico bajo. Como tal, se requieren tamaños de muestra grandes para tener suficiente poder para detectar efectos significativos. Esto se debe a que el supuesto clave de la prueba de Sobel es el supuesto de normalidad. Debido a que la prueba de Sobel evalúa una muestra dada en la distribución normal, los tamaños de muestra pequeños y la asimetría de la distribución de muestreo pueden ser problemáticos (consulte la distribución normal para obtener más detalles). Por lo tanto, la regla general sugerida por MacKinnon et al., (2002) ^[13] es que se requiere un tamaño de muestra de 1000 para detectar un efecto pequeño, un tamaño de muestra de 100 es suficiente para detectar un efecto medio y un tamaño de muestra de 50 para detectar un efecto grande.

La ecuación de Sobel es: ^[14]

${\displaystyle z={\frac {ab}{\sqrt {b^{2}s_{a}^{2}+a^{2}s_{b}^{2}}}}}$

El método bootstrap ofrece algunas ventajas con respecto a la prueba de Sobel, principalmente un aumento de potencia. El método bootstrap de Preacher y Hayes es una prueba no paramétrica y no impone el supuesto de normalidad. Por lo tanto, si se dispone de datos brutos, se recomienda el método bootstrap. ^[14] El bootstrap implica muestrear aleatoriamente de forma repetida las observaciones con reemplazo del conjunto de datos para calcular la estadística deseada en cada nueva muestra. El cálculo de cientos o miles de nuevas muestras bootstrap proporciona una aproximación de la distribución de muestreo de la estadística de interés. El método Preacher-Hayes proporciona estimaciones puntuales e intervalos de confianza mediante los cuales se puede evaluar la significancia o no significancia de un efecto de mediación. Las estimaciones puntuales revelan la media sobre el número de muestras bootstrap y si el cero no se encuentra entre los intervalos de confianza resultantes del método bootstrap, se puede concluir con seguridad que existe un efecto de mediación significativo para informar.

Como se describió anteriormente, hay algunas opciones diferentes que uno puede elegir para evaluar un modelo de mediación.

El bootstrapping ^{[15] [16]} se está convirtiendo en el método más popular para probar la mediación porque no requiere que se cumpla el supuesto de normalidad y porque se puede utilizar de manera efectiva con tamaños de muestra más pequeños ( N  < 25). Sin embargo, la mediación continúa determinándose con mayor frecuencia utilizando la lógica de Baron y Kenny ^[17] o la prueba de Sobel . Cada vez es más difícil publicar pruebas de mediación basadas puramente en el método de Baron y Kenny o pruebas que hagan supuestos distributivos como la prueba de Sobel. Por lo tanto, es importante considerar sus opciones al elegir qué prueba realizar. ^[11]

Si bien el concepto de mediación tal como se define en psicología es teóricamente atractivo, los métodos utilizados para estudiar la mediación empíricamente han sido cuestionados por estadísticos y epidemiólogos ^{[8] [12] [18]} e interpretados formalmente. ^[9]

Diseño experimental de cadena causal

Se utiliza un diseño experimental de cadena causal cuando el mediador propuesto se manipula experimentalmente. Este tipo de diseño implica que se manipula una tercera variable controlada que se tiene motivos para creer que podría ser el mecanismo subyacente de una relación determinada.

Diseño de medición de mediación

Un diseño de medición de la mediación puede conceptualizarse como un enfoque estadístico. Este diseño implica que se mide la variable interviniente propuesta y luego se utilizan análisis estadísticos para establecer la mediación. Este enfoque no implica la manipulación de la variable mediadora hipotética, sino que solo implica la medición. ^[19]

Hayes (2009) criticó el enfoque de pasos de mediación de Baron y Kenny ^[11] y, en 2019, David A. Kenny afirmó en su sitio web que la mediación puede existir en ausencia de un efecto total "significativo" (a veces denominado "mediación inconsistente") y, por lo tanto, el paso 1 del enfoque original de 1986 puede no ser necesario. Publicaciones posteriores de Hayes cuestionaron los conceptos de mediación total y mediación parcial, y abogaron por el abandono de estos términos y de los pasos de la mediación clásica (1986).

Los enfoques experimentales de la mediación deben llevarse a cabo con cautela. En primer lugar, es importante contar con un sólido respaldo teórico para la investigación exploratoria de una posible variable mediadora. Una crítica a un enfoque de mediación se basa en la capacidad de manipular y medir una variable mediadora. Por lo tanto, uno debe ser capaz de manipular el mediador propuesto de una manera aceptable y ética. Como tal, uno debe ser capaz de medir el proceso interviniente sin interferir con el resultado. El mediador también debe ser capaz de establecer la validez de constructo de la manipulación. Una de las críticas más comunes al enfoque de medición de la mediación es que, en última instancia, es un diseño correlacional. En consecuencia, es posible que alguna otra tercera variable, independiente del mediador propuesto, pueda ser responsable del efecto propuesto. Sin embargo, los investigadores han trabajado arduamente para proporcionar evidencia contraria a este menosprecio. En concreto, se han presentado los siguientes contraargumentos: ^[4]

Precedencia temporal

Por ejemplo, si la variable independiente precede a la variable dependiente en el tiempo, esto proporcionaría evidencia que sugiere un vínculo direccional, y potencialmente causal, entre la variable independiente y la variable dependiente.

No falsedad y/o ausencia de factores de confusión

Por ejemplo, si se identifican otras terceras variables y se demuestra que no alteran la relación entre la variable independiente y la variable dependiente, se tendría un argumento más sólido para afirmar su efecto de mediación. Véase otras terceras variables a continuación.

La mediación puede ser una prueba estadística extremadamente útil y poderosa; sin embargo, debe utilizarse adecuadamente. Es importante que las medidas utilizadas para evaluar el mediador y la variable dependiente sean teóricamente distintas y que la variable independiente y el mediador no puedan interactuar. Si hubiera una interacción entre la variable independiente y el mediador, habría motivos para investigar la moderación .

Otro modelo que se pone a prueba con frecuencia es aquel en el que las variables que compiten en el modelo son mediadores potenciales alternativos o una causa no medida de la variable dependiente. Una variable adicional en un modelo causal puede oscurecer o confundir la relación entre las variables independientes y dependientes. Los factores de confusión potenciales son variables que pueden tener un impacto causal tanto en la variable independiente como en la variable dependiente. Incluyen fuentes comunes de error de medición (como se explicó anteriormente), así como otras influencias compartidas por las variables independientes y dependientes.

En los estudios experimentales, existe una preocupación especial por los aspectos de la manipulación o el entorno experimental que pueden explicar los efectos del estudio, en lugar del factor teórico motivador. Cualquiera de estos problemas puede producir relaciones espurias entre las variables independientes y dependientes medidas. Ignorar una variable de confusión puede sesgar las estimaciones empíricas del efecto causal de la variable independiente.

Una variable supresora aumenta la validez predictiva de otra variable cuando se incluye en una ecuación de regresión. La supresión puede ocurrir cuando una sola variable causal está relacionada con una variable de resultado a través de dos variables mediadoras separadas, y cuando uno de esos efectos mediados es positivo y uno es negativo. En tal caso, cada variable mediadora suprime u oculta el efecto que se transmite a través de la otra variable mediadora. Por ejemplo, las puntuaciones de inteligencia más altas (una variable causal, A ) pueden causar un aumento en la detección de errores (una variable mediadora, B ) que a su vez puede causar una disminución de los errores cometidos en el trabajo en una línea de montaje (una variable de resultado, X ); al mismo tiempo, la inteligencia también podría causar un aumento en el aburrimiento ( C ), que a su vez puede causar un aumento de los errores ( X ). Por lo tanto, en una ruta causal, la inteligencia disminuye los errores, y en la otra los aumenta. Cuando no se incluye ninguno de los mediadores en el análisis, la inteligencia parece no tener efecto o un efecto débil sobre los errores. Sin embargo, cuando se controla el aburrimiento, la inteligencia parecerá disminuir los errores, y cuando se controla la detección de errores, la inteligencia parecerá aumentar los errores. Si se pudiera aumentar la inteligencia manteniendo constante únicamente el aburrimiento, los errores disminuirían; si se pudiera aumentar la inteligencia manteniendo constante únicamente la detección de errores, los errores aumentarían.

En general, la omisión de supresores o factores de confusión conducirá a una subestimación o una sobreestimación del efecto de A sobre X , reduciendo o inflando artificialmente la magnitud de una relación entre dos variables.

Otras terceras variables importantes son los moderadores . Los moderadores son variables que pueden hacer que la relación entre dos variables sea más fuerte o más débil. Dichas variables caracterizan aún más las interacciones en la regresión al afectar la dirección y/o la fuerza de la relación entre X e Y. Una relación moderadora puede considerarse como una interacción . Se produce cuando la relación entre las variables A y B depende del nivel de C. Consulte moderación para obtener más información.

La mediación y la moderación pueden coexistir en los modelos estadísticos. Es posible mediar la moderación y moderar la mediación.

La mediación moderada es cuando el efecto del tratamiento A sobre el mediador y/o el efecto parcial B sobre la variable dependiente dependen a su vez de los niveles de otra variable (moderador). Básicamente, en la mediación moderada, primero se establece la mediación y luego se investiga si el efecto de mediación que describe la relación entre la variable independiente y la variable dependiente está moderado por diferentes niveles de otra variable (es decir, un moderador). Esta definición ha sido esbozada por Muller, Judd y Yzerbyt (2005) ^[20] y Preacher, Rucker y Hayes (2007). ^[21]

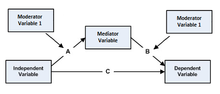
Hay cinco modelos posibles de mediación moderada, como se ilustra en los diagramas siguientes. ^[20]

1. En el primer modelo la variable independiente también modera la relación entre el mediador y la variable dependiente.
2. El segundo modelo posible de mediación moderada implica una nueva variable que modera la relación entre la variable independiente y el mediador (la ruta A ).
3. El tercer modelo de mediación moderada implica una nueva variable moderadora que modera la relación entre el mediador y la variable dependiente (la ruta B ).
4. La mediación moderada también puede ocurrir cuando una variable moderadora afecta tanto la relación entre la variable independiente y el mediador (la ruta A ) como la relación entre el mediador y la variable dependiente (la ruta B ).
5. El quinto y último modelo posible de mediación moderada implica dos nuevas variables moderadoras, una que modera la ruta A y la otra que modera la ruta B.

Además de los modelos mencionados anteriormente, también puede existir una nueva variable que modere la relación entre la variable independiente y el mediador (la ruta A) mientras que al mismo tiempo la nueva variable modera la relación entre la variable independiente y la variable dependiente (la ruta C). ^[1]

La moderación mediada es una variante tanto de la moderación como de la mediación. En este caso, inicialmente hay una moderación general y se media el efecto directo de la variable moderadora sobre el resultado. La principal diferencia entre la moderación mediada y la mediación moderada es que, en el caso de la primera, hay una moderación inicial (general) y este efecto se media, mientras que en el caso de la segunda no hay moderación, sino que se modera el efecto del tratamiento sobre el mediador (ruta A ) o el efecto del mediador sobre el resultado (ruta B ). ^[20]

Para establecer la moderación mediada, primero se debe establecer la moderación , lo que significa que la dirección y/o la fuerza de la relación entre las variables independientes y dependientes (camino C ) difieren dependiendo del nivel de una tercera variable (la variable moderadora). A continuación, los investigadores buscan la presencia de moderación mediada cuando tienen una razón teórica para creer que hay una cuarta variable que actúa como el mecanismo o proceso que causa la relación entre la variable independiente y la moderadora (camino A ) o entre el moderador y la variable dependiente (camino C ).

El siguiente es un ejemplo publicado de moderación mediada en la investigación psicológica. ^[22] A los participantes se les presentó un estímulo inicial (una inducción) que les hizo pensar en la moralidad o en el poder. Luego participaron en el Juego del Dilema del Prisionero (PDG), en el que los participantes simulan que ellos y su compañero en el crimen han sido arrestados, y deben decidir si permanecer leales a su compañero o competir con su compañero y cooperar con las autoridades. Los investigadores descubrieron que los individuos prosociales se vieron afectados por las inducciones de moralidad y poder, mientras que los individuos pro-yo no. Por lo tanto, la orientación al valor social (pro-yo vs. prosocial) moderó la relación entre la inducción (variable independiente: moralidad vs. poder) y el comportamiento elegido en el PDG (variable dependiente: competitivo vs. cooperativo).

Los investigadores buscaron luego la presencia de un efecto moderador mediado. Los análisis de regresión revelaron que el tipo de estímulo (moralidad vs. poder) mediaba la relación moderadora de la orientación de valores sociales de los participantes sobre el comportamiento de PDG. Los participantes prosociales que experimentaron el estímulo de moralidad esperaban que su pareja cooperara con ellos, por lo que ellos mismos eligieron cooperar. Los participantes prosociales que experimentaron el estímulo de poder esperaban que su pareja compitiera con ellos, lo que los hizo más propensos a competir con su pareja y cooperar con las autoridades. Por el contrario, los participantes con una orientación de valores sociales pro-yo siempre actuaron competitivamente.

Muller, Judd y Yzerbyt (2005) ^[20] describen tres modelos fundamentales que sustentan tanto la mediación moderada como la moderación mediada. Mo representa la(s) variable(s) moderadora(s), Me representa la(s) variable(s) mediadora(s) y ε _i representa el error de medición de cada ecuación de regresión.

Moderación de la relación entre la variable independiente (X) y la variable dependiente (Y), también llamada efecto general del tratamiento (ruta C en el diagrama).

${\displaystyle Y=\beta _{40}+\beta _{41}X+\beta _{42}Mo+\beta _{43}XMo+\varepsilon _{4}}$

• Para establecer una moderación general, el peso de la regresión β ₄₃ debe ser significativo (primer paso para establecer una moderación mediada).
• Para establecer una mediación moderada es necesario que no haya ningún efecto de moderación, por lo que el peso de la regresión β ₄₃ no debe ser significativo.

Moderación de la relación entre la variable independiente y el mediador (camino A ).

${\displaystyle Me=\beta _{50}+\beta _{51}X+\beta _{52}Mo+\beta _{53}XMo+\varepsilon _{5}}$

• Si el peso de la regresión β ₅₃ es significativo, el moderador afecta la relación entre la variable independiente y el mediador.

Moderación tanto de la relación entre las variables independientes y dependientes (ruta A ) como de la relación entre el mediador y la variable dependiente (ruta B ).

${\displaystyle Y=\beta _{60}+\beta _{61}X+\beta _{62}Mo+\beta _{63}XMo+\beta _{64}Me+\beta _{65}MeMo+\varepsilon _{6}}$

• Si tanto β ₅₃ en el paso 2 como β ₆₃ en el paso 3 son significativos, el moderador afecta la relación entre la variable independiente y el mediador (ruta A ).
• Si tanto β ₅₃ en el paso 2 como β ₆₅ en el paso 3 son significativos, el moderador afecta la relación entre el mediador y la variable dependiente (ruta B ).
• Una o ambas de las condiciones anteriores pueden ser verdaderas.

El análisis de mediación cuantifica el grado en que una variable participa en la transmisión del cambio de una causa a su efecto. Es inherentemente una noción causal, por lo que no puede definirse en términos estadísticos. Sin embargo, tradicionalmente la mayor parte del análisis de mediación se ha llevado a cabo dentro de los confines de la regresión lineal, con una terminología estadística que oculta el carácter causal de las relaciones involucradas. Esto ha dado lugar a dificultades, sesgos y limitaciones que se han aliviado con los métodos modernos de análisis causal, basados ​​en diagramas causales y lógica contrafactual.

La fuente de estas dificultades reside en definir la mediación en términos de cambios inducidos por la adición de una tercera variable a una ecuación de regresión. Esos cambios estadísticos son epifenómenos que a veces acompañan a la mediación pero que, en general, no logran captar las relaciones causales que el análisis de la mediación pretende cuantificar.

La premisa básica del enfoque causal es que no siempre es apropiado "controlar" al mediador M cuando buscamos estimar el efecto directo de X sobre Y (véase la Figura anterior). La lógica clásica para "controlar" por M es que, si logramos evitar que M cambie, entonces cualquier cambio que midamos en Y es atribuible únicamente a variaciones en X y entonces estamos justificados en proclamar el efecto observado como "efecto directo de X sobre Y ". Desafortunadamente, "controlar por M " no evita físicamente que M cambie; simplemente limita la atención del analista a los casos de valores M iguales . Además, el lenguaje de la teoría de la probabilidad no posee la notación para expresar la idea de "evitar que M cambie" o "mantener físicamente M constante". El único operador que proporciona la probabilidad es "Condicionamiento", que es lo que hacemos cuando "controlamos" por M , o agregamos M como regresor en la ecuación para Y. El resultado es que, en lugar de mantener físicamente M constante (digamos en M = m ) y comparar Y para unidades bajo X  = 1' con aquellas bajo X = 0, permitimos que M varíe pero ignoramos todas las unidades excepto aquellas en las que M alcanza el valor M  =  m . Estas dos operaciones son fundamentalmente diferentes y producen resultados diferentes. ^{[23] [24]} excepto en el caso de que no se omitan variables. Los efectos mediados por un condicionamiento inadecuado pueden ser un tipo de mal control .

Para ilustrar esto, supongamos que los términos de error de M e Y están correlacionados. En tales condiciones, el coeficiente estructural B y A (entre M e Y y entre Y y X ) ya no se puede estimar mediante la regresión de Y sobre X y M . De hecho, las pendientes de regresión pueden ser ambas distintas de cero incluso cuando C es cero. ^[25] Esto tiene dos consecuencias. En primer lugar, se deben idear nuevas estrategias para estimar los coeficientes estructurales A, B y C . En segundo lugar, las definiciones básicas de los efectos directos e indirectos deben ir más allá del análisis de regresión y deben invocar una operación que imite la "fijación de M ", en lugar del "condicionamiento sobre M ".

Un operador de este tipo, denominado do( M  =  m ), fue definido en Pearl (1994) ^[24] y opera eliminando la ecuación de M y reemplazándola por una constante m . Por ejemplo, si el modelo de mediación básico consta de las ecuaciones:

${\displaystyle X=f(\varepsilon _{1}),~~M=g(X,\varepsilon _{2}),~~Y=h(X,M,\varepsilon _{3}),}$

Luego, después de aplicar el operador do( M  =  m ) el modelo se convierte en:

${\displaystyle X=f(\varepsilon _{1}),~~M=m,~~Y=h(X,m,\varepsilon _{3})}$

y después de aplicar el operador do( X  =  x ) el modelo se convierte en:

${\displaystyle X=x,M=g(x,\varepsilon _{2}),Y=h(x,M,\varepsilon _{3})}$

donde las funciones f y g , así como las distribuciones de los términos de error ε ₁ y ε ₃ permanecen inalteradas. Si renombramos además las variables M e Y resultantes de do( X  =  x ) como M ( x ) e Y ( x ), respectivamente, obtenemos lo que llegó a conocerse como "resultados potenciales" ^[26] o "contrafácticos estructurales". ^[27] Estas nuevas variables proporcionan una notación conveniente para definir efectos directos e indirectos. En particular, se han definido cuatro tipos de efectos para la transición de X  = 0 a X  = 1:

(a) Efecto total –

${\displaystyle TE=E[Y(1)-Y(0)]}$

(b) Efecto directo controlado -

${\displaystyle CDE(m)=E[Y(1,m)-Y(0,m)]}$

(c) Efecto directo natural -

${\displaystyle NDE=E[Y(1,M(0))-Y(0,M(0))]}$

(d) Efecto indirecto natural

${\displaystyle NIE=E[Y(0,M(1))-Y(0,M(0))]}$

Donde E [ ] representa la expectativa tomada sobre los términos de error.

Estos efectos tienen las siguientes interpretaciones:

• TE mide el aumento esperado en el resultado Y a medida que X cambia de X=0 a X =1 , mientras que al mediador se le permite rastrear el cambio en X según lo dicta la función M = g(X, ε ₂ ) .
• La CDE mide el aumento esperado en el resultado Y a medida que X cambia de X = 0 a X = 1, mientras que el mediador se fija en un nivel preestablecido M = m de manera uniforme en toda la población.
• La NDE mide el aumento esperado en Y a medida que X cambia de X = 0 a X = 1, mientras fija la variable mediadora en cualquier valor que hubiera obtenido bajo X = 0, es decir, antes del cambio.
• NIE mide el aumento esperado en Y cuando X se mantiene constante, en X = 1, y M cambia a cualquier valor que hubiera alcanzado (para cada individuo) bajo X = 1.
• La diferencia TE-NDE mide hasta qué punto la mediación es necesaria para explicar el efecto, mientras que la NIE mide hasta qué punto la mediación es suficiente para sostenerlo.

No existe una versión controlada del efecto indirecto porque no hay manera de desactivar el efecto directo fijando una variable a una constante.

Según estas definiciones el efecto total puede descomponerse como una suma

${\displaystyle TE=NDE-NIE_{r}}$

donde NIE _r representa la transición inversa, de X  = 1 a X = 0; se vuelve aditiva en sistemas lineales, donde la inversión de las transiciones implica inversión de signo.

El poder de estas definiciones reside en su generalidad: son aplicables a modelos con interacciones no lineales arbitrarias, dependencias arbitrarias entre las perturbaciones y variables tanto continuas como categóricas.

En el análisis lineal, todos los efectos se determinan mediante sumas de productos de coeficientes estructurales, dando

${\displaystyle {\begin{aligned}TE&=C+AB\\CDE(m)&=NDE=C,{\text{ independent of }}m\\NIE&=AB.\end{aligned}}}$

Por lo tanto, todos los efectos son estimables siempre que se identifique el modelo. En sistemas no lineales, se necesitan condiciones más estrictas para estimar los efectos directos e indirectos. ^{[9] [28] [29]} Por ejemplo, si no existe confusión (es decir, ε ₁ , ε ₂ y ε ₃ son mutuamente independientes), se pueden derivar las siguientes fórmulas: ^[9]

${\displaystyle {\begin{aligned}TE&=E(Y\mid X=1)-E(Y\mid X=0)\\CDE(m)&=E(Y\mid X=1,M=m)-E(Y\mid X=0,M=m)\\NDE&=\sum _{m}[E(Y|X=1,M=m)-E(Y\mid X=0,M=m)]P(M=m\mid X=0)\\NIE&=\sum _{m}[P(M=m\mid X=1)-P(M=m\mid X=0)]E(Y\mid X=0,M=m).\end{aligned}}}$

Las dos últimas ecuaciones se denominan Fórmulas de Mediación ^{[30] [31] [32]} y se han convertido en el objetivo de estimación en muchos estudios de mediación. ^{[28] [29] [31] [32]} Proporcionan expresiones libres de distribución para efectos directos e indirectos y demuestran que, a pesar de la naturaleza arbitraria de las distribuciones de error y las funciones f , g y h , los efectos mediados pueden estimarse a partir de datos utilizando regresión. Los análisis de mediación moderada y moderadores mediadores caen como casos especiales del análisis de mediación causal, y las fórmulas de mediación identifican cómo los diversos coeficientes de interacción contribuyen a los componentes necesarios y suficientes de la mediación. ^{[29] [30]}

Supongamos que el modelo toma la forma

${\displaystyle {\begin{aligned}X&=\varepsilon _{1}\\M&=b_{0}+b_{1}X+\varepsilon _{2}\\Y&=c_{0}+c_{1}X+c_{2}M+c_{3}XM+\varepsilon _{3}\end{aligned}}}$

donde el parámetro cuantifica el grado en que M modifica el efecto de X sobre Y . Incluso cuando todos los parámetros se estiman a partir de los datos, todavía no es obvio qué combinaciones de parámetros miden el efecto directo e indirecto de X sobre Y , o, de manera más práctica, cómo evaluar la fracción del efecto total que se explica por la mediación y la fracción que se debe a la mediación. En el análisis lineal, la primera fracción se captura por el producto , la segunda por la diferencia , y las dos cantidades coinciden. Sin embargo, en presencia de interacción, cada fracción exige un análisis separado, como lo dicta la Fórmula de Mediación, que produce:${\displaystyle c_{3}}$${\displaystyle TE}$${\displaystyle TE}$${\displaystyle b_{1}c_{2}/TE}$${\displaystyle (TE-c_{1})/TE}$

${\displaystyle {\begin{aligned}NDE&=c_{1}+b_{0}c_{3}\\NIE&=b_{1}c_{2}\\TE&=c_{1}+b_{0}c_{3}+b_{1}(c_{2}+c_{3})\\&=NDE+NIE+b_{1}c_{3}.\end{aligned}}}$

Por lo tanto, la fracción de respuesta de salida para la que la mediación sería suficiente es

${\displaystyle {\frac {NIE}{TE}}={\frac {b_{1}c_{2}}{c_{1}+b_{0}c_{3}+b_{1}(c_{2}+c_{3})}},}$

mientras que la fracción para la cual sería necesaria la mediación es

${\displaystyle 1-{\frac {NDE}{TE}}={\frac {b_{1}(c_{2}+c_{3})}{c_{1}+b_{0}c_{3}+b_{1}(c_{2}+c_{3})}}.}$

Estas fracciones implican combinaciones no obvias de los parámetros del modelo y pueden construirse mecánicamente con la ayuda de la Fórmula de Mediación. Es significativo que, debido a la interacción, un efecto directo puede mantenerse incluso cuando el parámetro desaparece y, además, un efecto total puede mantenerse incluso cuando desaparecen tanto los efectos directos como los indirectos. Esto ilustra que la estimación de parámetros de forma aislada nos dice poco sobre el efecto de la mediación y, de manera más general, la mediación y la moderación están entrelazadas y no pueden evaluarse por separado.${\displaystyle c_{1}}$

A partir del 19 de junio de 2014, este artículo se deriva total o parcialmente de Causal Analysis in Theory and Practice . El titular de los derechos de autor ha autorizado el contenido de manera que permita su reutilización bajo CC BY-SA 3.0 y GFDL . Se deben respetar todos los términos pertinentes. ^{[ enlace roto ‍ ]}

Notas

Bibliografía

• Preacher, Kristopher J.; Hayes, Andrew F. (2004). "Procedimientos de SPSS y SAS para estimar efectos indirectos en modelos de mediación simples". Métodos, instrumentos y computadoras de investigación del comportamiento . 36 (4): 717–731. doi : 10.3758/BF03206553 . hdl : 1808/1491 . PMID  15641418.
• Preacher, Kristopher J.; Hayes, Andrew F. (2008). "Estrategias asintóticas y de remuestreo para evaluar y comparar efectos indirectos en modelos de múltiples mediadores". Métodos de investigación del comportamiento . 40 (3): 879–891. doi : 10.3758/BRM.40.3.879 . PMID  18697684.
• Preacher, KJ; Zyphur, MJ; Zhang, Z. (2010). "Un marco general multinivel SEM para evaluar la mediación multinivel". Psychological Methods . 15 (3): 209–233. CiteSeerX  10.1.1.570.7747 . doi :10.1037/a0020141. PMID  20822249.
• Baron, RM y Kenny, DA (1986) "La distinción entre variables moderador-mediador en la investigación psicológica social: consideraciones conceptuales, estratégicas y estadísticas", Journal of Personality and Social Psychology , vol. 51(6), págs. 1173-1182.
• Cohen, J. (1988). Análisis de potencia estadística para las ciencias del comportamiento (2.ª ed.). Nueva York, NY: Academic Press.
• Hayes, AF (2009). "Más allá de Baron y Kenny: análisis de mediación estadística en el nuevo milenio". Communication Monographs . 76 (4): 408–420. doi :10.1080/03637750903310360. S2CID  53599087.
• Howell, DC (2009). Métodos estadísticos para psicología (7.ª ed.). Belmot, CA: Cengage Learning.
• MacKinnon, DP; Lockwood, CM (2003). "Avances en métodos estadísticos para la investigación de la prevención del abuso de sustancias". Prevention Science . 4 (3): 155–171. doi :10.1023/A:1024649822872. PMC  2843515 . PMID  12940467.
• Preacher, KJ; Kelley, K. (2011). "Medidas de tamaño de efecto para modelos de mediación: estrategias cuantitativas para comunicar efectos indirectos". Psychological Methods . 16 (2): 93–115. doi :10.1037/a0022658. PMID  21500915.
• Rucker, DD, Preacher, KJ, Tormala, ZL y Petty, RE (2011). "Análisis de mediación en psicología social: prácticas actuales y nuevas recomendaciones". Social and Personality Psychology Compass , 5/6, 359–371.
• Sobel, ME (1982). "Intervalos de confianza asintóticos para efectos indirectos en modelos de ecuaciones estructurales". Metodología sociológica . 13 : 290–312. doi :10.2307/270723. JSTOR  270723.
• Spencer, SJ; Zanna, MP; Fong, GT (2005). "Establecer una cadena causal: por qué los experimentos suelen ser más eficaces que los análisis mediacionales a la hora de examinar los procesos psicológicos". Journal of Personality and Social Psychology . 89 (6): 845–851. doi :10.1037/0022-3514.89.6.845. PMID  16393019.
• Pearl, Judea (2012). "La fórmula de mediación: una guía para la evaluación de vías causales en modelos no lineales". En Berzuini, C.; Dawid, P.; Bernardinelli, L. (eds.). Causalidad: perspectivas y aplicaciones estadísticas . Chichester, Reino Unido: John Wiley and Sons, Ltd., págs. 151–179.
• Shaughnessy JJ, Zechmeister E. y Zechmeister J. (2006). Métodos de investigación en psicología (7.ª ed., págs. 51-52). Nueva York: McGraw Hill.
• Tolman, EC (1938). "Los determinantes del comportamiento en un punto de elección". Psychological Review . 45 : 1–41. doi :10.1037/h0062733.
• Tolman, EC; Honzik, CH (1930). "Grados de hambre, recompensa y falta de recompensa, y aprendizaje en laberintos en ratas". Publicaciones de la Universidad de California en Psicología . 4 : 241–275.
• Vanderweele, Tyler J. (2015). Explicación en inferencia causal .

• Resumen de los métodos de mediación en PsychWiki Archivado el 15 de julio de 2011 en Wayback Machine.
• Ejemplo de mediación causal utilizando puntuaciones de propensión The Methodology Center, Penn State University
• Libro sobre análisis de moderación y mediación, que incluye una introducción a la macro PROCESS para SPSS y SAS Andrew F. Hayes, Universidad Estatal de Ohio
• Texto en línea de "El determinante de la conducta en un punto de elección"
• Kenneth MacCorquodale y Paul E. Meehl (1948) SOBRE UNA DISTINCIÓN ENTRE CONSTRUCCIONES HIPOTÉTICAS Y VARIABLES INTERVENTORAS Clásicos en la Historia de la Psicología , retr. 22 de agosto de 2011.