- La evolución temporal de la función de onda clásica KvN para el potencial de Morse : . Los puntos negros son partículas clásicas que siguen la ley de movimiento de Newton . Las líneas continuas representan el conjunto de niveles del hamiltoniano . Este vídeo ilustra la diferencia fundamental entre la mecánica KvN y la de Liouville.
- Contraparte cuántica de la propagación clásica KvN a la izquierda: la evolución temporal de la función de Wigner del potencial de Morse en unidades atómicas (UA). Las líneas continuas representan el conjunto de niveles del hamiltoniano subyacente . Nótese que se utiliza la misma condición inicial para esta propagación cuántica y para la propagación KvN a la izquierda.
Mecánica clásica de Koopman-von Neumann
| Parte de una serie sobre |
| Mecánica clásica |
|---|
La teoría de Koopman-von Neumann (KvN) es una descripción de la mecánica clásica como una teoría operacional similar a la mecánica cuántica , basada en un espacio de Hilbert de funciones de onda complejas e integrables al cuadrado . Como sugiere su nombre, la teoría KvN está vagamente relacionada con el trabajo de Bernard Koopman y John von Neumann en 1931 y 1932, respectivamente. [1] [2] [3] Sin embargo, como se explica en esta entrada, los orígenes históricos de la teoría y su nombre son complicados.
Historia
La mecánica estadística describe los sistemas macroscópicos en términos de conjuntos estadísticos , como las propiedades macroscópicas de un gas ideal . La teoría ergódica es una rama de las matemáticas que surge del estudio de la mecánica estadística.
Teoría ergódica
Los orígenes de la teoría de Koopman-von Neumann están estrechamente relacionados con el surgimiento [ ¿cuándo? ] de la teoría ergódica como rama independiente de las matemáticas, en particular con la hipótesis ergódica de Boltzmann .
En 1931, Koopman y André Weil [ cita requerida ] observaron de forma independiente que el espacio de fases del sistema clásico se puede convertir en un espacio de Hilbert. Según esta formulación, las funciones que representan observables físicos se convierten en vectores, con un producto interno definido en términos de una regla de integración natural sobre la densidad de probabilidad del sistema en el espacio de fases. Esta reformulación permite extraer conclusiones interesantes sobre la evolución de los observables físicos a partir del teorema de Stone , que se había demostrado poco antes. Este hallazgo inspiró a von Neumann a aplicar el nuevo formalismo al problema ergódico. Posteriormente, publicó varios resultados seminales en la teoría ergódica moderna, incluida la prueba de su teorema ergódico medio .
Atribución histórica errónea
La teoría de Koopman-von Neumann se utiliza a menudo hoy en día para referirse a una reformulación de la mecánica clásica en la que la densidad de probabilidad de un sistema clásico en el espacio de fases se expresa en términos de una función de onda subyacente, lo que significa que los vectores del espacio de Hilbert clásico son funciones de onda, en lugar de observables físicos.
Este enfoque no se originó con Koopman o von Neumann, para quienes el espacio de Hilbert clásico consistía en observables físicos, en lugar de funciones de onda. De hecho, como señalaron en 1961 Thomas F. Jordan y EC George Sudarshan :
Koopman demostró cómo las transformaciones dinámicas de la mecánica clásica, consideradas como transformaciones que preservan la medida del espacio de fases, inducen transformaciones unitarias en el espacio de Hilbert de funciones que son integrables al cuadrado con respecto a una función de densidad en el espacio de fases. Esta formulación del espacio de Hilbert de la mecánica clásica fue desarrollada posteriormente por von Neumann. Cabe señalar que este espacio de Hilbert no corresponde al espacio de vectores de estado de la mecánica cuántica, sino al espacio de Hilbert de operadores en los vectores de estado (eligiendo la traza del producto de dos operadores como el producto escalar). [4]
La práctica de expresar distribuciones de probabilidad clásicas en el espacio de fases en términos de funciones de onda subyacentes se remonta al menos al trabajo de 1952-1953 de Mário Schenberg sobre mecánica estadística. [5] [6] Este método fue desarrollado independientemente varias veces más, por Angelo Loinger en 1962, [7] por Giacomo Della Riccia y Norbert Wiener en 1966, [8] y por el propio EC George Sudarshan en 1976. [9]
El nombre "teoría de Koopman-von Neumann" para representar sistemas clásicos basados en espacios de Hilbert compuestos por funciones de onda clásicas es, por tanto, un ejemplo de la ley de epónimo de Stigler . Esta atribución errónea parece haber aparecido por primera vez en un artículo de Danilo Mauro en 2002. [10]
Definición y dinámica
Derivación a partir de la ecuación de Liouville
En el enfoque de Koopman y von Neumann (KvN), la dinámica en el espacio de fases se describe mediante una densidad de probabilidad (clásica), recuperada de una función de onda subyacente –la función de onda de Koopman–von Neumann– como el cuadrado de su valor absoluto (más precisamente, como la amplitud multiplicada por su propio conjugado complejo ). Esto es análogo a la regla de Born en mecánica cuántica. En el marco KvN, los observables se representan mediante operadores autoadjuntos conmutativos que actúan sobre el espacio de Hilbert de las funciones de onda KvN. La conmutatividad implica físicamente que todos los observables son medibles simultáneamente. Contraste esto con la mecánica cuántica, donde los observables no necesitan conmutar, lo que subraya el principio de incertidumbre , el teorema de Kochen–Specker y las desigualdades de Bell . [11]
Se postula que la función de onda KvN evoluciona exactamente según la misma ecuación de Liouville que la densidad de probabilidad clásica. A partir de este postulado se puede demostrar que, efectivamente, se recupera la dinámica de la densidad de probabilidad.
En la mecánica estadística clásica, la densidad de probabilidad (con respecto a la medida de Liouville ) obedece a la ecuación de Liouville [12] [13] con el liouvilliano autoadjunto donde denota el hamiltoniano clásico (es decir, el liouvilliano es multiplicado por el campo vectorial hamiltoniano considerado como un operador diferencial de primer orden). La misma ecuación dinámica se postula para la función de onda KvN, por lo tanto , y para su conjugado complejo. De ello se sigue utilizando la regla del producto que demuestra que la dinámica de la densidad de probabilidad se puede recuperar a partir de la función de onda KvN.
- Observación
- El último paso de esta derivación se basa en el operador de Liouville clásico que contiene solo derivadas de primer orden en la coordenada y el momento; este no es el caso de la mecánica cuántica, donde la ecuación de Schrödinger contiene derivadas de segundo orden.
[12] [13]
Derivación a partir de axiomas de operadores
Por el contrario, es posible partir de postulados de operadores, similares a los axiomas del espacio de Hilbert de la mecánica cuántica , y derivar la ecuación de movimiento especificando cómo evolucionan los valores esperados. [14]
Los axiomas relevantes son que, como en la mecánica cuántica (i) los estados de un sistema están representados por vectores normalizados de un espacio de Hilbert complejo, y los observables están dados por operadores autoadjuntos que actúan en ese espacio, (ii) el valor esperado de un observable se obtiene de la misma manera que el valor esperado en la mecánica cuántica , (iii) las probabilidades de medir ciertos valores de algunos observables se calculan mediante la regla de Born , y (iv) el espacio de estados de un sistema compuesto es el producto tensorial de los espacios del subsistema.
Los axiomas anteriores (i) a (iv), con el producto interno escrito en notación entre corchetes , son
- ,
- El valor esperado de un observable en el tiempo es
- La probabilidad de que una medición de un observable en el tiempo dé como resultado es , donde . (Este axioma es un análogo de la regla de Born en mecánica cuántica. [15] )
- (ver Producto tensorial de los espacios de Hilbert ).
Estos axiomas nos permiten recuperar el formalismo tanto de la mecánica clásica como de la cuántica. [14] En concreto, bajo el supuesto de que los operadores clásicos de posición y momento conmutan , la ecuación de Liouville para la función de onda KvN se recupera a partir de las leyes de movimiento de Newton promediadas . Sin embargo, si la coordenada y el momento obedecen a la relación de conmutación canónica , se obtiene la ecuación de Schrödinger de la mecánica cuántica.
Partimos de las siguientes ecuaciones para los valores esperados de la coordenada x y el momento p
También conocidas como leyes de Newton del movimiento promediadas sobre el conjunto. Con la ayuda de los axiomas del operador, se pueden reescribir como
Observe una estrecha similitud con los teoremas de Ehrenfest en mecánica cuántica. Las aplicaciones de la regla del producto conducen a
en el que sustituimos una consecuencia del teorema de Stone y obtenemos
Dado que estas identidades deben ser válidas para cualquier estado inicial, se puede descartar el promedio y se deriva el sistema de ecuaciones del conmutador para la incógnita.
| ( ecuaciones del conmutador para L ) |
Supongamos que la coordenada y el momento conmutan . Esta suposición significa físicamente que la coordenada y el momento de la partícula clásica se pueden medir simultáneamente, lo que implica la ausencia del principio de incertidumbre .
La solución no puede ser simplemente de la forma porque implicaría las contracciones y . Por lo tanto, debemos utilizar operadores adicionales y obedecer
| ( Álgebra KvN ) |
La necesidad de emplear estos operadores auxiliares surge porque todos los observables clásicos conmutan. Ahora buscamos en la forma . Utilizando el álgebra KvN , las ecuaciones del conmutador para L se pueden convertir en las siguientes ecuaciones diferenciales: [14] [16]
De donde concluimos que la función de onda KvN clásica evoluciona de acuerdo con la ecuación de movimiento tipo Schrödinger.
| ( ecuación dinámica KvN ) |
Demostremos explícitamente que la ecuación dinámica KvN es equivalente a la mecánica clásica de Liouville .
Dado que y conmutan, comparten los vectores propios comunes
| ( xp vector propio ) |
con la resolución de la identidad Entonces, se obtiene de la ecuación ( álgebra KvN ) Proyectando la ecuación ( ecuación dinámica KvN ) sobre , obtenemos la ecuación de movimiento para la función de onda KvN en la representación xp
| ( Ecuación dinámica KvN en XP ) |
La cantidad es la amplitud de probabilidad de que una partícula clásica se encuentre en un punto con momento en el tiempo . Según los axiomas anteriores, la densidad de probabilidad está dada por . Utilizando la identidad así como ( ecuación dinámica KvN en xp ), recuperamos la ecuación clásica de Liouville
| ( ecuación de Liouville ) |
Además, de acuerdo con los axiomas del operador y ( xp eigenvec ), Por lo tanto, la regla para calcular promedios de observables en la mecánica estadística clásica se ha recuperado de los axiomas del operador con el supuesto adicional . Como resultado, la fase de una función de onda clásica no contribuye a los promedios observables. Al contrario de la mecánica cuántica, la fase de una función de onda KvN es físicamente irrelevante. Por lo tanto, la inexistencia del experimento de doble rendija [13] [17] [18] así como el efecto Aharonov-Bohm [19] se establece en la mecánica KvN.
Proyectando la ecuación dinámica KvN sobre el vector propio común de los operadores y (es decir, -representación), se obtiene la mecánica clásica en el espacio de configuración duplicada, [20] cuya generalización conduce [20] [21] [22] [23] [24] a la formulación del espacio de fases de la mecánica cuántica .
Al igual que en la derivación de la mecánica clásica, partimos de las siguientes ecuaciones para promedios de la coordenada x y el momento p
Con la ayuda de los axiomas del operador, se pueden reescribir como
Estos son los teoremas de Ehrenfest en mecánica cuántica. Las aplicaciones de la regla del producto conducen a
en el que sustituimos una consecuencia del teorema de Stone
donde se introdujo como una constante de normalización para equilibrar la dimensionalidad. Dado que estas identidades deben ser válidas para cualquier estado inicial, se puede descartar el promedio y se deriva el sistema de ecuaciones del conmutador para el generador cuántico de movimiento desconocido.
Al contrario de lo que ocurre en la mecánica clásica, suponemos que los observables de la coordenada y el momento obedecen a la relación de conmutación canónica . Si se establece , las ecuaciones del conmutador se pueden convertir en ecuaciones diferenciales [14] [16]
cuya solución es el familiar hamiltoniano cuántico
Por lo tanto, la ecuación de Schrödinger se derivó de los teoremas de Ehrenfest al suponer la relación de conmutación canónica entre la coordenada y el momento. Esta derivación, así como la derivación de la mecánica clásica KvN, muestra que la diferencia entre la mecánica cuántica y la clásica se reduce esencialmente al valor del conmutador .
Medidas
En la formulación del espacio de Hilbert y del operador de la mecánica clásica, la función de onda de Koopman von Neumann toma la forma de una superposición de estados propios, y la medición colapsa la función de onda KvN al estado propio que está asociado al resultado de la medición, en analogía con el colapso de la función de onda de la mecánica cuántica.
Sin embargo, se puede demostrar que para la mecánica clásica de Koopman-von Neumann las mediciones no selectivas dejan la función de onda KvN sin cambios. [12]
Mecánica de KvN vs Liouville
La ecuación dinámica KvN ( KvN dynamical eq in xp ) y la ecuación de Liouville ( Liouville eq ) son ecuaciones diferenciales parciales lineales de primer orden . Se recuperan las leyes de movimiento de Newton aplicando el método de características a cualquiera de estas ecuaciones. Por lo tanto, la diferencia clave entre la mecánica KvN y la de Liouville radica en la ponderación de las trayectorias individuales: en la mecánica KvN se pueden utilizar pesos arbitrarios, subyacentes a la función de onda clásica, mientras que en la mecánica de Liouville solo se permiten pesos positivos, que representan la densidad de probabilidad (véase este esquema).

Analogía cuántica
Al estar explícitamente basada en el lenguaje del espacio de Hilbert, la mecánica clásica KvN adopta muchas técnicas de la mecánica cuántica, por ejemplo, técnicas de perturbación y diagrama [25] así como métodos integrales funcionales . [26] [27] [28] El enfoque KvN es muy general y se ha extendido a sistemas disipativos , [29] mecánica relativista , [30] y teorías de campos clásicas . [14] [31] [32] [33]
El enfoque KvN es fructífero en estudios sobre la correspondencia cuántico-clásica [14] [15] [34] [35] [36] ya que revela que la formulación del espacio de Hilbert no es exclusivamente mecano-cuántica. [37] Incluso los espinores de Dirac no son excepcionalmente cuánticos ya que se utilizan en la generalización relativista de la mecánica KvN. [30] De manera similar a la formulación del espacio de fases más conocida de la mecánica cuántica, el enfoque KvN puede entenderse como un intento de llevar la mecánica clásica y cuántica a un marco matemático común. De hecho, la evolución temporal de la función de Wigner se aproxima, en el límite clásico, a la evolución temporal de la función de onda KvN de una partícula clásica. [30] [38] Sin embargo, una semejanza matemática con la mecánica cuántica no implica la presencia de efectos cuánticos distintivos. En particular, la imposibilidad del experimento de doble rendija [13] [17] [18] y el efecto Aharonov–Bohm [19] se demuestran explícitamente en el marco KvN.
Véase también
- Mecánica clásica
- Mecánica estadística
- Teorema de Liouville
- Mecánica cuántica
- Formulación del espacio de fases de la mecánica cuántica
- Distribución de cuasiprobabilidad de Wigner
- Sistemas dinámicos
- Teoría ergódica
Referencias
- ^ Koopman, BO (1931). "Sistemas hamiltonianos y transformaciones en el espacio de Hilbert". Actas de la Academia Nacional de Ciencias . 17 (5): 315–318. Bibcode :1931PNAS...17..315K. doi : 10.1073/pnas.17.5.315 . PMC 1076052 . PMID 16577368.
- ^ von Neumann, J. (1932). "Zur Operatorenmethode In Der Klassischen Mechanik". Anales de Matemáticas (en alemán). 33 (3): 587–642. doi :10.2307/1968537. JSTOR 1968537.
- ^ von Neumann, J. (1932). "Zusatze Zur Arbeit 'Zur Operadorenmethode...'". Anales de Matemáticas (en alemán). 33 (4): 789–791. doi :10.2307/1968225. JSTOR 1968225.
- ^ Jordan, Thomas F.; Sudarshan, ECG (1 de octubre de 1961). "Formalismo dinámico de grupos de Lie y la relación entre la mecánica cuántica y la mecánica clásica". Reseñas de física moderna . 33 (4): 515–524. doi :10.1103/RevModPhys.33.515.
- ^ Schönberg, M. (1952). "Aplicación de métodos de segunda cuantificación a la mecánica estadística clásica". Il Nuovo Cimento . 9 (12): 1139–1182. doi :10.1007/bf02782925. ISSN 0029-6341.
- ^ Schönberg, M. (1953). "Aplicación de métodos de segunda cuantificación a la mecánica estadística clásica (II)". Il Nuovo Cimento . 10 (4): 419–472. doi :10.1007/bf02781980. ISSN 0029-6341.
- ^ Loinger, A (1962). "Grupo de Galilei y ecuación de Liouville". Anales de Física . 20 (1): 132–144. doi :10.1016/0003-4916(62)90119-7. ISSN 0003-4916.
- ^ Riccia, Giacomo Della; Wiener, Norbert (1966-08-01). "Mecánica ondulatoria en el espacio de fases clásico, movimiento browniano y teoría cuántica". Revista de física matemática . 7 (8): 1372–1383. doi :10.1063/1.1705047. ISSN 0022-2488.
- ^ Sudarshan, ECG (1976). "Interacción entre sistemas clásicos y cuánticos y la medición de observables cuánticos". Pramana . 6 (3): 117–126. doi :10.1007/bf02847120. ISSN 0304-4289.
- ^ MAURO, D. (10 de abril de 2002). "SOBRE LAS ONDAS DE KOOPMAN–VON NEUMANN". Revista Internacional de Física Moderna A . 17 (9): 1301–1325. arXiv : quant-ph/0105112 . doi :10.1142/s0217751x02009680. ISSN 0217-751X.
- ^ Landau, LJ (1987). "Sobre la violación de la desigualdad de Bell en la teoría cuántica". Physics Letters A . 120 (2): 54–56. Bibcode :1987PhLA..120...54L. doi :10.1016/0375-9601(87)90075-2.
- ^ abc Mauro, D. (2002). "Temas de la teoría de Koopman-von Neumann". arXiv : quant-ph/0301172 .Tesis doctoral, Università degli Studi di Trieste.
- ^ abcd Mauro, D. (2002). "On Koopman–Von Neumann Waves". Revista Internacional de Física Moderna A . 17 (9): 1301–1325. arXiv : quant-ph/0105112 . Código Bibliográfico :2002IJMPA..17.1301M. CiteSeerX 10.1.1.252.9355 . doi :10.1142/S0217751X02009680. S2CID 14186986.
- ^ abcdef Bondar, D.; Cabrera, R.; Lompay, R.; Ivanov, M.; Rabitz, H. (2012). "Modelado dinámico operacional que trasciende la mecánica cuántica y clásica". Physical Review Letters . 109 (19): 190403. arXiv : 1105.4014 . Código Bibliográfico :2012PhRvL.109s0403B. doi :10.1103/PhysRevLett.109.190403. PMID 23215365. S2CID 19605000.
- ^ ab Brumer, P.; Gong, J. (2006). "Regla de nacimiento en mecánica cuántica y clásica". Physical Review A . 73 (5): 052109. arXiv : quant-ph/0604178 . Código Bibliográfico :2006PhRvA..73e2109B. doi :10.1103/PhysRevA.73.052109. hdl :1807/16870. S2CID 43054665.
- ^ ab Transtrum, MK; Van Huele, JFOS (2005). "Relaciones de conmutación para funciones de operadores". Journal of Mathematical Physics . 46 (6): 063510. Bibcode :2005JMP....46f3510T. doi :10.1063/1.1924703. S2CID 15429665.
- ^ ab Gozzi, E.; Mauro, D. (2004). "Sobre Koopman-Von Neumann Waves Ii". Revista Internacional de Física Moderna A. 19 (9): 1475. arXiv : quant-ph/0306029 . Código Bib : 2004IJMPA..19.1475G. CiteSeerX 10.1.1.252.1596 . doi :10.1142/S0217751X04017872. S2CID 6448720.
- ^ ab Gozzi, E.; Pagani, C. (2010). "Simetrías locales universales y no superposición en mecánica clásica". Physical Review Letters . 105 (15): 150604. arXiv : 1006.3029 . Código Bibliográfico :2010PhRvL.105o0604G. doi :10.1103/PhysRevLett.105.150604. PMID 21230883. S2CID 8531262.
- ^ ab Gozzi, E.; Mauro, D. (2002). "Acoplamiento mínimo en la teoría de Koopman–von Neumann". Anales de Física . 296 (2): 152–186. arXiv : quant-ph/0105113 . Código Bibliográfico :2002AnPhy.296..152G. CiteSeerX 10.1.1.252.9506 . doi :10.1006/aphy.2001.6206. S2CID 14952718.
- ^ ab Blokhintsev, DI (1977). "Física estadística clásica y mecánica cuántica". Física soviética Uspekhi . 20 (8): 683–690. Código Bibliográfico :1977SvPhU..20..683B. doi :10.1070/PU1977v020n08ABEH005457.
- ^ Blokhintsev, DI (1940). "El conjunto cuántico de Gibbs y su conexión con el conjunto clásico". J. Phys. URSS . 2 (1): 71–74.
- ^ Blokhintsev, DI; Nemirovsky, P (1940). "Conexión del conjunto cuántico con el conjunto clásico de Gibbs. II". J. Phys. URSS . 3 (3): 191–194.
- ^ Blokhintsev, DI; Dadyshevsky, Ya. B. (1941). "Sobre la separación de un sistema en partes cuánticas y clásicas". Zh. Eksp. Teor. Fiz . 11 (2–3): 222–225.
- ^ Blokhintsev, DI (2010). La filosofía de la mecánica cuántica . Springer. ISBN 9789048183357.
- ^ Liboff, RL (2003). Teoría cinética: descripciones clásicas, cuánticas y relativistas . Springer. ISBN 9780387955513.
- ^ Gozzi, E. (1988). "Invariancia BRS oculta en mecánica clásica". Physics Letters B . 201 (4): 525–528. Código Bibliográfico :1988PhLB..201..525G. doi :10.1016/0370-2693(88)90611-9.
- ^ Gozzi, E.; Reuter, M.; Thacker, W. (1989). "Invariancia oculta de BRS en mecánica clásica. II". Physical Review D . 40 (10): 3363–3377. Bibcode :1989PhRvD..40.3363G. doi :10.1103/PhysRevD.40.3363. PMID 10011704.
- ^ Blasone, M.; Jizba, P.; Kleinert, H. (2005). "Enfoque de la integral de trayectorias para la derivación de 't Hooft de la física cuántica a partir de la física clásica". Physical Review A . 71 (5): 052507. arXiv : quant-ph/0409021 . Código Bibliográfico :2005PhRvA..71e2507B. doi :10.1103/PhysRevA.71.052507. S2CID 2571677.
- ^ Chruściński, D. (2006). "El enfoque de Koopman sobre la disipación". Informes sobre física matemática . 57 (3): 319–332. Bibcode :2006RpMP...57..319C. doi :10.1016/S0034-4877(06)80023-6.
- ^ abc Renan Cabrera; Bondar; Rabitz (2011). "Función de Wigner relativista y límite clásico consistente para partículas de espín 1/2". arXiv : 1107.5139 [quant-ph].
- ^ Carta, P.; Gozzi, E.; Mauro, D. (2006). "Formulación de Koopman-von Neumann de las teorías clásicas de Yang-Mills: I". Annalen der Physik . 15 (3): 177–215. arXiv : hep-th/0508244 . Código Bib : 2006AnP...518..177C. doi : 10.1002/andp.200510177. S2CID 11500710.
- ^ Gozzi, E.; Penco, R. (2011). "Tres aproximaciones a la teoría clásica del campo térmico". Anales de Física . 326 (4): 876–910. arXiv : 1008.5135 . Código Bibliográfico :2011AnPhy.326..876G. doi :10.1016/j.aop.2010.11.018. S2CID 118666414.
- ^ Cattaruzza, E.; Gozzi, E.; Francisco Neto, A. (2011). "Diagrama de la teoría de campos escalares clásica". Anales de Física . 326 (9): 2377–2430. arXiv : 1010.0818 . Código bibliográfico : 2011AnPhy.326.2377C. CiteSeerX 10.1.1.750.8350 . doi :10.1016/j.aop.2011.05.009. S2CID 73523322.
- ^ Wilkie, J.; Brumer, P. (1997). "Correspondencia cuántico-clásica a través de la dinámica de Liouville. I. Sistemas integrables y descomposición espectral caótica". Physical Review A . 55 (1): 27–42. arXiv : chao-dyn/9608013 . Bibcode :1997PhRvA..55...27W. doi :10.1103/PhysRevA.55.27. hdl :1807/16867. S2CID 18553588.
- ^ Wilkie, J.; Brumer, P. (1997). "Correspondencia cuántico-clásica a través de la dinámica de Liouville. II. Correspondencia para sistemas hamiltonianos caóticos". Physical Review A . 55 (1): 43–61. arXiv : chao-dyn/9608014 . Código Bibliográfico :1997PhRvA..55...43W. doi :10.1103/PhysRevA.55.43. hdl :1807/16874. S2CID 15116232.
- ^ Abrikosov, AA; Gozzi, E.; Mauro, D. (2005). "Descuantificación geométrica". Anales de Física . 317 (1): 24–71. arXiv : quant-ph/0406028 . Código Bibliográfico :2005AnPhy.317...24A. doi :10.1016/j.aop.2004.12.001. S2CID 18876047.
- ^ Bracken, AJ (2003). "La mecánica cuántica como aproximación a la mecánica clásica en el espacio de Hilbert", Journal of Physics A: Mathematical and General , 36 (23), L329.
- ^ Bondar; Renan Cabrera; Zhdanov; Rabitz (2013). "Desmitificación de la negatividad de la función de Wigner". Physical Review A . 88 (5): 263. arXiv : 1202.3628 . Código Bibliográfico :2013PhRvA..88e2108B. doi :10.1103/PhysRevA.88.052108. S2CID 119155284.
Lectura adicional
- Mauro, D. (2002). "Temas de la teoría de Koopman-von Neumann". arXiv : quant-ph/0301172 .Tesis doctoral, Università degli Studi di Trieste.
- HR Jauslin, D. Sugny, Dinámica de sistemas mixtos clásicos-cuánticos, cuantificación geométrica y estados coherentes [ vínculo muerto permanente ] , Serie de notas de conferencias, IMS, NUS, Vol. de revisión, 13 de agosto de 2009
- El legado de John von Neumann (Actas de simposios sobre matemáticas puras, vol. 50), editado por James Glimm, John Impagliazzo e Isadore Singer . — Amata Graphics, 2006. — ISBN 0821842196
- U. Klein, De la teoría de Koopman-von Neumann a la teoría cuántica, Quantum Stud.: Math. Found. (2018) 5:219–227.[1]

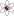






![{\displaystyle {\frac {\parcial }{\parcial t}}\psi (x,p,t)=\left[-{\frac {\parcial H(x,p)}{\parcial p}}{\frac {\parcial }{\parcial x}}+{\frac {\parcial H(x,p)}{\parcial x}}{\frac {\parcial }{\parcial p}}\right]\psi (x,p,t),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a0816d67ef80c599b5c30618439347abbe55cb6)
![{\displaystyle {\frac {\parcial }{\parcial t}}\psi ^{*}(x,p,t)=\left[-{\frac {\parcial H(x,p)}{\parcial p}}{\frac {\parcial }{\parcial x}}+{\frac {\parcial H(x,p)}{\parcial x}}{\frac {\parcial }{\parcial p}}\right]\psi ^{*}(x,p,t).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f63a58d04a1a9575bcea504c8ea8c3f96592cce)

![{\displaystyle {\frac {\parcial }{\parcial t}}\rho (x,p,t)=\left[-{\frac {\parcial H(x,p)}{\parcial p}}{\frac {\parcial }{\parcial x}}+{\frac {\parcial H(x,p)}{\parcial x}}{\frac {\parcial }{\parcial p}}\right]\rho (x,p,t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/836d603fb65bcc183dd9517832d009860ad25fd4)











![{\displaystyle {\begin{aligned}im\langle \Psi (t)|[{\hat {L}},{\hat {x}}]|\Psi (t)\rangle &=\langle \Psi ( t)|{\hat {p}}|\Psi (t)\rangle ,\\i\langle \Psi (t)|[{\hat {L}},{\hat {p}}]|\Psi (t)\rangle &=-\langle \Psi (t)|U'({\hat {x}})|\Psi (t)\rangle .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf562fe3f4f533464e7e44d9206859914ffc6419)

![{\displaystyle im[{\hat {L}},{\hat {x}}]={\hat {p}},\qquad i[{\hat {L}},{\hat {p}}]=-U'({\hat {x}}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3fa526671b181e6f86037186dac4fbbc42309ad)
![{\displaystyle [{\hat {x}},{\hat {p}}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14612aab25c12572e2a278b14296b88b203aaa58)

![{\displaystyle estoy[L({\hat {x}},{\hat {p}}),{\hat {x}}]=0={\hat {p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d1b2afa360c33dee6b6724c7b6d7fbe23540e92)
![{\displaystyle i[L({\hat {x}},{\hat {p}}),{\hat {p}}]=0=-U'({\hat {x}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09ad8b1b4bb9afe6e97ca62a88c800add1d13f2b)


![{\displaystyle [{\hat {x}},{\hat {\lambda }}_{x}]=[{\hat {p}},{\hat {\lambda }}_{p}]=i,\quad [{\hat {x}},{\hat {p}}]=[{\hat {x}},{\hat {\lambda }}_{p}]=[{\hat {p}},{\hat {\lambda }}_{x}]=[{\hat {\lambda }}_{x},{\hat {\lambda }}_{p}]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3fa3783cf8b4cf54eb22d0320d36f89500cce220)










![{\displaystyle \left[{\frac {\parcial }{\parcial t}}+{\frac {p}{m}}{\frac {\parcial }{\parcial x}}-U'(x){\frac {\parcial }{\parcial p}}\right]\langle x,p|\Psi (t)\rangle =0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15fe77fcd8830da76f39306a7830767b03f26edf)





![{\displaystyle \left[{\frac {\parcial }{\parcial t}}+{\frac {p}{m}}{\frac {\parcial }{\parcial x}}-U'(x){\frac {\parcial }{\parcial p}}\right]\rho (x,p;t)=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adb5daaf112a7474e95e6e6fc5a97ea0b1066988)







![{\displaystyle estoy[{\sombrero {H}},{\sombrero {x}}]=\hbar {\sombrero {p}},\qquad i[{\sombrero {H}},{\sombrero {p} }]=-\hbar U'({\hat {x}}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d8ce0a590c88a8b4b034f50884fe0fa55a7223f)
![{\displaystyle [{\hat {x}},{\hat {p}}]=i\hbar }](https://wikimedia.org/api/rest_v1/media/math/render/svg/42dbbd0db710385288536bcf4f4a1b7cceb75d9a)



![{\displaystyle [{\hat {x}},{\hat {p}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16a78ed0f28b85cee5d3d3d835367b0a508acb80)


