Ley de Hubble

Parte de una serie sobre
Cosmología física
Big Bang  · Universo Edad del universo Cronología del universo
Universo primitivo Inflación  · Nucleosíntesis Antecedentes Onda gravitacional (GWB) Microondas (CMB)  · Neutrinos (CNB)
Expansión  · Futuro Ley de Hubble  · Desplazamiento al rojo Expansión del universo Métrica FLRW  · Ecuaciones de Friedmann Cosmología no homogénea El futuro de un universo en expansión El destino final del universo
Componentes  · Estructura Componentes Modelo Lambda-CDM Energía oscura  · Materia oscura Estructura Forma del universo Filamento galáctico  · Formación de galaxias Gran grupo de cuásares Estructura a gran escala Reionización  · Formación de estructuras
Experimentos Iniciativa Agujero Negro (BHI) Bumerang Explorador del fondo cósmico (COBE) Encuesta sobre energía oscura Observatorio espacial Planck Estudio del cielo digital de Sloan (SDSS) Estudio del corrimiento al rojo de galaxias 2dF ("2dF") Sonda de anisotropía de microondas de Wilkinson (WMAP)
Científicos Aaronson Alfven Alfer Copérnico De Sitter Polla Síndrome de Ehlers Einstein Ellis Friedman Galileo Gamow Guth Halcones El telescopio Hubble Huygens Kepler Lemaître Matemática Newton Penrose Penzias Rubin Schmidt Suave Suntzeff Sunyaev Tolmán Wilson Zeldovich Lista de cosmólogos
Historial del tema Descubrimiento de la radiación de fondo cósmico de microondas Historia de la teoría del Big Bang Cronología de las teorías cosmológicas
Categoría Portal de astronomía
en a mi

La ley de Hubble , también conocida como ley de Hubble-Lemaître , ^[1] es la observación en cosmología física de que las galaxias se alejan de la Tierra a velocidades proporcionales a su distancia. En otras palabras, cuanto más lejos están, más rápido se alejan. Para este propósito, la velocidad de recesión de una galaxia se determina típicamente midiendo el corrimiento al rojo , un cambio en la luz que emite hacia el extremo rojo del espectro de luz visible . El descubrimiento de la ley de Hubble se atribuye al trabajo publicado por Edwin Hubble en 1929. ^[2]

La ley de Hubble se considera la primera base observacional para la expansión del universo , y hoy sirve como una de las piezas de evidencia más citadas en apoyo del modelo del Big Bang . ^{[3] [4]} El movimiento de los objetos astronómicos debido únicamente a esta expansión se conoce como flujo de Hubble . ^[5] Se describe mediante la ecuación v = H ₀ D , con H ₀ la constante de proporcionalidad —la constante de Hubble— entre la "distancia propia" D a una galaxia (que puede cambiar con el tiempo, a diferencia de la distancia comóvil ) y su velocidad de separación v , es decir, la derivada de la distancia propia con respecto a la coordenada de tiempo cósmico . (Véase Distancias comovintes y propias § Usos de la distancia propia para una discusión de las sutilezas de esta definición de velocidad. )

La constante de Hubble se expresa con mayor frecuencia en km / s / Mpc , lo que da como resultado la velocidad de una galaxia a 1 megaparsec (3,09 × 10 ¹⁹  km) de distancia, que es de 70 km/s . Simplificando las unidades de la forma generalizada, se revela que H ₀ especifica una frecuencia (unidad del SI: s ⁻¹ ), lo que hace que el recíproco de H ₀ se conozca como el tiempo de Hubble (14 400 millones de años).

La constante de Hubble también puede expresarse como una tasa relativa de expansión. En esta forma H ₀  = 7%/ Gyr , lo que significa que al ritmo actual de expansión, una estructura no ligada tarda mil millones de años en crecer un 7%.

Aunque ampliamente atribuida a Edwin Hubble , ^{[6] [7] [8]} la noción de que el universo se expande a una tasa calculable fue derivada por primera vez de las ecuaciones de la relatividad general en 1922 por Alexander Friedmann . Friedmann publicó un conjunto de ecuaciones, ahora conocidas como las ecuaciones de Friedmann , que mostraban que el universo podría estar expandiéndose y presentaban la velocidad de expansión si ese fuera el caso. ^[9] Antes de Hubble, el astrónomo alemán Carl Wilhelm Wirtz , en dos publicaciones que datan de 1922 ^[10] y 1924, ^[11] ya había deducido con sus propios datos que las galaxias que parecían más pequeñas y tenues tenían mayores corrimientos al rojo y, por lo tanto, que las galaxias más distantes se alejan más rápido del observador. Luego, Georges Lemaître , en un artículo de 1927, dedujo independientemente que el universo podría estar expandiéndose, observó la proporcionalidad entre la velocidad de recesión y la distancia a los cuerpos distantes, y sugirió un valor estimado para la constante de proporcionalidad; Esta constante, cuando Edwin Hubble confirmó la existencia de la expansión cósmica y determinó un valor más preciso para ella dos años después, llegó a ser conocida por su nombre como la constante de Hubble. ^{[3] [12] [13] [14] [2]} Hubble infirió la velocidad de recesión de los objetos a partir de sus corrimientos al rojo , muchos de los cuales fueron medidos anteriormente y relacionados con la velocidad por Vesto Slipher en 1917. ^{[15] [16] [17]} La ​​combinación de las velocidades de Slipher con los cálculos y la metodología de distancia intergaláctica de Henrietta Swan Leavitt le permitió a Hubble calcular mejor una tasa de expansión para el universo. ^[18]

Aunque la constante de Hubble H ₀ es constante en cualquier momento dado en el tiempo, el parámetro de Hubble H , del cual la constante de Hubble es el valor actual, varía con el tiempo, por lo que el término constante a veces se considera un nombre inapropiado. ^{[19] [20]}

Una década antes de que Hubble hiciera sus observaciones, varios físicos y matemáticos habían establecido una teoría consistente de un universo en expansión utilizando las ecuaciones de campo de Einstein de la relatividad general . La aplicación de los principios más generales a la naturaleza del universo produjo una solución dinámica que entraba en conflicto con la noción entonces prevaleciente de un universo estático .

En 1912, Vesto M. Slipher midió el primer desplazamiento Doppler de una " nebulosa espiral " (el término obsoleto para las galaxias espirales) y pronto descubrió que casi todas esas nebulosas se alejaban de la Tierra. No comprendió las implicaciones cosmológicas de este hecho y, de hecho, en ese momento era muy controvertido si estas nebulosas eran o no "universos isla" fuera de la Vía Láctea. ^{[22] [23]}

En 1922, Alexander Friedmann derivó sus ecuaciones de Friedmann a partir de las ecuaciones de campo de Einstein , mostrando que el universo podría expandirse a una tasa calculable por las ecuaciones. ^[24] El parámetro utilizado por Friedmann se conoce hoy como el factor de escala y puede considerarse como una forma invariante de escala de la constante de proporcionalidad de la ley de Hubble. Georges Lemaître encontró de forma independiente una solución similar en su artículo de 1927 analizado en la siguiente sección. Las ecuaciones de Friedmann se derivan insertando la métrica para un universo homogéneo e isótropo en las ecuaciones de campo de Einstein para un fluido con una densidad y presión dadas . Esta idea de un espacio-tiempo en expansión eventualmente conduciría a las teorías del Big Bang y del estado estacionario de la cosmología.

En 1927, dos años antes de que Hubble publicara su propio artículo, el sacerdote y astrónomo belga Georges Lemaître fue el primero en publicar una investigación que derivó lo que hoy se conoce como la ley de Hubble. Según el astrónomo canadiense Sidney van den Bergh , "el descubrimiento de 1927 de la expansión del universo por parte de Lemaître fue publicado en francés en una revista de bajo impacto. En la traducción al inglés de alto impacto de 1931 de este artículo, se cambió una ecuación crítica omitiendo la referencia a lo que ahora se conoce como la constante de Hubble". ^[25] Ahora se sabe que las alteraciones en el artículo traducido fueron realizadas por el propio Lemaître. ^{[13] [26]}

Antes de la llegada de la cosmología moderna, se hablaba mucho sobre el tamaño y la forma del universo . En 1920, se produjo el debate Shapley-Curtis entre Harlow Shapley y Heber D. Curtis sobre esta cuestión. Shapley defendía la existencia de un universo pequeño, del tamaño de la Vía Láctea, y Curtis sostenía que el universo era mucho más grande. La cuestión se resolvió en la década siguiente con las observaciones mejoradas del Hubble.

Edwin Hubble realizó la mayor parte de su trabajo de observación astronómica profesional en el Observatorio del Monte Wilson , ^[27] que albergaba el telescopio más potente del mundo en ese momento. Sus observaciones de estrellas variables cefeidas en "nebulosas espirales" le permitieron calcular las distancias a estos objetos. Sorprendentemente, se descubrió que estos objetos estaban a distancias que los colocaban muy fuera de la Vía Láctea. Continuaron llamándose nebulosas y solo gradualmente el término galaxias lo reemplazó.

Los parámetros que aparecen en la ley de Hubble, velocidades y distancias, no se miden directamente. En realidad, determinamos, por ejemplo, el brillo de una supernova, lo que proporciona información sobre su distancia, y el corrimiento al rojo z = ∆ λ / λ de su espectro de radiación. Hubble correlacionó el brillo y el parámetro z .

Combinando sus mediciones de distancias entre galaxias con las mediciones de los corrimientos al rojo asociados a las galaxias realizadas por Vesto Slipher y Milton Humason , Hubble descubrió una proporcionalidad aproximada entre el corrimiento al rojo de un objeto y su distancia. Aunque había una dispersión considerable (que ahora se sabe que es causada por velocidades peculiares ; el "flujo de Hubble" se utiliza para referirse a la región del espacio lo suficientemente alejada como para que la velocidad de recesión sea mayor que las velocidades peculiares locales), Hubble pudo trazar una línea de tendencia a partir de las 46 galaxias que estudió y obtener un valor para la constante de Hubble de 500 (km/s)/Mpc (mucho más alto que el valor actualmente aceptado debido a errores en sus calibraciones de distancia; véase la escala de distancias cósmicas para más detalles). ^[31]

La ley de Hubble se puede representar fácilmente en un "diagrama de Hubble" en el que se representa gráficamente la velocidad (que se supone aproximadamente proporcional al corrimiento al rojo) de un objeto con respecto a su distancia del observador. ^[32] Una línea recta de pendiente positiva en este diagrama es la representación visual de la ley de Hubble.

Después de que se publicara el descubrimiento de Hubble, Albert Einstein abandonó su trabajo sobre la constante cosmológica , un término que había insertado en sus ecuaciones de relatividad general para obligarlas a producir la solución estática que previamente consideraba el estado correcto del universo. Las ecuaciones de Einstein en su forma más simple modelan un universo en expansión o en contracción, por lo que Einstein introdujo la constante para contrarrestar la expansión o la contracción y conducir a un universo estático y plano. ^[33] Después del descubrimiento de Hubble de que el universo estaba, de hecho, en expansión, Einstein calificó su suposición errónea de que el universo es estático como su "mayor error". ^[33] Por sí sola, la relatividad general podía predecir la expansión del universo, que (a través de observaciones como la curvatura de la luz por grandes masas o la precesión de la órbita de Mercurio ) podía observarse experimentalmente y compararse con sus cálculos teóricos utilizando soluciones particulares de las ecuaciones que había formulado originalmente.

En 1931, Einstein fue al Observatorio del Monte Wilson para agradecer a Hubble por proporcionar la base observacional para la cosmología moderna. ^[34]

La constante cosmológica ha recuperado atención en las últimas décadas como explicación hipotética de la energía oscura . ^[35]

El descubrimiento de la relación lineal entre el corrimiento al rojo y la distancia, junto con una supuesta relación lineal entre la velocidad de recesión y el corrimiento al rojo, produce una expresión matemática sencilla para la ley de Hubble, como sigue:

$${\displaystyle v=H_{0}\,D}$$

dónde

• v es la velocidad de recesión, normalmente expresada en km/s.
• H ₀ es la constante de Hubble y corresponde al valor de H (a menudo denominado parámetro de Hubble , que es un valor que depende del tiempo y que puede expresarse en términos del factor de escala ) en las ecuaciones de Friedmann tomadas en el momento de la observación denotado por el subíndice 0. Este valor es el mismo en todo el universo para un tiempo comóvil dado .
• D es la distancia propia (que puede cambiar con el tiempo, a diferencia de la distancia comóvil , que es constante) desde la galaxia hasta el observador, medida en megaparsecs ( Mpc ), en el espacio tridimensional definido por el tiempo cosmológico dado . (La velocidad de recesión es simplemente v = dD/dt ).

La ley de Hubble se considera una relación fundamental entre la velocidad de recesión y la distancia. Sin embargo, la relación entre la velocidad de recesión y el corrimiento al rojo depende del modelo cosmológico adoptado y no se establece excepto para pequeños corrimientos al rojo.

Para distancias D mayores que el radio de la esfera de Hubble r _HS , los objetos se alejan a una velocidad mayor que la de la luz ( ver Usos de la distancia adecuada para un análisis del significado de esto):

$${\displaystyle r_{\text{HS}}={\frac {c}{H_{0}}}\ .}$$

Como la "constante" de Hubble es una constante sólo en el espacio, no en el tiempo, el radio de la esfera de Hubble puede aumentar o disminuir en varios intervalos de tiempo. El subíndice "0" indica el valor de la constante de Hubble en la actualidad. ^[28] La evidencia actual sugiere que la expansión del universo se está acelerando ( ver Universo en aceleración ), lo que significa que para cualquier galaxia dada, la velocidad de recesión dD/dt aumenta con el tiempo a medida que la galaxia se mueve a distancias cada vez mayores; sin embargo, se cree que el parámetro de Hubble en realidad disminuye con el tiempo, lo que significa que si miráramos una distancia fija D y viéramos una serie de galaxias diferentes pasar esa distancia, las galaxias posteriores pasarían esa distancia a una velocidad menor que las anteriores. ^[37]

El corrimiento al rojo se puede medir determinando la longitud de onda de una transición conocida, como las líneas α del hidrógeno para cuásares distantes, y hallando el corrimiento fraccional en comparación con una referencia estacionaria. Por lo tanto, el corrimiento al rojo es una cantidad inequívoca para la observación experimental. La relación del corrimiento al rojo con la velocidad de recesión es otra cuestión. ^[38]

El corrimiento al rojo z se describe a menudo como una velocidad de corrimiento al rojo , que es la velocidad de recesión que produciría el mismo corrimiento al rojo si fuera causado por un efecto Doppler lineal (que, sin embargo, no es el caso, ya que el corrimiento es causado en parte por una expansión cosmológica del espacio , y porque las velocidades involucradas son demasiado grandes para usar una fórmula no relativista para el corrimiento Doppler). Esta velocidad de corrimiento al rojo puede superar fácilmente la velocidad de la luz. ^[39] En otras palabras, para determinar la velocidad de corrimiento al rojo v _rs , la relación:

$${\displaystyle v_{\text{rs}}\equiv cz,}$$

Se utiliza ^{[40] [41]} Es decir, no existe una diferencia fundamental entre la velocidad de corrimiento al rojo y el corrimiento al rojo: son rígidamente proporcionales y no están relacionadas por ningún razonamiento teórico. La motivación detrás de la terminología de "velocidad de corrimiento al rojo" es que la velocidad de corrimiento al rojo concuerda con la velocidad de una simplificación de baja velocidad de la llamada fórmula de Fizeau-Doppler ^[42]

$${\displaystyle z={\frac {\lambda _{\text{o}}}{\lambda _{\text{e}}}}-1={\sqrt {\frac {1+{\frac {v}{c}}}{1-{\frac {v}{c}}}}}-1\approx {\frac {v}{c}}.}$$

Aquí, λ _o , λ _e son las longitudes de onda observadas y emitidas respectivamente. Sin embargo, la "velocidad de corrimiento al rojo" v _rs no está tan simplemente relacionada con la velocidad real a velocidades mayores, y esta terminología conduce a confusión si se interpreta como una velocidad real. A continuación, se analiza la conexión entre el corrimiento al rojo o la velocidad de corrimiento al rojo y la velocidad recesional. ^[43]

Supongamos que R ( t ) se denomina factor de escala del universo y aumenta a medida que el universo se expande de una manera que depende del modelo cosmológico seleccionado. Esto significa que todas las distancias propias medidas D ( t ) entre puntos que se mueven conjuntamente aumentan proporcionalmente a R . (Los puntos que se mueven conjuntamente no se mueven entre sí excepto como resultado de la expansión del espacio). En otras palabras:

$${\displaystyle {\frac {D(t)}{D(t_{0})}}={\frac {R(t)}{R(t_{0})}},}$$

donde t ₀ es un tiempo de referencia. ^[44] Si la luz se emite desde una galaxia en el tiempo t _e y la recibimos en t ₀ , se desplaza hacia el rojo debido a la expansión del espacio, y este desplazamiento hacia el rojo z es simplemente:

$${\displaystyle z={\frac {R(t_{0})}{R(t_{\text{e}})}}-1.}$$

Supongamos que una galaxia está a una distancia D y que esta distancia cambia con el tiempo a una velocidad d _t D . A esta velocidad de recesión la llamamos "velocidad de recesión" v _r :

$${\displaystyle v_{\text{r}}=d_{t}D={\frac {d_{t}R}{R}}D.}$$

Ahora definimos la constante de Hubble como

$${\displaystyle H\equiv {\frac {d_{t}R}{R}},}$$

y descubre la ley de Hubble:

$${\displaystyle v_{\text{r}}=HD.}$$

Desde esta perspectiva, la ley de Hubble es una relación fundamental entre (i) la velocidad de recesión aportada por la expansión del espacio y (ii) la distancia a un objeto; la conexión entre el corrimiento al rojo y la distancia es una muleta utilizada para conectar la ley de Hubble con las observaciones. Esta ley se puede relacionar con el corrimiento al rojo z aproximadamente haciendo una expansión en serie de Taylor :

$${\displaystyle z={\frac {R(t_{0})}{R(t_{e})}}-1\approx {\frac {R(t_{0})}{R(t_{0})\left(1+(t_{e}-t_{0})H(t_{0})\right)}}-1\approx (t_{0}-t_{e})H(t_{0}),}$$

Si la distancia no es demasiado grande, todas las demás complicaciones del modelo se convierten en pequeñas correcciones, y el intervalo de tiempo es simplemente la distancia dividida por la velocidad de la luz:

$${\displaystyle z\approx (t_{0}-t_{\text{e}})H(t_{0})\approx {\frac {D}{c}}H(t_{0}),}$$

o

$${\displaystyle cz\approx DH(t_{0})=v_{r}.}$$

Según este enfoque, la relación cz = v _r es una aproximación válida para corrimientos al rojo bajos, que se puede reemplazar por una relación para corrimientos al rojo grandes que depende del modelo. Véase la figura de velocidad-corrimiento al rojo.

Estrictamente hablando, ni v ni D en la fórmula son directamente observables, porque son propiedades actuales de una galaxia, mientras que nuestras observaciones se refieren a la galaxia en el pasado, en el momento en que la luz que vemos actualmente la abandonó.

Para galaxias relativamente cercanas (con un corrimiento al rojo z mucho menor que uno), v y D no habrán cambiado mucho, y v puede estimarse utilizando la fórmula v = zc , donde c es la velocidad de la luz. Esto da la relación empírica encontrada por Hubble.

En el caso de galaxias distantes, v (o D ) no se puede calcular a partir de z sin especificar un modelo detallado de cómo cambia H con el tiempo. El corrimiento al rojo ni siquiera está directamente relacionado con la velocidad de recesión en el momento en que salió la luz, pero tiene una interpretación sencilla: (1 + z ) es el factor por el cual el universo se ha expandido mientras el fotón viajaba hacia el observador.

Al utilizar la ley de Hubble para determinar distancias, solo se puede utilizar la velocidad debida a la expansión del universo. Dado que las galaxias que interactúan gravitacionalmente se mueven entre sí independientemente de la expansión del universo, ^[45] estas velocidades relativas, llamadas velocidades peculiares, deben tenerse en cuenta en la aplicación de la ley de Hubble. Tales velocidades peculiares dan lugar a distorsiones del espacio de corrimiento al rojo .

El parámetro H se denomina comúnmente "constante de Hubble", pero es un nombre inapropiado, ya que es constante en el espacio sólo en un tiempo fijo; varía con el tiempo en casi todos los modelos cosmológicos, y todas las observaciones de objetos muy distantes son también observaciones del pasado distante, cuando la "constante" tenía un valor diferente. "Parámetro de Hubble" es un término más correcto, donde H ₀ denota el valor actual.

Otra fuente común de confusión es que el universo en aceleración no implica que el parámetro de Hubble esté en realidad aumentando con el tiempo; dado que en la mayoría de los modelos de aceleración, H aumenta relativamente más rápido que H, por lo que H disminuye con el tiempo. (La velocidad de recesión de una galaxia elegida sí aumenta, pero las diferentes galaxias que pasan por una esfera de radio fijo cruzan la esfera más lentamente en momentos posteriores).${\displaystyle H(t)\equiv {\dot {a}}(t)/a(t)}$${\displaystyle a}$${\displaystyle {\dot {a}}}$

Al definir el parámetro de desaceleración adimensional , se deduce que${\textstyle q\equiv -{\frac {{\ddot {a}}\,a}{{\dot {a}}^{2}}}}$

$${\displaystyle {\frac {dH}{dt}}=-H^{2}(1+q)}$$

De esto se desprende que el parámetro de Hubble disminuye con el tiempo, a menos que q < -1 ; esto último sólo puede ocurrir si el universo contiene energía fantasma , considerada teóricamente algo improbable.

Sin embargo, en el modelo estándar de materia oscura fría Lambda (modelo Lambda-CDM o ΛCDM), q tenderá a −1 desde arriba en el futuro distante a medida que la constante cosmológica se vuelve cada vez más dominante sobre la materia; esto implica que H se acercará desde arriba a un valor constante de ≈ 57 (km/s)/Mpc, y el factor de escala del universo crecerá entonces exponencialmente en el tiempo.

La derivación matemática de una ley de Hubble idealizada para un universo en expansión uniforme es un teorema bastante elemental de geometría en un espacio de coordenadas cartesiano /newtoniano tridimensional , que, considerado como un espacio métrico , es completamente homogéneo e isótropo (las propiedades no varían con la ubicación o la dirección). En términos simples, el teorema es el siguiente:

Dos puntos cualesquiera que se alejen del origen, cada uno siguiendo líneas rectas y con una velocidad proporcional a la distancia desde el origen, se alejarán uno del otro con una velocidad proporcional a la distancia que los separa.

De hecho, esto se aplica a los espacios no cartesianos siempre que sean localmente homogéneos e isótropos, específicamente a los espacios curvados negativa y positivamente frecuentemente considerados como modelos cosmológicos (ver forma del universo ).

Una observación que se desprende de este teorema es que ver objetos alejarse de nosotros en la Tierra no es una indicación de que la Tierra esté cerca de un centro desde el cual se está produciendo la expansión, sino más bien que cada observador en un universo en expansión verá objetos alejándose de ellos.

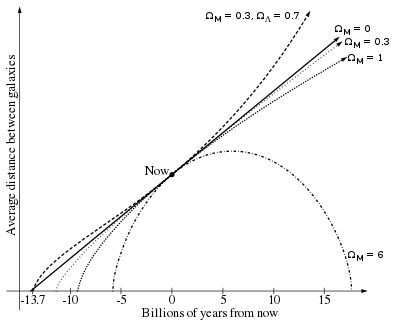
El valor del parámetro de Hubble cambia con el tiempo, aumentando o disminuyendo dependiendo del valor del llamado parámetro de desaceleración q , que se define por

$${\displaystyle q=-\left(1+{\frac {\dot {H}}{H^{2}}}\right).}$$

En un universo con un parámetro de desaceleración igual a cero, se deduce que H = 1/ t , donde t es el tiempo transcurrido desde el Big Bang. Un valor de q distinto de cero y dependiente del tiempo simplemente requiere la integración de las ecuaciones de Friedmann hacia atrás desde el tiempo presente hasta el momento en que el tamaño del horizonte comóvil era cero.

Durante mucho tiempo se creyó que q era positivo, lo que indicaba que la expansión se estaba desacelerando debido a la atracción gravitatoria. Esto implicaría una edad del universo menor que 1/ H (que son unos 14 mil millones de años). Por ejemplo, un valor para q de 1/2 (antes favorecido por la mayoría de los teóricos) daría la edad del universo como 2/(3 H ) . El descubrimiento en 1998 de que q es aparentemente negativo significa que el universo podría ser en realidad más antiguo que 1/ H . Sin embargo, las estimaciones de la edad del universo son muy cercanas a 1/ H .

La expansión del espacio resumida por la interpretación del Big Bang de la ley de Hubble es relevante para el viejo enigma conocido como la paradoja de Olbers : si el universo fuera infinito en tamaño, estático y lleno de una distribución uniforme de estrellas , entonces cada línea de visión en el cielo terminaría en una estrella, y el cielo sería tan brillante como la superficie de una estrella. Sin embargo, el cielo nocturno es en gran parte oscuro. ^{[46] [47]}

Desde el siglo XVII, los astrónomos y otros pensadores han propuesto muchas formas posibles de resolver esta paradoja, pero la solución actualmente aceptada depende en parte de la teoría del Big Bang y en parte de la expansión de Hubble: en un universo que existió durante un tiempo finito, solo la luz de un número finito de estrellas ha tenido tiempo suficiente para llegar hasta nosotros, y la paradoja se resuelve. Además, en un universo en expansión, los objetos distantes se alejan de nosotros, lo que hace que la luz que emanan de ellos se desplace hacia el rojo y disminuya su brillo cuando la vemos. ^{[46] [47]}

En lugar de trabajar con la constante de Hubble, una práctica común es introducir la constante adimensional de Hubble , usualmente denotada por h y comúnmente llamada "h pequeña", ^[31] y luego escribir la constante de Hubble H ₀ como h  × 100  km⋅ s ⁻¹ ⋅ Mpc ⁻¹ , toda la incertidumbre relativa del valor verdadero de H ₀ queda entonces relegada a h . ^[48] La constante adimensional de Hubble se usa a menudo cuando se dan distancias que se calculan a partir del corrimiento al rojo z usando la fórmula d ≈ ⁠do/H0_​⁠ × z . Como H ₀ no se conoce con precisión, la distancia se expresa como:

$${\displaystyle cz/H_{0}\approx (2998\times z){\text{ Mpc }}h^{-1}}$$

En otras palabras, se calcula 2998 ×  z y se dan las unidades como Mpc  h ^-1 o h ^-1  Mpc.

Ocasionalmente se puede elegir un valor de referencia distinto de 100, en cuyo caso se presenta un subíndice después de h para evitar confusiones; por ejemplo, h ₇₀ denota H ₀ = 70 h ₇₀  (km/s-1)/ Mpc , lo que implica h ₇₀ = h / 0,7 .

Esto no debe confundirse con el valor adimensional de la constante de Hubble, generalmente expresada en términos de unidades de Planck , obtenida al multiplicar H ₀ por1,75 × 10 ⁻⁶³ (de las definiciones de parsec y t _P ), por ejemplo para H ₀ = 70 , una versión de unidad de Planck deSe obtiene 1,2 × 10 ^{−61 .}

Un valor para q medido a partir de observaciones de velas estándar de supernovas de Tipo Ia , que se determinó en 1998 como negativo, sorprendió a muchos astrónomos con la implicación de que la expansión del universo actualmente se está "acelerando" ^[49] (aunque el factor de Hubble todavía está disminuyendo con el tiempo, como se mencionó anteriormente en la sección Interpretación; consulte los artículos sobre energía oscura y el modelo ΛCDM).

This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (March 2014) (Learn how and when to remove this message)

Comencemos con la ecuación de Friedmann :

$${\displaystyle H^{2}\equiv \left({\frac {\dot {a}}{a}}\right)^{2}={\frac {8\pi G}{3}}\rho -{\frac {kc^{2}}{a^{2}}}+{\frac {\Lambda c^{2}}{3}},}$$

donde H es el parámetro de Hubble, a es el factor de escala , G es la constante gravitacional , k es la curvatura espacial normalizada del universo e igual a −1, 0 o 1, y Λ es la constante cosmológica.

Si el universo está dominado por la materia , entonces la densidad de masa del universo ρ puede considerarse que incluye solo la materia, por lo que

$${\displaystyle \rho =\rho _{m}(a)={\frac {\rho _{m_{0}}}{a^{3}}},}$$

donde ρ _{m 0} es la densidad de la materia actual. A partir de la ecuación de Friedmann y los principios termodinámicos sabemos que, para las partículas no relativistas, su densidad de masa disminuye proporcionalmente al volumen inverso del universo, por lo que la ecuación anterior debe ser cierta. También podemos definir (ver parámetro de densidad para Ω _m )

$${\displaystyle {\begin{aligned}\rho _{c}&={\frac {3H_{0}^{2}}{8\pi G}};\\\Omega _{m}&\equiv {\frac {\rho _{m_{0}}}{\rho _{c}}}={\frac {8\pi G}{3H_{0}^{2}}}\rho _{m_{0}};\end{aligned}}}$$

por lo tanto:

$${\displaystyle \rho ={\frac {\rho _{c}\Omega _{m}}{a^{3}}}.}$$

Además, por definición,$${\displaystyle {\begin{aligned}\Omega _{k}&\equiv {\frac {-kc^{2}}{(a_{0}H_{0})^{2}}}\\\Omega _{\Lambda }&\equiv {\frac {\Lambda c^{2}}{3H_{0}^{2}}},\end{aligned}}}$$

donde el subíndice 0 se refiere a los valores actuales y a ₀ = 1. Sustituyendo todo esto en la ecuación de Friedmann al comienzo de esta sección y reemplazando a por a = 1/(1+ z ) se obtiene

$${\displaystyle H^{2}(z)=H_{0}^{2}\left(\Omega _{m}(1+z)^{3}+\Omega _{k}(1+z)^{2}+\Omega _{\Lambda }\right).}$$

Si el universo está dominado tanto por la materia como por la energía oscura, entonces la ecuación anterior para el parámetro de Hubble también será una función de la ecuación de estado de la energía oscura . Así que ahora:

$${\displaystyle \rho =\rho _{m}(a)+\rho _{de}(a),}$$

donde ρ _de es la densidad de masa de la energía oscura. Por definición, una ecuación de estado en cosmología es P = wρc ² , y si esto se sustituye en la ecuación de fluidos, que describe cómo evoluciona la densidad de masa del universo con el tiempo, entonces

$${\displaystyle {\begin{aligned}{\dot {\rho }}+3{\frac {\dot {a}}{a}}\left(\rho +{\frac {P}{c^{2}}}\right)=0;\\{\frac {d\rho }{\rho }}=-3{\frac {da}{a}}(1+w).\end{aligned}}}$$

Si w es constante, entonces

$${\displaystyle \ln {\rho }=-3(1+w)\ln {a};}$$

reticente:

$${\displaystyle \rho =a^{-3(1+w)}.}$$

Por lo tanto, para la energía oscura con una ecuación de estado constante w , . Si esto se sustituye en la ecuación de Friedman de manera similar a la anterior, pero esta vez se establece k = 0 , lo que supone un universo espacialmente plano, entonces (ver forma del universo )${\displaystyle \rho _{de}(a)=\rho _{de0}a^{-3(1+w)}}$

$${\displaystyle H^{2}(z)=H_{0}^{2}\left(\Omega _{m}(1+z)^{3}+\Omega _{de}(1+z)^{3(1+w)}\right).}$$

Si la energía oscura se deriva de una constante cosmológica como la introducida por Einstein, se puede demostrar que w = −1 . La ecuación se reduce entonces a la última ecuación en la sección del universo dominado por la materia, con Ω _k fijado en cero. En ese caso, la densidad de energía oscura inicial ρ _{de 0} viene dada por ^[50]

$${\displaystyle {\begin{aligned}\rho _{de0}&={\frac {\Lambda c^{2}}{8\pi G}}\,,\\\Omega _{de}&=\Omega _{\Lambda }.\end{aligned}}}$$

Si la energía oscura no tiene una ecuación de estado constante w , entonces

$${\displaystyle \rho _{de}(a)=\rho _{de0}e^{-3\int {\frac {da}{a}}\left(1+w(a)\right)},}$$

y para resolver esto, w ( a ) debe estar parametrizado, por ejemplo si w ( a ) = w ₀ + w _a (1− a ) , obteniendo ^[51]

$${\displaystyle H^{2}(z)=H_{0}^{2}\left(\Omega _{m}a^{-3}+\Omega _{de}a^{-3\left(1+w_{0}+w_{a}\right)}e^{-3w_{a}(1-a)}\right).}$$

Se han formulado otros ingredientes. ^{[52] [53] [54]}

This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (March 2014) (Learn how and when to remove this message)

La constante de Hubble H ₀ tiene unidades de tiempo inverso; el tiempo de Hubble t _H se define simplemente como el inverso de la constante de Hubble, ^[55] es decir

$${\displaystyle t_{H}\equiv {\frac {1}{H_{0}}}={\frac {1}{67.8\mathrm {~(km/s)/Mpc} }}=4.55\times 10^{17}\mathrm {~s} =14.4{\text{ billion years}}.}$$

Esto es ligeramente diferente de la edad del universo, que es de aproximadamente 13.800 millones de años. El tiempo de Hubble es la edad que habría tenido si la expansión hubiera sido lineal, ^[56] y es diferente de la edad real del universo porque la expansión no es lineal; depende del contenido de energía del universo (véase § Derivación del parámetro de Hubble).

Actualmente parece que nos estamos acercando a un período en el que la expansión del universo es exponencial debido al predominio creciente de la energía del vacío . En este régimen, el parámetro de Hubble es constante y el universo crece en un factor e cada tiempo de Hubble:

$${\displaystyle H\equiv {\frac {\dot {a}}{a}}={\textrm {constant}}\quad \Longrightarrow \quad a\propto e^{Ht}=e^{\frac {t}{t_{H}}}}$$

Del mismo modo, el valor generalmente aceptado de 2,27  Es ⁻¹ significa que (al ritmo actual) el universo crecería en un factor de e ^2,27 en un exasegundo .

Durante largos períodos de tiempo, la dinámica se complica por la relatividad general, la energía oscura, la inflación , etc., como se explicó anteriormente.

La longitud de Hubble o distancia de Hubble es una unidad de distancia en cosmología, definida como cH ⁻¹ —la velocidad de la luz multiplicada por el tiempo de Hubble—. Equivale a 4.420 millones de parsecs o 14.400 millones de años luz. (El valor numérico de la longitud de Hubble en años luz es, por definición, igual al del tiempo de Hubble en años). La distancia de Hubble sería la distancia entre la Tierra y las galaxias que actualmente se alejan de nosotros a la velocidad de la luz, como se puede ver sustituyendo D = cH ⁻¹ en la ecuación de la ley de Hubble, v = H ₀ D .

El volumen de Hubble se define a veces como un volumen del universo con un tamaño comóvil de cH ⁻¹ . La definición exacta varía: a veces se define como el volumen de una esfera con un radio de cH ⁻¹ , o alternativamente, un cubo de lado cH ⁻¹ . Algunos cosmólogos incluso usan el término volumen de Hubble para referirse al volumen del universo observable , aunque este tiene un radio aproximadamente tres veces mayor.

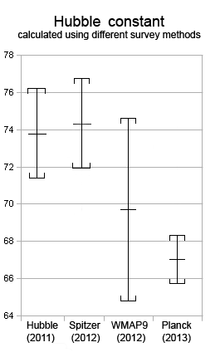
El valor de la constante de Hubble, H ₀ , indica la velocidad a la que se expande el universo. En 1929, Edwin Hubble determinó por primera vez que esta constante era500 km/s por millón de parsecs. Desde entonces, la constante de Hubble se ha medido activamente utilizando varios métodos. En los primeros tiempos, Hubble, por ejemplo, utilizó estrellas brillantes y la luz de la "nebulosa" para estimar el corrimiento al rojo y determinar la constante. Más tarde, después de que se descubriera que las supernovas de tipo Ia eran una " candela estándar " mejor para las galaxias distantes, se utilizaron las supernovas para determinar el corrimiento al rojo. Estas mediciones deben determinar primero la distancia de las estrellas o galaxias objetivo. Las incertidumbres en los supuestos físicos utilizados para determinar estas distancias han provocado estimaciones variables de la constante de Hubble. ^[3]

Más recientemente, los científicos utilizan mediciones del CMB (como los datos de Planck ) para determinar la constante de Hubble. El desafío de utilizar este método es que su resultado varía según los modelos cosmológicos utilizados. Debido a los diferentes valores de la constante de Hubble estimados utilizando diferentes técnicas, la determinación de la constante de Hubble es un campo de investigación activo (tensión de Hubble). La medición de alta precisión realizada con el telescopio espacial James Webb en 2023 ha confirmado la observación anterior del telescopio espacial Hubble , que dio una constante de Hubble de aproximadamente H ₀ = 74 (km/s)/Mpc . ^{[58] [59]}

La estimación original de Hubble de la constante que ahora lleva su nombre, basada en observaciones de estrellas variables Cefeidas como " velas estándar " para medir la distancia, ^[60] fue500 (km/s)/Mpc (mucho mayor que el valor que los astrónomos calculan actualmente). Observaciones posteriores del astrónomo Walter Baade le llevaron a darse cuenta de que había distintas " poblaciones " de estrellas (Población I y Población II) en una galaxia. Las mismas observaciones le llevaron a descubrir que hay dos tipos de estrellas variables cefeidas con diferentes luminosidades. Utilizando este descubrimiento, recalculó la constante de Hubble y el tamaño del universo conocido, duplicando el cálculo previo realizado por Hubble en 1929. ^{[61] [62] [60]} Anunció este hallazgo ante un asombro considerable en la reunión de 1952 de la Unión Astronómica Internacional en Roma.

Durante la mayor parte de la segunda mitad del siglo XX, el valor de H ₀ se estimó entre50 y 90 (km/s)/Mpc .

El valor de la constante de Hubble fue el tema de una larga y bastante amarga controversia entre Gérard de Vaucouleurs , quien afirmó que el valor estaba alrededor de 100, y Allan Sandage , quien afirmó que el valor estaba cerca de 50. ^[63] En una demostración de vitriolo compartida entre las partes, cuando Sandage y Gustav Andreas Tammann (colega de investigación de Sandage) reconocieron formalmente las deficiencias de confirmar el error sistemático de su método en 1975, Vaucouleurs respondió: "Es desafortunado que esta sobria advertencia fuera tan pronto olvidada e ignorada por la mayoría de los astrónomos y escritores de libros de texto". ^[64] En 1996, se llevó a cabo un debate moderado por John Bahcall entre Sidney van den Bergh y Gustav Tammann de manera similar al debate anterior de Shapley-Curtis sobre estos dos valores en competencia.

Esta variación previamente amplia en las estimaciones se resolvió parcialmente con la introducción del modelo ΛCDM del universo a fines de la década de 1990. La incorporación del modelo ΛCDM, las observaciones de cúmulos de alto corrimiento al rojo en longitudes de onda de rayos X y microondas utilizando el efecto Sunyaev–Zel'dovich , las mediciones de anisotropías en la radiación de fondo cósmico de microondas y los estudios ópticos dieron un valor de alrededor de 50–70 km/s/Mpc para la constante. ^[65]

En el siglo XXI, se han utilizado múltiples métodos para determinar la constante de Hubble. Las mediciones del "universo tardío" utilizando técnicas de escala de distancia calibrada han convergido en un valor de aproximadamente73 (km/s)/Mpc . Desde el año 2000, se dispone de técnicas de "universo temprano" basadas en mediciones del fondo cósmico de microondas , que coinciden en un valor cercano67,7 (km/s)/Mpc . ^[66] (Esto tiene en cuenta el cambio en la tasa de expansión desde el universo temprano, por lo que es comparable al primer número). Inicialmente, esta discrepancia estaba dentro de las incertidumbres de medición estimadas y, por lo tanto, no era motivo de preocupación. Sin embargo, a medida que las técnicas han mejorado, las incertidumbres de medición estimadas se han reducido, pero las discrepancias no , hasta el punto de que el desacuerdo ahora es altamente estadísticamente significativo . Esta discrepancia se llama "tensión de Hubble". ^{[67] [68]}

La causa de la tensión de Hubble es desconocida ^[69] y existen muchas posibles soluciones propuestas. La más conservadora es que existe un error sistemático desconocido que afecta a las observaciones del universo temprano o del universo tardío. Aunque intuitivamente atractiva, esta explicación requiere múltiples efectos no relacionados independientemente de si las observaciones del universo temprano o del universo tardío son incorrectas, y no hay candidatos obvios ^[68] . Además, cualquier error sistemático de este tipo tendría que afectar a múltiples instrumentos diferentes, ya que tanto las observaciones del universo temprano como las del universo tardío provienen de varios telescopios diferentes. ^{[a] [b]}

Otra posibilidad es que las observaciones sean correctas, pero que la discrepancia se deba a algún efecto no explicado. Si el principio cosmológico falla (véase el modelo Lambda-CDM § Violaciones del principio cosmológico ), entonces habría que revisar las interpretaciones existentes de la constante de Hubble y de la tensión de Hubble, lo que podría resolver la tensión de Hubble. ^[71] En particular, tendríamos que estar ubicados dentro de un vacío muy grande, de hasta un corrimiento al rojo de aproximadamente 0,5, para que dicha explicación no estuviera en tensión con las observaciones de supernovas y oscilaciones acústicas bariónicas . ^[68] Otra posibilidad es que se hayan subestimado las incertidumbres en las mediciones. ^[72]

Finalmente, otra posibilidad es una nueva física más allá del modelo cosmológico del universo actualmente aceptado, el modelo ΛCDM . ^{[68] [73]} Hay muchas teorías en esta categoría, por ejemplo, reemplazar la relatividad general con una teoría modificada de la gravedad podría resolver potencialmente la tensión, ^{[74] [75]} como puede hacerlo un componente de energía oscura en el universo temprano, ^{[c] [76] energía oscura con una} ecuación de estado variable en el tiempo , ^{[d] [77]} o materia oscura que se desintegra en radiación oscura. ^[78] Un problema al que se enfrentan todas estas teorías es que tanto las mediciones del universo temprano como del universo tardío dependen de múltiples líneas independientes de física, y es difícil modificar cualquiera de esas líneas mientras se preservan sus éxitos en otras partes. La escala del desafío se puede ver en cómo algunos autores han argumentado que la nueva física del universo temprano por sí sola no es suficiente; ^{[79] [80]} mientras que otros autores argumentan que la nueva física del universo tardío por sí sola tampoco es suficiente. ^[81] Sin embargo, los astrónomos están intentándolo, y el interés en la tensión de Hubble ha crecido fuertemente desde mediados de la década de 2010. ^[68]

Mediciones más recientes de la misión Planck publicadas en 2018 indican un valor más bajo de67,66 ± 0,42 (km/s)/Mpc , aunque, más recientemente, en marzo de 2019, se registró un valor superior deSe ha determinado 74,03 ± 1,42 (km/s)/Mpc utilizando un procedimiento mejorado que involucra al Telescopio Espacial Hubble. ^[82] Las dos mediciones difieren en el nivel de 4,4 σ , más allá de un nivel plausible de probabilidad. ^[83] La resolución de este desacuerdo es un área en curso de investigación activa. ^[84]

En octubre de 2018, los científicos presentaron una nueva tercera vía (dos métodos anteriores, uno basado en corrimientos al rojo y otro en la escala de distancias cósmicas, dieron resultados que no concuerdan), utilizando información de eventos de ondas gravitacionales (especialmente aquellos que involucran la fusión de estrellas de neutrones , como GW170817 ), para determinar la constante de Hubble. ^{[85] [86]}

En julio de 2019, los astrónomos informaron que se había propuesto un nuevo método para determinar la constante de Hubble y resolver la discrepancia de los métodos anteriores, basado en las fusiones de pares de estrellas de neutrones , tras la detección de la fusión de estrellas de neutrones de GW170817, un evento conocido como sirena oscura . ^{[87] [88]} Su medición de la constante de Hubble es73.3+5,3
-5,0(km/s)/Mpc. ^[89]

También en julio de 2019, los astrónomos informaron sobre otro nuevo método, que utiliza datos del telescopio espacial Hubble y se basa en distancias a estrellas gigantes rojas calculadas utilizando el indicador de distancia de la punta de la rama de las gigantes rojas (TRGB). Su medición de la constante de Hubble es69,8+1,9
-1,9 (km/s)/Mpc . ^{[90] [91] [92]}

En febrero de 2020, el Proyecto de Cosmología Megamaser publicó resultados independientes que confirmaron los resultados de la escala de distancias y diferían de los resultados del universo temprano en un nivel de significación estadística del 95%. ^[93] En julio de 2020, las mediciones de la radiación cósmica de fondo realizadas por el Telescopio de Cosmología de Atacama predicen que el Universo debería estar expandiéndose más lentamente de lo que se observa actualmente. ^[94]

En julio de 2023, se obtuvo una estimación independiente de la constante de Hubble a partir de la contraparte óptica de una fusión de estrellas de neutrones, una denominada kilonova . ^[95] Debido a la naturaleza de cuerpo negro de los espectros de kilonovas tempranas, ^[96] dichos sistemas proporcionan estimadores fuertemente restrictivos de la distancia cósmica. Utilizando la kilonova AT2017gfo, estas mediciones indican una estimación local de la constante de Hubble de67,0 ± 3,6 (km/s)/Mpc . ^{[97] [95]}

En agosto de 2024, Wendy Freedman et al. publicaron previamente una medición de la constante de Hubble utilizando datos del telescopio espacial James Webb para volver a medir el segundo peldaño de la escala de distancias cósmicas, utilizando estrellas de vela estándar para medir las distancias a diez galaxias cercanas que han albergado supernovas de tipo Ia , la vela estándar utilizada para el tercer peldaño. Utilizaron tres tipos diferentes de vela estándar: estrellas de la punta de la rama gigante roja, estrellas de la rama gigante asintótica de la región J ( estrellas de carbono particularmente brillantes en la banda J ) y las tradicionales estrellas variables cefeidas. ^{[98] [99] [100]} Las distancias TRGB y JAGB concordaron entre sí dentro del 1%, mientras que las distancias medidas por las cefeidas son un pequeño porcentaje más cortas, lo que da como resultado valores calculados de la constante de Hubble de69,85 ± 2,33 ,67,96 ± 2,65 , y72,05 ± 3,62 km/s/Mpc , respectivamente. Aunque aún no es concluyente, esto sugiere la posibilidad de que los valores más bajos de H ₀ puedan ser correctos y que las mediciones más altas podrían deberse a algún error sistemático desconocido en la medición de las estrellas variables cefeidas.

Medición de la constante de Hubble

Fecha de publicación	Constante de Hubble (km/s)/Mpc	Observador	Citación	Observaciones / metodología
19 de julio de 2023	67,0 ± 3,6	Sneppen y otros.	[97] [95]	Debido a los espectros de cuerpo negro de la contraparte óptica de las fusiones de estrellas de neutrones, estos sistemas proporcionan estimadores fuertemente restrictivos de la distancia cósmica.
13 de julio de 2023	68,3 ± 1,5	SPT-3G	[101]	Espectro de potencia CMB TT/TE/EE. Discrepancia inferior a 1 σ con respecto a Planck.
11-05-2023	66.6+4,1 -3,3	PL Kelly y otros.	[102]	Retardo temporal de las imágenes de supernovas captadas por lentes gravitacionales Refsdal . Independiente de la escala de distancias cósmicas o del CMB.
14 de diciembre de 2022	67.3+10,0 -9,1	S. Contarini y col.	[103]	Estadísticas de vacíos cósmicos utilizando el conjunto de datos BOSS DR12. [104]
08-02-2022	73.4+0,99 −1,22	Panteón+	[105]	Escalera de distancia SN Ia (+SH0ES)
17 de junio de 2022	75.4+3,8 -3,7	T. de Jaeger y col.	[106]	Utilice supernovas de tipo II como velas estandarizables para obtener una medición independiente de la constante de Hubble: 13 SNe II con distancias de la galaxia anfitriona medidas a partir de variables cefeidas, la punta de la rama gigante roja y la distancia geométrica (NGC 4258).
08-12-2021	73,04 ± 1,04	ZAPATOS	[107]	Cefeidas - Escalera de distancia SN Ia (HST+ Gaia EDR3 +"Pantheon+"). Discrepancia de 5 σ con Planck.
17 de septiembre de 2021	69,8 ± 1,7	W. Freedman	[108]	Indicador de distancia de la punta de la rama gigante roja (TRGB) (HST+Gaia EDR3)
16 de diciembre de 2020	72,1 ± 2,0	Telescopio espacial Hubble y Gaia EDR3	[109]	Combinando trabajos anteriores sobre estrellas gigantes rojas , utilizando el indicador de distancia de la punta de la rama gigante roja (TRGB), con mediciones de paralaje de Omega Centauri de Gaia EDR3.
15 de diciembre de 2020	73,2 ± 1,3	Telescopio espacial Hubble y Gaia EDR3	[110]	Combinación de la fotometría del HST y las paralajes de Gaia EDR3 para las cefeidas de la Vía Láctea , reduciendo la incertidumbre en la calibración de las luminosidades de las cefeidas al 1,0 %. La incertidumbre general en el valor de H 0 es del 1,8 %, que se espera que se reduzca al 1,3 % con una muestra más grande de supernovas de tipo Ia en galaxias que son anfitrionas conocidas de cefeidas. Continuación de una colaboración conocida como Supernovas, H 0 , para la ecuación de estado de la energía oscura (SHoES).
04-12-2020	73,5 ± 5,3	EJ Baxter, analista de negocios Sherwin	[111]	La lente gravitacional en el CMB se utiliza para estimar H 0 sin hacer referencia a la escala del horizonte sonoro , lo que proporciona un método alternativo para analizar los datos de Planck.
25 de noviembre de 2020	71.8+3,9 -3,3	P. Denzel y otros.	[112]	Se utilizan ocho sistemas de galaxias con lentes cuádruples para determinar H 0 con una precisión del 5%, de acuerdo con las estimaciones tanto del universo "temprano" como del "tardío". Independientemente de las escalas de distancia y del fondo cósmico de microondas.
7 de noviembre de 2020	67,4 ± 1,0	T. Sedgwick y otros.	[113]	Derivado de 88 0,02 < z < 0,05 Supernovas de tipo Ia utilizadas como indicadores de distancia de vela estándar. La estimación de H 0 se corrige para los efectos de las velocidades peculiares en los entornos de supernova, como se estima a partir del campo de densidad de galaxias. El resultado supone Ω m = 0,3 , Ω Λ = 0,7 y un horizonte sólido de149,3 Mpc , valor tomado de Anderson et al. (2014). [114]
29 de septiembre de 2020	67.6+4,3 -4,2	S. Mukherjee y otros.	[115]	Ondas gravitacionales , suponiendo que la ZTF19abanrh transitoria encontrada por el Zwicky Transient Facility es la contraparte óptica de GW190521 . Independiente de las escalas de distancia y del fondo cósmico de microondas.
18 de junio de 2020	75.8+5,2 -4,9	T. de Jaeger y col.	[116]	Utilice supernovas de tipo II como velas estandarizables para obtener una medición independiente de la constante de Hubble: 7 SNe II con distancias a la galaxia anfitriona medidas a partir de variables cefeidas o la punta de la rama gigante roja.
26 de febrero de 2020	73,9 ± 3,0	Proyecto de cosmología Megamaser	[93]	Mediciones de distancias geométricas a galaxias que albergan megamáseres. Independientes de las escalas de distancias y del fondo cósmico de microondas.
14 de octubre de 2019	74.2+2,7 −3,0	PASOS	[117]	Modelado de la distribución de masa y el retardo temporal del cuásar con lente DES J0408-5354.
12 de septiembre de 2019	76,8 ± 2,6	AFILADO/H0LiCOW	[118]	Modelado de tres objetos con lentes galácticas y sus lentes utilizando óptica adaptativa terrestre y el telescopio espacial Hubble.
20 de agosto de 2019	73.3+1,36 -1,35	K. Dutta y otros.	[119]	Esto se obtiene analizando datos cosmológicos de bajo corrimiento al rojo dentro del modelo ΛCDM. Los conjuntos de datos utilizados son supernovas de tipo Ia, oscilaciones acústicas bariónicas , mediciones de retardo temporal mediante lentes fuertes, mediciones de H ( z ) utilizando cronómetros cósmicos y mediciones de crecimiento a partir de observaciones de estructuras a gran escala.${\displaystyle H_{0}}$
15 de agosto de 2019	73,5 ± 1,4	MJ Reid, DW Pesce, Fiscal General Riess	[120]	Medición de la distancia a Messier 106 utilizando su agujero negro supermasivo, combinado con mediciones de sistemas binarios eclipsantes en la Gran Nube de Magallanes.
16 de julio de 2019	69,8 ± 1,9	Telescopio espacial Hubble	[90] [91] [92]	Las distancias a las estrellas gigantes rojas se calculan utilizando el indicador de distancia de la punta de la rama gigante roja (TRGB).
10 de julio de 2019	73.3+1,7 -1,8	Colaboración H0LiCOW	[121]	Observaciones actualizadas de cuásares con imágenes múltiples, ahora utilizando seis cuásares, independientemente de la escala de distancia cósmica e independiente de las mediciones del fondo cósmico de microondas.
08-07-2019	70.3+5,3 -5,0	La colaboración científica LIGO y la colaboración Virgo	[89]	Utiliza la contraparte de radio de GW170817, combinada con datos anteriores de ondas gravitacionales (GW) y electromagnéticas (EM).
28-03-2019	68.0+4,2 -4,1	Fermi-LAT	[122]	Atenuación de rayos gamma debida a luz extragaláctica. Independiente de la escala de distancias cósmicas y del fondo cósmico de microondas.
18-03-2019	74,03 ± 1,42	Telescopio espacial Hubble	[83]	La fotometría de precisión del HST de las cefeidas en la Gran Nube de Magallanes (LMC) reduce la incertidumbre en la distancia a la LMC del 2,5% al ​​1,3%. La revisión aumenta la tensión con las mediciones del CMB al nivel de 4,4 σ (P=99,999% para errores gaussianos), elevando la discrepancia más allá de un nivel plausible de probabilidad. Continuación de una colaboración conocida como Supernovae, H 0 , para la Ecuación de Estado de la Energía Oscura (SHoES).
08-02-2019	67,78+0,91 -0,87	Joseph Ryan y otros.	[123]	Tamaño angular de los cuásares y oscilaciones acústicas de bariones, suponiendo un modelo ΛCDM plano. Los modelos alternativos dan como resultado valores diferentes (generalmente más bajos) para la constante de Hubble.
6 de noviembre de 2018	67,77 ± 1,30	Encuesta sobre energía oscura	[124]	Mediciones de supernovas utilizando el método de escalera de distancia inversa basado en oscilaciones acústicas bariónicas.
5 de septiembre de 2018	72,5+2,1 -2,3	Colaboración H0LiCOW	[125]	Observaciones de cuásares con imágenes múltiples, independientemente de la escala de distancias cósmicas e independientes de las mediciones del fondo cósmico de microondas.
18 de julio de 2018	67,66 ± 0,42	Misión Planck	[126]	Resultados finales del Planck 2018.
27 de abril de 2018	73,52 ± 1,62	El telescopio espacial Hubble y Gaia	[127] [128]	Fotometría adicional del HST de las cefeidas galácticas con mediciones tempranas de paralaje de Gaia. El valor revisado aumenta la tensión con mediciones del CMB en el nivel 3,8 σ . Continuación de la colaboración SHoES.
22 de febrero de 2018	73,45 ± 1,66	Telescopio espacial Hubble	[129] [130]	Medidas de paralaje de las cefeidas galácticas para una mejor calibración de la escala de distancias ; el valor sugiere una discrepancia con las mediciones del CMB en el nivel 3,7 σ . Se espera que la incertidumbre se reduzca por debajo del 1% con la publicación final del catálogo de Gaia. Colaboración SHoES.
16 de octubre de 2017	70.0+12,0 −8,0	La colaboración científica LIGO y la colaboración Virgo	[131]	Medición de sirena estándar independiente de las técnicas normales de "vela estándar"; el análisis de ondas gravitacionales de una fusión de estrellas de neutrones binarias (BNS) GW170817 estimó directamente la distancia de luminosidad a escalas cosmológicas. Una estimación de cincuenta detecciones similares en la próxima década puede arbitrar la tensión de otras metodologías. [132] La detección y el análisis de una fusión de estrellas de neutrones y agujeros negros (NSBH) puede proporcionar una mayor precisión de la que podría permitir la BNS. [133]
22 de noviembre de 2016	71.9+2,4 −3,0	Telescopio espacial Hubble	[134]	Utiliza retrasos temporales entre múltiples imágenes de fuentes variables distantes producidas por un fuerte efecto de lente gravitacional . Colaboración conocida como Lentes H0 en Wellspring de COSMOGRAIL (H0LiCOW).
04-08-2016	76.2+3,4 -2,7	Flujos cósmicos-3	[135]	Comparación del corrimiento al rojo con otros métodos de distancia, incluidos los de Tully-Fisher , la variable cefeida y las supernovas de tipo Ia. Una estimación restrictiva a partir de los datos implica un valor más preciso de75 ± 2 .
13 de julio de 2016	67.6+0,7 -0,6	Estudio espectroscópico de oscilación bariónica (BOSS) del SDSS-III	[136]	Oscilaciones acústicas de bariones. En 2014 se inició un estudio ampliado (eBOSS) que se espera que se prolongue hasta 2020. El estudio ampliado está diseñado para explorar el momento en que el universo se estaba alejando de los efectos de desaceleración de la gravedad entre 3 y 8 mil millones de años después del Big Bang. [137]
17 de mayo de 2016	73,24 ± 1,74	Telescopio espacial Hubble	[138]	Supernova de tipo Ia : se espera que la incertidumbre se reduzca en un factor de más de dos con las próximas mediciones de Gaia y otras mejoras. Colaboración SHoES.
2015-02	67,74 ± 0,46	Misión Planck	[139] [140]	Los resultados de un análisis de la misión completa de Planck se hicieron públicos el 1 de diciembre de 2014 en una conferencia en Ferrara , Italia. En febrero de 2015 se publicó un conjunto completo de documentos que detallaban los resultados de la misión.
1 de octubre de 2013	74,4 ± 3,0	Flujos cósmicos-2	[141]	Comparación del corrimiento al rojo con otros métodos de distancia, incluidos Tully-Fisher, la variable Cefeida y las supernovas de tipo Ia.
21 de marzo de 2013	67,80 ± 0,77	Misión Planck	[57] [142] [143] [144] [145]	La sonda Planck Surveyor de la ESA se lanzó en mayo de 2009. Durante un período de cuatro años, realizó una investigación significativamente más detallada de la radiación cósmica de microondas que las investigaciones anteriores utilizando radiómetros HEMT y tecnología de bolómetro para medir el CMB a una escala menor que WMAP. El 21 de marzo de 2013, el equipo de investigación liderado por Europa detrás de la sonda cosmológica Planck publicó los datos de la misión, incluido un nuevo mapa del cielo completo del CMB y su determinación de la constante de Hubble.
20 de diciembre de 2012	69,32 ± 0,80	WMAP (9 años), combinado con otras mediciones	[146]
2010	70.4+1,3 -1,4	WMAP (7 años), combinado con otras mediciones	[147]	Estos valores surgen de ajustar una combinación de WMAP y otros datos cosmológicos a la versión más simple del modelo ΛCDM. Si los datos se ajustan con versiones más generales, H 0 tiende a ser menor y más incierta: típicamente alrededor de67 ± 4 (km/s)/Mpc aunque algunos modelos permiten valores cercanos63 (km/s)/Mpc . [148]
2010	71,0 ± 2,5	Sólo WMAP (7 años).	[147]
2009-02	70,5 ± 1,3	WMAP (5 años), combinado con otras mediciones	[149]
2009-02	71.9+2,6 -2,7	Sólo WMAP (5 años)	[149]
2007	70.4+1,5 -1,6	WMAP (3 años), combinado con otras mediciones	[150]
2006-08	76,9+10,7 -8,7	Observatorio de rayos X Chandra	[151]	Efecto Sunyaev–Zeldovich combinado y observaciones de rayos X de Chandra de cúmulos de galaxias . Incertidumbre ajustada en la tabla de la Colaboración Planck 2013. [152]
2003	72 ± 5	WMAP (primer año) únicamente	. [153]
2001-05	72 ± 8	Proyecto clave del telescopio espacial Hubble	[29]	Este proyecto estableció la determinación óptica más precisa, consistente con una medición de H 0 basada en observaciones del efecto Sunyaev–Zel'dovich de muchos cúmulos de galaxias que tienen una precisión similar.
antes de 1996	50 —90 (aprox.)		[63]
1994	67 ± 7	Formas de la curva de luz de la supernova 1a	[154]	Relación determinada entre la luminosidad de las SN 1a y las formas de sus curvas de luz. Riess et al. utilizaron esta relación entre la curva de luz de SN 1972E y la distancia de las cefeidas a NGC 5253 para determinar la constante.
mediados de los años 1970	100 ± 10	Gerard de Vaucouleurs	[64]	De Vaucouleurs creía que había mejorado la precisión de la constante de Hubble con respecto a la de Sandage porque utilizó cinco veces más indicadores primarios, diez veces más métodos de calibración, dos veces más indicadores secundarios y tres veces más puntos de datos de galaxias para derivar su100 ± 10 .
principios de los años 1970	55 (aprox.)	Allan Sandage y Gustav Tammann	[155]
1958	75 (aprox.)	Allan Sandage	[156]	Esta fue la primera buena estimación de H 0 , pero pasarían décadas antes de que se alcanzara un consenso.
1956	180	Humason , Mayall y Sandage	[155]
1929	500	Edwin Hubble , telescopio Hooker	[157] [155] [158]
1927	625	Georges Lemaître	[159]	Primera medición e interpretación como señal de la expansión del universo .

• Aceleración de la expansión del universo  – Fenómeno cosmológico
• Cosmología  : estudio científico del origen, la evolución y el destino final del universo.
• Materia oscura  : concepto en cosmología
• Lista de científicos cuyos nombres se utilizan en constantes físicas
• Pruebas de la relatividad general
• Tensión S8 : un problema similar de otro parámetro del modelo ΛCDM.