Escalera de distancia cósmica
La introducción de este artículo puede ser demasiado breve para resumir adecuadamente los puntos clave . ( Enero de 2023 ) |

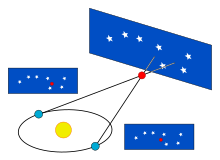
- Cajas de color verde claro: Técnica aplicable a galaxias formadoras de estrellas .
- Cajas de color azul claro: Técnica aplicable a galaxias de población II .
- Cajas de color violeta claro: Técnica de distancia geométrica.
- Recuadro rojo claro: La técnica de la función de luminosidad de la nebulosa planetaria es aplicable a todas las poblaciones del supercúmulo de Virgo .
- Líneas negras sólidas: Escalón de escalera bien calibrado.
- Líneas negras discontinuas: paso de escalera de calibración incierto.
La escala de distancias cósmicas (también conocida como escala de distancias extragalácticas ) es la sucesión de métodos mediante los cuales los astrónomos determinan las distancias a los objetos celestes. Una medición directa de la distancia de un objeto astronómico es posible solo para aquellos objetos que están "lo suficientemente cerca" (dentro de unos mil parsecs ) de la Tierra. Las técnicas para determinar distancias a objetos más distantes se basan en varias correlaciones medidas entre métodos que funcionan a distancias cercanas y métodos que funcionan a distancias mayores. Varios métodos se basan en una candela estándar, que es un objeto astronómico que tiene una luminosidad conocida .
La analogía de la escalera surge porque no existe una única técnica que pueda medir distancias en todos los rangos que se encuentran en astronomía. En cambio, se puede utilizar un método para medir distancias cercanas, un segundo método para medir distancias cercanas e intermedias, y así sucesivamente. Cada peldaño de la escalera proporciona información que se puede utilizar para determinar las distancias en el peldaño inmediatamente superior.
Medición directa

En la base de la escala se encuentran las mediciones de distancias fundamentales , en las que las distancias se determinan directamente, sin suposiciones físicas sobre la naturaleza del objeto en cuestión. La medición precisa de las posiciones estelares es parte de la disciplina de la astrometría . Las primeras distancias fundamentales, como los radios de la Tierra, la Luna y el Sol, y las distancias entre ellos, fueron estimadas correctamente por los antiguos griegos con tecnología muy básica. [2]
Unidad astronómica
Las mediciones directas de distancia se basan en la unidad astronómica (UA), que se define como la distancia media entre la Tierra y el Sol . Las leyes de Kepler proporcionan proporciones precisas de los tamaños de las órbitas de los objetos que orbitan alrededor del Sol, pero no proporcionan ninguna medida de la escala general del sistema orbital. El radar se utiliza para medir la distancia entre las órbitas de la Tierra y de un segundo cuerpo. A partir de esa medición y la relación de los dos tamaños de órbita, se calcula el tamaño de la órbita de la Tierra. La órbita de la Tierra se conoce con una precisión absoluta de unos pocos metros y una precisión relativa de unas pocas partes en 100 mil millones (1 × 10 −11 ).
Históricamente, las observaciones de los tránsitos de Venus fueron cruciales para determinar la UA; en la primera mitad del siglo XX, las observaciones de asteroides también fueron importantes. En la actualidad, la órbita de la Tierra se determina con alta precisión utilizando mediciones de radar de distancias a Venus y otros planetas y asteroides cercanos, [3] y rastreando naves espaciales interplanetarias en sus órbitas alrededor del Sol a través del Sistema Solar .
Paralaje

Las medidas de distancia fundamentales más importantes en astronomía provienen de la paralaje trigonométrico , tal como se aplica en el método de paralaje estelar . A medida que la Tierra orbita alrededor del Sol, la posición de las estrellas cercanas parecerá desplazarse ligeramente con respecto al fondo más distante. Estos desplazamientos son ángulos en un triángulo isósceles , con 2 UA (la distancia entre las posiciones extremas de la órbita de la Tierra alrededor del Sol) formando el cateto base del triángulo y la distancia a la estrella siendo los catetos largos de igual longitud. La cantidad de desplazamiento es bastante pequeña, incluso para las estrellas más cercanas, midiendo 1 segundo de arco para un objeto a una distancia de 1 pársec (3,26 años luz ), y luego disminuyendo en cantidad angular a medida que aumenta la distancia. Los astrónomos generalmente expresan las distancias en unidades de pársecs (segundos de arco de paralaje); los años luz se utilizan en los medios populares.
Debido a que la paralaje se hace más pequeña a mayor distancia estelar, las distancias útiles pueden medirse sólo para estrellas que están lo suficientemente cerca como para tener una paralaje mayor que unas pocas veces la precisión de la medición. En la década de 1990, por ejemplo, la misión Hipparcos obtuvo paralajes para más de cien mil estrellas con una precisión de alrededor de un milisegundo de arco , [4] proporcionando distancias útiles para estrellas de hasta unos pocos cientos de parsecs. La Wide Field Camera 3 del telescopio espacial Hubble tiene el potencial de proporcionar una precisión de 20 a 40 microsegundos de arco, lo que permite mediciones de distancias confiables de hasta 5000 parsecs (16 000 años luz) para pequeñas cantidades de estrellas. [5] [6] La misión espacial Gaia proporcionó distancias igualmente precisas para la mayoría de las estrellas más brillantes que la magnitud 15. [7]
Las distancias se pueden medir con un margen de error del 10% hasta el centro galáctico , a unos 30.000 años luz de distancia. Las estrellas tienen una velocidad relativa al Sol que provoca un movimiento propio (transversal a través del cielo) y una velocidad radial (movimiento hacia o desde el Sol). La primera se determina trazando la posición cambiante de las estrellas a lo largo de muchos años, mientras que la segunda proviene de la medición del desplazamiento Doppler del espectro de la estrella causado por el movimiento a lo largo de la línea de visión. Para un grupo de estrellas con la misma clase espectral y un rango de magnitud similar, se puede derivar una paralaje media a partir del análisis estadístico de los movimientos propios relativos a sus velocidades radiales. Este método de paralaje estadístico es útil para medir las distancias de estrellas brillantes más allá de los 50 parsecs y estrellas variables gigantes , incluidas las cefeidas y las variables RR Lyrae . [8]


El movimiento del Sol a través del espacio proporciona una línea de base más larga que aumentará la precisión de las mediciones de paralaje, conocida como paralaje secular . Para las estrellas en el disco de la Vía Láctea , esto corresponde a una línea de base media de 4 UA por año, mientras que para las estrellas del halo la línea de base es de 40 UA por año. Después de varias décadas, la línea de base puede ser órdenes de magnitud mayor que la línea de base Tierra-Sol utilizada para el paralaje tradicional. Sin embargo, el paralaje secular introduce un mayor nivel de incertidumbre porque la velocidad relativa de las estrellas observadas es una incógnita adicional. Cuando se aplica a muestras de múltiples estrellas, la incertidumbre se puede reducir; la incertidumbre es inversamente proporcional a la raíz cuadrada del tamaño de la muestra. [11]
La paralaje de cúmulos móviles es una técnica que permite utilizar los movimientos de estrellas individuales en un cúmulo estelar cercano para determinar la distancia al cúmulo. Solo los cúmulos abiertos están lo suficientemente cerca como para que esta técnica sea útil. En particular, la distancia obtenida para las Híades ha sido históricamente un paso importante en la escala de distancias.
En circunstancias especiales, se pueden realizar estimaciones de distancias fundamentales para otros objetos individuales. Si se puede observar la expansión de una nube de gas, como un remanente de supernova o una nebulosa planetaria , a lo largo del tiempo, se puede estimar una distancia de paralaje de expansión hasta esa nube. Sin embargo, esas mediciones sufren incertidumbres en la desviación del objeto de la esfericidad. Las estrellas binarias , que son binarias tanto visuales como espectroscópicas, también pueden tener su distancia estimada por medios similares y no sufren la incertidumbre geométrica mencionada anteriormente. La característica común de estos métodos es que se combina una medición del movimiento angular con una medición de la velocidad absoluta (generalmente obtenida a través del efecto Doppler ). La estimación de la distancia proviene del cálculo de qué tan lejos debe estar el objeto para que su velocidad absoluta observada aparezca con el movimiento angular observado.
En particular, las paralajes de expansión pueden proporcionar estimaciones fundamentales de la distancia para objetos que están muy lejos, porque los eyectados de supernova tienen grandes velocidades de expansión y tamaños grandes (en comparación con las estrellas). Además, se pueden observar con interferómetros de radio que pueden medir movimientos angulares muy pequeños. Estos se combinan para proporcionar estimaciones fundamentales de la distancia a las supernovas en otras galaxias. [12] Aunque valiosos, estos casos son bastante raros, por lo que sirven como comprobaciones de consistencia importantes en la escala de distancias en lugar de ser pasos de batalla por sí mismos.Velas estándar
Casi todos los objetos astronómicos utilizados como indicadores de distancia física pertenecen a una clase que tiene un brillo conocido. Al comparar esta luminosidad conocida con el brillo observado de un objeto, se puede calcular la distancia al objeto utilizando la ley del cuadrado inverso . Estos objetos de brillo conocido se denominan velas estándar , término acuñado por Henrietta Swan Leavitt . [13]
El brillo de un objeto se puede expresar en términos de su magnitud absoluta . Esta cantidad se deriva del logaritmo de su luminosidad vista desde una distancia de 10 parsecs. La magnitud aparente , la magnitud vista por el observador (se utiliza un instrumento llamado bolómetro ), se puede medir y utilizar con la magnitud absoluta para calcular la distancia d al objeto en parsecs [14] de la siguiente manera: o donde m es la magnitud aparente y M la magnitud absoluta. Para que esto sea preciso, ambas magnitudes deben estar en la misma banda de frecuencia y no puede haber movimiento relativo en la dirección radial. Se necesita algún medio para corregir la extinción interestelar, que también hace que los objetos parezcan más débiles y más rojos, especialmente si el objeto se encuentra dentro de una región polvorienta o gaseosa. [15] La diferencia entre las magnitudes absoluta y aparente de un objeto se llama módulo de distancia , y las distancias astronómicas, especialmente las intergalácticas, a veces se tabulan de esta manera.
Problemas
Existen dos problemas para cualquier clase de vela estándar. El principal es la calibración , es decir, la determinación de cuál es exactamente la magnitud absoluta de la vela. Esto incluye definir la clase lo suficientemente bien como para que se puedan reconocer los miembros y encontrar suficientes miembros de esa clase con distancias bien conocidas para permitir que se determine su verdadera magnitud absoluta con suficiente precisión. El segundo problema radica en reconocer los miembros de la clase y no utilizar por error una calibración de vela estándar en un objeto que no pertenece a la clase. A distancias extremas, que es donde más se desea utilizar un indicador de distancia, este problema de reconocimiento puede ser bastante grave.
Un problema importante con las velas estándar es la pregunta recurrente de cuán estándar son. Por ejemplo, todas las observaciones parecen indicar que las supernovas de Tipo Ia que están a una distancia conocida tienen el mismo brillo, corregido por la forma de la curva de luz. La base para esta proximidad en el brillo se analiza más adelante; sin embargo, existe la posibilidad de que las supernovas de Tipo Ia distantes tengan propiedades diferentes a las supernovas de Tipo Ia cercanas. El uso de supernovas de Tipo Ia es crucial para determinar el modelo cosmológico correcto . Si de hecho las propiedades de las supernovas de Tipo Ia son diferentes a grandes distancias, es decir, si la extrapolación de su calibración a distancias arbitrarias no es válida, ignorar esta variación puede sesgar peligrosamente la reconstrucción de los parámetros cosmológicos, en particular la reconstrucción del parámetro de densidad de materia . [16] [ aclaración necesaria ]
Que no se trata de una cuestión meramente filosófica se puede ver en la historia de las mediciones de distancias utilizando variables cefeidas . En la década de 1950, Walter Baade descubrió que las variables cefeidas cercanas utilizadas para calibrar la vela estándar eran de un tipo diferente a las utilizadas para medir distancias a galaxias cercanas. Las variables cefeidas cercanas eran estrellas de población I con un contenido de metales mucho mayor que las estrellas distantes de población II . Como resultado, las estrellas de población II eran en realidad mucho más brillantes de lo que se creía y, cuando se corrigió, esto tuvo el efecto de duplicar las estimaciones de distancias a los cúmulos globulares, las galaxias cercanas y el diámetro de la Vía Láctea. [ cita requerida ]
Recientemente se ha propuesto la kilonova como otro tipo de candela estándar. "Dado que las explosiones de kilonovas son esféricas, [17] los astrónomos podrían comparar el tamaño aparente de una explosión de supernova con su tamaño real tal como se ve a través del movimiento del gas, y así medir la tasa de expansión cósmica a diferentes distancias". [18]
Sirena estándar
Las ondas gravitacionales que se originan en la fase espiral de sistemas binarios compactos, como las estrellas de neutrones o los agujeros negros , tienen la propiedad útil de que la energía emitida como radiación gravitacional proviene exclusivamente de la energía orbital del par, y la contracción resultante de sus órbitas es directamente observable como un aumento en la frecuencia de las ondas gravitacionales emitidas. Para el orden principal , la tasa de cambio de frecuencia está dada por [19] [20] : 38 donde es la constante gravitacional , es la velocidad de la luz y es un número único (por lo tanto computable [a] ) llamado masa chirp del sistema, una combinación de las masas de los dos objetos [22] Al observar la forma de onda, se puede calcular la masa chirp y, a partir de ahí, la potencia (tasa de emisión de energía) de las ondas gravitacionales. Por lo tanto, dicha fuente de ondas gravitacionales es una sirena estándar de volumen conocido. [23] [20]
Al igual que con las velas estándar, dadas las amplitudes emitidas y recibidas, la ley del cuadrado inverso determina la distancia a la fuente. Sin embargo, existen algunas diferencias con las velas estándar. Las ondas gravitacionales no se emiten de forma isótropa, pero la medición de la polarización de la onda proporciona suficiente información para determinar el ángulo de emisión. Los detectores de ondas gravitacionales también tienen patrones de antena anisotrópicos, por lo que se necesita la posición de la fuente en el cielo en relación con los detectores para determinar el ángulo de recepción.
En general, si una red de tres detectores en diferentes ubicaciones detecta una onda, la red medirá suficiente información para realizar estas correcciones y obtener la distancia. Además, a diferencia de las velas estándar, las ondas gravitacionales no necesitan calibración con respecto a otras medidas de distancia. La medición de la distancia, por supuesto, requiere la calibración de los detectores de ondas gravitacionales, pero en ese caso la distancia se da fundamentalmente como un múltiplo de la longitud de onda de la luz láser que se utiliza en el interferómetro de ondas gravitacionales .
Existen otras consideraciones que limitan la precisión de esta distancia, además de la calibración del detector. Afortunadamente, las ondas gravitacionales no están sujetas a extinción debido a un medio absorbente intermedio. Pero están sujetas a lente gravitacional , de la misma manera que la luz. Si una señal está fuertemente lenteada , entonces podría ser recibida como múltiples eventos, separados en el tiempo, el análogo de múltiples imágenes de un cuásar, por ejemplo. Menos fácil de discernir y controlar es el efecto de lente débil , donde la trayectoria de la señal a través del espacio se ve afectada por muchos pequeños eventos de magnificación y demagnificación. Esto será importante para señales originadas en corrimientos al rojo cosmológicos mayores que 1. Es difícil para las redes de detectores medir la polarización de una señal con precisión si el sistema binario se observa casi de frente. [24] Tales señales sufren errores significativamente mayores en la medición de la distancia. Desafortunadamente, los binarios irradian más fuertemente perpendicularmente al plano orbital, por lo que las señales de frente son intrínsecamente más fuertes y las más comúnmente observadas.
Si el sistema binario está formado por un par de estrellas de neutrones, su fusión estará acompañada de una explosión de kilonova / hipernova que puede permitir que la posición sea identificada con precisión por telescopios electromagnéticos. En tales casos, el corrimiento al rojo de la galaxia anfitriona permite determinar la constante de Hubble . [22] Este fue el caso de GW170817 , que se utilizó para realizar la primera medición de este tipo. [25] Incluso si no se puede identificar una contraparte electromagnética para un conjunto de señales, es posible utilizar un método estadístico para inferir el valor de . [22]
Regla estándar
Otra clase de indicador de distancia física es la regla estándar . En 2008, se propusieron los diámetros de las galaxias como una posible regla estándar para la determinación de parámetros cosmológicos. [26] Más recientemente, se ha utilizado la escala física impresa por las oscilaciones acústicas bariónicas (BAO) en el universo temprano. En el universo temprano (antes de la recombinación ), los bariones y los fotones se dispersan entre sí y forman un fluido estrechamente acoplado que puede soportar ondas sonoras. Las ondas se originan por perturbaciones de densidad primordiales y viajan a una velocidad que se puede predecir a partir de la densidad bariónica y otros parámetros cosmológicos.
La distancia total que pueden viajar estas ondas sonoras antes de la recombinación determina una escala fija, que simplemente se expande con el universo después de la recombinación. Por lo tanto, la BAO proporciona una regla estándar que se puede medir en los estudios de galaxias a partir del efecto de los bariones en la agrupación de galaxias. El método requiere un estudio de galaxias extenso para hacer visible esta escala, pero se ha medido con precisión a nivel de porcentaje (ver oscilaciones acústicas de bariones ). La escala depende de parámetros cosmológicos como las densidades de bariones y materia, y el número de neutrinos, por lo que las distancias basadas en BAO dependen más del modelo cosmológico que las basadas en mediciones locales.
Los ecos de luz también se pueden utilizar como reglas estándar, [27] [28] aunque es un desafío medir correctamente la geometría de la fuente. [29] [30]
Indicadores de distancia galáctica
Con pocas excepciones, las distancias basadas en mediciones directas sólo están disponibles hasta unos mil parsecs, que es una porción modesta de nuestra propia galaxia. Para distancias superiores, las mediciones dependen de supuestos físicos, es decir, la afirmación de que se reconoce el objeto en cuestión y que la clase de objetos es lo suficientemente homogénea como para que sus miembros puedan utilizarse para una estimación significativa de la distancia.
Los indicadores de distancia física, utilizados en escalas de distancia progresivamente mayores, incluyen:
- Paralaje dinámico , utiliza parámetros orbitales de sistemas binarios visuales para medir la masa del sistema y, por lo tanto, utiliza la relación masa-luminosidad para determinar la luminosidad.
- Binarias eclipsantes : en la última década, se ha hecho posible la medición de los parámetros fundamentales de las binarias eclipsantes con telescopios de la clase de 8 metros. Esto hace posible su uso como indicadores de distancia. Recientemente, se han utilizado para proporcionar estimaciones directas de la distancia a la Gran Nube de Magallanes (LMC), la Pequeña Nube de Magallanes (SMC), la Galaxia de Andrómeda y la Galaxia del Triángulo . Las binarias eclipsantes ofrecen un método directo para medir la distancia a las galaxias con un nuevo nivel de precisión mejorado del 5%, lo que es factible con la tecnología actual hasta una distancia de alrededor de 3 Mpc (3 millones de parsecs). [31]
- Variables RR Lyrae : se utilizan para medir distancias dentro de la galaxia y en cúmulos globulares cercanos .
- Los cuatro indicadores siguientes utilizan estrellas de las poblaciones estelares antiguas (Población II): [32]
- Punta del indicador de distancia de la rama gigante roja (TRGB).
- Función de luminosidad de la nebulosa planetaria (PNLF)
- Función de luminosidad de los cúmulos globulares (GCLF)
- Fluctuación del brillo superficial (SBF)
- En astronomía galáctica, los estallidos de rayos X (destellos termonucleares en la superficie de una estrella de neutrones ) se utilizan como velas estándar. Las observaciones de estallidos de rayos X a veces muestran espectros de rayos X que indican expansión del radio. Por lo tanto, el flujo de rayos X en el pico del estallido debería corresponder a la luminosidad de Eddington , que se puede calcular una vez que se conoce la masa de la estrella de neutrones (1,5 masas solares es una suposición utilizada comúnmente). Este método permite la determinación de la distancia de algunos sistemas binarios de rayos X de baja masa . Los sistemas binarios de rayos X de baja masa son muy débiles en el óptico, lo que hace que sus distancias sean extremadamente difíciles de determinar.
- Los máseres interestelares se pueden utilizar para derivar distancias a objetos galácticos y algunos extragalácticos que tienen emisión de máser.
- Cefeidas y novas
- La relación Tully-Fisher
- La relación Faber-Jackson
- Supernovas de tipo Ia que tienen una magnitud absoluta máxima muy bien determinada en función de la forma de su curva de luz y son útiles para determinar distancias extragalácticas de hasta unos pocos cientos de Mpc. [33] Una notable excepción es SN 2003fg , la "Supernova de Champán", una supernova de tipo Ia de naturaleza inusual.
- Desplazamientos al rojo y ley de Hubble
Ajuste de secuencia principal
Cuando se representa gráficamente la magnitud absoluta de un grupo de estrellas frente a la clasificación espectral de la estrella, en un diagrama de Hertzsprung-Russell , se encuentran patrones evolutivos relacionados con la masa, la edad y la composición de la estrella. En particular, durante su período de combustión de hidrógeno, las estrellas se encuentran a lo largo de una curva en el diagrama llamada secuencia principal . Al medir estas propiedades a partir del espectro de una estrella, se puede determinar la posición de una estrella de secuencia principal en el diagrama H–R y, por lo tanto, estimar la magnitud absoluta de la estrella. Una comparación de este valor con la magnitud aparente permite determinar la distancia aproximada, después de corregir la extinción interestelar de la luminosidad debido al gas y al polvo.
En un cúmulo de estrellas ligado gravitacionalmente como las Híades , las estrellas se formaron aproximadamente con la misma edad y se encuentran a la misma distancia. Esto permite un ajuste relativamente preciso de la secuencia principal, lo que permite determinar tanto la edad como la distancia.
Escala de distancia extragaláctica
| Método | Incertidumbre para una galaxia única (magnitud) | Distancia al cúmulo de Virgo ( Mpc ) | Alcance (Mpc) |
|---|---|---|---|
| Cefeidas clásicas | 0,16 | 15–25 | 29 |
| Novas | 0,4 | 21,1 ± 3,9 | 20 |
| Función de luminosidad de la nebulosa planetaria | 0.3 | 15,4 ± 1,1 | 50 |
| Función de luminosidad de los cúmulos globulares | 0,4 | 18,8 ± 3,8 | 50 |
| Fluctuaciones del brillo de la superficie | 0.3 | 15,9 ± 0,9 | 50 |
| Relación sigma-d | 0,5 | 16,8 ± 2,4 | > 100 |
| Supernovas de tipo Ia | 0,10 | 19,4 ± 5,0 | > 1000 |
La escala de distancia extragaláctica es una serie de técnicas que utilizan hoy los astrónomos para determinar la distancia de los cuerpos cosmológicos más allá de nuestra propia galaxia, que no se obtienen fácilmente con los métodos tradicionales. Algunos procedimientos utilizan propiedades de estos objetos, como estrellas , cúmulos globulares , nebulosas y galaxias en su conjunto. Otros métodos se basan más en las estadísticas y probabilidades de cosas como cúmulos de galaxias enteros .
Efecto Wilson-Bappu
Descubierto en 1956 por Olin Wilson y MK Vainu Bappu , el efecto Wilson-Bappu utiliza el efecto conocido como paralaje espectroscópico . Muchas estrellas tienen características en sus espectros , como la línea K de calcio , que indican su magnitud absoluta . La distancia a la estrella puede calcularse a partir de su magnitud aparente utilizando el módulo de distancia .
Este método tiene importantes limitaciones para hallar distancias estelares. La calibración de las intensidades de las líneas espectrales tiene una precisión limitada y requiere una corrección por extinción interestelar . Aunque en teoría este método tiene la capacidad de proporcionar cálculos de distancias fiables a estrellas de hasta 7 megaparsecs (Mpc), generalmente solo se utiliza para estrellas de cientos de kiloparsecs (kpc).
Cefeidas clásicas
Más allá del alcance del efecto Wilson-Bappu , el siguiente método se basa en la relación período-luminosidad de las estrellas variables cefeidas clásicas . La siguiente relación se puede utilizar para calcular la distancia a las cefeidas clásicas galácticas y extragalácticas:
[35] [36]
Varios problemas complican el uso de las cefeidas como velas estándar y son objeto de intensos debates, entre los que destacan: la naturaleza y linealidad de la relación período-luminosidad en varias bandas de paso y el impacto de la metalicidad tanto en el punto cero como en la pendiente de esas relaciones, y los efectos de la contaminación fotométrica (mezcla) y una ley de extinción cambiante (normalmente desconocida) en las distancias de las cefeidas. [37] [38] [39] [40] [41] [42] [43] [44] [45]
Estos problemas no resueltos han dado lugar a valores citados para la constante de Hubble que oscilan entre 60 km/s/Mpc y 80 km/s/Mpc. Resolver esta discrepancia es uno de los principales problemas de la astronomía, ya que algunos parámetros cosmológicos del Universo pueden limitarse significativamente mejor proporcionando un valor preciso de la constante de Hubble. [46] [47]
Las estrellas variables cefeidas fueron el instrumento clave para que Edwin Hubble llegara en 1923 a la conclusión de que M31 (Andrómeda) era una galaxia externa, en lugar de una nebulosa más pequeña dentro de la Vía Láctea. Pudo calcular la distancia de M31 a 285 kpc, siendo el valor actual de 770 kpc. [ cita requerida ]
Según los hallazgos realizados hasta el momento, NGC 3370, una galaxia espiral en la constelación de Leo, contiene las cefeidas más lejanas que se han encontrado hasta ahora, a una distancia de 29 Mpc. Las estrellas variables cefeidas no son en absoluto marcadores de distancia perfectos: en las galaxias cercanas tienen un error de alrededor del 7% y de hasta el 15% en las más distantes. [48]
Supernovas

Existen varios métodos diferentes mediante los cuales se pueden utilizar las supernovas para medir distancias extragalácticas.
Medición de la fotosfera de una supernova
Podemos suponer que una supernova se expande de manera esféricamente simétrica. Si la supernova está lo suficientemente cerca como para que podamos medir la extensión angular, θ ( t ), de su fotosfera , podemos utilizar la ecuación
donde ω es la velocidad angular, θ es la extensión angular. Para obtener una medida precisa, es necesario realizar dos observaciones separadas por un tiempo Δ t . Posteriormente, podemos utilizar
donde d es la distancia a la supernova, V ej es la velocidad radial de la eyección de la supernova (se puede suponer que V ej es igual a V θ si es esféricamente simétrica).
Este método funciona únicamente si la supernova está lo suficientemente cerca como para poder medir con precisión la fotosfera. De manera similar, la capa de gas en expansión no es de hecho perfectamente esférica ni un cuerpo negro perfecto. Además, la extinción interestelar puede dificultar las mediciones precisas de la fotosfera. Este problema se ve agravado aún más por el colapso del núcleo de una supernova. Todos estos factores contribuyen al error de distancia de hasta el 25%.
Curvas de luz tipo Ia
Las supernovas de tipo Ia son una de las mejores formas de determinar distancias extragalácticas. Las Ia se producen cuando una estrella enana blanca binaria comienza a acumular materia de su estrella compañera. A medida que la enana blanca gana materia, finalmente alcanza su límite de Chandrasekhar de .
Una vez alcanzada, la estrella se vuelve inestable y sufre una reacción de fusión nuclear descontrolada. Debido a que todas las supernovas de tipo Ia explotan con aproximadamente la misma masa, sus magnitudes absolutas son todas iguales. Esto las hace muy útiles como velas estándar. Todas las supernovas de tipo Ia tienen una magnitud azul y visual estándar de
Por lo tanto, al observar una supernova de tipo Ia, si es posible determinar cuál fue su magnitud máxima, entonces se puede calcular su distancia. No es intrínsecamente necesario capturar la supernova directamente en su magnitud máxima; utilizando el método de la forma de la curva de luz multicolor ( MLCS ), la forma de la curva de luz (tomada en cualquier momento razonable después de la explosión inicial) se compara con una familia de curvas parametrizadas que determinarán la magnitud absoluta en el brillo máximo. Este método también tiene en cuenta la extinción/oscurecimiento interestelar causado por el polvo y el gas.
De manera similar, el método de estiramiento ajusta las curvas de luz de magnitud particular de supernovas a una curva de luz de plantilla. Esta plantilla, a diferencia de ser varias curvas de luz en diferentes longitudes de onda (MLCS), es solo una única curva de luz que se ha estirado (o comprimido) en el tiempo. Al usar este factor de estiramiento , se puede determinar la magnitud pico. [49]
El uso de supernovas de tipo Ia es uno de los métodos más precisos, sobre todo porque las explosiones de supernovas pueden ser visibles a grandes distancias (su luminosidad rivaliza con la de la galaxia en la que están situadas), mucho más lejos que las variables cefeidas (500 veces más lejos). Se ha dedicado mucho tiempo a perfeccionar este método. La incertidumbre actual se acerca a un mero 5%, lo que corresponde a una incertidumbre de sólo 0,1 magnitudes.
Novas en la determinación de la distancia
Las novas se pueden utilizar de forma muy similar a las supernovas para calcular distancias extragalácticas. Existe una relación directa entre la magnitud máxima de una nova y el tiempo que tarda su luz visible en disminuir en dos magnitudes. Se ha demostrado que esta relación es:
Donde es la derivada temporal de la magnitud de la nova, que describe la tasa promedio de disminución durante las primeras 2 magnitudes.
Una vez que las novas se desvanecen, son casi tan brillantes como las estrellas variables cefeidas más luminosas, por lo que ambas técnicas tienen aproximadamente la misma distancia máxima: ~ 20 Mpc. El error en este método produce una incertidumbre en la magnitud de aproximadamente ±0,4
Función de luminosidad de los cúmulos globulares
Basada en el método de comparación de las luminosidades de los cúmulos globulares (ubicados en halos galácticos) de galaxias distantes con la del cúmulo de Virgo , la función de luminosidad del cúmulo globular conlleva una incertidumbre de distancia de aproximadamente el 20% (o 0,4 magnitudes).
El astrónomo estadounidense William Alvin Baum fue el primero en utilizar cúmulos globulares para medir galaxias elípticas distantes. Comparó los cúmulos globulares más brillantes de la galaxia Virgo A con los de Andrómeda, suponiendo que la luminosidad de los cúmulos era la misma en ambos. Conociendo la distancia a Andrómeda, Baum supuso una correlación directa y estimó la distancia de Virgo A.
Baum utilizó un solo cúmulo globular, pero las formaciones individuales suelen ser velas estándar deficientes. El astrónomo canadiense René Racine supuso que el uso de la función de luminosidad de cúmulos globulares (GCLF) conduciría a una mejor aproximación. El número de cúmulos globulares en función de la magnitud viene dado por:
donde m 0 es la magnitud de rotación, M 0 es la magnitud del cúmulo de Virgo y sigma es la dispersión ~ 1,4 mag.
Se supone que todos los cúmulos globulares tienen aproximadamente la misma luminosidad dentro del universo . No existe una función de luminosidad universal para los cúmulos globulares que se aplique a todas las galaxias.
Función de luminosidad de la nebulosa planetaria
Al igual que el método GCLF, se puede utilizar un análisis numérico similar para las nebulosas planetarias en galaxias lejanas. La función de luminosidad de las nebulosas planetarias (PNLF) fue propuesta por primera vez a fines de la década de 1970 por Holland Cole y David Jenner. Sugirieron que todas las nebulosas planetarias podrían tener un brillo intrínseco máximo similar, que ahora se calcula en M = −4,53. Esto las convertiría, por lo tanto, en candelas estándar potenciales para determinar distancias extragalácticas.
El astrónomo George Howard Jacoby y sus colegas propusieron posteriormente que la función PNLF era igual a:
Donde N(M) es el número de nebulosas planetarias, con magnitud absoluta M. M* es igual a la nebulosa con la magnitud más brillante.
Método de fluctuación del brillo superficial

El siguiente método se ocupa de las propiedades inherentes generales de las galaxias. Estos métodos, aunque con porcentajes de error variables, tienen la capacidad de realizar estimaciones de distancias superiores a 100 Mpc, aunque normalmente se aplican de forma más local.
El método de fluctuación del brillo superficial (SBF) aprovecha el uso de cámaras CCD en telescopios. Debido a las fluctuaciones espaciales en el brillo superficial de una galaxia, algunos píxeles de estas cámaras captarán más estrellas que otros. A medida que aumenta la distancia, la imagen se volverá cada vez más suave. El análisis de esto describe una magnitud de la variación de píxel a píxel, que está directamente relacionada con la distancia de una galaxia. [50]
Relación sigma-d
La relación Sigma-D (o relación Σ-D), utilizada en galaxias elípticas , relaciona el diámetro angular (D) de la galaxia con su dispersión de velocidad . Es importante describir exactamente qué representa D para entender este método. Es, más precisamente, el diámetro angular de la galaxia hasta el nivel de brillo superficial de 20,75 B-mag arcsec −2 . Este brillo superficial es independiente de la distancia real de la galaxia a nosotros. En cambio, D es inversamente proporcional a la distancia de la galaxia, representada como d. Por lo tanto, esta relación no utiliza velas estándar. En cambio, D proporciona una regla estándar. Esta relación entre D y Σ es
donde C es una constante que depende de la distancia a los cúmulos de galaxias. [51]
Este método tiene el potencial de convertirse en uno de los métodos más potentes para calcular distancias galácticas, tal vez incluso superando el alcance del método de Tully-Fisher. Sin embargo, a día de hoy, las galaxias elípticas no son lo suficientemente brillantes como para permitir una calibración de este método mediante el uso de técnicas como las cefeidas. En su lugar, la calibración se realiza utilizando métodos más rudimentarios.
Superposición y escalado
Para determinar las distancias a otras galaxias se necesita una sucesión de indicadores de distancia, que es la escala de distancias. La razón es que los objetos lo suficientemente brillantes como para ser reconocidos y medidos a tales distancias son tan raros que hay pocos o ninguno presente cerca, por lo que hay muy pocos ejemplos lo suficientemente cercanos con paralaje trigonométrico confiable para calibrar el indicador. Por ejemplo, las variables cefeidas, uno de los mejores indicadores para las galaxias espirales cercanas , aún no se pueden calibrar satisfactoriamente solo por el paralaje, aunque la misión espacial Gaia ahora puede opinar sobre ese problema específico. La situación se complica aún más por el hecho de que las diferentes poblaciones estelares generalmente no tienen todos los tipos de estrellas en ellas.
Las cefeidas, en particular, son estrellas masivas, con vidas cortas, por lo que solo se las encontrará en lugares donde las estrellas se han formado muy recientemente. En consecuencia, como las galaxias elípticas por lo general han dejado de tener formación estelar a gran escala hace mucho tiempo, no tendrán cefeidas. En su lugar, se deben utilizar indicadores de distancia cuyo origen se encuentra en una población estelar más antigua (como las novas y las variables RR Lyrae). Las variables RR Lyrae son menos luminosas que las cefeidas, y las novas son impredecibles y se necesita un programa de monitoreo intensivo (y suerte durante ese programa) para reunir suficientes novas en la galaxia objetivo para una buena estimación de la distancia.
Como los escalones más distantes de la escala de distancias cósmicas dependen de los más cercanos, los escalones más distantes incluyen los efectos de los errores en los escalones más cercanos, tanto sistemáticos como estadísticos. El resultado de estos errores que se propagan significa que las distancias en astronomía rara vez se conocen con el mismo nivel de precisión que las mediciones en otras ciencias, y que la precisión es necesariamente menor para los tipos de objetos más distantes.
Otra preocupación, especialmente en el caso de las candelas estándar más brillantes, es su "estandarización": cuán homogéneos son los objetos en su verdadera magnitud absoluta. Para algunas de estas candelas estándar diferentes, la homogeneidad se basa en teorías sobre la formación y evolución de estrellas y galaxias, y por lo tanto también está sujeta a incertidumbres en esos aspectos. En el caso de los indicadores de distancia más luminosos, las supernovas de tipo Ia, se sabe que esta homogeneidad es deficiente. [52] [ aclaración necesaria ] Sin embargo, ninguna otra clase de objeto es lo suficientemente brillante como para ser detectado a distancias tan grandes, por lo que la clase es útil simplemente porque no hay una alternativa real.
El resultado observacional de la ley de Hubble, la relación proporcional entre la distancia y la velocidad con la que una galaxia se aleja de nosotros, generalmente denominada corrimiento al rojo, es un producto de la escala de distancias cósmicas. Edwin Hubble observó que las galaxias más débiles están más desplazadas al rojo. Encontrar el valor de la constante de Hubble fue el resultado de décadas de trabajo por parte de muchos astrónomos, tanto en la recopilación de mediciones de corrimientos al rojo de galaxias como en la calibración de los escalones de la escala de distancias. La ley de Hubble es el principal medio que tenemos para estimar las distancias de los cuásares y las galaxias distantes en las que no se pueden ver indicadores de distancia individuales.
Véase también
Notas al pie
- ^ Si la señal dependiera de las masas individuales por separado, no habría suficiente información observable en la señal en el orden más bajo para inferir su volumen intrínseco. Esta degeneración entre las masas es, por lo tanto, crucial para la medición del volumen, pero no es casualidad: tiene un origen fundamental en la naturaleza libre de escala de la gravedad en la relatividad general de Einstein. [21]
Referencias
- ^ "El Astrónomo". 16 de abril de 2013. Archivado desde el original el 9 de mayo de 2021. Consultado el 9 de mayo de 2021 .
- ^ Terence Tao. "Escalera de distancia cósmica" (PDF) . Consultado el 13 de mayo de 2023 .
- ^ Ash, ME; Shapiro, II; Smith, WB (1967). "Constantes astronómicas y efemérides planetarias deducidas a partir de observaciones ópticas y de radar". The Astronomical Journal . 72 : 338. Bibcode :1967AJ.....72..338A. doi : 10.1086/110230 .
- ^ Perryman, MAC; et al. (1999). "El catálogo HIPPARCOS". Astronomía y astrofísica . 323 : L49–L52. Código Bibliográfico :1997A&A...323L..49P.
- ^ Harrington, JD; Villard, R. (10 de abril de 2014). «El Hubble de la NASA extiende la cinta métrica estelar 10 veces más lejos en el espacio». NASA . Archivado desde el original el 17 de febrero de 2019 . Consultado el 17 de octubre de 2014 .
- ^ Riess, AG; Casertano, S.; Anderson, J.; MacKenty, J.; Filippenko, AV (2014). "Paralaje más allá de un kiloparsec a partir del escaneo espacial con la cámara de campo amplio 3 del telescopio espacial Hubble". The Astrophysical Journal . 785 (2): 161. arXiv : 1401.0484 . Código Bibliográfico :2014ApJ...785..161R. doi :10.1088/0004-637X/785/2/161. S2CID 55928992.
- ^ Brown, AGA ; et al. (Colaboración Gaia) (agosto de 2018). "Gaia Data Release 2: Resumen de los contenidos y propiedades del estudio". Astronomía y Astrofísica . 616 . A1. arXiv : 1804.09365 . Bibcode : 2018A&A...616A...1G . doi : 10.1051/0004-6361/201833051 .
- ^ B., Baidyanath (2003). Introducción a la astrofísica . PHI Learning Private Limited. ISBN 978-81-203-1121-3.
- ^ "Hubble descubre que el Universo podría estar expandiéndose más rápido de lo esperado". Archivado desde el original el 11 de septiembre de 2018 . Consultado el 3 de junio de 2016 .
- ^ "El Hubble estira la cinta métrica estelar diez veces más". Imágenes de la ESA/Hubble . Archivado desde el original el 30 de octubre de 2017. Consultado el 12 de abril de 2014 .
- ^ Popowski, P.; Gould, A. (1998). "Matemáticas de paralaje estadístico y escala de distancia local". arXiv : astro-ph/9703140 .
- ^ Bartel, N.; et al. (1994). "La forma, la tasa de expansión y la distancia de la supernova 1993J a partir de mediciones de VLBI". Nature . 368 (6472): 610–613. Bibcode :1994Natur.368..610B. doi :10.1038/368610a0. S2CID 4316734.
- ^ Fernie, JD (diciembre de 1969). "La relación entre período y luminosidad: una revisión histórica". Publicaciones de la Sociedad Astronómica del Pacífico . 81 (483): 707. Bibcode :1969PASP...81..707F. doi : 10.1086/128847 . ISSN 0004-6280.
- ^ "Cómo encontrar la distancia a las estrellas: módulo de distancia". Instalación Nacional del Telescopio de Australia. Archivado desde el original el 7 de noviembre de 2020. Consultado el 2 de noviembre de 2020 .
- ^ "Supernova de tipo Ia". Tema semanal . Caglow. Archivado desde el original el 29 de febrero de 2012 . Consultado el 30 de enero de 2012 .
- ^ Linden, S.; Virey, J.-M.; Tilquin, A. (2009). "Extracción de parámetros cosmológicos y sesgos de la evolución de la magnitud de las supernovas de tipo Ia". Astronomía y Astrofísica . 506 (3): 1095–1105. arXiv : 0907.4495 . Código Bibliográfico :2009A&A...506.1095L. doi :10.1051/0004-6361/200912811. S2CID 15178494.(Y referencias allí contenidas.)
- ^ Sneppen, Alberto; Watson, Darach; Bauswein, Andreas; Justo, Oliver; Kotak, Rubina; Nakar, Aod; Poznanski, Dovi; Sim, Stuart (febrero de 2023). "Simetría esférica en la kilonova AT2017gfo/GW170817". Naturaleza . 614 (7948): 436–439. arXiv : 2302.06621 . Código Bib :2023Natur.614..436S. doi :10.1038/s41586-022-05616-x. ISSN 1476-4687. PMID 36792736. S2CID 256846834.
- ^ "Cuando dos estrellas de neutrones colisionan, la explosión es perfectamente esférica". 17 de febrero de 2023.
- ^ Cutler, Curt; Flanagan, Éanna E. (15 de marzo de 1994). "Ondas gravitacionales de sistemas binarios compactos fusionados: ¿Con qué precisión se pueden extraer los parámetros del sistema binario de la forma de onda espiral?". Physical Review D . 49 (6): 2658–2697. arXiv : gr-qc/9402014 . Bibcode :1994PhRvD..49.2658C. doi :10.1103/PhysRevD.49.2658. PMID 10017261. S2CID 5808548.
- ^ ab Holz, Daniel E.; Hughes, Scott A.; Schutz, Bernard F. (diciembre de 2018). "Medición de distancias cósmicas con sirenas estándar". Physics Today . 71 (12): 34–40. Bibcode :2018PhT....71l..34H. doi : 10.1063/PT.3.4090 . ISSN 0031-9228.
- ^ Forward, Robert L. ; Berman, David (12 de junio de 1967). "Rango de detección de radiación gravitacional para sistemas estelares binarios". Physical Review Letters . 18 (24): 1071–1074. Bibcode :1967PhRvL..18.1071F. doi :10.1103/PhysRevLett.18.1071. ISSN 0031-9007.
- ^ abc Schutz, Bernard F. (25 de septiembre de 1986). "Determinación de la constante de Hubble a partir de observaciones de ondas gravitacionales". Nature . 323 (6086): 310–311. arXiv : 1307.2638 . Bibcode :1986Natur.323..310S. doi :10.1038/323310a0. hdl :11858/00-001M-0000-0013-73C1-2. ISSN 0028-0836. S2CID 4327285.
- ^ Hendry, Martin; Woan, Graham (febrero de 2007). "Astrofísica gravitacional" (PDF) . Astronomía y geofísica . 48 (1): 1.10–1.17. Bibcode :2007A&G....48a..10H. CiteSeerX 10.1.1.163.5500 . doi :10.1111/j.1468-4004.2007.48110.x. S2CID 8926158. Archivado (PDF) desde el original el 22 de diciembre de 2012 . Consultado el 4 de agosto de 2019 .
- ^ Nissanke, Samaya; Holz, Daniel E.; Hughes, Scott A.; Dalal, Neal; Sievers, Jonathan L. (10 de diciembre de 2010). "Explorando breves estallidos de rayos gamma como sirenas estándar de ondas gravitacionales". The Astrophysical Journal . 725 (1): 496–514. arXiv : 0904.1017 . Bibcode :2010ApJ...725..496N. doi :10.1088/0004-637X/725/1/496. hdl :1721.1/60956. ISSN 0004-637X. S2CID 14028891.
- ^ Abbott, BP; et al. ( Colaboración científica LIGO y Colaboración Virgo ) (16 de octubre de 2017). "Una medición de sirena estándar de ondas gravitacionales de la constante de Hubble". Nature . 551 (7678): 85–88. arXiv : 1710.05835 . Bibcode :2017Natur.551...85A. doi : 10.1038/nature24471 . PMID 29094696.
- ^ Marinoni, C.; et al. (2008). "Pruebas geométricas de modelos cosmológicos. I. Sondeo de la energía oscura utilizando la cinemática de galaxias de alto corrimiento al rojo". Astronomía y Astrofísica . 478 (1): 43–55. arXiv : 0710.0759 . Bibcode :2008A&A...478...43M. doi : 10.1051/0004-6361:20077116 . Archivado desde el original el 26 de enero de 2022 . Consultado el 23 de octubre de 2019 .
- ^ "Los ecos de luz susurran la distancia a una estrella" (Nota de prensa). Observatorio Europeo Austral . 11 de febrero de 2008. Archivado desde el original el 24 de septiembre de 2015. Consultado el 18 de octubre de 2015 .
- ^ Kervella, Pierre; Mérand, Antoine; Szabados, László; Fouqué, Pascal; Bersier, David; Pompei, Emanuela; Perrin, Guy (2 de marzo de 2008). "La cefeida galáctica de largo período RS Puppis I. Una distancia geométrica a partir de sus ecos de luz". Astronomía y astrofísica . 480 (1): 167–178. arXiv : 0802.1501 . Bibcode :2008A&A...480..167K. doi : 10.1051/0004-6361:20078961 .
derivamos una distancia geométrica de
1992 ± 28 pc a cachorro RS
- ^ Bond, Howard E.; Sparks, William B. (4 de marzo de 2009). "Sobre la determinación de la distancia geométrica a la cefeida RS Puppis a partir de sus ecos de luz". Astronomía y astrofísica . 495 (2): 371–377. arXiv : 0811.2943 . Bibcode :2009A&A...495..371B. doi : 10.1051/0004-6361:200810280 .
Concluimos que es probable que la mayoría de los nudos se encuentren, de hecho, frente al plano del cielo, lo que invalida el resultado de Kervella et al. [...] Aunque el resultado de la distancia de Kervella et al. queda invalidado, demostramos que las imágenes polarimétricas de alta resolución tienen el potencial de proporcionar una distancia geométrica válida a esta importante cefeida.
- ^ Kervella, Pierre; Bond, Howard E.; Cracraft, Misty; Szabados, László; Breitfelder, Joanne; Mérand2, Antoine; Sparks, William B.; Gallenne, Alexandre; Bersier, David; Fouqué, Pascal; Anderson, Richard I. (diciembre de 2014). "La cefeida galáctica de largo período RS Puppis. III. Una distancia geométrica a partir de imágenes polarimétricas del HST de sus ecos de luz". Astronomía y Astrofísica . 572 : A7 (13 págs.). arXiv : 1408.1697 . Bibcode :2014A&A...572A...7K. doi : 10.1051/0004-6361/201424395 .
Obtenemos una distancia de
1910 ± 80% (4,2%)
{{cite journal}}: CS1 maint: numeric names: authors list (link) - ^ Bonanos, AZ (2006). "Binarias eclipsantes: herramientas para calibrar la escala de distancias extragalácticas". Actas del Simposio de la IAU . 240 : 79–87. arXiv : astro-ph/0610923 . Código Bibliográfico :2007IAUS..240...79B. CiteSeerX 10.1.1.254.2692 . doi :10.1017/S1743921307003845. S2CID 18827791.
- ^ Ferrarese, L; et al. (2000). "Una base de datos de módulos de distancia de cefeidas y punta de la rama de gigantes rojas, función de luminosidad de cúmulos globulares, función de luminosidad de nebulosas planetarias y datos de fluctuación del brillo superficial útiles para determinaciones de distancia". The Astrophysical Journal Supplement Series . 128 (2): 431–459. arXiv : astro-ph/9910501 . Código Bibliográfico :2000ApJS..128..431F. doi :10.1086/313391. S2CID 121612286.
- ^ Colgate, SA (1979). "Supernovas como candela estándar para la cosmología". Astrophysical Journal . 232 (1): 404–408. Bibcode :1979ApJ...232..404C. doi :10.1086/157300.
- ^ Adaptado de George H. Jacoby; David Branch; Robin Ciardullo; Roger L. Davies; William E. Harris; Michael J. Pierce; Christopher J. Pritchet; John L. Tonry; Douglas L. Welch (1992). "Una revisión crítica de técnicas seleccionadas para medir distancias extragalácticas". Publicaciones de la Sociedad Astronómica del Pacífico . 104 (678): 599–662. Bibcode :1992PASP..104..599J. doi : 10.1086/133035 . JSTOR 40679907.
- ^ Benedict, G. Fritz et al. "Paralajes del sensor de guía fina del telescopio espacial Hubble de estrellas variables cefeidas galácticas: relaciones entre período y luminosidad" Archivado el 23 de enero de 2016 en Wayback Machine , The Astronomical Journal , volumen 133, número 4, págs. 1810–1827 (2007)
- ^ Majaess, Daniel; Turner, David; Moni Bidin, cristiana; Mauro, Francisco; Geisler, Douglas; Gieren, Wolfgang; Minniti, Dante; Chené, André-Nicolas; Lucas, Felipe; Borisova, Jura; Kurtev, Radostn; Dékány, Istvan; Saito, Roberto K. "Nueva evidencia que respalda la membresía de TW Nor en Lyngå 6 y el brazo espiral Centaurus" Archivado el 10 de marzo de 2017 en Wayback Machine , ApJ Letters , volumen 741, número 2, identificación del artículo. L2 (2011)
- ^ Stanek, KZ; Udalski, A. (1999). "El experimento de lente gravitacional óptica. Investigación de la influencia de la fusión en la escala de distancia de las cefeidas con cefeidas en la Gran Nube de Magallanes". arXiv : astro-ph/9909346 .
- ^ Udalski, A. ; Wyrzykowski, L.; Pietrzynski, G.; Szewczyk, O.; Szymanski, M.; Kubiak, M.; Soszynski, I.; Zebrun, K. (2001). "El experimento de lente gravitacional óptica. Cefeidas en la galaxia IC1613: no hay dependencia de la relación período-luminosidad en la metalicidad". Acta Astronomica . 51 : 221. arXiv : astro-ph/0109446 . Código Bibliográfico :2001AcA....51..221U.
- ^ Ngeow, C.; Kanbur, SM (2006). "La constante de Hubble de las supernovas de tipo Ia calibrada con las relaciones lineales y no lineales entre período y luminosidad de las cefeidas". The Astrophysical Journal . 642 (1): L29. arXiv : astro-ph/0603643 . Código Bibliográfico :2006ApJ...642L..29N. doi :10.1086/504478. S2CID 17860528.
- ^ Macri, LM; Stanek, KZ; Bersier, D.; Greenhill, LJ; Reid, MJ (2006). "Una nueva distancia de las cefeidas a la galaxia anfitriona del máser NGC 4258 y sus implicaciones para la constante de Hubble". The Astrophysical Journal . 652 (2): 1133–1149. arXiv : astro-ph/0608211 . Código Bibliográfico :2006ApJ...652.1133M. doi :10.1086/508530. S2CID 15728812.
- ^ Bono, G.; Caputo, F.; Fiorentino, G.; Marconi, M.; Musella, I. (2008). "Cefeidas en galaxias externas. I. La galaxia máser-anfitriona NGC 4258 y la dependencia de la metalicidad de las relaciones período-luminosidad y período-Wesenheit". The Astrophysical Journal . 684 (1): 102. arXiv : 0805.1592 . Código Bibliográfico :2008ApJ...684..102B. doi :10.1086/589965. S2CID 6275274.
- ^ Majaess, D.; Turner, D.; Carril, D. (2009). "Ceféidas tipo II como velas de distancia extragalácticas". Acta Astronómica . 59 (4): 403. arXiv : 0909.0181 . Código Bib : 2009AcA....59..403M.
- ^ Madore, Barry F.; Freedman, Wendy L. (2009). "Sobre la pendiente de la relación entre el período de las cefeidas y la luminosidad". The Astrophysical Journal . 696 (2): 1498–1501. arXiv : 0902.3747 . Código Bibliográfico :2009ApJ...696.1498M. doi :10.1088/0004-637X/696/2/1498. S2CID 16325249.
- ^ Scowcroft, V.; Bersier, D.; Mould, JR; Wood, PR (2009). "El efecto de la metalicidad en las magnitudes de las cefeidas y la distancia a M33". Monthly Notices of the Royal Astronomical Society . 396 (3): 43–47. arXiv : 0903.4088 . Bibcode :2009MNRAS.396.1287S. doi : 10.1111/j.1365-2966.2009.14822.x .
- ^ Majaess, D. (2010). "Las cefeidas de Centauro A (NGC 5128) e implicaciones para H0". Acta Astronómica . 60 (2): 121. arXiv : 1006.2458 . Código Bib : 2010AcA....60..121M.
- ^ Tammann, GA; Sandage, A.; Reindl, B. (2008). "El campo de expansión: El valor de H 0". Revista anual de astronomía y astrofísica . 15 (4): 289. arXiv : 0806.3018 . Código Bibliográfico :2008A&ARv..15..289T. doi :10.1007/s00159-008-0012-y. S2CID 18463474.
- ^ Freedman, Wendy L.; Madore, Barry F. (2010). "La constante de Hubble". Revista anual de astronomía y astrofísica . 48 : 673–710. arXiv : 1004.1856 . Código Bibliográfico :2010ARA&A..48..673F. doi :10.1146/annurev-astro-082708-101829. S2CID 119263173.
- ^ Welch, D. "Calibración e incertidumbres". Base de datos extragaláctica NASA/IPAC .
- ^ Coelho, R.; et al. (2015). "Estandarización de supernovas de tipo Ia". Revista Europea de Física . 36 (1): 015007. arXiv : 1411.3596 . Código Bibliográfico :2015EJPh...36a5007C. doi :10.1088/0143-0807/36/1/015007. S2CID 119096479.
- ^ Tonry, John L.; Dressler, Alan; Blakeslee, John P.; Ajhar, Edward A.; Fletcher, Andre B.; Luppino, Gerard A.; Metzger, Mark R.; Moore, Christopher B. (2001), "El estudio SBF de distancias galácticas. IV. Magnitudes, colores y distancias de SBF", Astrophysical Journal , 546 (2): 681–693, arXiv : astro-ph/0011223 , Bibcode :2001ApJ...546..681T, doi :10.1086/318301, S2CID 17628238
- ^ Dressler, Alan (1987). "La relación Dn-sigma para los bulbos de las galaxias de disco: una nueva medida independiente de la constante de Hubble". The Astrophysical Journal . 317 : 1. Bibcode :1987ApJ...317....1D. doi : 10.1086/165251 . ISSN 0004-637X.
- ^ Gilfanov, Marat; Bogdán, Ákos (2010). "Un límite superior en la contribución de las enanas blancas en proceso de acreción a la tasa de supernovas de tipo Ia". Nature . 463 (3): 924–925. arXiv : 1002.3359 . Bibcode :2010Natur.463..924G. doi :10.1038/nature08685. PMID 20164924. S2CID 4389201.
Bibliografía
- Carroll, Bradley W.; Ostlie, Dale A. (2014). Introducción a la astrofísica moderna . Harlow, Reino Unido: Pearson Education Limited . ISBN 978-1-292-02293-2.
- Medición del universo. La escalera de distancias cosmológicas , Stephen Webb, copyright 2001.
- Pasachoff, JM ; Filippenko, A. (2013). El cosmos: astronomía en el nuevo milenio (4.ª ed.). Cambridge: Cambridge University Press. ISBN 978-1-107-68756-1.
- The Astrophysical Journal , La función de luminosidad del cúmulo globular como indicador de distancia: efectos dinámicos , Ostriker y Gnedin, 5 de mayo de 1997.
- Introducción a la medición de distancias en astronomía , Richard de Grijs, Chichester: John Wiley & Sons, 2011, ISBN 978-0-470-51180-0 .
Enlaces externos
- El ABC de las distancias (UCLA)
- La escala de distancias extragalácticas de Bill Keel
- El telescopio espacial Hubble: un proyecto clave en la escala de distancias extragalácticas
- La constante de Hubble, una discusión histórica
- Escala de distancia cósmica de la NASA
- Base de datos de información del PNLF
- La revista astrofísica























