Tabla hash
| Tabla hash | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tipo | Matriz asociativa desordenada | |||||||||||||||||||||||
| Inventado | 1953 | |||||||||||||||||||||||
| ||||||||||||||||||||||||

En informática , una tabla hash es una estructura de datos que implementa una matriz asociativa , también llamada diccionario o simplemente mapa ; una matriz asociativa es un tipo de datos abstracto que asigna claves a valores . [2] Una tabla hash utiliza una función hash para calcular un índice , también llamado código hash , en una matriz de contenedores o ranuras , desde donde se puede encontrar el valor deseado. Durante la búsqueda, la clave se convierte en hash y el hash resultante indica dónde se almacena el valor correspondiente. Un mapa implementado por una tabla hash se llama mapa hash .
La mayoría de los diseños de tablas hash emplean una función hash imperfecta . Por lo tanto, las colisiones hash , en las que la función hash genera el mismo índice para más de una clave, normalmente deben solucionarse de alguna manera.
En una tabla hash bien dimensionada, la complejidad temporal promedio para cada búsqueda es independiente de la cantidad de elementos almacenados en la tabla. Muchos diseños de tablas hash también permiten inserciones y eliminaciones arbitrarias de pares clave-valor , a un costo promedio constante amortizado por operación. [3] [4] [5]
El hash es un ejemplo de un equilibrio entre el espacio y el tiempo . Si la memoria es infinita, se puede utilizar toda la clave directamente como índice para localizar su valor con un único acceso a la memoria. Por otro lado, si se dispone de tiempo infinito, se pueden almacenar valores sin tener en cuenta sus claves y se puede utilizar una búsqueda binaria o lineal para recuperar el elemento. [6] : 458
En muchas situaciones, las tablas hash resultan ser, en promedio, más eficientes que los árboles de búsqueda o cualquier otra estructura de búsqueda de tablas . Por este motivo, se utilizan ampliamente en muchos tipos de software informático , en particular para matrices asociativas , indexación de bases de datos , cachés y conjuntos .
Historia
La idea del hash surgió de forma independiente en diferentes lugares. En enero de 1953, Hans Peter Luhn escribió un memorando interno de IBM que utilizaba el hash con encadenamiento. El primer ejemplo de direccionamiento abierto fue propuesto por AD Linh, basándose en el memorando de Luhn. [4] : 547 Casi al mismo tiempo, Gene Amdahl , Elaine M. McGraw , Nathaniel Rochester y Arthur Samuel de IBM Research implementaron el hash para el ensamblador IBM 701. [7] : 124 El direccionamiento abierto con sondeo lineal se atribuye a Amdahl, aunque Andrey Ershov tuvo la misma idea de forma independiente. [7] : 124–125 El término "direccionamiento abierto" fue acuñado por W. Wesley Peterson en su artículo que analiza el problema de la búsqueda en archivos grandes. [8] : 15
El primer trabajo publicado sobre hash con encadenamiento se atribuye a Arnold Dumey , quien discutió la idea de usar el resto módulo un primo como función hash. [8] : 15 La palabra "hashing" fue publicada por primera vez en un artículo de Robert Morris. [7] : 126 Konheim y Weiss presentaron originalmente un análisis teórico del sondeo lineal. [8] : 15
Descripción general
Una matriz asociativa almacena un conjunto de pares (clave, valor) y permite la inserción, eliminación y búsqueda, con la restricción de claves únicas . En la implementación de la tabla hash de matrices asociativas, una matriz de longitud se llena parcialmente con elementos, donde . Un valor se almacena en una ubicación de índice , donde es una función hash y . [8] : 2 Bajo suposiciones razonables, las tablas hash tienen mejores límites de complejidad temporal en las operaciones de búsqueda, eliminación e inserción en comparación con los árboles de búsqueda binarios autoequilibrados . [8] : 1
Las tablas hash también se utilizan comúnmente para implementar conjuntos, omitiendo el valor almacenado para cada clave y simplemente rastreando si la clave está presente. [8] : 1
Factor de carga
Un factor de carga es una estadística crítica de una tabla hash y se define de la siguiente manera: [1] donde
- es el número de entradas ocupadas en la tabla hash.
- es el número de cubos.
El rendimiento de la tabla hash se deteriora en relación con el factor de carga . [8] : 2
El software normalmente garantiza que el factor de carga se mantenga por debajo de una cierta constante, . Esto ayuda a mantener un buen rendimiento. Por lo tanto, un enfoque común es cambiar el tamaño o "rehacer" la tabla hash cada vez que el factor de carga alcanza . De manera similar, la tabla también puede cambiar de tamaño si el factor de carga cae por debajo de . [9]
Factor de carga para encadenamiento separado
Con tablas hash de encadenamiento independientes, cada ranura de la matriz de contenedores almacena un puntero a una lista o matriz de datos. [10]
Las tablas hash de encadenamiento independientes sufren una disminución gradual del rendimiento a medida que aumenta el factor de carga, y no existe un punto fijo más allá del cual sea absolutamente necesario cambiar el tamaño. [9]
Con encadenamiento separado, el valor que ofrece el mejor rendimiento suele estar entre 1 y 3. [9]
Factor de carga para direccionamiento abierto
Con direccionamiento abierto, cada ranura de la matriz de contenedores contiene exactamente un elemento. Por lo tanto, una tabla hash con direccionamiento abierto no puede tener un factor de carga mayor que 1. [10]
El rendimiento del direccionamiento abierto se vuelve muy malo cuando el factor de carga se acerca a 1. [9]
Por lo tanto, una tabla hash que utiliza direccionamiento abierto debe redimensionarse o rehacerse si el factor de carga se acerca a 1. [9]
Con direccionamiento abierto, las cifras aceptables de factor de carga máxima deberían oscilar entre 0,6 y 0,75. [11] [12] : 110
Función hash
Una función hash asigna el universo de claves a índices o ranuras dentro de la tabla, es decir, para . Las implementaciones convencionales de funciones hash se basan en el supuesto del universo entero de que todos los elementos de la tabla provienen del universo , donde la longitud de bits de está confinada dentro del tamaño de palabra de una arquitectura de computadora . [8] : 2
Se dice que una función hash es perfecta para un conjunto dado si es inyectiva en , es decir, si cada elemento se asigna a un valor diferente en . [13] [14] Se puede crear una función hash perfecta si se conocen todas las claves de antemano. [13]
Supuesto del universo entero
Los esquemas de hash utilizados en el supuesto de universo entero incluyen hash por división, hash por multiplicación, hash universal , hash perfecto dinámico y hash perfecto estático . [8] : 2 Sin embargo, el hash por división es el esquema más utilizado. [15] : 264 [12] : 110
Hashing por división
El esquema en el hash por división es el siguiente: [8] : 2 donde es el valor hash de y es el tamaño de la tabla.
Hashing por multiplicación
El esquema en el hash por multiplicación es el siguiente: [8] : 2–3 Donde es una constante de valor real no entero y es el tamaño de la tabla. Una ventaja del hash por multiplicación es que no es crítico. [8] : 2–3 Aunque cualquier valor produce una función hash, Donald Knuth sugiere usar la proporción áurea . [8] : 3
Elección de una función hash
La distribución uniforme de los valores hash es un requisito fundamental de una función hash. Una distribución no uniforme aumenta la cantidad de colisiones y el costo de resolverlas. A veces es difícil garantizar la uniformidad por diseño, pero se puede evaluar empíricamente mediante pruebas estadísticas, por ejemplo, una prueba de chi-cuadrado de Pearson para distribuciones uniformes discretas. [16] [17]
La distribución debe ser uniforme solo para los tamaños de tabla que se dan en la aplicación. En particular, si se utiliza un redimensionamiento dinámico con duplicación exacta y reducción a la mitad del tamaño de la tabla, entonces la función hash debe ser uniforme solo cuando el tamaño sea una potencia de dos . En este caso, el índice se puede calcular como un rango de bits de la función hash. Por otro lado, algunos algoritmos hash prefieren que el tamaño sea un número primo . [18]
En el caso de los esquemas de direccionamiento abierto , la función hash también debería evitar la agrupación , es decir, la asignación de dos o más claves a ranuras consecutivas. Dicha agrupación puede hacer que el costo de búsqueda se dispare, incluso si el factor de carga es bajo y las colisiones son poco frecuentes. Se afirma que el popular hash multiplicativo tiene un comportamiento de agrupación particularmente deficiente. [18] [4]
El hash K-independiente ofrece una manera de probar que una determinada función hash no tiene conjuntos de claves incorrectos para un tipo dado de tabla hash. Se conocen varios resultados de K-independencia para esquemas de resolución de colisiones como el sondeo lineal y el hash cuckoo. Dado que la K-independencia puede probar que una función hash funciona, uno puede entonces enfocarse en encontrar la función hash más rápida posible. [19]
Resolución de colisiones
Un algoritmo de búsqueda que utiliza hash consta de dos partes. La primera parte consiste en calcular una función hash que transforma la clave de búsqueda en un índice de matriz . El caso ideal es aquel en el que no hay dos claves de búsqueda que tengan el mismo índice de matriz. Sin embargo, este no siempre es el caso y es imposible garantizarlo para datos no visibles. [20] : 515 Por lo tanto, la segunda parte del algoritmo es la resolución de colisiones. Los dos métodos comunes para la resolución de colisiones son el encadenamiento separado y el direccionamiento abierto. [6] : 458
Encadenamiento separado
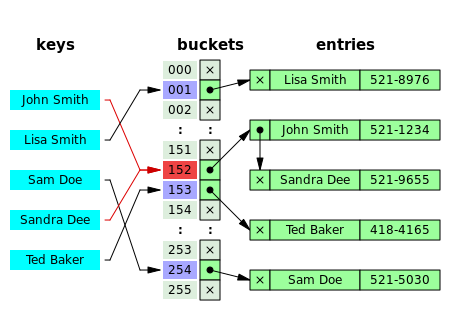

En el encadenamiento por separado, el proceso implica la construcción de una lista enlazada con un par clave-valor para cada índice de matriz de búsqueda. Los elementos colisionados se encadenan entre sí a través de una única lista enlazada, que se puede recorrer para acceder al elemento con una clave de búsqueda única. [6] : 464 La resolución de colisiones a través del encadenamiento con lista enlazada es un método común de implementación de tablas hash. Sea y la tabla hash y el nodo respectivamente, la operación implica lo siguiente: [15] : 258
Chained-Hash-Insert( T , k ) inserta x al principio de la lista enlazada T [ h ( k )]Chained-Hash-Search( T , k ) busca un elemento con clave k en una lista enlazada T [ h ( k )]Chained-Hash-Delete( T , k ) elimina x de la lista enlazada T [ h ( k )]
Si el elemento es comparable numérica o léxicamente y se inserta en la lista manteniendo el orden total , resulta en una terminación más rápida de las búsquedas fallidas. [20] : 520–521
Otras estructuras de datos para encadenamiento separado
Si las claves están ordenadas , podría ser eficiente utilizar conceptos " autoorganizados " como el uso de un árbol binario de búsqueda autoequilibrado , a través del cual se podría reducir el peor caso teórico a , aunque introduce complejidades adicionales. [20] : 521
En el hash dinámico perfecto , se utilizan tablas hash de dos niveles para reducir la complejidad de búsqueda y garantizar que sea una tarea en el peor de los casos. En esta técnica, los grupos de entradas se organizan como tablas hash perfectas con ranuras que proporcionan un tiempo de búsqueda constante en el peor de los casos y un tiempo amortizado bajo para la inserción. [21] Un estudio muestra que el encadenamiento separado basado en matrices tiene un 97 % más de rendimiento en comparación con el método de lista enlazada estándar bajo carga pesada. [22] : 99
Técnicas como el uso de árboles de fusión para cada grupo también dan como resultado un tiempo constante para todas las operaciones con alta probabilidad. [23]
Almacenamiento en caché y localidad de referencia
La lista enlazada de la implementación de encadenamiento independiente puede no ser consciente de la memoria caché debido a la localidad espacial ( localidad de referencia ) cuando los nodos de la lista enlazada están dispersos en la memoria, por lo que el recorrido de la lista durante la inserción y la búsqueda puede implicar ineficiencias de la memoria caché de la CPU . [22] : 91
En las variantes de resolución de colisiones que tienen en cuenta la memoria caché mediante encadenamiento separado, se utiliza una matriz dinámica que es más compatible con la memoria caché en el lugar donde normalmente se implementa una lista enlazada o árboles de búsqueda binarios autoequilibrados, ya que el patrón de asignación contiguo de la matriz podría ser explotado por prefetchers de memoria caché de hardware (como el búfer de búsqueda de traducción) , lo que da como resultado un menor tiempo de acceso y consumo de memoria. [24] [25] [26]
Direccionamiento abierto


El direccionamiento abierto es otra técnica de resolución de colisiones en la que cada registro de entrada se almacena en la propia matriz de contenedores y la resolución de hash se realiza mediante sondeo . Cuando se debe insertar una nueva entrada, se examinan los contenedores, comenzando con la ranura a la que se le ha aplicado el hash y siguiendo una secuencia de sondeo , hasta que se encuentra una ranura desocupada. Cuando se busca una entrada, se escanean los contenedores en la misma secuencia, hasta que se encuentra el registro de destino o una ranura de matriz sin usar, lo que indica una búsqueda fallida. [27]
Las secuencias de sonda más conocidas incluyen:
- Sondeo lineal , en el que el intervalo entre sondas es fijo (normalmente 1). [28]
- Sondeo cuadrático , en el que el intervalo entre sondeos se incrementa añadiendo las salidas sucesivas de un polinomio cuadrático al valor dado por el cálculo hash original. [29] : 272
- Doble hash , en el que el intervalo entre sondas se calcula mediante una función hash secundaria. [29] : 272–273
El rendimiento del direccionamiento abierto puede ser más lento en comparación con el encadenamiento separado, ya que la secuencia de sondeo aumenta cuando el factor de carga se acerca a 1. [9] [22] : 93 El sondeo da como resultado un bucle infinito si el factor de carga llega a 1, en el caso de una tabla completamente llena. [6] : 471 El costo promedio del sondeo lineal depende de la capacidad de la función hash para distribuir los elementos de manera uniforme en toda la tabla para evitar la agrupación , ya que la formación de agrupaciones daría como resultado un mayor tiempo de búsqueda. [6] : 472
Almacenamiento en caché y localidad de referencia
Dado que las ranuras están ubicadas en posiciones sucesivas, el sondeo lineal podría conducir a una mejor utilización de la memoria caché de la CPU debido a la localidad de las referencias, lo que resulta en una latencia de memoria reducida . [28]
Otras técnicas de resolución de colisiones basadas en direccionamiento abierto
Hashing fusionado
El hash fusionado es un híbrido entre el encadenamiento independiente y el direccionamiento abierto en el que los contenedores o nodos se vinculan dentro de la tabla. [30] : 6–8 El algoritmo es ideal para la asignación de memoria fija . [30] : 4 La colisión en el hash fusionado se resuelve identificando la ranura vacía con el índice más grande en la tabla hash, luego el valor en colisión se inserta en esa ranura. El contenedor también está vinculado a la ranura del nodo insertado que contiene su dirección hash en colisión. [30] : 8
Hashing de cuco
El hash de cuco es una forma de técnica de resolución de colisiones de direccionamiento abierto que garantiza la complejidad de búsqueda en el peor de los casos y un tiempo amortizado constante para las inserciones. La colisión se resuelve mediante el mantenimiento de dos tablas hash, cada una con su propia función hash, y la ranura colisionada se reemplaza con el elemento dado, y el elemento ocupado de la ranura se desplaza a la otra tabla hash. El proceso continúa hasta que cada clave tiene su propio lugar en los contenedores vacíos de las tablas; si el procedimiento entra en un bucle infinito (lo que se identifica mediante el mantenimiento de un contador de bucle de umbral), ambas tablas hash se vuelven a codificar con funciones hash más nuevas y el procedimiento continúa. [31] : 124–125
Hashing de rayuela
El hash Hopscotch es un algoritmo basado en direccionamiento abierto que combina los elementos del hash cuckoo , el sondeo lineal y el encadenamiento a través de la noción de un vecindario de contenedores (los contenedores subsiguientes alrededor de cualquier contenedor ocupado dado, también llamado contenedor "virtual"). [32] : 351–352 El algoritmo está diseñado para ofrecer un mejor rendimiento cuando el factor de carga de la tabla hash crece más allá del 90%; también proporciona un alto rendimiento en configuraciones concurrentes , por lo que es muy adecuado para implementar una tabla hash concurrente redimensionable . [32] : 350 La característica de vecindario del hash Hopscotch garantiza una propiedad de que el costo de encontrar el elemento deseado de cualquier contenedor dado dentro del vecindario es muy cercano al costo de encontrarlo en el contenedor mismo; el algoritmo intenta ser un elemento en su vecindario, con un posible costo involucrado en desplazar otros elementos. [32] : 352
Cada contenedor dentro de la tabla hash incluye una "información de salto" adicional: una matriz de bits de H -bits para indicar la distancia relativa del elemento que se ha convertido originalmente en el contenedor virtual actual dentro de H -1 entradas. [32] : 352 Sea y la clave que se va a insertar y el contenedor en el que se convierte la clave respectivamente; hay varios casos involucrados en el procedimiento de inserción de modo que se compromete la propiedad de vecindad del algoritmo: [32] : 352–353 si está vacío, se inserta el elemento y el bit más a la izquierda del mapa de bits se establece en 1; si no está vacío, se utiliza un sondeo lineal para encontrar una ranura vacía en la tabla, el mapa de bits del contenedor se actualiza seguido de la inserción; si la ranura vacía no está dentro del rango de la vecindad, es decir , H -1, se realiza un intercambio posterior y una manipulación de la matriz de bits de información de salto de cada contenedor de acuerdo con sus propiedades invariantes de vecindad . [32] : 353
Hash de Robin Hood
El hashing Robin Hood es un algoritmo de resolución de colisiones basado en direccionamiento abierto; las colisiones se resuelven favoreciendo el desplazamiento del elemento que está más alejado (o la longitud de secuencia de sonda (PSL) más larga) de su "ubicación de origen", es decir, el depósito en el que se ha introducido el elemento. [33] : 12 Aunque el hashing Robin Hood no cambia el coste teórico de búsqueda , afecta significativamente la varianza de la distribución de los elementos en los depósitos, [34] : 2 es decir, se ocupa de la formación de clústeres en la tabla hash. [35] Cada nodo dentro de la tabla hash que utiliza el hashing Robin Hood debe aumentarse para almacenar un valor PSL adicional. [36] Sea la clave que se va a insertar, la longitud PSL (incremental) de , la tabla hash y el índice, el procedimiento de inserción es el siguiente: [33] : 12–13 [37] : 5
- Si : la iteración pasa al siguiente segmento sin intentar una sonda externa.
- Si : inserte el elemento en el depósito ; intercambie con —déjelo ser ; continúe la sonda desde el primer depósito para insertar ; repita el procedimiento hasta que se inserte cada elemento.
Cambio de tamaño dinámico
Las inserciones repetidas hacen que el número de entradas en una tabla hash crezca, lo que en consecuencia aumenta el factor de carga; para mantener el rendimiento amortizado de las operaciones de búsqueda e inserción, una tabla hash se redimensiona dinámicamente y los elementos de las tablas se vuelven a codificar en los contenedores de la nueva tabla hash, [9] ya que los elementos no se pueden copiar ya que variar los tamaños de tabla da como resultado diferentes valores hash debido a la operación de módulo . [38] Si una tabla hash se vuelve "demasiado vacía" después de eliminar algunos elementos, se puede realizar un cambio de tamaño para evitar el uso excesivo de memoria . [39]
Cambiar el tamaño moviendo todas las entradas
Generalmente, se asigna de forma privada una nueva tabla hash con un tamaño que duplica al de la tabla hash original y cada elemento de la tabla hash original se mueve a la tabla recién asignada calculando los valores hash de los elementos seguidos de la operación de inserción. La repetición del hash es simple, pero computacionalmente costosa. [40] : 478–479
Alternativas a la repetición total
Algunas implementaciones de tablas hash, en particular en sistemas en tiempo real , no pueden pagar el precio de agrandar la tabla hash de una sola vez, porque puede interrumpir operaciones críticas en el tiempo. Si no se puede evitar el cambio de tamaño dinámico, una solución es realizar el cambio de tamaño gradualmente para evitar un bache de almacenamiento (normalmente al 50 % del tamaño de la nueva tabla) durante el rehashing y para evitar la fragmentación de la memoria que desencadena la compactación del montón debido a la desasignación de grandes bloques de memoria causada por la antigua tabla hash. [41] : 2–3 En tal caso, la operación de rehashing se realiza de forma incremental mediante la extensión del bloque de memoria anterior asignado para la antigua tabla hash de modo que los contenedores de la tabla hash permanezcan inalterados. Un enfoque común para el rehashing amortizado implica mantener dos funciones hash y . El proceso de rehacer el hash de los elementos de un depósito de acuerdo con la nueva función hash se denomina limpieza , que se implementa a través del patrón de comando encapsulando las operaciones como , y a través de un contenedor de modo que cada elemento en el depósito se rehace y su procedimiento implica lo siguiente: [41] : 3
- Cubo limpio .
- Cubo limpio .
- El comando se ejecuta.
Hashing lineal
El hash lineal es una implementación de la tabla hash que permite crecimientos o reducciones dinámicas de la tabla, un segmento a la vez. [42]
Actuación
El rendimiento de una tabla hash depende de la capacidad de la función hash para generar números cuasialeatorios ( ) para las entradas en la tabla hash donde , y denota la clave, el número de contenedores y la función hash tal que . Si la función hash genera lo mismo para claves distintas ( ), esto da como resultado una colisión , que se maneja de varias maneras. La complejidad de tiempo constante ( ) de la operación en una tabla hash se presupone con la condición de que la función hash no genere índices en colisión; por lo tanto, el rendimiento de la tabla hash es directamente proporcional a la capacidad de la función hash elegida para dispersar los índices. [43] : 1 Sin embargo, la construcción de una función hash de este tipo es prácticamente inviable , por lo que las implementaciones dependen de técnicas de resolución de colisiones específicas del caso para lograr un mayor rendimiento. [43] : 2
Aplicaciones
Matrices asociativas
Las tablas hash se utilizan comúnmente para implementar muchos tipos de tablas en memoria. Se utilizan para implementar matrices asociativas . [29]
Indexación de bases de datos
Las tablas hash también se pueden utilizar como estructuras de datos basadas en disco e índices de bases de datos (como en dbm ), aunque los árboles B son más populares en estas aplicaciones. [44]
Cachés
Las tablas hash se pueden utilizar para implementar cachés , tablas de datos auxiliares que se utilizan para acelerar el acceso a los datos que se almacenan principalmente en medios más lentos. En esta aplicación, las colisiones de hash se pueden manejar descartando una de las dos entradas en colisión, generalmente borrando el elemento antiguo que está almacenado actualmente en la tabla y sobrescribiéndolo con el nuevo elemento, de modo que cada elemento de la tabla tenga un valor hash único. [45] [46]
Conjuntos
Las tablas hash se pueden utilizar en la implementación de estructuras de datos de conjunto , que pueden almacenar valores únicos sin ningún orden particular; el conjunto se utiliza normalmente para probar la pertenencia de un valor en la colección, en lugar de la recuperación de elementos. [47]
Tabla de transposición
Una tabla de transposición a una tabla hash compleja que almacena información sobre cada sección que se ha buscado. [48]
Implementaciones
Muchos lenguajes de programación proporcionan la funcionalidad de tabla hash, ya sea como matrices asociativas integradas o como módulos de biblioteca estándar .
En JavaScript , un "objeto" es una colección mutable de pares clave-valor (llamados "propiedades"), donde cada clave es una cadena o un "símbolo" único garantizado; cualquier otro valor, cuando se utiliza como clave, primero se convierte en una cadena. Aparte de los siete tipos de datos "primitivos", cada valor en JavaScript es un objeto. [49] ECMAScript 2015 también agregó la Mapestructura de datos, que acepta valores arbitrarios como claves. [50]
C++11 incluye unordered_mapen su biblioteca estándar para almacenar claves y valores de tipos arbitrarios . [51]
Los implementos integrados de Gomap crean una tabla hash en forma de tipo . [52]
El lenguaje de programación Java incluye las colecciones HashSet, HashMap, LinkedHashSety LinkedHashMap genéricas . [53]
Los implementos integrados de Pythondict crean una tabla hash en forma de tipo . [54]
El modelo integrado de RubyHash utiliza el modelo de direccionamiento abierto desde Ruby 2.4 en adelante. [55]
El lenguaje de programación Rust incluye HashMap, HashSetcomo parte de la biblioteca estándar de Rust. [56]
La biblioteca estándar .NETHashSet incluye y Dictionary, [57] [58] por lo que se puede utilizar desde lenguajes como C# y VB.NET . [59]
Véase también
Referencias
- ^ ab Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2009). Introducción a los algoritmos (3.ª ed.). Instituto Tecnológico de Massachusetts. págs. 253–280. ISBN 978-0-262-03384-8.
- ^ Mehlhorn, Kurt ; Sanders, Peter (2008). "Tablas hash y matrices asociativas" (PDF) . Algoritmos y estructuras de datos . Springer. págs. 81–98. doi :10.1007/978-3-540-77978-0_4. ISBN 978-3-540-77977-3.
- ^ Leiserson, Charles E. (otoño de 2005). "Conferencia 13: algoritmos amortizados, duplicación de tablas, método potencial". Curso MIT 6.046J/18.410J Introducción a los algoritmos . Archivado desde el original el 7 de agosto de 2009.
- ^ abc Knuth, Donald (1998). El arte de la programación informática . Vol. 3: Ordenación y búsqueda (2.ª ed.). Addison-Wesley. págs. 513–558. ISBN 978-0-201-89685-5.
- ^ Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2001). "Capítulo 11: Tablas hash". Introducción a los algoritmos (2.ª ed.). MIT Press y McGraw-Hill. págs. 221–252. ISBN 978-0-262-53196-2.
- ^ abcde Sedgewick, Robert ; Wayne, Kevin (2011). Algoritmos. Vol. 1 (4.ª ed.). Addison-Wesley Professional – a través de la Universidad de Princeton , Departamento de Ciencias de la Computación.
- ^ abc Konheim, Alan G. (2010). Hashing en informática . doi :10.1002/9780470630617. ISBN 978-0-470-34473-6.
- ^ abcdefghijklm Mehta, Dinesh P.; Mehta, Dinesh P.; Sahni, Sartaj, eds. (2004). Manual de estructuras de datos y aplicaciones . doi :10.1201/9781420035179. ISBN 978-0-429-14701-2.
- ^ abcdefg Mayers, Andrew (2008). «CS 312: Tablas hash y análisis amortizado». Universidad de Cornell , Departamento de Ciencias de la Computación. Archivado desde el original el 26 de abril de 2021. Consultado el 26 de octubre de 2021 en cs.cornell.edu.
- ^ por James S. Plank y Brad Vander Zanden. "Notas de clase de CS140: Hashing".
- ^ Maurer, WD; Lewis, TG (marzo de 1975). "Métodos de tabla hash". Encuestas de computación de ACM . 7 (1): 5–19. doi :10.1145/356643.356645. S2CID 17874775.
- ^ ab Owolabi, Olumide (febrero de 2003). "Estudios empíricos de algunas funciones hash". Tecnología de la información y el software . 45 (2): 109–112. doi :10.1016/S0950-5849(02)00174-X.
- ^ ab Lu, Yi; Prabhakar, Balaji; Bonomi, Flavio (2006). Hashing perfecto para aplicaciones de red . Simposio internacional IEEE sobre teoría de la información de 2006. págs. 2774–2778. doi :10.1109/ISIT.2006.261567. ISBN 1-4244-0505-X.S2CID 1494710 .
- ^ Belazzougui, Djamal; Botelho, Fabiano C.; Dietzfelbinger, Martin (2009). "Hash, displace, and compress" (PDF) . Algorithms—ESA 2009: 17th Annual European Symposium, Copenhague, Dinamarca, 7–9 de septiembre de 2009, Actas . Lecture Notes in Computer Science . Vol. 5757. Berlín: Springer. págs. 682–693. CiteSeerX 10.1.1.568.130 . doi :10.1007/978-3-642-04128-0_61. MR 2557794.
- ^ ab Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2001). "Capítulo 11: Tablas hash". Introducción a los algoritmos (2.ª ed.). Instituto Tecnológico de Massachusetts . ISBN 978-0-262-53196-2.
- ^ Pearson, Karl (1900). "Sobre el criterio de que un sistema dado de desviaciones de lo probable en el caso de un sistema correlacionado de variables es tal que puede suponerse razonablemente que ha surgido de un muestreo aleatorio". Philosophical Magazine . Serie 5. 50 (302): 157–175. doi :10.1080/14786440009463897.
- ^ Plackett, Robin (1983). "Karl Pearson y la prueba de chi-cuadrado". Revista estadística internacional . 51 (1): 59–72. doi :10.2307/1402731. JSTOR 1402731.
- ^ ab Wang, Thomas (marzo de 1997). «Prime Double Hash Table». Archivado desde el original el 3 de septiembre de 1999. Consultado el 10 de mayo de 2015 .
- ^ Wegman, Mark N.; Carter, J. Lawrence (junio de 1981). "Nuevas funciones hash y su uso en autenticación e igualdad de conjuntos". Journal of Computer and System Sciences . 22 (3): 265–279. doi : 10.1016/0022-0000(81)90033-7 .
- ^ abc Donald E. Knuth (24 de abril de 1998). El arte de la programación informática: volumen 3: Ordenación y búsqueda. Addison-Wesley Professional. ISBN 978-0-201-89685-5.
- ^ Demaine, Erik; Lind, Jeff (primavera de 2003). "Lecture 2" (PDF) . 6.897: Advanced Data Structures. Laboratorio de Ciencias de la Computación e Inteligencia Artificial del MIT . Archivado (PDF) desde el original el 15 de junio de 2010. Consultado el 30 de junio de 2008 .
- ^ abc Culpepper, J. Shane; Moffat, Alistair (2005). "Códigos de bytes mejorados con propiedades de prefijo restringidas". Procesamiento de cadenas y recuperación de información . Apuntes de clase en informática. Vol. 3772. págs. 1–12. doi :10.1007/11575832_1. ISBN 978-3-540-29740-6.
- ^ Willard, Dan E. (2000). "Examen de la geometría computacional, árboles de van Emde Boas y hash desde la perspectiva del árbol de fusión". Revista SIAM de Computación . 29 (3): 1030–1049. doi :10.1137/S0097539797322425. MR 1740562..
- ^ Askitis, Nikolas; Sinha, Ranjan (octubre de 2010). "Ingeniería de intentos escalables, eficientes en caché y en espacio para cadenas". The VLDB Journal . 19 (5): 633–660. doi :10.1007/s00778-010-0183-9.
- ^ Askitis, Nikolas; Zobel, Justin (octubre de 2005). "Resolución de colisiones consciente de la memoria caché en tablas hash de cadenas". Actas de la 12.ª Conferencia internacional sobre procesamiento de cadenas y recuperación de información (SPIRE 2005) . Vol. 3772/2005. págs. 91–102. doi :10.1007/11575832_11. ISBN 978-3-540-29740-6.
- ^ Askitis, Nikolas (2009). "Tablas hash rápidas y compactas para claves enteras" (PDF) . Actas de la 32.ª Conferencia de Ciencias Informáticas de Australasia (ACSC 2009) . Vol. 91. Págs. 113-122. ISBN. 978-1-920682-72-9. Archivado desde el original (PDF) el 16 de febrero de 2011 . Consultado el 13 de junio de 2010 .
- ^ Tenenbaum, Aaron M.; Langsam, Yedidyah; Augenstein, Moshe J. (1990). Estructuras de datos usando C. Prentice Hall. págs. 456–461, pág. 472.ISBN 978-0-13-199746-2.
- ^ ab Pagh, Rasmus ; Rodler, Flemming Friche (2001). "Hashing de cuco". Algoritmos: ESA 2001 . Apuntes de conferencias sobre informática. vol. 2161, págs. 121-133. CiteSeerX 10.1.1.25.4189 . doi :10.1007/3-540-44676-1_10. ISBN 978-3-540-42493-2.
- ^ abc Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2001), "11 tablas hash", Introducción a los algoritmos (2.ª ed.), MIT Press y McGraw-Hill , págs. 221–252, ISBN 0-262-03293-7.
- ^ abc Vitter, Jeffery S.; Chen, Wen-Chin (1987). El diseño y análisis del hash coalescido . Nueva York, Estados Unidos: Oxford University Press . ISBN 978-0-19-504182-8– vía Archive.org .
- ^ Pagh, Rasmus ; Rodler, Flemming Friche (2001). "Hashing de cuco". Algoritmos: ESA 2001 . Apuntes de conferencias sobre informática. vol. 2161, págs. 121-133. CiteSeerX 10.1.1.25.4189 . doi :10.1007/3-540-44676-1_10. ISBN 978-3-540-42493-2.
- ^ abcdef Herlihy, Maurice; Shavit, Nir; Tzafrir, Moran (2008). "Hopscotch Hashing". Computación distribuida . Apuntes de clase en informática. Vol. 5218. págs. 350–364. doi :10.1007/978-3-540-87779-0_24. ISBN 978-3-540-87778-3.
- ^ ab Celis, Pedro (1986). Hashing de Robin Hood (PDF) . Ontario, Canadá: Universidad de Waterloo , Departamento de Ciencias de la Computación. ISBN 978-0-315-29700-5. OCLC 14083698. Archivado (PDF) del original el 1 de noviembre de 2021 . Consultado el 2 de noviembre de 2021 .
- ^ Poblete, PV; Viola, A. (julio de 2019). "Análisis de Robin Hood y otros algoritmos hash bajo el modelo de sondeo aleatorio, con y sin deleciones". Combinatoria, probabilidad y computación . 28 (4): 600–617. doi :10.1017/S0963548318000408. S2CID 125374363.
- ^ Clarkson, Michael (2014). «Conferencia 13: Tablas hash». Universidad de Cornell , Departamento de Ciencias de la Computación. Archivado desde el original el 7 de octubre de 2021. Consultado el 1 de noviembre de 2021 en cs.cornell.edu.
- ^ Gries, David (2017). «JavaHyperText and Data Structure: Robin Hood Hashing» (PDF) . Universidad de Cornell , Departamento de Ciencias de la Computación. Archivado (PDF) del original el 26 de abril de 2021. Consultado el 2 de noviembre de 2021 en cs.cornell.edu.
- ^ Celis, Pedro (28 de marzo de 1988). External Robin Hood Hashing (PDF) (Informe técnico). Bloomington, Indiana: Indiana University , Departamento de Ciencias de la Computación. 246. Archivado (PDF) del original el 3 de noviembre de 2021. Consultado el 2 de noviembre de 2021 .
- ^ Goddard, Wayne (2021). «Capítulo C5: Tablas hash» (PDF) . Universidad de Clemson . pp. 15–16 . Consultado el 4 de diciembre de 2023 .
- ^ Devadas, Srini; Demaine, Erik (25 de febrero de 2011). «Introducción a los algoritmos: cambio de tamaño de las tablas hash» (PDF) . Instituto Tecnológico de Massachusetts , Departamento de Ciencias de la Computación. Archivado (PDF) del original el 7 de mayo de 2021. Consultado el 9 de noviembre de 2021 – vía MIT OpenCourseWare .
- ^ Thareja, Reema (2014). "Hashing y colisión". Estructuras de datos utilizando C. Oxford University Press. págs. 464–488. ISBN 978-0-19-809930-7.
- ^ ab Friedman, Scott; Krishnan, Anand; Leidefrost, Nicholas (18 de marzo de 2003). "Tablas hash para sistemas integrados y en tiempo real" (PDF) . Toda la investigación en ciencias de la computación e ingeniería . Universidad de Washington en St. Louis . doi :10.7936/K7WD3XXV. Archivado (PDF) del original el 9 de junio de 2021 . Consultado el 9 de noviembre de 2021 – a través de Northwestern University , Departamento de Ciencias de la Computación.
- ^ Litwin, Witold (1980). «Hash lineal: una nueva herramienta para el direccionamiento de archivos y tablas» (PDF) . Actas de la 6.ª Conferencia sobre bases de datos muy grandes . Universidad Carnegie Mellon . págs. 212–223. Archivado (PDF) del original el 6 de mayo de 2021. Consultado el 10 de noviembre de 2021 en cs.cmu.edu.
- ^ ab Dijk, Tom Van (2010). "Análisis y mejora del rendimiento de las tablas hash" (PDF) . Países Bajos : Universidad de Twente . Archivado (PDF) del original el 6 de noviembre de 2021. Consultado el 31 de diciembre de 2021 .
- ^ Lech Banachowski. "Índices y clasificación externa". pl:Polsko-Japońska Akademia Technik Komputerowych. Archivado desde el original el 26 de marzo de 2022 . Consultado el 26 de marzo de 2022 .
- ^ Zhong, Liang; Zheng, Xueqian; Liu, Yong; Wang, Mengting; Cao, Yang (febrero de 2020). "Maximización de la tasa de aciertos de caché en comunicaciones de dispositivo a dispositivo superpuestas a redes celulares". Comunicaciones de China . 17 (2): 232–238. doi :10.23919/jcc.2020.02.018. S2CID 212649328.
- ^ Bottommley, James (1 de enero de 2004). «Understanding Caching». Linux Journal . Archivado desde el original el 4 de diciembre de 2020. Consultado el 16 de abril de 2022 .
- ^ Jill Seaman (2014). "Set & Hash Tables" (PDF) . Universidad Estatal de Texas . Archivado desde el original el 1 de abril de 2022. Consultado el 26 de marzo de 2022 .
{{cite web}}: CS1 maint: bot: estado de URL original desconocido ( enlace ) - ^ "Tabla de transposición - Wiki de programación de ajedrez". chessprogramming.org . Archivado desde el original el 14 de febrero de 2021 . Consultado el 1 de mayo de 2020 .
- ^ "Tipos de datos y estructuras de datos de JavaScript - JavaScript | MDN". developer.mozilla.org . Consultado el 24 de julio de 2022 .
- ^ "Mapa - JavaScript | MDN". developer.mozilla.org . 20 de junio de 2023 . Consultado el 15 de julio de 2023 .
- ^ "Lenguaje de programación C++ - Especificación técnica" (PDF) . Organización Internacional de Normalización . págs. 812–813. Archivado desde el original (PDF) el 21 de enero de 2022 . Consultado el 8 de febrero de 2022 .
- ^ "La especificación del lenguaje de programación Go". go.dev . Consultado el 1 de enero de 2023 .
- ^ "Lección: Implementaciones (Tutoriales de Java™ > Colecciones)". docs.oracle.com . Archivado desde el original el 18 de enero de 2017 . Consultado el 27 de abril de 2018 .
- ^ Zhang, Juan; Jia, Yunwei (2020). "Optimización de rehash de Redis basada en aprendizaje automático". Journal of Physics: Conference Series . 1453 (1): 3. Bibcode :2020JPhCS1453a2048Z. doi : 10.1088/1742-6596/1453/1/012048 . S2CID 215943738.
- ^ Jonan Scheffler (25 de diciembre de 2016). «Lanzamiento de Ruby 2.4: hashes más rápidos, números enteros unificados y mejor redondeo». heroku.com . Archivado desde el original el 3 de julio de 2019. Consultado el 3 de julio de 2019 .
- ^ "doc.rust-lang.org". Archivado desde el original el 8 de diciembre de 2022 . Consultado el 14 de diciembre de 2022 .
- ^ "Clase HashSet (System.Collections.Generic)". learn.microsoft.com . Consultado el 1 de julio de 2023 .
- ^ dotnet-bot. «Clase de diccionario (System.Collections.Generic)». learn.microsoft.com . Consultado el 16 de enero de 2024 .
- ^ "Ejemplo de HashSet en VB.NET". Dot Net Perls .
Lectura adicional
- Tamassia, Roberto; Goodrich, Michael T. (2006). "Capítulo nueve: mapas y diccionarios". Estructuras de datos y algoritmos en Java: [actualizado para Java 5.0] (4.ª ed.). Hoboken, NJ: Wiley. págs. 369–418. ISBN 978-0-471-73884-8.
- McKenzie, BJ; Harries, R.; Bell, T. (febrero de 1990). "Selección de un algoritmo de hash". Software: práctica y experiencia . 20 (2): 209–224. doi :10.1002/spe.4380200207. hdl : 10092/9691 . S2CID 12854386.
Enlaces externos
- Entrada del NIST sobre tablas hash
- Estructuras de datos abiertas – Capítulo 5 – Tablas hash, Pat Morin
- Introducción a los algoritmos del MIT: Hashing 1 Vídeo de la conferencia MIT OCW
- Introducción a los algoritmos del MIT: Hashing 2 Vídeo de la conferencia MIT OCW





![{\displaystyle A[h(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac75d530b12267b829df7cff8b2ff01a24e61ab0)


























![{\displaystyle x.psl\ \leq \ T[j].psl}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0813eb6a21c2c8a817aa86085d3cf9417f01e8fb)
![{\displaystyle x.psl\ >\T[j].psl}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d06f4753fda641edd5afb066239100a667124f39)
![{\displaystyle T[j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb1f9ca1ed801caf88d5004aa3685644667099b6)








![{\displaystyle \mathrm {Tabla} [h_{\text{antiguo}}(\mathrm {clave} )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afcb195bb40a51be98c16b6d9b930061f3c11682)
![{\displaystyle \mathrm {Tabla} [h_{\text{nuevo}}(\mathrm {clave} )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8097baf3c9220a1be057b3c86395debce381845)





