Electrón

Electrón

Orbitales atómicos del hidrógeno en diferentes niveles de energía. Las zonas más opacas son aquellas en las que es más probable encontrar un electrón en un momento dado.
Composición	Partícula elemental [1]
Estadística	Fermiónico
Familia	Leptón
Generación	Primero
Interacciones	Débil , electromagnético , gravedad.
Símbolo	mi− , β−
Antipartícula	Positrón [a]
Teorizado	Richard Laming (1838–1851), [2] G. Johnstone Stoney (1874) y otros. [3] [4]
Descubierto	J. J. Thomson (1897) [5]
Masa	9.109 383 7139 (28) × 10 −31  kg ‍ [ 6] 5,485 799 090 441 (97) × 10 −4  Da ‍ [ 7] [1 822 , 888 486 209 (53) ] −1  Da [b] 0,510 998 950 69 (16)  MeV/ c2 [ 8 ]
Vida media	>6,6 × 10 28  años [9] (estable)
Carga eléctrica	−1  y −1.602 176 634 × 10 −19  C ‍ [ 10]
Momento magnético	−9,284 764 6917 (29) × 10 −24  J⋅T −1 ‍ [ 11] −1,001 159 652 181 28 (18)  µ B [12]
Girar	⁠ 1 /2⁠  ħ
Isospín débil	LH : − ⁠ 1 /2⁠ , DERECHA : 0
Hipercarga débil	LH : -1, DE : -2

Modelo estándar de física de partículas
Partículas elementales del Modelo Estándar
Fondo Física de partículas Modelo estándar Teoría cuántica de campos Teoría de gauge Ruptura espontánea de simetría Mecanismo de Higgs
Constituyentes Interacción electrodébil Cromodinámica cuántica Matriz CKM Matemáticas del Modelo Estándar
Limitaciones Strong CP problem Hierarchy problem Neutrino oscillations Physics beyond the Standard Model
Scientists Rutherford Thomson Chadwick Bose Sudarshan Davis Jr Anderson Fermi Dirac Feynman Rubbia Gell-Mann Kendall Taylor Friedman Powell Anderson Glashow Iliopoulos Lederman Maiani Meer Cowan Nambu Chamberlain Cabibbo Schwartz Perl Majorana Weinberg Lee Ward Salam Kobayashi Maskawa Mills Yang Yukawa 't Hooft Veltman Gross Pais Pauli Politzer Reines Schwinger Wilczek Cronin Fitch Vleck Higgs Englert Brout Hagen Guralnik Kibble de Mayolo Lattes Zweig
v t e

El electrón (
mi⁻
, o
β⁻
en reacciones nucleares) es una partícula subatómica con una carga eléctrica elemental negativa . ^[13] Los electrones pertenecen a la primera generación de la familia de partículas leptona , ^[14] y generalmente se piensa que son partículas elementales porque no tienen componentes o subestructura conocidos. ^{[1] La} masa del electrón es aproximadamente 1/1836 de la del protón . ^{[15] Las propiedades} mecánicas cuánticas del electrón incluyen un momento angular intrínseco ( espín ) de un valor medio entero, expresado en unidades de la constante de Planck reducida , ħ . Al ser fermiones , no hay dos electrones que puedan ocupar el mismo estado cuántico , según el principio de exclusión de Pauli . ^[14] Como todas las partículas elementales, los electrones exhiben propiedades tanto de partículas como de ondas : pueden colisionar con otras partículas y pueden difractarse como la luz. Las propiedades ondulatorias de los electrones son más fáciles de observar con experimentos que las de otras partículas como los neutrones y los protones porque los electrones tienen una masa menor y, por lo tanto, una longitud de onda de De Broglie más larga para una energía dada.

Los electrones desempeñan un papel esencial en numerosos fenómenos físicos , como la electricidad , el magnetismo , la química y la conductividad térmica ; también participan en interacciones gravitacionales , electromagnéticas y débiles . ^[16] Dado que un electrón tiene carga, tiene un campo eléctrico circundante ; si ese electrón se mueve en relación con un observador, el observador lo observará para generar un campo magnético . Los campos electromagnéticos producidos a partir de otras fuentes afectarán el movimiento de un electrón de acuerdo con la ley de fuerza de Lorentz . Los electrones irradian o absorben energía en forma de fotones cuando son acelerados.

Los instrumentos de laboratorio son capaces de atrapar electrones individuales, así como plasma de electrones mediante el uso de campos electromagnéticos. Los telescopios especiales pueden detectar plasma de electrones en el espacio exterior. Los electrones están involucrados en muchas aplicaciones, como la tribología o carga por fricción, la electrólisis, la electroquímica, las tecnologías de baterías, la electrónica , la soldadura , los tubos de rayos catódicos , la fotoelectricidad, los paneles solares fotovoltaicos, los microscopios electrónicos , la radioterapia , los láseres , los detectores de ionización gaseosa y los aceleradores de partículas .

Las interacciones que involucran a los electrones con otras partículas subatómicas son de interés en campos como la química y la física nuclear . La interacción de fuerza de Coulomb entre los protones positivos dentro de los núcleos atómicos y los electrones negativos fuera de ellos permite la composición de los dos conocidos como átomos . La ionización o las diferencias en las proporciones de electrones negativos versus núcleos positivos cambian la energía de enlace de un sistema atómico. El intercambio o compartición de los electrones entre dos o más átomos es la principal causa del enlace químico . ^[17]

En 1838, el filósofo natural británico Richard Laming formuló por primera vez la hipótesis del concepto de una cantidad indivisible de carga eléctrica para explicar las propiedades químicas de los átomos. ^[3] El físico irlandés George Johnstone Stoney denominó a esta carga "electrón" en 1891, y JJ Thomson y su equipo de físicos británicos la identificaron como una partícula en 1897 durante el experimento del tubo de rayos catódicos . ^[5]

Los electrones participan en reacciones nucleares , como la nucleosíntesis en las estrellas , donde se les conoce como partículas beta . Los electrones pueden crearse mediante la desintegración beta de isótopos radiactivos y en colisiones de alta energía, por ejemplo, cuando los rayos cósmicos entran en la atmósfera. La antipartícula del electrón se llama positrón ; es idéntica al electrón, excepto que lleva carga eléctrica de signo opuesto. Cuando un electrón choca con un positrón , ambas partículas pueden aniquilarse , produciendo fotones de rayos gamma .

Los antiguos griegos notaron que el ámbar atraía objetos pequeños cuando se frotaba con piel. Junto con los rayos , este fenómeno es una de las primeras experiencias registradas de la humanidad con la electricidad . ^[18] En su tratado de 1600 De Magnete , el científico inglés William Gilbert acuñó el término neolatino electrica , para referirse a aquellas sustancias con propiedades similares a las del ámbar que atraen objetos pequeños después de ser frotadas. ^[19] Tanto eléctrico como electricidad se derivan del latín ēlectrum (también la raíz de la aleación del mismo nombre ), que proviene de la palabra griega para ámbar, ἤλεκτρον ( ēlektron ).

A principios de la década de 1700, el químico francés Charles François du Fay descubrió que si una hoja de oro cargada es rechazada por el vidrio frotado con seda, entonces la misma hoja de oro cargada es atraída por el ámbar frotado con lana. A partir de este y otros resultados de tipos similares de experimentos, du Fay concluyó que la electricidad consta de dos fluidos eléctricos , el fluido vítreo del vidrio frotado con seda y el fluido resinoso del ámbar frotado con lana. Estos dos fluidos pueden neutralizarse entre sí cuando se combinan. ^{[19] [20]} El científico estadounidense Ebenezer Kinnersley más tarde también llegó de forma independiente a la misma conclusión. ^{[21] : 118} Una década después, Benjamin Franklin propuso que la electricidad no provenía de diferentes tipos de fluido eléctrico, sino de un solo fluido eléctrico que mostraba un exceso (+) o un déficit (−). Les dio la nomenclatura de carga moderna de positivo y negativo respectivamente. ^[22] Franklin pensó que el portador de carga era positivo, pero no identificó correctamente qué situación era un excedente del portador de carga y qué situación era un déficit. ^[23]

Entre 1838 y 1851, el filósofo natural británico Richard Laming desarrolló la idea de que un átomo está compuesto de un núcleo de materia rodeado de partículas subatómicas que tenían cargas eléctricas unitarias . ^[2] A partir de 1846, el físico alemán Wilhelm Eduard Weber teorizó que la electricidad estaba compuesta de fluidos cargados positiva y negativamente, y su interacción estaba regida por la ley del cuadrado inverso . Después de estudiar el fenómeno de la electrólisis en 1874, el físico irlandés George Johnstone Stoney sugirió que existía una "cantidad única y definida de electricidad", la carga de un ion monovalente . Pudo estimar el valor de esta carga elemental e mediante las leyes de electrólisis de Faraday . ^[24] Sin embargo, Stoney creía que estas cargas estaban permanentemente unidas a los átomos y no podían eliminarse. En 1881, el físico alemán Hermann von Helmholtz argumentó que tanto las cargas positivas como las negativas se dividían en partes elementales, cada una de las cuales "se comporta como átomos de electricidad". ^[3]

Stoney acuñó inicialmente el término electrón en 1881. Diez años después, cambió a electrón para describir estas cargas elementales, escribiendo en 1894: "... se hizo una estimación de la cantidad real de esta unidad fundamental de electricidad más notable, para la que desde entonces me he aventurado a sugerir el nombre de electrón ". Una propuesta de 1906 para cambiar a electrión fracasó porque Hendrik Lorentz prefirió mantener electrón . ^{[25] [26]} La palabra electrón es una combinación de las palabras electr ic e i on . ^[27] El sufijo -on que ahora se usa para designar otras partículas subatómicas, como un protón o un neutrón, se deriva a su vez de electrón. ^{[28] [29]}

En 1859, mientras estudiaba la conductividad eléctrica de los gases enrarecidos , el físico alemán Julius Plücker observó que la radiación emitida desde el cátodo hacía que apareciera una luz fosforescente en la pared del tubo cerca del cátodo; y la región de la luz fosforescente podía moverse mediante la aplicación de un campo magnético. ^[31] En 1869, el alumno de Plücker, Johann Wilhelm Hittorf, descubrió que un cuerpo sólido colocado entre el cátodo y la fosforescencia proyectaría una sombra sobre la región fosforescente del tubo. Hittorf dedujo que hay rayos rectos emitidos desde el cátodo y que la fosforescencia era causada por los rayos que golpeaban las paredes del tubo. Además, también descubrió que estos rayos son desviados por imanes al igual que las líneas de corriente. ^[32]

En 1876, el físico alemán Eugen Goldstein demostró que los rayos se emitían perpendicularmente a la superficie del cátodo, lo que distinguía entre los rayos que se emitían desde el cátodo y la luz incandescente. Goldstein denominó a los rayos rayos catódicos . ^{[33] [34] : 393} Décadas de investigación experimental y teórica que involucraron rayos catódicos fueron importantes en el eventual descubrimiento de los electrones por parte de JJ Thomson . ^[3] Goldstein también experimentó con cátodos dobles y planteó la hipótesis de que un rayo puede repeler a otro, aunque no creía que pudiera estar involucrada ninguna partícula. ^[35]

Durante la década de 1870, el químico y físico inglés Sir William Crookes desarrolló el primer tubo de rayos catódicos que tenía un alto vacío en su interior. ^[36] Luego, en 1874, demostró que los rayos catódicos pueden hacer girar una pequeña rueda de paletas cuando se colocan en su camino. Por lo tanto, concluyó que los rayos transportaban momento. Además, al aplicar un campo magnético, pudo desviar los rayos, demostrando así que el haz se comportaba como si estuviera cargado negativamente. ^[33] En 1879, propuso que estas propiedades podrían explicarse considerando que los rayos catódicos están compuestos de moléculas gaseosas cargadas negativamente en un cuarto estado de la materia en el que el camino libre medio de las partículas es tan largo que las colisiones pueden ignorarse. ^{[34] : 394–395}

En 1883, el todavía poco conocido físico alemán Heinrich Hertz intentó demostrar que los rayos catódicos son eléctricamente neutros y obtuvo lo que interpretó como una ausencia segura de deflexión en el campo electrostático, a diferencia del campo magnético. Sin embargo, como explicó JJ Thomson en 1897, Hertz colocó los electrodos deflectores en una zona altamente conductora del tubo, lo que dio como resultado un fuerte efecto de apantallamiento cerca de su superficie. ^[35]

El físico británico nacido en Alemania Arthur Schuster amplió los experimentos de Crookes colocando placas de metal paralelas a los rayos catódicos y aplicando un potencial eléctrico entre las placas. ^[37] El campo desvió los rayos hacia la placa cargada positivamente, proporcionando más evidencia de que los rayos llevaban carga negativa. Al medir la cantidad de desviación para un campo eléctrico y magnético dado , en 1890 Schuster pudo estimar la relación carga-masa ^[c] de los componentes del rayo. Sin embargo, esto produjo un valor que era más de mil veces mayor que lo esperado, por lo que se le dio poco crédito a sus cálculos en ese momento. ^[33] Esto se debe a que se asumió que los portadores de carga eran átomos de hidrógeno o nitrógeno mucho más pesados . ^[37] Las estimaciones de Schuster posteriormente resultarían ser en gran medida correctas.

En 1892 Hendrik Lorentz sugirió que la masa de estas partículas (electrones) podría ser una consecuencia de su carga eléctrica. ^[38]

En 1896, mientras estudiaba minerales fluorescentes naturales, el físico francés Henri Becquerel descubrió que emitían radiación sin exposición a una fuente de energía externa. Estos materiales radiactivos se convirtieron en objeto de mucho interés para los científicos, incluido el físico neozelandés Ernest Rutherford, quien descubrió que emitían partículas. Designó a estas partículas alfa y beta , basándose en su capacidad para penetrar la materia. ^[39] En 1900, Becquerel demostró que los rayos beta emitidos por el radio podían ser desviados por un campo eléctrico y que su relación masa-carga era la misma que la de los rayos catódicos. ^[40] Esta evidencia fortaleció la idea de que los electrones existían como componentes de los átomos. ^{[41] [42]}

En 1897, el físico británico JJ Thomson , con sus colegas John S. Townsend y HA Wilson , realizó experimentos que indicaban que los rayos catódicos eran realmente partículas únicas, en lugar de ondas, átomos o moléculas como se creía anteriormente. ^[5] En 1899 demostró que su relación carga-masa, e / m , era independiente del material del cátodo. Demostró además que las partículas cargadas negativamente producidas por materiales radiactivos, por materiales calentados y por materiales iluminados eran universales. ^{[5] [43]} Thomson midió m / e para los "corpúsculos" de rayos catódicos, e hizo buenas estimaciones de la carga e , lo que llevó a un valor para la masa m , encontrando un valor 1400 veces menos masivo que el ion menos masivo conocido: el hidrógeno. ^{[34] : 364  [5]} En el mismo año, Emil Wiechert y Walter Kaufmann también calcularon la relación e / m , pero no dieron el paso de interpretar sus resultados como si mostraran una nueva partícula, mientras que JJ Thomson posteriormente en 1899 daría estimaciones para la carga y la masa del electrón también: e  ~ 6,8 × 10 ⁻¹⁰  esu y m  ~ 3 × 10 ⁻²⁶  g ^{[44] [45]}

El nombre "electrón" fue adoptado para estas partículas por la comunidad científica, principalmente debido a la defensa de GF FitzGerald , J. Larmor y HA Lorentz . ^{[46] : 273} El término fue acuñado originalmente por George Johnstone Stoney en 1891 como un nombre tentativo para la unidad básica de carga eléctrica (que aún no se había descubierto). ^{[47] [26]}

La carga del electrón fue medida con más cuidado por los físicos estadounidenses Robert Millikan y Harvey Fletcher en su experimento de la gota de aceite de 1909, cuyos resultados se publicaron en 1911. Este experimento utilizó un campo eléctrico para evitar que una gota de aceite cargada cayera como resultado de la gravedad. Este dispositivo podía medir la carga eléctrica de tan solo 1 a 150 iones con un margen de error de menos del 0,3%. Experimentos comparables habían sido realizados anteriormente por el equipo de Thomson ^[5] , utilizando nubes de gotas de agua cargadas generadas por electrólisis, y en 1911 por Abram Ioffe , quien obtuvo independientemente el mismo resultado que Millikan utilizando micropartículas cargadas de metales, luego publicó sus resultados en 1913. ^[48] Sin embargo, las gotas de aceite eran más estables que las gotas de agua debido a su tasa de evaporación más lenta y, por lo tanto, más adecuadas para la experimentación precisa durante períodos de tiempo más largos. ^[49]

A principios del siglo XX se descubrió que, en determinadas condiciones, una partícula cargada que se desplazaba rápidamente provocaba una condensación de vapor de agua sobresaturado a lo largo de su trayectoria. En 1911, Charles Wilson utilizó este principio para diseñar su cámara de niebla, de modo que pudiera fotografiar las trayectorias de partículas cargadas, como los electrones que se desplazaban rápidamente. ^[50]

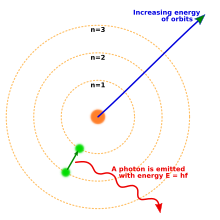
En 1914, los experimentos de los físicos Ernest Rutherford , Henry Moseley , James Franck y Gustav Hertz habían establecido en gran medida la estructura de un átomo como un núcleo denso de carga positiva rodeado de electrones de menor masa. ^[51] En 1913, el físico danés Niels Bohr postuló que los electrones residían en estados de energía cuantizados, con sus energías determinadas por el momento angular de la órbita del electrón alrededor del núcleo. Los electrones podían moverse entre esos estados, u órbitas, por la emisión o absorción de fotones de frecuencias específicas. Por medio de estas órbitas cuantizadas, explicó con precisión las líneas espectrales del átomo de hidrógeno. ^[52] Sin embargo, el modelo de Bohr no tuvo en cuenta las intensidades relativas de las líneas espectrales y no tuvo éxito en la explicación de los espectros de átomos más complejos. ^[51]

Los enlaces químicos entre átomos fueron explicados por Gilbert Newton Lewis , quien en 1916 propuso que un enlace covalente entre dos átomos se mantiene por un par de electrones compartidos entre ellos. ^[53] Más tarde, en 1927, Walter Heitler y Fritz London dieron la explicación completa de la formación de pares de electrones y el enlace químico en términos de mecánica cuántica . ^[54] En 1919, el químico estadounidense Irving Langmuir elaboró ​​​​el modelo estático del átomo de Lewis y sugirió que todos los electrones se distribuían en sucesivas "capas concéntricas (casi) esféricas, todas de igual espesor". ^[55] A su vez, dividió las capas en una serie de celdas cada una de las cuales contenía un par de electrones. Con este modelo Langmuir pudo explicar cualitativamente las propiedades químicas de todos los elementos de la tabla periódica, ^[54] que se sabía que se repetían en gran medida de acuerdo con la ley periódica . ^[56]

En 1924, el físico austríaco Wolfgang Pauli observó que la estructura en forma de capa del átomo podía explicarse mediante un conjunto de cuatro parámetros que definían cada estado de energía cuántica, siempre que cada estado estuviera ocupado por no más de un electrón. Esta prohibición de que más de un electrón ocupara el mismo estado de energía cuántica se conoció como el principio de exclusión de Pauli . ^[57] El mecanismo físico para explicar el cuarto parámetro, que tenía dos posibles valores distintos, fue proporcionado por los físicos holandeses Samuel Goudsmit y George Uhlenbeck . En 1925, sugirieron que un electrón, además del momento angular de su órbita, posee un momento angular intrínseco y un momento dipolar magnético . ^{[51] [58]} Esto es análogo a la rotación de la Tierra sobre su eje mientras orbita alrededor del Sol. El momento angular intrínseco se conoció como espín y explicó la división previamente misteriosa de las líneas espectrales observadas con un espectrógrafo de alta resolución ; este fenómeno se conoce como división de estructura fina . ^[59]

En su disertación de 1924 Recherches sur la théorie des quanta (Investigación sobre la teoría cuántica), el físico francés Louis de Broglie planteó la hipótesis de que toda la materia puede representarse como una onda de De Broglie a la manera de la luz . ^[60] Es decir, en las condiciones apropiadas, los electrones y otra materia mostrarían propiedades de partículas u ondas. Las propiedades corpusculares de una partícula se demuestran cuando se muestra que tiene una posición localizada en el espacio a lo largo de su trayectoria en un momento dado. ^[61] La naturaleza ondulatoria de la luz se muestra, por ejemplo, cuando un haz de luz pasa a través de rendijas paralelas creando así patrones de interferencia . En 1927, George Paget Thomson y Alexander Reid descubrieron que el efecto de interferencia se producía cuando un haz de electrones pasaba a través de láminas delgadas de celuloide y más tarde películas de metal, y por los físicos estadounidenses Clinton Davisson y Lester Germer por la reflexión de electrones de un cristal de níquel . ^[62] Alexander Reid, quien fue estudiante de posgrado de Thomson, realizó los primeros experimentos, pero murió poco después en un accidente de motocicleta ^[63] y rara vez se lo menciona.

La predicción de De Broglie de una naturaleza ondulatoria para los electrones llevó a Erwin Schrödinger a postular una ecuación de onda para los electrones que se movían bajo la influencia del núcleo del átomo. En 1926, esta ecuación, la ecuación de Schrödinger , describió con éxito cómo se propagaban las ondas de electrones. ^[64] En lugar de producir una solución que determinara la ubicación de un electrón a lo largo del tiempo, esta ecuación de onda también podría usarse para predecir la probabilidad de encontrar un electrón cerca de una posición, especialmente una posición cerca de donde el electrón estaba ligado en el espacio, para la cual las ecuaciones de onda del electrón no cambiaban en el tiempo. Este enfoque condujo a una segunda formulación de la mecánica cuántica (la primera por Heisenberg en 1925), y las soluciones de la ecuación de Schrödinger, como la de Heisenberg, proporcionaron derivaciones de los estados de energía de un electrón en un átomo de hidrógeno que eran equivalentes a los que habían sido derivados primero por Bohr en 1913, y que se sabía que reproducían el espectro del hidrógeno. ^[65] Una vez que el espín y la interacción entre múltiples electrones fueron descriptibles, la mecánica cuántica hizo posible predecir la configuración de los electrones en átomos con números atómicos mayores que el hidrógeno. ^[66]

En 1928, basándose en el trabajo de Wolfgang Pauli, Paul Dirac produjo un modelo del electrón, la ecuación de Dirac , consistente con la teoría de la relatividad , al aplicar consideraciones relativistas y de simetría a la formulación hamiltoniana de la mecánica cuántica del campo electromagnético. ^[67] Para resolver algunos problemas dentro de su ecuación relativista, Dirac desarrolló en 1930 un modelo del vacío como un mar infinito de partículas con energía negativa, más tarde llamado mar de Dirac . Esto lo llevó a predecir la existencia de un positrón, la contraparte de antimateria del electrón. ^[68] Esta partícula fue descubierta en 1932 por Carl Anderson , quien propuso llamar negatrones a los electrones estándar y usar electrón como un término genérico para describir las variantes cargadas positiva y negativamente. ^[69]

En 1947, Willis Lamb , trabajando en colaboración con el estudiante de posgrado Robert Retherford , descubrió que ciertos estados cuánticos del átomo de hidrógeno, que deberían tener la misma energía, estaban desplazados entre sí; la diferencia pasó a llamarse desplazamiento de Lamb . Casi al mismo tiempo, Polykarp Kusch , trabajando con Henry M. Foley , descubrió que el momento magnético del electrón es ligeramente mayor que el predicho por la teoría de Dirac. Esta pequeña diferencia se denominó más tarde momento dipolar magnético anómalo del electrón. Esta diferencia fue explicada más tarde por la teoría de la electrodinámica cuántica , desarrollada por Sin-Itiro Tomonaga , Julian Schwinger y Richard Feynman a fines de la década de 1940. ^[70]

Con el desarrollo del acelerador de partículas durante la primera mitad del siglo XX, los físicos comenzaron a profundizar en las propiedades de las partículas subatómicas . ^[71] El primer intento exitoso de acelerar electrones usando inducción electromagnética fue realizado en 1942 por Donald Kerst . Su betatrón inicial alcanzó energías de 2,3 MeV, mientras que los betatrones posteriores lograron 300 MeV. En 1947, se descubrió la radiación de sincrotrón con un sincrotrón de electrones de 70 MeV en General Electric . Esta radiación fue causada por la aceleración de los electrones a través de un campo magnético mientras se movían cerca de la velocidad de la luz. ^[72]

Con una energía de haz de 1,5 GeV, el primer colisionador de partículas de alta energía fue ADONE , que comenzó a operar en 1968. ^[73] Este dispositivo aceleró electrones y positrones en direcciones opuestas, duplicando efectivamente la energía de su colisión en comparación con golpear un objetivo estático con un electrón. ^[74] El Gran Colisionador de Electrones y Positrones (LEP) en el CERN , que estuvo operativo desde 1989 hasta 2000, alcanzó energías de colisión de 209 GeV y realizó mediciones importantes para el Modelo Estándar de física de partículas. ^{[75] [76]}

Los electrones individuales ahora se pueden confinar fácilmente en transistores CMOS  ultra pequeños ( L = 20 nm , W = 20 nm ) operados a temperatura criogénica en un rango de −269 °C (4 K ) a aproximadamente −258 °C (15  K ). ^[77] La ​​función de onda del electrón se propaga en una red de semiconductores e interactúa de manera despreciable con los electrones de la banda de valencia, por lo que se puede tratar en el formalismo de partícula única, reemplazando su masa con el tensor de masa efectivo .

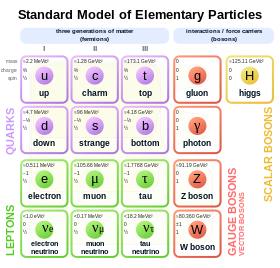
En el Modelo Estándar de la física de partículas, los electrones pertenecen al grupo de partículas subatómicas llamadas leptones , que se cree que son partículas fundamentales o elementales . Los electrones tienen la masa más baja de cualquier leptón cargado (o partícula cargada eléctricamente de cualquier tipo) y pertenecen a la primera generación de partículas fundamentales. ^[78] La segunda y tercera generación contienen leptones cargados, el muón y el tau , que son idénticos al electrón en carga, espín e interacciones , pero son más masivos. Los leptones se diferencian del otro constituyente básico de la materia, los quarks , por su falta de interacción fuerte . Todos los miembros del grupo de los leptones son fermiones porque todos tienen espín entero medio impar; el electrón tiene espín ⁠1/2⁠ . ^[79]

La masa invariante de un electrón es aproximadamente9,109 × 10 ⁻³¹  kg , ^[80] o5,489 × 10 ⁻⁴  Da . Debido a la equivalencia masa-energía , esto corresponde a una energía en reposo de 0,511 MeV (8,19 × 10 ⁻¹⁴  J) . La relación entre la masa de un protón y la de un electrón es de aproximadamente 1836. ^{[15] [81]} Las mediciones astronómicas muestran que la relación de masas entre protones y electrones ha mantenido el mismo valor, como predice el Modelo Estándar, durante al menos la mitad de la edad del universo . ^[82]

Los electrones tienen una carga eléctrica de−1,602 176 634 × 10 ⁻¹⁹ culombios , ^[80] que se utiliza como unidad estándar de carga para partículas subatómicas, y también se denomina carga elemental . Dentro de los límites de la precisión experimental, la carga del electrón es idéntica a la carga de un protón, pero con el signo opuesto. ^[83] El electrón se simboliza comúnmente por
mi⁻
, y el positrón está simbolizado por
mi⁺
. ^{[79] [80]}

El electrón tiene un momento angular intrínseco o espín de ⁠Yo/2⁠ . ^[80] Esta propiedad se suele expresar haciendo referencia al electrón como una partícula de espín 1/2 . ^[79] Para tales partículas, la magnitud del espín es ⁠Yo/2⁠ , ^[84] mientras que el resultado de la medición de una proyección del espín sobre cualquier eje sólo puede ser ± ⁠Yo/2⁠ . Además del espín, el electrón tiene un momento magnético intrínseco a lo largo de su eje de espín. ^[80] Es aproximadamente igual a un magnetón de Bohr , ^{[85] [d]} que es una constante física que es igual a9.274 010 0657 (29) × 10 ⁻²⁴  J⋅T ⁻¹ . ^[86] La orientación del espín con respecto al momento del electrón define la propiedad de las partículas elementales conocida como helicidad . ^[87]

El electrón no tiene una subestructura conocida . ^{[1] [88]} Sin embargo, en la física de la materia condensada , la separación de espín y carga puede ocurrir en algunos materiales. En tales casos, los electrones se 'dividen' en tres partículas independientes, el espinón , el orbitón y el holón (o chargon). El electrón siempre puede considerarse teóricamente como un estado ligado de los tres, con el espinón llevando el espín del electrón, el orbitón llevando el grado de libertad orbital y el chargon llevando la carga, pero en ciertas condiciones pueden comportarse como cuasipartículas independientes . ^{[89] [90] [91]}

La cuestión del radio del electrón es un problema desafiante de la física teórica moderna. La admisión de la hipótesis de un radio finito del electrón es incompatible con las premisas de la teoría de la relatividad. Por otra parte, un electrón puntual (radio cero) genera serias dificultades matemáticas debido a que la energía propia del electrón tiende al infinito. ^[92] La observación de un solo electrón en una trampa de Penning sugiere que el límite superior del radio de la partícula es de 10 ⁻²²  metros. ^[93] El límite superior del radio del electrón de 10 ⁻¹⁸  metros ^[94] se puede derivar utilizando la relación de incertidumbre en energía. También existe una constante física llamada " radio electrónico clásico ", con el valor mucho mayor de2,8179 × 10 ⁻¹⁵  m , mayor que el radio del protón. Sin embargo, la terminología proviene de un cálculo simplista que ignora los efectos de la mecánica cuántica ; en realidad, el llamado radio clásico del electrón tiene poco que ver con la verdadera estructura fundamental del electrón. ^{[95] [96] [e]}

Existen partículas elementales que se desintegran espontáneamente en partículas menos masivas. Un ejemplo es el muón , con una vida media de2,2 × 10 ⁻⁶  segundos, que se desintegra en un electrón, un neutrino muónico y un antineutrino electrónico . Por otra parte, se cree que el electrón es estable por razones teóricas: el electrón es la partícula menos masiva con carga eléctrica distinta de cero, por lo que su desintegración violaría la conservación de la carga . ^[97] El límite inferior experimental para la vida media del electrón es6,6 × 10 ²⁸ años, con un nivel de confianza del 90% . ^{[9] [98] [99]}

Al igual que todas las partículas, los electrones pueden actuar como ondas. Esto se denomina dualidad onda-partícula y se puede demostrar mediante el experimento de la doble rendija .

La naturaleza ondulatoria del electrón le permite pasar a través de dos rendijas paralelas simultáneamente, en lugar de solo una rendija como sería el caso de una partícula clásica. En mecánica cuántica, la propiedad ondulatoria de una partícula se puede describir matemáticamente como una función de valor complejo , la función de onda , comúnmente denotada por la letra griega psi ( ψ ). Cuando el valor absoluto de esta función se eleva al cuadrado , da la probabilidad de que una partícula sea observada cerca de una ubicación: una densidad de probabilidad . ^{[100] : 162–218}

Los electrones son partículas idénticas porque no se pueden distinguir entre sí por sus propiedades físicas intrínsecas. En mecánica cuántica, esto significa que un par de electrones que interactúan deben poder intercambiar posiciones sin un cambio observable en el estado del sistema. La función de onda de los fermiones, incluidos los electrones, es antisimétrica, lo que significa que cambia de signo cuando se intercambian dos electrones; es decir, ψ ( r ₁ , r ₂ ) = − ψ ( r ₂ , r ₁ ) , donde las variables r ₁ y r ₂ corresponden al primer y segundo electrón, respectivamente. Dado que el valor absoluto no cambia con un intercambio de signos, esto corresponde a probabilidades iguales. Los bosones , como el fotón, tienen funciones de onda simétricas en cambio. ^{[100] : 162–218}

En el caso de la antisimetría, las soluciones de la ecuación de onda para los electrones en interacción dan como resultado una probabilidad cero de que cada par ocupe la misma ubicación o estado. Esto es responsable del principio de exclusión de Pauli , que impide que dos electrones cualesquiera ocupen el mismo estado cuántico. Este principio explica muchas de las propiedades de los electrones. Por ejemplo, hace que los grupos de electrones ligados ocupen diferentes orbitales en un átomo, en lugar de superponerse todos entre sí en la misma órbita. ^{[100] : 162–218}

En una imagen simplificada, que a menudo tiende a dar una idea equivocada pero que puede servir para ilustrar algunos aspectos, cada fotón pasa algún tiempo como una combinación de un electrón virtual más su antipartícula, el positrón virtual, que se aniquilan rápidamente entre sí poco después. ^[101] La combinación de la variación de energía necesaria para crear estas partículas, y el tiempo durante el cual existen, cae por debajo del umbral de detectabilidad expresado por la relación de incertidumbre de Heisenberg , Δ E  · Δ t  ≥  ħ . En efecto, la energía necesaria para crear estas partículas virtuales, Δ E , puede ser "tomada prestada" del vacío durante un período de tiempo, Δ t , de modo que su producto no sea más que la constante de Planck reducida , ħ ≈6,6 × 10 ⁻¹⁶  eV·s . Por lo tanto, para un electrón virtual, Δ t es como máximo1,3 × 10 ⁻²¹  s . ^[102]

Mientras existe un par virtual electrón-positrón, la fuerza de Coulomb del campo eléctrico ambiental que rodea a un electrón hace que un positrón creado sea atraído por el electrón original, mientras que un electrón creado experimenta una repulsión. Esto causa lo que se llama polarización del vacío . En efecto, el vacío se comporta como un medio que tiene una permitividad dieléctrica mayor que la unidad . Por lo tanto, la carga efectiva de un electrón es en realidad menor que su valor verdadero, y la carga disminuye a medida que aumenta la distancia desde el electrón. ^{[103] [104]} Esta polarización se confirmó experimentalmente en 1997 utilizando el acelerador de partículas japonés TRISTAN . ^[105] Las partículas virtuales causan un efecto de protección comparable para la masa del electrón. ^[106]

La interacción con partículas virtuales también explica la pequeña desviación (alrededor del 0,1%) del momento magnético intrínseco del electrón respecto del magnetón de Bohr (el momento magnético anómalo ). ^{[85] [107]} La ​​concordancia extraordinariamente precisa de esta diferencia predicha con el valor determinado experimentalmente se considera uno de los grandes logros de la electrodinámica cuántica . ^[108]

La aparente paradoja en la física clásica de un electrón como partícula puntual que tiene un momento angular y un momento magnético intrínsecos se puede explicar por la formación de fotones virtuales en el campo eléctrico generado por el electrón. Se puede pensar heurísticamente que estos fotones hacen que el electrón se desplace de manera inestable (conocido como zitterbewegung ), lo que resulta en un movimiento circular neto con precesión . ^[109] Este movimiento produce tanto el espín como el momento magnético del electrón. ^[14] En los átomos, esta creación de fotones virtuales explica el desplazamiento de Lamb observado en las líneas espectrales . ^[103] La longitud de onda Compton muestra que cerca de partículas elementales como el electrón, la incertidumbre de la energía permite la creación de partículas virtuales cerca del electrón. Esta longitud de onda explica la "estática" de las partículas virtuales alrededor de partículas elementales a una distancia cercana.

Un electrón genera un campo eléctrico que ejerce una fuerza de atracción sobre una partícula con carga positiva, como el protón, y una fuerza de repulsión sobre una partícula con carga negativa. La intensidad de esta fuerza en una aproximación no relativista está determinada por la ley del cuadrado inverso de Coulomb . ^{[110] : 58–61} Cuando un electrón está en movimiento, genera un campo magnético . ^{[100] : 140} La ley de Ampère-Maxwell relaciona el campo magnético con el movimiento de masa de los electrones (la corriente ) con respecto a un observador. Esta propiedad de inducción proporciona el campo magnético que impulsa un motor eléctrico . ^[111] El campo electromagnético de una partícula cargada en movimiento arbitrario se expresa mediante los potenciales de Liénard-Wiechert , que son válidos incluso cuando la velocidad de la partícula es cercana a la de la luz ( relativista ). ^{[110] : 429–434}

Cuando un electrón se mueve a través de un campo magnético, está sujeto a la fuerza de Lorentz que actúa perpendicularmente al plano definido por el campo magnético y la velocidad del electrón. Esta fuerza centrípeta hace que el electrón siga una trayectoria helicoidal a través del campo en un radio llamado radio de giro . La aceleración de este movimiento curvo induce al electrón a irradiar energía en forma de radiación de sincrotrón. ^{[112] [f] [100] : 160} La emisión de energía a su vez provoca un retroceso del electrón, conocido como Fuerza de Abraham-Lorentz-Dirac , que crea una fricción que frena al electrón. Esta fuerza es causada por una reacción inversa del propio campo del electrón sobre sí mismo. ^[113]

Los fotones median las interacciones electromagnéticas entre partículas en la electrodinámica cuántica . Un electrón aislado a una velocidad constante no puede emitir ni absorber un fotón real; al hacerlo, violaría la conservación de la energía y el momento . En cambio, los fotones virtuales pueden transferir momento entre dos partículas cargadas. Este intercambio de fotones virtuales, por ejemplo, genera la fuerza de Coulomb. ^[114] La emisión de energía puede ocurrir cuando un electrón en movimiento es desviado por una partícula cargada, como un protón. La desaceleración del electrón da como resultado la emisión de radiación de frenado . ^[115]

Una colisión inelástica entre un fotón (luz) y un electrón solitario (libre) se denomina dispersión Compton . Esta colisión da como resultado una transferencia de momento y energía entre las partículas, lo que modifica la longitud de onda del fotón en una cantidad llamada desplazamiento Compton . ^[g] La magnitud máxima de este desplazamiento de longitud de onda es h / m _e c , que se conoce como longitud de onda Compton . ^[116] Para un electrón, tiene un valor de2,43 × 10 ⁻¹²  m . ^[80] Cuando la longitud de onda de la luz es larga (por ejemplo, la longitud de onda de la luz visible es de 0,4–0,7 μm), el desplazamiento de la longitud de onda se vuelve insignificante. Esta interacción entre la luz y los electrones libres se denomina dispersión de Thomson o dispersión de Thomson lineal. ^[117]

La fuerza relativa de la interacción electromagnética entre dos partículas cargadas, como un electrón y un protón, está dada por la constante de estructura fina . Este valor es una cantidad adimensional formada por la relación de dos energías: la energía electrostática de atracción (o repulsión) a una separación de una longitud de onda Compton, y la energía en reposo de la carga. Está dada por α  ≈ 0,007 297 353 , ^[118] que es aproximadamente igual a ⁠1/137⁠ .

Cuando los electrones y los positrones chocan, se aniquilan entre sí, dando lugar a dos o más fotones de rayos gamma. Si el electrón y el positrón tienen un momento insignificante, se puede formar un átomo de positronio antes de que la aniquilación dé como resultado dos o tres fotones de rayos gamma que suman 1,022 MeV. ^{[119] [120]} Por otro lado, un fotón de alta energía puede transformarse en un electrón y un positrón mediante un proceso llamado producción de pares , pero solo en presencia de una partícula cargada cercana, como un núcleo. ^{[121] [122]}

En la teoría de la interacción electrodébil , el componente levógiro de la función de onda del electrón forma un doblete de isospín débil con el neutrino electrónico . Esto significa que durante las interacciones débiles , los neutrinos electrónicos se comportan como electrones. Cualquier miembro de este doblete puede experimentar una interacción de corriente cargada emitiendo o absorbiendo una
Yo
y convertirse en el otro miembro. La carga se conserva durante esta reacción porque el bosón W también lleva una carga, cancelando cualquier cambio neto durante la transmutación. Las interacciones de corriente cargada son responsables del fenómeno de la desintegración beta en un átomo radiactivo . Tanto el electrón como el neutrino electrónico pueden experimentar una interacción de corriente neutra a través de un
O⁰
intercambio, y esto es responsable de la dispersión elástica neutrino-electrón . ^[123]

Un electrón puede unirse al núcleo de un átomo mediante la fuerza de atracción de Coulomb. Un sistema de uno o más electrones unidos a un núcleo se denomina átomo. Si el número de electrones es diferente de la carga eléctrica del núcleo, dicho átomo se denomina ion . El comportamiento ondulatorio de un electrón unido se describe mediante una función llamada orbital atómico . Cada orbital tiene su propio conjunto de números cuánticos, como energía, momento angular y proyección del momento angular, y solo existe un conjunto discreto de estos orbitales alrededor del núcleo. Según el principio de exclusión de Pauli, cada orbital puede estar ocupado por hasta dos electrones, que deben diferir en su número cuántico de espín .

Los electrones pueden transferirse entre diferentes orbitales mediante la emisión o absorción de fotones con una energía que coincide con la diferencia de potencial. ^{[124] : 159–160} Otros métodos de transferencia orbital incluyen colisiones con partículas, como electrones, y el efecto Auger . ^[125] Para escapar del átomo, la energía del electrón debe aumentarse por encima de su energía de enlace con el átomo. Esto ocurre, por ejemplo, con el efecto fotoeléctrico , donde un fotón incidente que excede la energía de ionización del átomo es absorbido por el electrón. ^{[124] : 127–132}

El momento angular orbital de los electrones está cuantizado . Como el electrón está cargado, produce un momento magnético orbital que es proporcional al momento angular. El momento magnético neto de un átomo es igual a la suma vectorial de los momentos magnéticos orbitales y de espín de todos los electrones y del núcleo. El momento magnético del núcleo es insignificante comparado con el de los electrones. Los momentos magnéticos de los electrones que ocupan el mismo orbital, llamados electrones apareados, se cancelan entre sí. ^[126]

El enlace químico entre átomos se produce como resultado de interacciones electromagnéticas, como se describe en las leyes de la mecánica cuántica. ^[127] Los enlaces más fuertes se forman mediante la compartición o transferencia de electrones entre átomos, lo que permite la formación de moléculas . ^[17] Dentro de una molécula, los electrones se mueven bajo la influencia de varios núcleos y ocupan orbitales moleculares ; de la misma manera que pueden ocupar orbitales atómicos en átomos aislados. ^[128] Un factor fundamental en estas estructuras moleculares es la existencia de pares de electrones . Estos son electrones con espines opuestos, lo que les permite ocupar el mismo orbital molecular sin violar el principio de exclusión de Pauli (muy parecido a lo que ocurre en los átomos). Diferentes orbitales moleculares tienen una distribución espacial diferente de la densidad electrónica. Por ejemplo, en pares enlazados (es decir, en los pares que realmente unen a los átomos) los electrones se pueden encontrar con la máxima probabilidad en un volumen relativamente pequeño entre los núcleos. Por el contrario, en pares no enlazados los electrones se distribuyen en un gran volumen alrededor de los núcleos. ^[129]

Si un cuerpo tiene más o menos electrones de los necesarios para equilibrar la carga positiva de los núcleos, entonces ese objeto tiene una carga eléctrica neta. Cuando hay un exceso de electrones, se dice que el objeto está cargado negativamente. Cuando hay menos electrones que el número de protones en los núcleos, se dice que el objeto está cargado positivamente. Cuando el número de electrones y el número de protones son iguales, sus cargas se cancelan entre sí y se dice que el objeto es eléctricamente neutro. Un cuerpo macroscópico puede desarrollar una carga eléctrica a través del roce, por el efecto triboeléctrico . ^[133]

Los electrones independientes que se mueven en el vacío se denominan electrones libres . Los electrones en los metales también se comportan como si fueran libres. En realidad, las partículas que comúnmente se denominan electrones en los metales y otros sólidos son cuasielectrones, cuasipartículas , que tienen la misma carga eléctrica, espín y momento magnético que los electrones reales, pero pueden tener una masa diferente. ^[134] Cuando los electrones libres, tanto en el vacío como en los metales, se mueven, producen un flujo neto de carga llamado corriente eléctrica , que genera un campo magnético. Del mismo modo, una corriente puede ser creada por un campo magnético cambiante. Estas interacciones se describen matemáticamente mediante las ecuaciones de Maxwell . ^[135]

A una temperatura dada, cada material tiene una conductividad eléctrica que determina el valor de la corriente eléctrica cuando se aplica un potencial eléctrico . Ejemplos de buenos conductores incluyen metales como el cobre y el oro, mientras que el vidrio y el teflón son malos conductores. En cualquier material dieléctrico , los electrones permanecen unidos a sus respectivos átomos y el material se comporta como un aislante . La mayoría de los semiconductores tienen un nivel variable de conductividad que se encuentra entre los extremos de conducción y aislamiento. ^[136] Por otro lado, los metales tienen una estructura de banda electrónica que contiene bandas electrónicas parcialmente llenas. La presencia de tales bandas permite que los electrones en los metales se comporten como si fueran electrones libres o deslocalizados . Estos electrones no están asociados con átomos específicos, por lo que cuando se aplica un campo eléctrico, son libres de moverse como un gas (llamado gas de Fermi ) ^[137] a través del material de manera muy similar a los electrones libres.

Debido a las colisiones entre electrones y átomos, la velocidad de desplazamiento de los electrones en un conductor es del orden de milímetros por segundo. Sin embargo, la velocidad a la que un cambio de corriente en un punto del material provoca cambios en las corrientes en otras partes del material, la velocidad de propagación , es típicamente alrededor del 75% de la velocidad de la luz. ^[138] Esto ocurre porque las señales eléctricas se propagan como una onda, y la velocidad depende de la constante dieléctrica del material. ^[139]

Los metales son relativamente buenos conductores del calor, principalmente porque los electrones deslocalizados tienen libertad para transportar energía térmica entre átomos. Sin embargo, a diferencia de la conductividad eléctrica, la conductividad térmica de un metal es casi independiente de la temperatura. Esto se expresa matemáticamente mediante la ley de Wiedemann-Franz ^[137] , que establece que la relación entre la conductividad térmica y la conductividad eléctrica es proporcional a la temperatura. El desorden térmico en la red metálica aumenta la resistividad eléctrica del material, lo que produce una dependencia de la temperatura para la corriente eléctrica. ^[140]

Cuando se enfrían por debajo de un punto llamado temperatura crítica , los materiales pueden sufrir una transición de fase en la que pierden toda resistividad a la corriente eléctrica, en un proceso conocido como superconductividad . En la teoría BCS , los pares de electrones llamados pares de Cooper tienen su movimiento acoplado a la materia cercana a través de vibraciones reticulares llamadas fonones , evitando así las colisiones con átomos que normalmente crean resistencia eléctrica. ^[141] (Los pares de Cooper tienen un radio de aproximadamente 100 nm, por lo que pueden superponerse entre sí). ^[142] Sin embargo, el mecanismo por el cual operan los superconductores de temperatura más alta sigue siendo incierto.

Los electrones dentro de sólidos conductores, que son cuasipartículas en sí mismos, cuando están estrechamente confinados a temperaturas cercanas al cero absoluto , se comportan como si se hubieran dividido en otras tres cuasipartículas : espinones , orbitones y holones . ^{[143] [144]} Los primeros llevan el espín y el momento magnético, los siguientes llevan su ubicación orbital mientras que los últimos cargan eléctricamente.

Según la teoría de la relatividad especial de Einstein , a medida que la velocidad de un electrón se acerca a la velocidad de la luz , desde el punto de vista de un observador su masa relativista aumenta, lo que hace cada vez más difícil acelerarlo desde dentro del marco de referencia del observador. La velocidad de un electrón puede acercarse, pero nunca alcanzar, la velocidad de la luz en el vacío, c . Sin embargo, cuando los electrones relativistas, es decir, electrones que se mueven a una velocidad cercana a c , se inyectan en un medio dieléctrico como el agua, donde la velocidad local de la luz es significativamente menor que c , los electrones viajan temporalmente más rápido que la luz en el medio. A medida que interactúan con el medio, generan una luz tenue llamada radiación Cherenkov . ^[145]

Los efectos de la relatividad especial se basan en una cantidad conocida como factor de Lorentz , definida como donde v es la velocidad de la partícula. La energía cinética Ke de un electrón que se mueve con velocidad _v es :${\displaystyle \scriptstyle \gamma =1/{\sqrt {1-{v^{2}}/{c^{2}}}}}$

${\displaystyle \displaystyle K_{\mathrm {e} }=(\gamma -1)m_{\mathrm {e} }c^{2},}$

donde m _e es la masa del electrón. Por ejemplo, el acelerador lineal de Stanford puede acelerar un electrón a aproximadamente 51 GeV. ^[146] Dado que un electrón se comporta como una onda, a una velocidad dada tiene una longitud de onda de De Broglie característica . Esto viene dado por λ _e  =  h / p donde h es la constante de Planck y p es el momento. ^[60] Para el electrón de 51 GeV anterior, la longitud de onda es de aproximadamente2,4 × 10 ⁻¹⁷  m , lo suficientemente pequeño para explorar estructuras muy por debajo del tamaño de un núcleo atómico. ^[147]

La teoría del Big Bang es la teoría científica más aceptada para explicar las primeras etapas de la evolución del Universo. ^[149] Durante el primer milisegundo del Big Bang, las temperaturas eran superiores a los 10 mil millones  de kelvins y los fotones tenían energías medias superiores a un millón de electronvoltios . Estos fotones eran lo suficientemente energéticos como para poder reaccionar entre sí y formar pares de electrones y positrones. Del mismo modo, los pares positrón-electrón se aniquilaban entre sí y emitían fotones energéticos:

gamma
+
gamma
↔
mi⁺
+
mi⁻

Durante esta fase de la evolución del Universo se mantuvo un equilibrio entre electrones, positrones y fotones. Sin embargo, después de 15 segundos, la temperatura del Universo descendió por debajo del umbral en el que podía producirse la formación de electrones y positrones. La mayoría de los electrones y positrones supervivientes se aniquilaron entre sí, liberando radiación gamma que recalentó brevemente el Universo. ^[150]

Por razones que siguen siendo inciertas, durante el proceso de aniquilación hubo un exceso en el número de partículas sobre las antipartículas. Por lo tanto, sobrevivió aproximadamente un electrón por cada mil millones de pares electrón-positrón. Este exceso coincidió con el exceso de protones sobre antiprotones, en una condición conocida como asimetría bariónica , lo que resultó en una carga neta de cero para el universo. ^{[151] [152]} Los protones y neutrones supervivientes comenzaron a participar en reacciones entre sí, en el proceso conocido como nucleosíntesis , formando isótopos de hidrógeno y helio , con trazas de litio . Este proceso alcanzó su punto máximo después de unos cinco minutos. ^[153] Los neutrones sobrantes sufrieron una desintegración beta negativa con una vida media de unos mil segundos, liberando un protón y un electrón en el proceso.

norte
→
pag
+
mi⁻
+
no
_mi

Para el próximo300 000 –Durante 400.000  años , los electrones sobrantes permanecieron demasiado energéticos para unirse a los núcleos atómicos . ^[154] Lo que siguió fue un período conocido como recombinación , cuando se formaron átomos neutros y el universo en expansión se volvió transparente a la radiación. ^[155]

Aproximadamente un millón de años después del Big Bang, comenzó a formarse la primera generación de estrellas . ^[155] Dentro de una estrella, la nucleosíntesis estelar da como resultado la producción de positrones a partir de la fusión de núcleos atómicos. Estas partículas de antimateria se aniquilan inmediatamente con electrones, liberando rayos gamma. El resultado neto es una reducción constante en el número de electrones y un aumento correspondiente en el número de neutrones. Sin embargo, el proceso de evolución estelar puede dar como resultado la síntesis de isótopos radiactivos. Los isótopos seleccionados pueden sufrir posteriormente una desintegración beta negativa, emitiendo un electrón y un antineutrino desde el núcleo. ^[156] Un ejemplo es el isótopo cobalto-60 ( ⁶⁰ Co), que se desintegra para formar níquel-60 (⁶⁰
Ni
). ^[157]

Al final de su vida, una estrella con más de 20 masas solares puede sufrir un colapso gravitacional para formar un agujero negro . ^[158] Según la física clásica , estos objetos estelares masivos ejercen una atracción gravitatoria lo suficientemente fuerte como para evitar que cualquier cosa, incluso la radiación electromagnética , escape más allá del radio de Schwarzschild . Sin embargo, se cree que los efectos de la mecánica cuántica permiten potencialmente la emisión de radiación de Hawking a esta distancia. Se cree que los electrones (y positrones) se crean en el horizonte de sucesos de estos remanentes estelares .

Cuando se crea un par de partículas virtuales (como un electrón y un positrón) en las proximidades del horizonte de sucesos, la posición espacial aleatoria puede hacer que una de ellas aparezca en el exterior; este proceso se denomina efecto túnel cuántico . El potencial gravitatorio del agujero negro puede entonces suministrar la energía que transforma esta partícula virtual en una partícula real, lo que le permite irradiar hacia el espacio. ^[159] A cambio, el otro miembro del par recibe energía negativa, lo que resulta en una pérdida neta de masa-energía por parte del agujero negro. La tasa de radiación de Hawking aumenta con la disminución de la masa, lo que finalmente hace que el agujero negro se evapore hasta que, finalmente, explota. ^[160]

Los rayos cósmicos son partículas que viajan a través del espacio con altas energías. Los eventos de energía tan alta comoSe han registrado 3,0 × 10 ²⁰  eV . ^[161] Cuando estas partículas chocan con nucleones en la atmósfera terrestre , se genera una lluvia de partículas, incluidos piones . ^[162] Más de la mitad de la radiación cósmica observada desde la superficie de la Tierra consiste en muones . La partícula llamada muón es un leptón producido en la atmósfera superior por la desintegración de un pión.

π⁻
→
micras⁻
+
no
_micras

Un muón, a su vez, puede desintegrarse para formar un electrón o un positrón. ^[163]

micras⁻
→
mi⁻
+
no
_mi+
no
_micras

La observación remota de electrones requiere la detección de la energía que irradian. Por ejemplo, en entornos de alta energía como la corona de una estrella, los electrones libres forman un plasma que irradia energía debido a la radiación de frenado . El gas de electrones puede sufrir oscilaciones de plasma , que son ondas causadas por variaciones sincronizadas en la densidad de electrones, y estas producen emisiones de energía que pueden detectarse mediante el uso de radiotelescopios . ^[165]

La frecuencia de un fotón es proporcional a su energía. Cuando un electrón ligado pasa de un nivel de energía a otro en un átomo, absorbe o emite fotones a frecuencias características. Por ejemplo, cuando los átomos son irradiados por una fuente de amplio espectro, aparecen líneas oscuras distintivas en el espectro de la radiación transmitida en los lugares donde los electrones del átomo absorben la frecuencia correspondiente. Cada elemento o molécula muestra un conjunto característico de líneas espectrales, como la serie espectral del hidrógeno . Cuando se detectan, las mediciones espectroscópicas de la fuerza y ​​el ancho de estas líneas permiten determinar la composición y las propiedades físicas de una sustancia. ^{[166] [167]}

En condiciones de laboratorio, las interacciones de electrones individuales pueden observarse por medio de detectores de partículas , que permiten medir propiedades específicas como energía, espín y carga. ^[168] El desarrollo de la trampa de Paul y la trampa de Penning permite contener partículas cargadas dentro de una pequeña región durante largos períodos. Esto permite mediciones precisas de las propiedades de las partículas. Por ejemplo, en un caso se utilizó una trampa de Penning para contener un solo electrón durante un período de 10 meses. ^[169] El momento magnético del electrón se midió con una precisión de once dígitos, lo que, en 1980, era una precisión mayor que la de cualquier otra constante física. ^[170]

Las primeras imágenes de vídeo de la distribución de energía de un electrón fueron captadas por un equipo de la Universidad de Lund en Suecia en febrero de 2008. Los científicos utilizaron destellos de luz extremadamente cortos, llamados pulsos de attosegundos , que permitieron observar por primera vez el movimiento de un electrón. ^{[171] [172]}

La distribución de los electrones en los materiales sólidos se puede visualizar mediante espectroscopia de fotoemisión con resolución angular (ARPES). Esta técnica emplea el efecto fotoeléctrico para medir el espacio recíproco (una representación matemática de las estructuras periódicas que se utiliza para inferir la estructura original). La ARPES se puede utilizar para determinar la dirección, la velocidad y la dispersión de los electrones dentro del material. ^[173]

Los haces de electrones se utilizan en soldadura . ^[175] Permiten densidades de energía de hasta10 ⁷  W·cm ⁻² a través de un diámetro de foco estrecho de 0,1–1,3 mm y normalmente no requieren material de relleno. Esta técnica de soldadura debe realizarse en vacío para evitar que los electrones interactúen con el gas antes de llegar a su objetivo, y se puede utilizar para unir materiales conductores que de otro modo se considerarían inadecuados para la soldadura. ^{[176] [177]}

La litografía por haz de electrones (EBL) es un método de grabado de semiconductores a resoluciones inferiores a un micrómetro . ^[178] Esta técnica está limitada por los altos costes, el bajo rendimiento, la necesidad de operar el haz en el vacío y la tendencia de los electrones a dispersarse en los sólidos. El último problema limita la resolución a unos 10 nm. Por este motivo, la EBL se utiliza principalmente para la producción de pequeñas cantidades de circuitos integrados especializados . ^[179]

El procesamiento con haces de electrones se utiliza para irradiar materiales con el fin de cambiar sus propiedades físicas o esterilizar productos médicos y alimenticios. ^[180] Los haces de electrones fluidifican o casi funden vidrios sin un aumento significativo de la temperatura con una irradiación intensiva: por ejemplo, la radiación intensiva de electrones provoca una disminución de muchos órdenes de magnitud de la viscosidad y una disminución gradual de su energía de activación. ^[181]

Los aceleradores de partículas lineales generan haces de electrones para el tratamiento de tumores superficiales en radioterapia . La terapia con electrones puede tratar lesiones cutáneas como carcinomas de células basales porque un haz de electrones solo penetra hasta una profundidad limitada antes de ser absorbido, normalmente hasta 5 cm para energías de electrones en el rango de 5 a 20 MeV. Un haz de electrones se puede utilizar para complementar el tratamiento de áreas que han sido irradiadas con rayos X. ^{[182] [183]}

Los aceleradores de partículas utilizan campos eléctricos para impulsar electrones y sus antipartículas a altas energías. Estas partículas emiten radiación de sincrotrón cuando pasan a través de campos magnéticos. La dependencia de la intensidad de esta radiación con el espín polariza el haz de electrones, un proceso conocido como el efecto Sokolov-Ternov . ^[h] Los haces de electrones polarizados pueden ser útiles para varios experimentos. La radiación de sincrotrón también puede enfriar los haces de electrones para reducir la propagación del momento de las partículas. Los haces de electrones y positrones colisionan cuando las partículas se aceleran a las energías requeridas; los detectores de partículas observan las emisiones de energía resultantes, que la física de partículas estudia. ^[184]

La difracción de electrones de baja energía (LEED) es un método que consiste en bombardear un material cristalino con un haz colimado de electrones y luego observar los patrones de difracción resultantes para determinar la estructura del material. La energía requerida de los electrones suele estar en el rango de 20 a 200 eV. ^[185] La técnica de difracción de electrones de alta energía por reflexión (RHEED) utiliza la reflexión de un haz de electrones disparado en varios ángulos bajos para caracterizar la superficie de los materiales cristalinos. La energía del haz suele estar en el rango de 8 a 20 keV y el ángulo de incidencia es de 1 a 4°. ^{[186] [187]}

El microscopio electrónico dirige un haz de electrones enfocado hacia una muestra. Algunos electrones cambian sus propiedades, como la dirección del movimiento, el ángulo y la fase y energía relativas a medida que el haz interactúa con el material. Los microscopistas pueden registrar estos cambios en el haz de electrones para producir imágenes del material resueltas atómicamente. ^[188] En luz azul, los microscopios ópticos convencionales tienen una resolución limitada por difracción de aproximadamente 200 nm. ^[189] En comparación, los microscopios electrónicos están limitados por la longitud de onda de De Broglie del electrón. Esta longitud de onda, por ejemplo, es igual a 0,0037 nm para electrones acelerados a través de un potencial de 100.000 voltios . ^[190] El microscopio de transmisión con corrección de aberración electrónica es capaz de una resolución inferior a 0,05 nm, que es más que suficiente para resolver átomos individuales. ^[191] Esta capacidad hace que el microscopio electrónico sea un instrumento de laboratorio útil para la obtención de imágenes de alta resolución. Sin embargo, los microscopios electrónicos son instrumentos caros y costosos de mantener.

Existen dos tipos principales de microscopios electrónicos: de transmisión y de barrido . Los microscopios electrónicos de transmisión funcionan como retroproyectores , con un haz de electrones que pasa a través de una rebanada de material y luego se proyecta mediante lentes sobre una diapositiva fotográfica o un dispositivo acoplado a la carga . Los microscopios electrónicos de barrido rasterizan un haz de electrones finamente enfocado, como en un televisor, a través de la muestra estudiada para producir la imagen. Los aumentos varían de 100× a 1.000.000× o más para ambos tipos de microscopios. El microscopio de efecto túnel de barrido utiliza el efecto túnel cuántico de los electrones desde una punta de metal afilada hacia el material estudiado y puede producir imágenes con resolución atómica de su superficie. ^{[192] [193] [194]}

En el láser de electrones libres (FEL), un haz de electrones relativista pasa a través de un par de onduladores que contienen conjuntos de imanes dipolares cuyos campos apuntan en direcciones alternas. Los electrones emiten radiación de sincrotrón que interactúa coherentemente con los mismos electrones para amplificar fuertemente el campo de radiación en la frecuencia de resonancia . El FEL puede emitir una radiación electromagnética coherente de alto brillo con una amplia gama de frecuencias, desde microondas hasta rayos X suaves. Estos dispositivos se utilizan en la fabricación, la comunicación y en aplicaciones médicas, como la cirugía de tejidos blandos. ^[195]

Los electrones son importantes en los tubos de rayos catódicos , que se han utilizado ampliamente como dispositivos de visualización en instrumentos de laboratorio, monitores de ordenador y televisores . ^[196] En un tubo fotomultiplicador , cada fotón que golpea el fotocátodo inicia una avalancha de electrones que produce un pulso de corriente detectable. ^[197] Los tubos de vacío utilizan el flujo de electrones para manipular señales eléctricas y desempeñaron un papel fundamental en el desarrollo de la tecnología electrónica. Sin embargo, han sido reemplazados en gran medida por dispositivos de estado sólido como el transistor . ^[198]