Mojadura

Parte de una serie sobre
Mecánica clásica
${\displaystyle {\textbf {F}}={\frac {d\mathbf {p} }{dt}}}$ Segunda ley del movimiento
Historia Cronología Libros de texto
Sucursales Aplicado Celestial Continuo Dinámica Cinemática Cinética Estática Mecánica estadística
Fundamentos Aceleración Momento angular Pareja Principio de D'Alembert Energía cinético potencial Fuerza Marco de referencia Marco de referencia inercial Impulso Inercia  / Momento de inercia Masa Potencia mecánica Trabajo mecánico Momento Impulso Espacio Velocidad Tiempo Esfuerzo de torsión Velocidad Trabajo virtual
Formulaciones Leyes del movimiento de Newton Mecánica analítica Mecánica lagrangiana Mecánica hamiltoniana Mecánica de Routh Ecuación de Hamilton-Jacobi Ecuación de movimiento de Appell Mecánica de Koopman-von Neumann
Temas centrales Mojadura Desplazamiento Ecuaciones de movimiento Leyes del movimiento de Euler Fuerza ficticia Fricción Oscilador armónico Marco de referencia inercial  / no inercial Mecánica del movimiento de partículas planas Movimiento  ( lineal ) Ley de gravitación universal de Newton Leyes del movimiento de Newton Velocidad relativa Cuerpo rígido dinámica Ecuaciones de Euler Movimiento armónico simple Vibración
Rotación Movimiento circular Marco de referencia giratorio Fuerza centrípeta Fuerza centrífuga reactivo Fuerza de Coriolis Péndulo Velocidad tangencial Frecuencia rotacional Aceleración angular  / desplazamiento  / frecuencia  / velocidad
Científicos Kepler Galileo Huygens Newton Horrocas Halley Maupertuis Daniel Bernoulli Juan Bernoulli Euler de Alembert Claro Lagrange Laplace Poisson Hamilton Jacobi Cauchy Routh Liouville Appell Gibbs Koopman von Neumann
Physics portal  Category
v t e

En sistemas físicos , la amortiguación es la pérdida de energía de un sistema oscilante por disipación . ^{[1] [2]} La amortiguación es una influencia dentro o sobre un sistema oscilatorio que tiene el efecto de reducir o prevenir su oscilación. ^[3] Los ejemplos de amortiguación incluyen amortiguación viscosa en un fluido (ver arrastre viscoso ), fricción superficial , radiación , ^[1] resistencia en osciladores electrónicos y absorción y dispersión de luz en osciladores ópticos . La amortiguación que no se basa en la pérdida de energía puede ser importante en otros sistemas oscilantes como los que ocurren en sistemas biológicos y bicicletas ^[4] (p. ej. Suspensión (mecánica) ). La amortiguación no debe confundirse con la fricción , que es un tipo de fuerza disipativa que actúa sobre un sistema. La fricción puede causar o ser un factor de amortiguación.

El coeficiente de amortiguamiento es una medida adimensional que describe cómo decaen las oscilaciones en un sistema después de una perturbación. Muchos sistemas exhiben un comportamiento oscilatorio cuando son perturbados desde su posición de equilibrio estático . Una masa suspendida de un resorte, por ejemplo, podría, si se tira y se suelta, rebotar hacia arriba y hacia abajo. En cada rebote, el sistema tiende a regresar a su posición de equilibrio, pero la sobrepasa. A veces, las pérdidas (por ejemplo, por fricción) amortiguan el sistema y pueden hacer que las oscilaciones decaigan gradualmente en amplitud hacia cero o se atenúen . El coeficiente de amortiguamiento es una medida que describe qué tan rápido decaen las oscilaciones de un rebote al siguiente.

El coeficiente de amortiguamiento es un parámetro del sistema, denotado por ζ (" zeta "), que puede variar desde no amortiguado ( ζ = 0 ), subamortiguado ( ζ < 1 ), pasando por críticamente amortiguado ( ζ = 1 ) hasta sobreamortiguado ( ζ > 1 ).

El comportamiento de los sistemas oscilantes suele ser de interés en una amplia gama de disciplinas, entre las que se incluyen la ingeniería de control , la ingeniería química , la ingeniería mecánica , la ingeniería estructural y la ingeniería eléctrica . La cantidad física que oscila varía mucho y podría ser el balanceo de un edificio alto con el viento o la velocidad de un motor eléctrico , pero un enfoque normalizado o no dimensionalizado puede ser conveniente para describir aspectos comunes del comportamiento.

Dependiendo de la cantidad de amortiguación presente, un sistema exhibe diferentes comportamientos y velocidades oscilatorias.

• En el caso de que el sistema masa-resorte no tenga ninguna pérdida, la masa oscilaría indefinidamente y cada rebote tendría la misma altura que el anterior. Este caso hipotético se denomina no amortiguado .
• Si el sistema contenía pérdidas elevadas, por ejemplo, si el experimento de resorte-masa se realizó en un fluido viscoso , la masa podría regresar lentamente a su posición de reposo sin sobrepasar nunca la capacidad normal. Este caso se denomina sobreamortiguado .
• Por lo general, la masa tiende a sobrepasar su posición inicial y luego regresa, sobrepasándola nuevamente. Con cada sobrepaso, se disipa algo de energía en el sistema y las oscilaciones se reducen a cero. Este caso se denomina subamortiguación.
• Entre los casos de sobreamortiguamiento y subamortiguamiento, existe un cierto nivel de amortiguamiento en el que el sistema no sobrepasará el límite y no realizará ni una sola oscilación. Este caso se denomina amortiguamiento crítico . La diferencia clave entre el amortiguamiento crítico y el sobreamortiguamiento es que, en el amortiguamiento crítico, el sistema vuelve al equilibrio en el mínimo tiempo posible. ^[5]

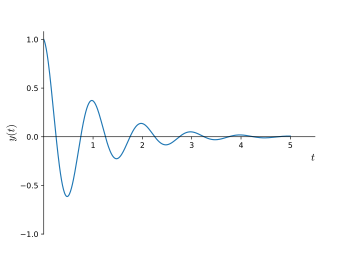
Una onda sinusoidal amortiguada o senoide amortiguada es una función sinusoidal cuya amplitud se acerca a cero a medida que aumenta el tiempo. Corresponde al caso subamortiguado de los sistemas de segundo orden amortiguados, o ecuaciones diferenciales de segundo orden subamortiguadas. ^[6] Las ondas sinusoidales amortiguadas se ven comúnmente en ciencia e ingeniería , dondequiera que un oscilador armónico esté perdiendo energía más rápido de lo que está siendo suministrada. Una onda sinusoidal verdadera que comienza en el tiempo = 0 comienza en el origen (amplitud = 0). Una onda coseno comienza en su valor máximo debido a su diferencia de fase con respecto a la onda sinusoidal. Una forma de onda sinusoidal dada puede ser de fase intermedia, teniendo componentes seno y coseno. El término "onda sinusoidal amortiguada" describe todas esas formas de onda amortiguadas, cualquiera sea su fase inicial.

La forma más común de amortiguamiento, que suele asumirse, es la que se encuentra en los sistemas lineales. Esta forma es el amortiguamiento exponencial, en el que la envolvente exterior de los picos sucesivos es una curva de decaimiento exponencial. Es decir, cuando se conecta el punto máximo de cada curva sucesiva, el resultado se asemeja a una función de decaimiento exponencial. La ecuación general para una sinusoide amortiguada exponencialmente puede representarse como: donde:$${\displaystyle y(t)=Ae^{-\lambda t}\cos(\omega t-\varphi )}$$

• ${\displaystyle y(t)}$es la amplitud instantánea en el tiempo t ;
• ${\displaystyle A}$es la amplitud inicial de la envolvente;
• ${\displaystyle \lambda }$es la tasa de decaimiento, en el recíproco de las unidades de tiempo de la variable independiente t ;
• ${\displaystyle \varphi }$es el ángulo de fase en t = 0 ;
• ${\displaystyle \omega }$es la frecuencia angular .

Otros parámetros importantes incluyen:

• Frecuencia : número de ciclos por unidad de tiempo. Se expresa en unidades de tiempo inversas o hercios .${\displaystyle f=\omega /(2\pi )}$${\displaystyle t^{-1}}$
• Constante de tiempo : , el tiempo que tarda la amplitud en disminuir por el factor e .${\displaystyle \tau =1/\lambda }$
• La vida media es el tiempo que tarda la envolvente de amplitud exponencial en disminuir en un factor de 2. Es igual a que es aproximadamente .${\displaystyle \ln(2)/\lambda }$${\displaystyle 0.693/\lambda }$
• Relación de amortiguamiento: es una caracterización adimensional de la tasa de desintegración en relación con la frecuencia, aproximadamente o exactamente .${\displaystyle \zeta }$${\displaystyle \zeta =\lambda /\omega }$${\displaystyle \zeta =\lambda /{\sqrt {\lambda ^{2}+\omega ^{2}}}<1}$
• Factor Q : es otra caracterización adimensional de la cantidad de amortiguación; un factor Q alto indica una amortiguación lenta en relación con la oscilación.${\displaystyle Q=1/(2\zeta )}$

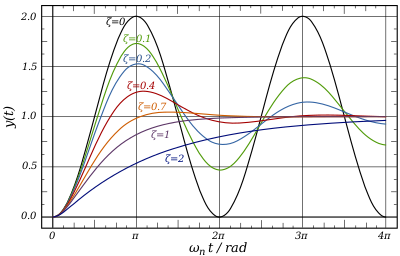
El coeficiente de amortiguamiento es un parámetro, usualmente denotado por ζ (letra griega zeta), ^[7] que caracteriza la respuesta de frecuencia de una ecuación diferencial ordinaria de segundo orden . Es particularmente importante en el estudio de la teoría de control . También es importante en el oscilador armónico . En general, los sistemas con coeficientes de amortiguamiento más altos (uno o más) demostrarán un mayor efecto de amortiguamiento. Los sistemas subamortiguados tienen un valor de menos de uno. Los sistemas críticamente amortiguados tienen un coeficiente de amortiguamiento de exactamente 1, o al menos muy cercano a él.

El coeficiente de amortiguamiento proporciona un medio matemático para expresar el nivel de amortiguamiento en un sistema en relación con el amortiguamiento crítico. Para un oscilador armónico amortiguado con masa m , coeficiente de amortiguamiento c y constante de resorte k , se puede definir como la relación entre el coeficiente de amortiguamiento en la ecuación diferencial del sistema y el coeficiente de amortiguamiento crítico:

${\displaystyle \zeta ={\frac {c}{c_{c}}}={\frac {\text{actual damping}}{\text{critical damping}}},}$

donde la ecuación de movimiento del sistema es

${\displaystyle m{\frac {d^{2}x}{dt^{2}}}+c{\frac {dx}{dt}}+kx=0}$. ^[8]

y el coeficiente de amortiguamiento crítico correspondiente es

${\displaystyle c_{c}=2{\sqrt {km}}}$

o

${\displaystyle c_{c}=2m{\sqrt {\frac {k}{m}}}=2m\omega _{n}}$

dónde

${\displaystyle \omega _{n}={\sqrt {\frac {k}{m}}}}$es la frecuencia natural del sistema.

El coeficiente de amortiguamiento es adimensional, siendo el cociente de dos coeficientes de unidades idénticas.

Usando la frecuencia natural de un oscilador armónico y la definición de la relación de amortiguamiento anterior, podemos reescribir esto como:${\textstyle \omega _{n}={\sqrt {{k}/{m}}}}$

${\displaystyle {\frac {d^{2}x}{dt^{2}}}+2\zeta \omega _{n}{\frac {dx}{dt}}+\omega _{n}^{2}x=0.}$

Esta ecuación es más general que el sistema masa-resorte y también se aplica a circuitos eléctricos y a otros dominios. Se puede resolver con el enfoque

${\displaystyle x(t)=Ce^{st},}$

donde C y s son ambas constantes complejas , y s satisface

${\displaystyle s=-\omega _{n}\left(\zeta \pm i{\sqrt {1-\zeta ^{2}}}\right).}$

Dos de estas soluciones, para los dos valores de s que satisfacen la ecuación, se pueden combinar para formar las soluciones reales generales, con propiedades oscilatorias y decrecientes en varios regímenes:

Sin amortiguar

Es el caso donde corresponde al oscilador armónico simple no amortiguado, y en ese caso la solución parece ser , como se esperaba. Este caso es extremadamente raro en el mundo natural y los ejemplos más cercanos son casos en los que la fricción se redujo deliberadamente a valores mínimos.${\displaystyle \zeta =0}$${\displaystyle \exp(i\omega _{n}t)}$

Amortiguación insuficiente

Si s es un par de valores complejos, entonces cada término de solución compleja es una exponencial decreciente combinada con una porción oscilatoria que se parece a . Este caso ocurre para , y se lo conoce como subamortiguado (por ejemplo, cable elástico).${\textstyle \exp \left(i\omega _{n}{\sqrt {1-\zeta ^{2}}}t\right)}$${\displaystyle \ 0\leq \zeta <1}$

Sobreamortiguado

Si s es un par de valores reales, entonces la solución es simplemente una suma de dos exponenciales decrecientes sin oscilación. Este caso ocurre para , y se conoce como sobreamortiguado . Las situaciones en las que la sobreamortiguación es práctica tienden a tener resultados trágicos si se produce un exceso, generalmente eléctrico en lugar de mecánico. Por ejemplo, aterrizar un avión con piloto automático: si el sistema se excede y suelta el tren de aterrizaje demasiado tarde, el resultado sería un desastre.${\displaystyle \zeta >1}$

Críticamente amortiguado

El caso en el que se encuentra en el límite entre los casos sobreamortiguado y subamortiguado, se denomina críticamente amortiguado . Esto resulta ser un resultado deseable en muchos casos en los que se requiere el diseño de ingeniería de un oscilador amortiguado (por ejemplo, un mecanismo de cierre de puertas).${\displaystyle \zeta =1}$

El factor Q , la relación de amortiguamiento ζ y la tasa de decaimiento exponencial α están relacionados de tal manera que ^[9]

${\displaystyle \zeta ={\frac {1}{2Q}}={\alpha \over \omega _{n}}.}$

Cuando un sistema de segundo orden tiene (es decir, cuando el sistema está subamortiguado), tiene dos polos conjugados complejos que tienen cada uno una parte real de ; es decir, el parámetro de tasa de decaimiento representa la tasa de decaimiento exponencial de las oscilaciones. Una relación de amortiguamiento menor implica una tasa de decaimiento menor, y por eso los sistemas muy subamortiguados oscilan durante tiempos largos. ^[10] Por ejemplo, un diapasón de alta calidad , que tiene una relación de amortiguamiento muy baja, tiene una oscilación que dura mucho tiempo, decayendo muy lentamente después de ser golpeado por un martillo.${\displaystyle \zeta <1}$${\displaystyle -\alpha }$${\displaystyle \alpha }$

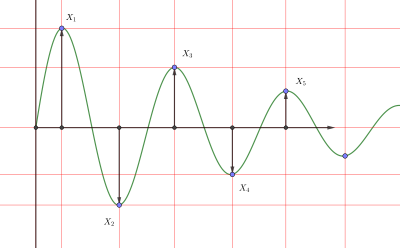
En el caso de vibraciones subamortiguadas, el coeficiente de amortiguamiento también está relacionado con el decremento logarítmico . El coeficiente de amortiguamiento se puede encontrar para dos picos cualesquiera, incluso si no son adyacentes. ^[11] Para picos adyacentes: ^[12]${\displaystyle \delta }$

${\displaystyle \zeta ={\frac {\delta }{\sqrt {\delta ^{2}+\left(2\pi \right)^{2}}}}}$ dónde${\displaystyle \delta =\ln {\frac {x_{0}}{x_{1}}}}$

donde x ₀ y x ₁ son amplitudes de dos picos sucesivos.

Como se muestra en la figura de la derecha:

${\displaystyle \delta =\ln {\frac {x_{1}}{x_{3}}}=\ln {\frac {x_{2}}{x_{4}}}=\ln {\frac {x_{1}-x_{2}}{x_{3}-x_{4}}}}$

donde , son amplitudes de dos picos positivos sucesivos y , son amplitudes de dos picos negativos sucesivos.${\displaystyle x_{1}}$${\displaystyle x_{3}}$${\displaystyle x_{2}}$${\displaystyle x_{4}}$

En la teoría de control , el sobreimpulso se refiere a una salida que excede su valor final en estado estable. ^[13] Para una entrada escalonada , el sobreimpulso porcentual (PO) es el valor máximo menos el valor del escalón dividido por el valor del escalón. En el caso del escalón unitario, el sobreimpulso es simplemente el valor máximo de la respuesta al escalón menos uno.

El porcentaje de sobreimpulso (PO) está relacionado con el coeficiente de amortiguamiento ( ζ ) por:

${\displaystyle \mathrm {PO} =100\exp \left({-{\frac {\zeta \pi }{\sqrt {1-\zeta ^{2}}}}}\right)}$

Por el contrario, el coeficiente de amortiguamiento ( ζ ) que produce un sobreimpulso porcentual dado viene dado por:

${\displaystyle \zeta ={\frac {-\ln \left({\frac {\rm {PO}}{100}}\right)}{\sqrt {\pi ^{2}+\ln ^{2}\left({\frac {\rm {PO}}{100}}\right)}}}}$

Cuando un objeto cae por el aire, la única fuerza que se opone a su caída libre es la resistencia del aire. Un objeto que cae a través del agua o del aceite se desaceleraría a un ritmo mayor, hasta que finalmente alcanzaría una velocidad de estado estable a medida que la fuerza de arrastre se equilibra con la fuerza de la gravedad. Este es el concepto de arrastre viscoso , que, por ejemplo, se aplica en puertas automáticas o puertas antigolpes. ^[14]

Los sistemas eléctricos que funcionan con corriente alterna (CA) utilizan resistencias para amortiguar los circuitos resonantes LC. ^[14]

La energía cinética que provoca las oscilaciones se disipa en forma de calor mediante corrientes de Foucault eléctricas que se inducen al pasar a través de los polos de un imán, ya sea por una bobina o una placa de aluminio. Las corrientes de Foucault son un componente clave de la inducción electromagnética , ya que establecen un flujo magnético que se opone directamente al movimiento oscilatorio, creando una fuerza resistiva. ^[15] En otras palabras, la resistencia causada por las fuerzas magnéticas ralentiza un sistema. Un ejemplo de la aplicación de este concepto son los frenos de las montañas rusas. ^[16]

Los amortiguadores magnetorreológicos (amortiguadores MR) utilizan fluido magnetorreológico , que cambia de viscosidad cuando se somete a un campo magnético. En este caso, la amortiguación magnetorreológica puede considerarse una forma interdisciplinaria de amortiguación con mecanismos de amortiguación tanto viscosos como magnéticos. ^{[17] [18]}

• "Amortiguación". Enciclopedia Británica .
• OpenStax, Universidad. "Física". Lumen .