Dibujo de curvas

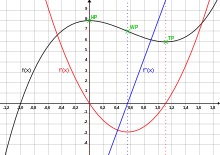
En geometría , el trazado de curvas (o dibujo de curvas ) es una técnica que permite obtener una idea aproximada de la forma general de una curva plana a partir de su ecuación, sin tener que calcular la gran cantidad de puntos necesarios para obtener un gráfico detallado. Se trata de una aplicación de la teoría de curvas para encontrar sus características principales.

Las siguientes operaciones suelen ser fáciles de realizar y proporcionan pistas importantes sobre la forma de una curva:

• Determinar los puntos de corte en x e y de la curva. Los puntos de corte en x se encuentran igualando y a 0 en la ecuación de la curva y despejando x . De manera similar, los puntos de corte en y se encuentran igualando x a 0 en la ecuación de la curva y despejando y .
• Determinar la simetría de la curva. Si el exponente de x es siempre par en la ecuación de la curva, entonces el eje y es un eje de simetría para la curva. De manera similar, si el exponente de y es siempre par en la ecuación de la curva, entonces el eje x es un eje de simetría para la curva. Si la suma de los grados de x e y en cada término es siempre par o siempre impar, entonces la curva es simétrica respecto del origen y el origen se denomina centro de la curva.
• Determinar los límites de los valores de x e y .
• Si la curva pasa por el origen, determine las líneas tangentes allí. Para las curvas algebraicas, esto se puede hacer eliminando todos los términos de la ecuación, excepto los de orden más bajo, y resolviéndolos.
• De manera similar, al eliminar todos los términos excepto los de orden más alto de la ecuación y resolverlos, se obtienen los puntos donde la curva se encuentra con la línea en el infinito .
• Determinar las asíntotas de la curva. Determinar también desde qué lado la curva se aproxima a las asíntotas y dónde las asíntotas intersecan la curva. ^[1]
• Igualar la primera y la segunda derivadas a 0 para encontrar los puntos estacionarios y los puntos de inflexión respectivamente. Si la ecuación de la curva no se puede resolver explícitamente para x o y , para encontrar estas derivadas se requiere una diferenciación implícita .

El diagrama de Newton (también conocido como paralelogramo de Newton , en honor a Isaac Newton ) es una técnica para determinar la forma de una curva algebraica cerca y lejos del origen. Consiste en representar gráficamente (α, β) para cada término Ax ^α y ^β en la ecuación de la curva. El diagrama resultante se analiza a continuación para obtener información sobre la curva.

En concreto, dibuje una línea diagonal que conecte dos puntos en el diagrama de modo que todos los demás puntos estén sobre o a la derecha y por encima de ella. Hay al menos una de esas líneas si la curva pasa por el origen. Sea la ecuación de la línea q α+ p β= r . Suponga que la curva se aproxima mediante y = Cx ^p/q cerca del origen. Entonces el término Ax ^α y ^β es aproximadamente Dx ^α+βp/q . El exponente es r/q cuando (α, β) está sobre la línea y mayor cuando está por encima y a la derecha. Por lo tanto, los términos significativos cerca del origen bajo este supuesto son solo los que se encuentran sobre la línea y los demás pueden ignorarse; produce una ecuación aproximada simple para la curva. Puede haber varias líneas diagonales de este tipo, cada una correspondiente a una o más ramas de la curva, y las ecuaciones aproximadas de las ramas pueden encontrarse aplicando este método a cada línea por turno.

Por ejemplo, el folio de Descartes se define mediante la ecuación

${\displaystyle x^{3}+y^{3}-3axy=0\,}$.

Entonces el diagrama de Newton tiene puntos en (3, 0), (1, 1) y (0, 3). Se pueden trazar dos líneas diagonales como se describió anteriormente, 2α+β=3 y α+2β=3. Estas producen

${\displaystyle x^{2}-3ay=0\,}$

${\displaystyle y^{2}-3ax=0\,}$

como ecuaciones aproximadas para las ramas horizontales y verticales de la curva donde se cruzan en el origen. ^[2]

De Gua extendió el diagrama de Newton para formar una técnica llamada triángulo analítico (o triángulo de De Gua ). Los puntos (α, β) se trazan como con el método del diagrama de Newton, pero se agrega la línea α+β= n , donde n es el grado de la curva, para formar un triángulo que contiene el diagrama. Este método considera todas las líneas que delimitan el polígono convexo más pequeño que contiene los puntos trazados (ver envoltura convexa ). ^[3]

• Rastreo de líneas optimizadas en dinámica de fluidos

• Curva
• Lugar
• Curva algebraica
• Función padre
• Continuación numérica
• Cubos de marcha
• Trazado de límites
• Tira triangular

• Trenogin, VA (2001) [1994], "Diagrama de Newton", Enciclopedia de Matemáticas , EMS Press