Ángulo de visión (fotografía)

En fotografía , el ángulo de visión ( AOV ) ^[1] describe la extensión angular de una escena dada captada por una cámara . Se utiliza indistintamente con el término más general campo de visión .

Es importante distinguir el ángulo de visión del ángulo de cobertura , que describe el rango de ángulos que una lente puede captar. Normalmente, el círculo de imagen producido por una lente es lo suficientemente grande como para cubrir la película o el sensor por completo, posiblemente incluyendo algo de viñeteado hacia el borde. Si el ángulo de cobertura de la lente no llena el sensor, el círculo de imagen será visible, normalmente con un fuerte viñeteado hacia el borde, y el ángulo de visión efectivo estará limitado al ángulo de cobertura.

El ángulo de visión de una cámara no depende solo del objetivo, sino también del sensor. Los sensores digitales suelen ser más pequeños que la película de 35 mm , y esto hace que el objetivo tenga un ángulo de visión más estrecho que con la película de 35 mm, por un factor constante para cada sensor (llamado factor de recorte ). En las cámaras digitales de uso diario, el factor de recorte puede variar de alrededor de 1 ( SLR digitales profesionales ), a 1,6 (SLR de consumo), a 2 ( Micro Four Thirds ILC) a 6 (la mayoría de las cámaras compactas ). Por lo tanto, un objetivo estándar de 50 mm para fotografía de 35 mm actúa como un objetivo de "película" estándar de 50 mm en una SLR digital profesional, pero actuaría más cerca de un objetivo de 80 mm (1,6×50 mm) en muchas DSLR de mercado medio, y el ángulo de visión de 40 grados de un objetivo estándar de 50 mm en una cámara de película es equivalente a un objetivo de 80 mm en muchas SLR digitales.

Para lentes que proyectan imágenes rectilíneas (no distorsionadas espacialmente) de objetos distantes, la longitud focal efectiva y las dimensiones del formato de imagen definen completamente el ángulo de visión. Los cálculos para lentes que producen imágenes no rectilíneas son mucho más complejos y, al final, no muy útiles en la mayoría de las aplicaciones prácticas. (En el caso de una lente con distorsión, por ejemplo, una lente ojo de pez , una lente más larga con distorsión puede tener un ángulo de visión más amplio que una lente más corta con baja distorsión) ^[3] El ángulo de visión se puede medir horizontalmente (desde el borde izquierdo al derecho del marco), verticalmente (desde la parte superior a la inferior del marco) o diagonalmente (desde una esquina del marco a su esquina opuesta).

Para una lente que proyecta una imagen rectilínea (enfocada al infinito, ver derivación), el ángulo de visión ( α ) se puede calcular a partir de la dimensión elegida ( d ) y la distancia focal efectiva ( f ) de la siguiente manera: ^[4]$${\displaystyle \alpha =2\arctan {\frac {d}{2f}}}$$

${\estilo de visualización d}$representa el tamaño de la película (o sensor) en la dirección medida (ver más abajo: efectos del sensor) . Por ejemplo, para una película de 35 mm que tiene 36 mm de ancho y 24 mm de alto, se utilizaría para obtener el ángulo de visión horizontal y para el ángulo vertical.${\displaystyle d=36\,\mathrm {mm} }$${\displaystyle d=24\,\mathrm {mm} }$

Como se trata de una función trigonométrica, el ángulo de visión no varía de forma lineal con el recíproco de la distancia focal. Sin embargo, excepto en el caso de los objetivos gran angular, es razonable aproximarse en radianes o grados.${\displaystyle \alpha \approx {\frac {d}{f}}}$${\displaystyle {\frac {180d}{\pi f}}}$

La distancia focal efectiva es casi igual a la distancia focal indicada del objetivo ( F ), excepto en la fotografía macro , donde la distancia del objetivo al objeto es comparable a la distancia focal. En este caso, se debe tener en cuenta el factor de aumento ( m ):$${\displaystyle f=F\cdot(1+m)}$$

(En fotografía se suele definir como positiva, a pesar de la imagen invertida.) Por ejemplo, con una relación de aumento de 1:2, encontramos y con ello el ángulo de visión se reduce en un 33% respecto a enfocar un objeto lejano con la misma lente.${\estilo de visualización m}$${\displaystyle f=1.5\cdot F}$

El ángulo de visión también se puede determinar utilizando tablas de campo de visión o calculadoras de lentes en papel o software. ^[5]

Gráficos logarítmicos de distancia focal frente a factor de recorte frente a ángulos de visión diagonales, horizontales y verticales para película o sensores con relaciones de aspecto de 3:2 y 4:3. La línea amarilla muestra un ejemplo en el que 18 mm en formato APS-C 3:2 equivale a 27 mm y produce un ángulo vertical de 48 grados.

Considere una cámara de 35 mm con una lente que tiene una distancia focal de F = 50 mm . Las dimensiones del formato de imagen de 35 mm son 24 mm (verticalmente) × 36 mm (horizontalmente), lo que da una diagonal de aproximadamente 43,3 mm.

En el foco infinito, f = F , los ángulos de visión son:

• horizontalmente,${\displaystyle \alpha _{h}=2\arctan {\frac {h}{2f}}=2\arctan {\frac {36}{2\times 50}}\aproximadamente 39,6^{\circ }}$
• verticalmente,${\displaystyle \alpha _{v}=2\arctan {\frac {v}{2f}}=2\arctan {\frac {24}{2\times 50}}\aproximadamente 27,0^{\circ }}$
• diagonalmente,${\displaystyle \alpha _{d}=2\arctan {\frac {d}{2f}}=2\arctan {\frac {43,3}{2\times 50}}\aproximadamente 46,8^{\circ }}$

Consideremos una lente rectilínea en una cámara utilizada para fotografiar un objeto a una distancia , y que forma una imagen que apenas cabe en la dimensión, , del marco (la película o el sensor de imagen ). Tratemos la lente como si fuera un agujero de alfiler a una distancia del plano de la imagen (técnicamente, el centro de perspectiva de una lente rectilínea está en el centro de su pupila de entrada ): ^[6]$Estilo de visualización S_{1}$${\estilo de visualización d}$$Estilo de visualización S_{2}$

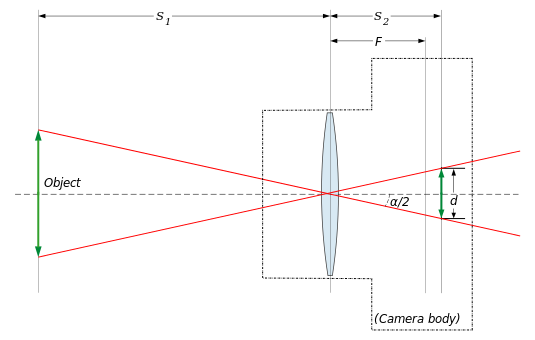
Ahora bien, es el ángulo que forma el eje óptico de la lente y el rayo que une su centro óptico con el borde de la película. Aquí se define como el ángulo de visión, ya que es el ángulo que encierra el objeto más grande cuya imagen puede caber en la película. Queremos encontrar la relación entre:${\displaystyle \alpha /2}$${\estilo de visualización \alpha}$

• El ángulo${\estilo de visualización \alpha}$
• el lado "opuesto" del triángulo rectángulo (la mitad de la dimensión del formato de película)${\estilo de visualización d/2}$
• el lado "adyacente", (distancia desde la lente hasta el plano de la imagen)$Estilo de visualización S_{2}$

Usando trigonometría básica, encontramos: que podemos resolver para α , dando:$${\displaystyle \tan(\alpha /2)={\frac {d/2}{S_{2}}}.}$$$${\displaystyle \alpha =2\arctan {\frac {d}{2S_{2}}}}$$

Para proyectar una imagen nítida de objetos distantes, se necesita una distancia focal igual a , que se logra configurando la lente para enfocar al infinito . Entonces, el ángulo de visión viene dado por:$Estilo de visualización S_{2}$${\estilo de visualización F}$

$${\displaystyle \alpha =2\arctan {\frac {d}{2f}}}$$dónde .${\displaystyle f=F}$

Nótese que el ángulo de visión varía ligeramente cuando el foco no está en el infinito (ver respiración (lente) ), lo que se obtiene reorganizando la ecuación de la lente.${\displaystyle S_{2}={\frac {S_{1}f}{S_{1}-f}}}$

Para la fotografía macro, no podemos descuidar la diferencia entre y . De la fórmula de lente fina ,$Estilo de visualización S_{2}$${\estilo de visualización F}$$${\displaystyle {\frac {1}{F}}={\frac {1}{S_{1}}}+{\frac {1}{S_{2}}}.}$$

A partir de la definición de aumento , , podemos sustituir y con algo de álgebra encontrar:${\displaystyle m=S_{2}/S_{1}}$$Estilo de visualización S_{1}$$${\displaystyle S_{2}=F\cdot (1+m)}$$

Definiendo como la “distancia focal efectiva”, obtenemos la fórmula presentada anteriormente: donde .$estilo de visualización f=S_{2}}$$${\displaystyle \alpha =2\arctan {\frac {d}{2f}}}$$${\displaystyle f=F\cdot(1+m)}$

Un segundo efecto que entra en juego en la fotografía macro es la asimetría de la lente (una lente asimétrica es una lente en la que la apertura parece tener dimensiones diferentes cuando se ve desde el frente y desde atrás). La asimetría de la lente causa un desfase entre el plano nodal y las posiciones de la pupila. El efecto se puede cuantificar utilizando la relación ( P ) entre el diámetro aparente de la pupila de salida y el diámetro de la pupila de entrada. La fórmula completa para el ángulo de visión ahora se convierte en: ^[7]$${\displaystyle \alpha =2\arctan {\frac {d}{2F\cdot (1+m/P)}}}$$

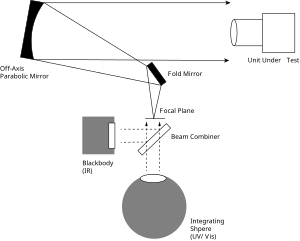
En la industria de instrumentación óptica, el término campo de visión (FOV) es el más utilizado, aunque las mediciones todavía se expresan como ángulos. ^[8] Las pruebas ópticas se utilizan comúnmente para medir el campo de visión de sensores y cámaras UV , visibles e infrarrojos (longitudes de onda de aproximadamente 0,1 a 20 μm en el espectro electromagnético ).

El objetivo de esta prueba es medir el campo de visión horizontal y vertical de una lente y un sensor utilizados en un sistema de imágenes, cuando no se conoce la longitud focal de la lente o el tamaño del sensor (es decir, cuando el cálculo anterior no es inmediatamente aplicable). Aunque este es un método típico que utiliza la industria óptica para medir el campo de visión, existen muchos otros métodos posibles.

La luz ultravioleta/visible de una esfera integradora (y/u otra fuente como un cuerpo negro ) se enfoca sobre un objetivo de prueba cuadrado en el plano focal de un colimador (los espejos en el diagrama), de modo que la cámara que se está probando verá una imagen virtual del objetivo de prueba a una distancia infinita. La cámara que se está probando detecta una imagen real de la imagen virtual del objetivo y la imagen detectada se muestra en un monitor. ^[9]

La imagen captada, que incluye el objetivo, se muestra en un monitor, donde se puede medir. Las dimensiones de la imagen completa y de la parte de la imagen que es el objetivo se determinan mediante inspección (las medidas se expresan normalmente en píxeles, pero también pueden expresarse en pulgadas o centímetros).

• ${\displaystyle D}$= dimensión de la imagen completa
• ${\displaystyle d}$= dimensión de la imagen del objetivo

La imagen virtual distante del objetivo que genera el colimador subtiende un cierto ángulo, denominado extensión angular del objetivo, que depende de la longitud focal del colimador y del tamaño del objetivo. Suponiendo que la imagen detectada incluye todo el objetivo, el ángulo que ve la cámara, su campo de visión, es esta extensión angular del objetivo multiplicada por la relación entre el tamaño de la imagen completa y el tamaño de la imagen del objetivo. ^[10]

La extensión angular del objetivo es: donde es la dimensión del objetivo y es la distancia focal del colimador.$${\displaystyle \alpha =2\arctan {\frac {L}{2f_{c}}}}$$${\displaystyle L}$${\displaystyle f_{c}}$

El campo de visión total es entonces aproximadamente: o más precisamente, si el sistema de imágenes es rectilíneo :$${\displaystyle \mathrm {FOV} =\alpha {\frac {D}{d}}}$$$${\displaystyle \mathrm {FOV} =2\arctan {\frac {LD}{2f_{c}d}}}$$

Este cálculo podría ser un campo de visión horizontal o vertical, dependiendo de cómo se midan el objetivo y la imagen.

A menudo se hace referencia a las lentes mediante términos que expresan su ángulo de visión:

• Objetivos ojo de pez : las distancias focales típicas son de entre 8 mm y 10 mm para imágenes circulares y de entre 15 y 16 mm para imágenes de fotograma completo. Hasta 180° y más.
  • Un objetivo ojo de pez circular (a diferencia de un ojo de pez de fotograma completo) es un ejemplo de objetivo en el que el ángulo de cobertura es menor que el ángulo de visión. La imagen proyectada sobre la película es circular porque el diámetro de la imagen proyectada es más estrecho que el necesario para cubrir la parte más ancha de la película.
• Un objetivo ultra gran angular es un objetivo rectilíneo que tiene una longitud focal inferior a 24 mm en un formato de película de 35 mm, aquí 14 mm da 114° y 24 mm da 84°.
• Los objetivos gran angular (24–35 mm en formato de película de 35 mm) cubren entre 84° y 64°
• Las lentes normales o estándar (36–60 mm en formato de película de 35 mm) cubren entre 62° y 40°
• Los objetivos de enfoque largo (cualquier objetivo con una distancia focal mayor que la diagonal de la película o el sensor utilizado) ^[11] generalmente tienen un ángulo de visión de 35° o menos. ^[12] Dado que los fotógrafos generalmente solo se encuentran con el subtipo de objetivo telefoto , ^[13] se los conoce en el lenguaje fotográfico común como:
• "Telefoto medio", una distancia focal de 85 mm a 250 mm en formato de película de 35 mm que cubre entre 30° y 10° ^[14]
• Los "superteleobjetivos" (más de 300 mm en formato de película de 35 mm) generalmente cubren entre 8° y menos de 1° ^[14]

Los lentes con zoom son un caso especial en el que la distancia focal y, por lo tanto, el ángulo de visión del lente se pueden alterar mecánicamente sin quitar el lente de la cámara.

Para una distancia dada entre la cámara y el objeto, los lentes más largos amplían más el objeto. Para un aumento dado del objeto (y, por lo tanto, para diferentes distancias entre la cámara y el objeto), los lentes más largos parecen comprimir la distancia; los lentes más anchos parecen expandir la distancia entre los objetos.

Otro resultado de utilizar un objetivo gran angular es una mayor distorsión aparente de la perspectiva cuando la cámara no está alineada perpendicularmente al sujeto: las líneas paralelas convergen a la misma velocidad que con un objetivo normal , pero convergen más debido al campo total más amplio. Por ejemplo, los edificios parecen caer hacia atrás mucho más abruptamente cuando la cámara apunta hacia arriba desde el nivel del suelo que si se fotografiaran con un objetivo normal a la misma distancia del sujeto, porque se ve más del edificio del sujeto en la toma gran angular.

Debido a que diferentes lentes generalmente requieren una distancia diferente entre la cámara y el sujeto para preservar el tamaño del sujeto, cambiar el ángulo de visión puede distorsionar indirectamente la perspectiva, cambiando el tamaño relativo aparente del sujeto y el primer plano.

Si el tamaño de la imagen del sujeto permanece igual, entonces, en cualquier apertura dada, todos los lentes, gran angular y lentes largos, darán la misma profundidad de campo . ^[15]

Un ejemplo de cómo la elección de la lente afecta el ángulo de visión.

Esta tabla muestra los ángulos de visión diagonal, horizontal y vertical, en grados, para lentes que producen imágenes rectilíneas, cuando se utilizan con formato de 36 mm × 24 mm (es decir, película de 135 o fotograma completo digital de 35 mm usando ancho de 36 mm, alto de 24 mm y diagonal de 43,3 mm para d en la fórmula anterior). ^[16] Las cámaras compactas digitales a veces indican las distancias focales de sus lentes en equivalentes de 35 mm, que se pueden usar en esta tabla.

A modo de comparación, el sistema visual humano percibe un ángulo de visión de aproximadamente 140° por 80°. ^[17]

Cinco imágenes que utilizan longitudes de zoom equivalentes de 24, 28, 35, 50 y 72 mm, en formato vertical, para ilustrar los ángulos de visión ^[18]

Cinco imágenes que utilizan la función de zoom de pasos equivalentes de 24, 28, 35, 50 y 72 mm para ilustrar los ángulos de visión

Como se ha indicado anteriormente, el ángulo de visión de una cámara no depende solo del objetivo, sino también del sensor utilizado. Los sensores digitales suelen ser más pequeños que una película de 35 mm, lo que hace que el objetivo se comporte normalmente como lo haría un objetivo de mayor distancia focal y tenga un ángulo de visión más estrecho que con una película de 35 mm, en un factor constante para cada sensor (llamado factor de recorte ). En las cámaras digitales de uso diario, el factor de recorte puede oscilar entre aproximadamente 1 ( réflex digitales profesionales ) y 1,6 (réflex de gama media), hasta aproximadamente 3 o 6 en el caso de las cámaras compactas . Por lo tanto, un objetivo estándar de 50 mm para fotografía de 35 mm actúa como un objetivo de "película" estándar de 50 mm incluso en una SLR digital profesional, pero actuaría más cerca de un objetivo de 75 mm (1,5×50 mm Nikon) o de 80 mm (1,6×50 mm Canon) en muchas DSLR de mercado medio, y el ángulo de visión de 40 grados de un objetivo estándar de 50 mm en una cámara de película es equivalente a un objetivo de 28-35 mm en muchas SLR digitales.

La siguiente tabla muestra los ángulos de visión horizontal, vertical y diagonal, en grados, cuando se utiliza con un formato de 22,2 mm × 14,8 mm (que es el tamaño de cuadro APS-C de la DSLR de Canon ) y una diagonal de 26,7 mm.

La modificación del ángulo de visión a lo largo del tiempo (conocido como zoom ) es una técnica cinematográfica de uso frecuente , a menudo combinada con el movimiento de la cámara para producir un efecto de " dolly zoom ", que se hizo famoso gracias a la película Vértigo . El uso de un ángulo de visión amplio puede exagerar la velocidad percibida de la cámara y es una técnica común en los planos de seguimiento , los viajes fantasma y los videojuegos de carreras . Véase también Campo de visión en los videojuegos .

• Explicación sencilla del ángulo de visión y la distancia focal
• Ángulo de visión en cámaras SLR digitales con sensor de tamaño reducido
• Distancia focal y ángulo de visión