Punto de contacto cuántico

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Contacto puntual cuántico» – noticias  · periódicos  · libros  · académico  · JSTOR ( mayo de 2021 ) ( Aprenda cómo y cuándo eliminar este mensaje )

Un punto de contacto cuántico ( QPC ) es una estrecha constricción entre dos amplias regiones conductoras de electricidad , de un ancho comparable a la longitud de onda electrónica (nano a micrómetro). ^[1]

La importancia de los QPC radica en que demuestran la cuantificación de la conductancia balística en sistemas mesoscópicos. La conductancia de un QPC se cuantifica en unidades de , el llamado quantum de conductancia .$Estilo de visualización 2e^{2}/h$

Los contactos puntuales cuánticos fueron informados por primera vez en 1988 por un equipo holandés de la Universidad Tecnológica de Delft y Philips Research ^[2] y, de forma independiente, por un equipo británico del Laboratorio Cavendish . ^[3] Se basan en trabajos anteriores del grupo británico que mostraron cómo se podían usar puertas divididas para convertir un gas de electrones bidimensional en unidimensional, primero en silicio ^[4] y luego en arseniuro de galio . ^{[5] [6]}

Esta cuantificación recuerda a la cuantificación de la conductancia Hall , pero se mide en ausencia de un campo magnético. La cuantificación de la conductancia de campo cero y la transición suave al efecto Hall cuántico al aplicar un campo magnético son esencialmente consecuencias de la equipartición de la corriente entre un número entero de modos de propagación en la constricción.

Existen varias formas diferentes de fabricar un contacto puntual cuántico. Se puede realizar en una unión de ruptura separando un trozo de conductor hasta que se rompa. El punto de ruptura forma el contacto puntual. De una manera más controlada, los contactos puntuales cuánticos se forman en un gas de electrones bidimensional (2DEG), por ejemplo, en heteroestructuras de GaAs / AlGaAs . Al aplicar un voltaje a electrodos de compuerta con la forma adecuada, el gas de electrones se puede agotar localmente y se pueden crear muchos tipos diferentes de regiones conductoras en el plano del 2DEG, entre ellos puntos cuánticos y contactos puntuales cuánticos. Otro medio para crear un QPC es colocar la punta de un microscopio de efecto túnel cerca de la superficie de un conductor.

Geométricamente, un punto de contacto cuántico es una constricción en la dirección transversal que presenta una resistencia al movimiento de los electrones . La aplicación de un voltaje a través del punto de contacto induce el flujo de una corriente, la magnitud de esta corriente está dada por , donde es la conductancia del contacto. Esta fórmula se asemeja a la ley de Ohm para resistencias macroscópicas. Sin embargo, existe una diferencia fundamental aquí que resulta del pequeño tamaño del sistema que requiere un análisis mecánico cuántico. ^[7]${\estilo de visualización V}$${\displaystyle I=GV}$${\estilo de visualización G}$

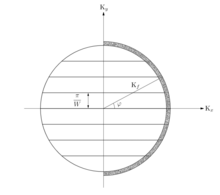
Lo más habitual es estudiar la QPC en gases de electrones bidimensionales. De esta manera, la constricción geométrica del punto de contacto convierte la conductancia a través de la abertura en un sistema unidimensional. Además, requiere una descripción mecánica cuántica del sistema que da como resultado la cuantificación de la conductancia. Desde el punto de vista mecánico cuántico, la corriente a través del punto de contacto se equiparticiona entre las subbandas unidimensionales o modos transversales en la constricción.

Es importante señalar que la discusión anterior no tiene en cuenta las posibles transiciones entre modos. La fórmula de Landauer puede, de hecho, generalizarse para expresar estas posibles transiciones.

${\displaystyle G={2e^{2} \sobre h}\suma _{n,m}|T_{n,m}|^{2}}$,

donde es la matriz de transición que incorpora probabilidades distintas de cero de transmisión del modo n a m .$Estilo de visualización T_{n,m}$

A bajas temperaturas y voltajes, los electrones no dispersos y no atrapados que contribuyen a la corriente tienen una cierta energía/momento/longitud de onda llamada energía de Fermi /momento/longitud de onda. Al igual que en una guía de ondas , el confinamiento transversal en el punto de contacto cuántico da como resultado una "cuantificación" del movimiento transversal: el movimiento transversal no puede variar de forma continua, sino que tiene que ser uno de una serie de modos discretos. La analogía de la guía de ondas es aplicable siempre que no se pierda la coherencia por dispersión, por ejemplo, por un defecto o un sitio de atrapamiento. La onda electrónica solo puede pasar a través de la constricción si interfiere de forma constructiva, lo que para un ancho de constricción dado, solo ocurre para un cierto número de modos . La corriente transportada por un estado cuántico de este tipo es el producto de la velocidad por la densidad de electrones. Estas dos cantidades por sí mismas difieren de un modo a otro, pero su producto es independiente del modo. Como consecuencia, cada estado contribuye con la misma cantidad de por dirección de espín a la conductancia total .${\estilo de visualización N}$$estilo de visualización e^{2}/h$$Estilo de visualización G=NG_{0}$

Este es un resultado fundamental; la conductancia no toma valores arbitrarios sino que se cuantifica en múltiplos del quantum de conductancia , que se expresa a través de la carga del electrón y la constante de Planck . El número entero está determinado por el ancho del punto de contacto y es aproximadamente igual al ancho dividido por la mitad de la longitud de onda del electrón . Como función del ancho del punto de contacto (o voltaje de compuerta en el caso de dispositivos de heteroestructura GaAs/AlGaAs), la conductancia muestra un comportamiento de escalera a medida que más y más modos (o canales) contribuyen al transporte de electrones. La altura del escalón está dada por .$Estilo de visualización G_{0}=2e^{2}/h$ ${\estilo de visualización e}$ ${\estilo de visualización h}$${\estilo de visualización N}$$Estilo de visualización GQ$

Al aumentar la temperatura, se observa experimentalmente que las mesetas adquieren una pendiente finita hasta que ya no se resuelven. Esto es una consecuencia del emborronamiento térmico de la distribución de Fermi-Dirac . Los pasos de conductancia deberían desaparecer para (aquí ∆ E es la división de subbandas en el nivel de Fermi ). Esto se confirma tanto experimentalmente como mediante cálculos numéricos. ^[9]${\displaystyle T\lesssim \Delta E/4k_{\rm {B}}\approx 4\;\mathrm {K} }$

Un campo magnético externo aplicado al punto de contacto cuántico eleva la degeneración del espín y conduce a pasos de semientero en la conductancia. Además, el número de modos que contribuyen se hace menor. Para campos magnéticos grandes, es independiente del ancho de la constricción, dada por la teoría del efecto Hall cuántico .${\estilo de visualización N}$${\estilo de visualización N}$

Las características anómalas en los pasos de conductancia cuantificados se observan a menudo en mediciones de transporte de contactos puntuales cuánticos. Un ejemplo notable es la meseta en , la llamada estructura 0,7, que surge debido a interacciones electrón-electrón mejoradas que surgen de una singularidad de van Hove difusa en la densidad local 1D de estados en la vecindad de la constricción de carga. ^[10] A diferencia de los pasos de conductancia, la estructura 0,7 se vuelve más pronunciada a mayor temperatura. A veces se observan análogos de la estructura 0,7 en pasos de conductancia más altos. Los estados cuasi-ligados que surgen de impurezas, trampas de carga y reflexiones dentro de la constricción también pueden dar como resultado una estructura de conductancia cercana al límite 1D.$estilo de visualización 0.7G_{Q}}$

Además de estudiar los fundamentos del transporte de carga en conductores mesoscópicos , los contactos puntuales cuánticos se pueden utilizar como detectores de carga extremadamente sensibles. Dado que la conductancia a través del contacto depende en gran medida del tamaño de la constricción, cualquier fluctuación potencial (por ejemplo, creada por otros electrones) en las proximidades influirá en la corriente a través del QPC. Es posible detectar electrones individuales con un esquema de este tipo. En vista de la computación cuántica en sistemas de estado sólido , los QPC se pueden utilizar como dispositivos de lectura para el estado de un bit cuántico (qubit). ^{[11] [12] [13] [14]} En física de dispositivos, la configuración de los QPC se utiliza para demostrar un transistor de efecto de campo completamente balístico. ^[15] Otra aplicación del dispositivo es su uso como interruptor. Un cable de níquel se acerca lo suficiente a una superficie de oro y luego, mediante el uso de un actuador piezoeléctrico, se puede cambiar la distancia entre el cable y la superficie y, por lo tanto, las características de transporte del dispositivo cambian entre tunelización de electrones y balística. ^[16]

• CWJBeenakker y H. van Houten (1991). "Transporte cuántico en nanoestructuras semiconductoras". Física del estado sólido . 44 : 1–228. arXiv : cond-mat/0412664 . Código Bibliográfico :2004cond.mat.12664B. doi :10.1016/s0081-1947(08)60091-0. ISBN 9780126077445.S2CID119082619  .​
• KJ Thomas; et al. (1996). "Posible polarización de espín en un gas de electrones unidimensional". Physical Review Letters . 77 (1): 135–138. arXiv : cond-mat/9606004 . Código Bibliográfico :1996PhRvL..77..135T. doi :10.1103/PhysRevLett.77.135. PMID  10061790. S2CID  8903637.
• Nicolás Agraït; Alfredo Levy Yeyati; Jan M. van Ruitenbeek (2003). "Propiedades cuánticas de conductores de tamaño atómico". Physics Reports . 377 (2–3): 81. arXiv : cond-mat/0208239 . Código Bibliográfico :2003PhR...377...81A. doi :10.1016/S0370-1573(02)00633-6. S2CID  119409385.
• Timp, G. (1992). "Capítulo 3: ¿Cuándo un cable se convierte en una guía de ondas de electrones?". Semiconductors and Semimetals Volumen 35. Vol. 35. págs. 113–190. doi :10.1016/S0080-8784(08)62393-5. ISBN 9780127521350.