Unidad aritmética lógica

| Parte de una serie sobre | |||||||
| Circuitos lógicos aritméticos | |||||||
|---|---|---|---|---|---|---|---|
| Navegación rápida | |||||||
Componentes
| |||||||
See also | |||||||
En informática , una unidad lógica aritmética ( ALU ) es un circuito digital combinacional que realiza operaciones aritméticas y de bits en números binarios enteros . [1] [2] Esto contrasta con una unidad de punto flotante (FPU), que opera con números de punto flotante . Es un componente fundamental de muchos tipos de circuitos informáticos, incluida la unidad central de procesamiento (CPU) de las computadoras, las FPU y las unidades de procesamiento gráfico (GPU). [3]
Las entradas de una ALU son los datos sobre los que se va a operar, denominados operandos , y un código que indica la operación que se va a realizar; la salida de la ALU es el resultado de la operación realizada. En muchos diseños, la ALU también tiene entradas o salidas de estado, o ambas, que transmiten información sobre una operación anterior o la operación actual, respectivamente, entre la ALU y los registros de estado externos .
Señales
Una ALU tiene una variedad de redes de entrada y salida , que son los conductores eléctricos que se utilizan para transmitir señales digitales entre la ALU y los circuitos externos. Cuando una ALU está en funcionamiento, los circuitos externos aplican señales a las entradas de la ALU y, en respuesta, la ALU produce y transmite señales a los circuitos externos a través de sus salidas.
Datos
Una ALU básica tiene tres buses de datos paralelos que constan de dos operandos de entrada ( A y B ) y una salida de resultado ( Y ). Cada bus de datos es un grupo de señales que transmite un número entero binario. Normalmente, los anchos de bus A, B e Y (la cantidad de señales que componen cada bus) son idénticos y coinciden con el tamaño de palabra nativo del circuito externo (por ejemplo, la CPU encapsulante u otro procesador).
Código de operación
La entrada del código de operación es un bus paralelo que transmite a la ALU un código de selección de operación, que es un valor enumerado que especifica la operación aritmética o lógica que la ALU debe realizar. El tamaño del código de operación (su ancho de bus) determina la cantidad máxima de operaciones distintas que la ALU puede realizar; por ejemplo, un código de operación de cuatro bits puede especificar hasta dieciséis operaciones diferentes de la ALU. En general, un código de operación de la ALU no es lo mismo que un código de operación en lenguaje de máquina , aunque en algunos casos puede estar codificado directamente como un campo de bits dentro de un código de operación en lenguaje de máquina.
Estado
Salidas
Las salidas de estado son varias señales individuales que transmiten información complementaria sobre el resultado de la operación actual de la ALU. Las ALU de uso general suelen tener señales de estado como:
- Carry-out , que transmite el acarreo resultante de una operación de suma, el préstamo resultante de una operación de resta o el bit de desbordamiento resultante de una operación de desplazamiento binario.
- Cero , que indica que todos los bits de Y son cero lógico.
- Negativo , que indica que el resultado de una operación aritmética es negativo.
- Desbordamiento , que indica que el resultado de una operación aritmética ha excedido el rango numérico de Y.
- Paridad , que indica si un número par o impar de bits en Y son uno lógico.
Al finalizar cada operación de la ALU, las señales de salida de estado se almacenan generalmente en registros externos para que estén disponibles para futuras operaciones de la ALU (por ejemplo, para implementar aritmética de precisión múltiple ) o para controlar la ramificación condicional . La colección de registros de bits que almacenan las salidas de estado a menudo se tratan como un solo registro de múltiples bits, al que se hace referencia como "registro de estado" o "registro de código de condición".
Entradas
Las entradas de estado permiten que se proporcione información adicional a la ALU cuando se realiza una operación. Normalmente, se trata de un único bit de "entrada" que es la salida almacenada de una operación de la ALU anterior.
Funcionamiento del circuito
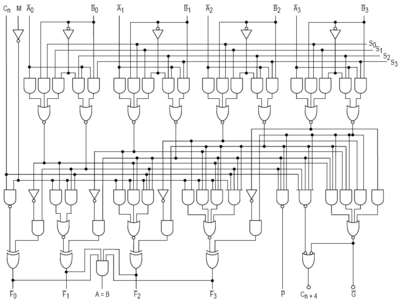
Una ALU es un circuito lógico combinacional , lo que significa que sus salidas cambiarán de forma asincrónica en respuesta a los cambios de entrada. En el funcionamiento normal, se aplican señales estables a todas las entradas de la ALU y, cuando ha transcurrido suficiente tiempo (conocido como " retardo de propagación ") para que las señales se propaguen a través de los circuitos de la ALU, el resultado de la operación de la ALU aparece en las salidas de la ALU. El circuito externo conectado a la ALU es responsable de garantizar la estabilidad de las señales de entrada de la ALU durante toda la operación y de permitir que transcurra suficiente tiempo para que las señales se propaguen a través de la ALU antes de muestrear el resultado de la ALU.
En general, los circuitos externos controlan una ALU aplicando señales a sus entradas. Normalmente, los circuitos externos emplean lógica secuencial para controlar el funcionamiento de la ALU, que se regula mediante una señal de reloj de una frecuencia lo suficientemente baja como para garantizar que las salidas de la ALU tengan tiempo suficiente para estabilizarse en las peores condiciones.
Por ejemplo, una CPU comienza una operación de suma de la ALU enrutando operandos desde sus fuentes (que normalmente son registros ) a las entradas de operandos de la ALU, mientras que la unidad de control aplica simultáneamente un valor a la entrada del código de operación de la ALU, configurándola para realizar la suma. Al mismo tiempo, la CPU también enruta la salida del resultado de la ALU a un registro de destino que recibirá la suma. Las señales de entrada de la ALU, que se mantienen estables hasta el siguiente reloj, pueden propagarse a través de la ALU y al registro de destino mientras la CPU espera el siguiente reloj. Cuando llega el siguiente reloj, el registro de destino almacena el resultado de la ALU y, dado que la operación de la ALU se ha completado, las entradas de la ALU pueden configurarse para la siguiente operación de la ALU.
Funciones
Las ALU suelen admitir una serie de funciones aritméticas básicas y lógicas bit a bit. Las ALU básicas de propósito general suelen incluir estas operaciones en sus repertorios: [1] [2] [4]
Operaciones aritméticas
- Suma : Se suman A y B y la suma aparece en Y y se lleva a cabo.
- Suma con acarreo : A, B y acarreo de entrada se suman y la suma aparece en Y y acarreo de salida.
- Restar : B se resta de A (o viceversa) y la diferencia aparece en Y y en el carry-out. Para esta función, el carry-out es efectivamente un indicador de "préstamo". Esta operación también se puede utilizar para comparar las magnitudes de A y B; en tales casos, el procesador puede ignorar la salida Y, al que solo le interesan los bits de estado (en particular, cero y negativo) que resultan de la operación.
- Restar con préstamo : B se resta de A (o viceversa) con préstamo (carry-in) y la diferencia aparece en Y y carry-out (borrow out).
- Complemento a dos : se resta A (o B) de cero y la diferencia aparece en Y.
- Incremento : A (o B) se incrementa en uno y el valor resultante aparece en Y.
- Decremento : A (o B) se disminuye en uno y el valor resultante aparece en Y.
- Paso a través : todos los bits de A (o B) aparecen sin modificar en Y. Esta operación se utiliza normalmente para determinar la paridad del operando o si es cero o negativo, o para cargar el operando en un registro del procesador.
Operaciones lógicas bit a bit
- AND : el AND bit a bit de A y B aparece en Y.
- OR : el OR bit a bit de A y B aparece en Y.
- OR exclusivo : la operación XOR bit a bit de A y B aparece en Y.
- Complemento a uno : todos los bits de A (o B) están invertidos y aparecen en Y.
Operaciones de desplazamiento de bits
| Tipo | Izquierda | Bien |
|---|---|---|
| Desplazamiento aritmético |  |  |
| Cambio lógico |  |  |
| Girar |  |  |
| Girar a través del transporte |  |  |
Las operaciones de desplazamiento de ALU hacen que el operando A (o B) se desplace hacia la izquierda o hacia la derecha (según el código de operación) y el operando desplazado aparece en Y. Las ALU simples normalmente pueden desplazar el operando solo una posición de bit, mientras que las ALU más complejas emplean desplazadores de barril que les permiten desplazar el operando una cantidad arbitraria de bits en una operación. En todas las operaciones de desplazamiento de un solo bit, el bit desplazado fuera del operando aparece en la ejecución; el valor del bit desplazado dentro del operando depende del tipo de desplazamiento.
- Desplazamiento aritmético : el operando se trata como un entero en complemento a dos , lo que significa que el bit más significativo es un bit de "signo" y se conserva.
- Desplazamiento lógico : se desplaza un cero lógico hacia el interior del operando. Esto se utiliza para desplazar números enteros sin signo.
- Rotar : el operando se trata como un buffer circular de bits, de modo que sus bits menos y más significativos son efectivamente adyacentes.
- Rotar a través del acarreo : el bit de acarreo y el operando se tratan colectivamente como un búfer circular de bits.
Aplicaciones
Aritmética de precisión múltiple
En los cálculos aritméticos de números enteros, la aritmética de precisión múltiple es un algoritmo que opera con números enteros que son más grandes que el tamaño de palabra de la ALU. Para ello, el algoritmo trata cada operando como una colección ordenada de fragmentos del tamaño de la ALU, ordenados desde el más significativo (MS) hasta el menos significativo (LS) o viceversa. Por ejemplo, en el caso de una ALU de 8 bits, el entero de 24 bits 0x123456se trataría como una colección de tres fragmentos de 8 bits: 0x12(MS), 0x34y 0x56(LS). Dado que el tamaño de un fragmento coincide exactamente con el tamaño de palabra de la ALU, la ALU puede operar directamente sobre este "fragmento" de operando.
El algoritmo utiliza la ALU para operar directamente sobre fragmentos de operandos particulares y así generar un fragmento correspondiente (un "parcial") del resultado de precisión múltiple. Cada parcial, cuando se genera, se escribe en una región asociada de almacenamiento que se ha designado para el resultado de precisión múltiple. Este proceso se repite para todos los fragmentos de operandos a fin de generar una colección completa de parciales, que es el resultado de la operación de precisión múltiple.
En las operaciones aritméticas (por ejemplo, suma, resta), el algoritmo comienza invocando una operación ALU en los fragmentos LS de los operandos, produciendo así un parcial LS y un bit de ejecución. El algoritmo escribe el parcial en el almacenamiento designado, mientras que la máquina de estados del procesador normalmente almacena el bit de ejecución en un registro de estado ALU. A continuación, el algoritmo avanza al siguiente fragmento de la colección de cada operando e invoca una operación ALU en estos fragmentos junto con el bit de ejecución almacenado de la operación ALU anterior, produciendo así otro parcial (más significativo) y un bit de ejecución. Como antes, el bit de ejecución se almacena en el registro de estado y el parcial se escribe en el almacenamiento designado. Este proceso se repite hasta que se hayan procesado todos los fragmentos de operandos, lo que da como resultado una colección completa de parciales en el almacenamiento, que comprenden el resultado aritmético de precisión múltiple.
En las operaciones de desplazamiento de precisión múltiple, el orden de procesamiento de los fragmentos de operandos depende de la dirección del desplazamiento. En las operaciones de desplazamiento a la izquierda, los fragmentos se procesan primero en sentido inverso porque el bit LS de cada parcial (que se transmite a través del bit de acarreo almacenado) debe obtenerse del bit MS del operando desplazado a la izquierda y menos significativo anteriormente. Por el contrario, los operandos se procesan primero en sentido inverso en las operaciones de desplazamiento a la derecha porque el bit MS de cada parcial debe obtenerse del bit LS del operando desplazado a la derecha y más significativo anteriormente.
En operaciones lógicas bit a bit (por ejemplo, AND lógico, OR lógico), los fragmentos de operandos se pueden procesar en cualquier orden arbitrario porque cada parcial depende únicamente de los fragmentos de operandos correspondientes (se ignora el bit de acarreo almacenado de la operación ALU anterior).
Operaciones complejas
Aunque una ALU puede diseñarse para realizar funciones complejas, la mayor complejidad del circuito, el costo, el consumo de energía y el mayor tamaño resultantes hacen que esto sea poco práctico en muchos casos. En consecuencia, las ALU a menudo se limitan a funciones simples que se pueden ejecutar a velocidades muy altas (es decir, retrasos de propagación muy cortos), y el circuito del procesador externo es responsable de realizar funciones complejas al orquestar una secuencia de operaciones de ALU más simples.
Por ejemplo, el cálculo de la raíz cuadrada de un número se puede implementar de varias maneras, dependiendo de la complejidad de la ALU:
- Cálculo en un solo reloj : una ALU muy compleja que calcula una raíz cuadrada en una sola operación.
- Canalización de cálculo : un grupo de ALU simples que calculan una raíz cuadrada en etapas, con resultados intermedios que pasan por ALUs dispuestas como una línea de producción de una fábrica . Este circuito puede aceptar nuevos operandos antes de terminar los anteriores y produce resultados tan rápido como la ALU muy compleja, aunque los resultados se retrasan por la suma de los retrasos de propagación de las etapas de la ALU. Para obtener más información, consulte el artículo sobre canalización de instrucciones .
- Cálculo iterativo : una ALU simple que calcula la raíz cuadrada a través de varios pasos bajo la dirección de una unidad de control .
Las implementaciones anteriores pasan de la más rápida y costosa a la más lenta y económica. La raíz cuadrada se calcula en todos los casos, pero los procesadores con ALU simples tardarán más en realizar el cálculo porque se deben realizar múltiples operaciones de ALU.
Implementación
Una ALU se suele implementar como un circuito integrado (CI) independiente , como el 74181 , o como parte de un CI más complejo. En este último caso, una ALU se suele instanciar sintetizándola a partir de una descripción escrita en VHDL , Verilog o algún otro lenguaje de descripción de hardware . Por ejemplo, el siguiente código VHDL describe una ALU de 8 bits muy simple :
entidad alu es puerto ( -- las conexiones a circuitos externos: A : in signed ( 7 downto 0 ); -- operando A B : in signed ( 7 downto 0 ); -- operando B OP : in unsigned ( 2 downto 0 ); -- código de operación Y : out signed ( 7 downto 0 )); -- resultado de la operación end alu ; arquitectura conductual de alu es begin case OP es -- decodificar el opcode y realizar la operación: cuando "000" => Y <= A + B ; -- sumar cuando "001" => Y <= A - B ; -- restar cuando "010" => Y <= A - 1 ; -- decrementar cuando "011" => Y <= A + 1 ; -- incrementar cuando "100" => Y <= no A ; -- complemento a 1 cuando "101" => Y <= A y B ; -- AND bit a bit cuando "110" => Y <= A o B ; -- OR bit a bit cuando "111" => Y < = A xor B ; -- XOR bit a bit cuando otros => Y <= ( otros => 'X' ); fin de caso ; fin conductual ; Historia
El matemático John von Neumann propuso el concepto de ALU en 1945 en un informe sobre las bases de una nueva computadora llamada EDVAC . [5]
El costo, el tamaño y el consumo de energía de los circuitos electrónicos eran relativamente altos durante los inicios de la era de la información . En consecuencia, todas las primeras computadoras tenían una ALU en serie que operaba con un bit de datos a la vez, aunque a menudo presentaban un tamaño de palabra más amplio a los programadores. La primera computadora en tener múltiples circuitos ALU discretos de un solo bit en paralelo fue la Whirlwind I de 1951 , que empleaba dieciséis de esas "unidades matemáticas" para poder operar con palabras de 16 bits.
En 1967, Fairchild presentó el primer dispositivo tipo ALU implementado como circuito integrado, el Fairchild 3800, que consistía en una unidad aritmética de ocho bits con acumulador. Solo admitía sumas y restas, pero no funciones lógicas. [6]
Pronto surgieron las ALU de circuito integrado completo, incluidas las ALU de cuatro bits como la Am2901 y la 74181. Estos dispositivos eran típicamente capaces de " bit slice ", lo que significa que tenían señales de "acarreo anticipado" que facilitaban el uso de múltiples chips ALU interconectados para crear una ALU con un tamaño de palabra más amplio. Estos dispositivos rápidamente se hicieron populares y fueron ampliamente utilizados en minicomputadoras de bit slice.
Los microprocesadores comenzaron a aparecer a principios de la década de 1970. Aunque los transistores se habían vuelto más pequeños, a veces no había suficiente espacio en la matriz para una ALU de ancho de palabra completo y, como resultado, algunos de los primeros microprocesadores emplearon una ALU estrecha que requería múltiples ciclos por instrucción de lenguaje de máquina. Ejemplos de esto incluyen el popular Zilog Z80 , que realizaba sumas de ocho bits con una ALU de cuatro bits. [7] Con el tiempo, las geometrías de los transistores se redujeron aún más, siguiendo la ley de Moore , y se hizo factible construir ALU más anchas en microprocesadores.
Los transistores de los circuitos integrados (CI) modernos son órdenes de magnitud más pequeños que los de los primeros microprocesadores, lo que permite incorporar unidades de procesamiento de señales altamente complejas en los CI. En la actualidad, muchas unidades de procesamiento de señales modernas tienen anchos de palabra amplios y mejoras arquitectónicas, como desplazadores de barril y multiplicadores binarios , que les permiten realizar, en un solo ciclo de reloj, operaciones que habrían requerido múltiples operaciones en las unidades de procesamiento de señales anteriores.
Las ALU se pueden realizar como circuitos mecánicos , electromecánicos o electrónicos [8] [ verificación fallida ] y, en los últimos años, se han llevado a cabo investigaciones sobre ALU biológicas [9] [10] (por ejemplo, basadas en actina ). [11]
Véase también
- Sumador (electrónica)
- Unidad de generación de direcciones (UGD)
- Unidad de carga y almacenamiento
- Multiplicador binario
- Unidad de ejecución
Referencias
- ^ por Atul P. Godse; Deepali A. Godse (2009). "3". Diseño de lógica digital . Publicaciones técnicas. págs. 9-3. ISBN 978-81-8431-738-1.[ enlace muerto permanente ]
- ^ de Atul P. Godse; Deepali A. Godse (2009). "Apéndice". Circuitos lógicos digitales. Publicaciones técnicas. págs. C–1. ISBN 978-81-8431-650-6.[ enlace muerto permanente ]
- ^ "1. Introducción a la arquitectura informática: diseño de hardware integrado, 2.ª edición [libro]". www.oreilly.com . Consultado el 3 de septiembre de 2020 .
- ^ Horowitz, Paul ; Winfield Hill (1989). "14.1.1". El arte de la electrónica (2.ª ed.). Cambridge University Press. págs. 990–. ISBN 978-0-521-37095-0.
- ^ Philip Levis (8 de noviembre de 2004). «Jonathan von Neumann y EDVAC» (PDF) . cs.berkeley.edu . pp. 1, 3. Archivado desde el original (PDF) el 23 de septiembre de 2015. Consultado el 20 de enero de 2015 .
- ^ Sherriff, Ken. "Dentro del chip 74181 ALU: fotos de la matriz e ingeniería inversa". Blog de Ken Shirriff . Consultado el 7 de mayo de 2024 .
- ^ Ken Shirriff. "El Z-80 tiene una ALU de 4 bits. Así es como funciona". 2013, righto.com
- ^ Reif, John H. (2009), "Computación mecánica: la complejidad computacional de los dispositivos físicos", en Meyers, Robert A. (ed.), Enciclopedia de complejidad y ciencia de sistemas , Nueva York, NY: Springer, págs. 5466–5482, doi :10.1007/978-0-387-30440-3_325, ISBN 978-0-387-30440-3, consultado el 3 de septiembre de 2020
- ^ Lin, Chun-Liang; Kuo, Ting-Yu; Li, Wei-Xian (14 de agosto de 2018). "Síntesis de la unidad de control para la futura biocomputadora". Revista de ingeniería biológica . 12 (1): 14. doi : 10.1186/s13036-018-0109-4 . ISSN 1754-1611. PMC 6092829 . PMID 30127848.
- ^ Gerd Hg Moe-Behrens. "El microprocesador biológico, o cómo construir un ordenador con componentes biológicos".
- ^ Das, Biplab; Paul, Avijit Kumar; De, Debashis (16 de agosto de 2019). "Diseño y cálculo de una unidad lógica aritmética no convencional en autómatas celulares cuánticos de actina". Microsystem Technologies . 28 (3): 809–822. doi :10.1007/s00542-019-04590-1. ISSN 1432-1858. S2CID 202099203.
Lectura adicional
- Hwang, Enoch (2006). Lógica digital y diseño de microprocesadores con VHDL. Thomson. ISBN 0-534-46593-5.
- Stallings, William (2006). Organización y arquitectura de computadoras: diseño para el rendimiento (7.ª ed.). Pearson Prentice Hall. ISBN 0-13-185644-8.
