Módulo
En informática , la operación módulo devuelve el resto o resto con signo de una división , después de dividir un número por otro, llamado módulo de la operación.
Dados dos números positivos a y n , a módulo n (a menudo abreviado como a mod n ) es el resto de la división euclidiana de a por n , donde a es el dividendo y n es el divisor . [1]
Por ejemplo, la expresión "5 mod 2" evalúa a 1, porque 5 dividido por 2 tiene un cociente de 2 y un resto de 1, mientras que "9 mod 3" evaluaría a 0, porque 9 dividido por 3 tiene un cociente de 3 y un resto de 0.
Aunque normalmente se realiza con a y n , ambos enteros , muchos sistemas informáticos ahora permiten otros tipos de operandos numéricos. El rango de valores para una operación de módulo entero de n es de 0 a n − 1 ( un módulo 1 siempre es 0; un módulo 0 no está definido, ya que es una división por cero ).
Cuando exactamente uno de a o n es negativo, la definición básica no funciona y los lenguajes de programación difieren en cómo se definen estos valores.
Variantes de la definición
En matemáticas , el resultado de la operación módulo es una clase de equivalencia , y cualquier miembro de la clase puede elegirse como representante ; sin embargo, el representante habitual es el residuo positivo más pequeño , el entero no negativo más pequeño que pertenece a esa clase (es decir, el resto de la división euclidiana ). [2] Sin embargo, son posibles otras convenciones. Las computadoras y las calculadoras tienen varias formas de almacenar y representar números; por lo tanto, su definición de la operación módulo depende del lenguaje de programación o del hardware subyacente .
En casi todos los sistemas informáticos, el cociente q y el resto r de a dividido por n satisfacen las siguientes condiciones:
| ( 1 ) |
Esto todavía deja una ambigüedad de signo si el resto no es cero: hay dos opciones posibles para el resto, una negativa y la otra positiva; esa elección determina cuál de los dos cocientes consecutivos debe usarse para satisfacer la ecuación (1). En teoría de números, siempre se elige el resto positivo, pero en informática, los lenguajes de programación eligen dependiendo del lenguaje y de los signos de a o n . [a] Pascal estándar y ALGOL 68 , por ejemplo, dan un resto positivo (o 0) incluso para divisores negativos, y algunos lenguajes de programación, como C90, lo dejan a la implementación cuando cualquiera de n o a es negativo (ver la tabla en § En lenguajes de programación para más detalles). a módulo 0 no está definido en la mayoría de los sistemas, aunque algunos lo definen como a .

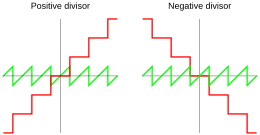
Cociente ( q ) y resto ( r ) en función del dividendo ( a ), utilizando división truncada Muchas implementaciones utilizan la división truncada , para la cual el cociente se define mediante
donde es la función de la parte integral ( redondeo hacia cero ), es decir, el truncamiento a cero de dígitos significativos. Por lo tanto, según la ecuación ( 1 ), el resto tiene el mismo signo que el dividendo a, por lo que puede tomar 2| n | − 1 valores:

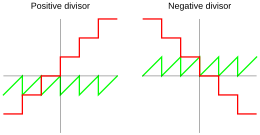
Cociente y resto utilizando división por pisos Donald Knuth [3] promueve la división por pisos , para la cual el cociente se define por
donde es la función suelo ( redondeo hacia abajo ). Por lo tanto, según la ecuación ( 1 ), el resto tiene el mismo signo que el divisor n :

Cociente y resto mediante división euclidiana Raymond T. Boute [4] promueve la división euclidiana , para la cual el cociente se define por
donde sgn es la función de signo , es la función de suelo ( redondeando hacia abajo ) y es la función de techo ( redondeando hacia arriba ). Por lo tanto, según la ecuación ( 1 ), el resto no es negativo :

Cociente y resto utilizando división redondeada Common Lisp e IEEE 754 utilizan la división redondeada , para la cual el cociente se define por
donde round es la función round ( redondear la mitad a par ). Por lo tanto, según la ecuación ( 1 ), el resto se encuentra entre y , y su signo depende de qué lado del cero se encuentre dentro de estos límites:

Cociente y resto utilizando división de techo Common Lisp también utiliza la división de techo , para la cual el cociente se define por
donde ⌈⌉ es la función techo ( redondeando hacia arriba ). Por lo tanto, según la ecuación ( 1 ), el resto tiene el signo opuesto al del divisor :
Si tanto el dividendo como el divisor son positivos, entonces las definiciones truncadas, con límite inferior y euclidianas coinciden. Si el dividendo es positivo y el divisor es negativo, entonces las definiciones truncadas y euclidianas coinciden. Si el dividendo es negativo y el divisor es positivo, entonces las definiciones con límite inferior y euclidianas coinciden. Si tanto el dividendo como el divisor son negativos, entonces las definiciones truncadas y con límite inferior coinciden.
Como lo describe Leijen,
Boute sostiene que la división euclidiana es superior a las demás en términos de regularidad y propiedades matemáticas útiles, aunque la división por pisos, promovida por Knuth, también es una buena definición. A pesar de su uso generalizado, se demuestra que la división truncada es inferior a las demás definiciones.
— Daan Leijen, División y módulo para científicos informáticos [5]
Sin embargo, la división truncada satisface la identidad . [6]
Notación
Algunas calculadoras tienen un botón de función mod() y muchos lenguajes de programación tienen una función similar, expresada como mod( a , n ) , por ejemplo. Algunas también admiten expresiones que utilizan "%", "mod" o "Mod" como operador de módulo o resto , como a % no a mod n.
Para entornos que carecen de una función similar, se puede utilizar cualquiera de las tres definiciones anteriores.
Errores comunes
Cuando el resultado de una operación módulo tiene el signo del dividendo (definición truncada), puede dar lugar a errores sorprendentes.
Por ejemplo, para probar si un número entero es impar , uno podría inclinarse a probar si el resto por 2 es igual a 1:
bool is_odd ( int n ) { devolver n % 2 == 1 ; } Pero en un lenguaje donde el módulo tiene el signo del dividendo, eso es incorrecto, porque cuando n (el dividendo) es negativo e impar, n mod 2 devuelve −1, y la función devuelve falso.
Una alternativa correcta es probar que el resto no es 0 (porque el resto 0 es el mismo independientemente de los signos):
bool is_odd ( int n ) { devuelve n % 2 != 0 ; } Problemas de rendimiento
Las operaciones de módulo se pueden implementar de manera que cada vez se calcule una división con un resto. Para casos especiales, en algunos equipos existen alternativas más rápidas. Por ejemplo, el módulo de potencias de 2 se puede expresar alternativamente como una operación AND bit a bit (suponiendo que x es un entero positivo o utilizando una definición que no trunque):
x % 2n == x & (2n - 1)
Ejemplos:
x % 2 == x & 1x % 4 == x & 3x % 8 == x & 7
En dispositivos y software que implementan operaciones bit a bit de manera más eficiente que el módulo, estas formas alternativas pueden dar como resultado cálculos más rápidos. [7]
Las optimizaciones del compilador pueden reconocer expresiones de la forma expression % constantdonde constantes una potencia de dos e implementarlas automáticamente como expression & (constant-1), lo que permite al programador escribir código más claro sin comprometer el rendimiento. Esta optimización simple no es posible para lenguajes en los que el resultado de la operación módulo tiene el signo del dividendo (incluido C ), a menos que el dividendo sea de un tipo entero sin signo . Esto se debe a que, si el dividendo es negativo, el módulo será negativo, mientras que expression & (constant-1)siempre será positivo. Para estos lenguajes, se debe utilizar la equivalencia, expresada mediante operaciones OR, NOT y AND bit a bit.x % 2n == x < 0 ? x | ~(2n - 1) : x & (2n - 1)
También existen optimizaciones para operaciones generales de módulo constante calculando primero la división utilizando la optimización del divisor constante .
Propiedades (identidades)
Algunas operaciones de módulo se pueden factorizar o expandir de forma similar a otras operaciones matemáticas. Esto puede resultar útil en pruebas criptográficas , como el intercambio de claves Diffie-Hellman . Las propiedades que implican multiplicación, división y exponenciación generalmente requieren que a y n sean números enteros.
- Identidad:
- ( a mod n ) mod n = a mod n .
- n x mod n = 0 para todos los valores enteros positivos de x .
- Si p es un número primo que no es divisor de b , entonces ab p −1 mod p = a mod p , debido al pequeño teorema de Fermat .
- Inverso:
- [(− a mod n ) + ( a mod n )] mod n = 0 .
- b −1 mod n denota el inverso multiplicativo modular , que se define si y solo si b y n son primos entre sí , lo que es el caso cuando se define el lado izquierdo: [( b −1 mod n )( b mod n )] mod n = 1 .
- Distributivo:
- ( a + b ) módulo n = [( a módulo n ) + ( b módulo n )] módulo n .
- ab mod n = [( a mod n )( b mod n )] mod n .
- División (definición): a/bmod n = [( a mod n )( b −1 mod n )] mod n , cuando el lado derecho está definido (es decir, cuando b y n son coprimos ) , y no está definido en caso contrario.
- Multiplicación inversa: [( ab mod n )( b −1 mod n )] mod n = a mod n .
En lenguajes de programación
| Idioma | Operador | Entero | Punto flotante | Definición |
|---|---|---|---|---|
| ABAP | MOD | Sí | Sí | Euclidiano |
| Script de acción | % | Sí | No | Truncado |
| Ada | mod | Sí | No | Piso [8] |
rem | Sí | No | Truncado [8] | |
| ALGOL 68 | ÷×,mod | Sí | No | Euclidiano |
| AMPL | mod | Sí | No | Truncado |
| APL | |[b] | Sí | Sí | Piso |
| Script de Apple | mod | Sí | No | Truncado |
| AutoLISP | (rem d n) | Sí | No | Truncado |
| AWK | % | Sí | No | Truncado |
| intento | % | Sí | No | Truncado |
| BÁSICO | Mod | Sí | No | Varía según la implementación |
| antes de Cristo | % | Sí | No | Truncado |
| C C++ | %,div | Sí | No | Truncado [c] |
fmod(C) std::fmod(C++) | No | Sí | Truncado [11] | |
remainder(C) std::remainder(C++) | No | Sí | Redondeado | |
| DO# | % | Sí | Sí | Truncado |
Math.IEEERemainder | No | Sí | Redondeado [12] | |
| Clarín | % | Sí | No | Truncado |
| Limpio | rem | Sí | No | Truncado |
| Clojure | mod | Sí | No | Piso [13] |
rem | Sí | No | Truncado [14] | |
| COBOL | FUNCTION MOD | Sí | No | Piso [15] |
FUNCTION REM | Sí | Sí | Truncado [15] | |
| Script de café | % | Sí | No | Truncado |
%% | Sí | No | Piso [16] | |
| Fusión fría | %,MOD | Sí | No | Truncado |
| Lenguaje Intermedio Común | rem(firmado) | Sí | Sí | Truncado [17] |
rem.un(no firmado) | Sí | No | — | |
| Ceceo común | mod | Sí | Sí | Piso |
rem | Sí | Sí | Truncado | |
| Cristal | %,modulo | Sí | Sí | Piso |
remainder | Sí | Sí | Truncado | |
| CSS | mod() | Sí | Sí | Piso [18] |
rem() | Sí | Sí | Truncado [19] | |
| D | % | Sí | Sí | Truncado [20] |
| Dardo | % | Sí | Sí | Euclidiana [21] |
remainder() | Sí | Sí | Truncado [22] | |
| Torre Eiffel | \\ | Sí | No | Truncado |
| Elixir | rem/2 | Sí | No | Truncado [23] |
Integer.mod/2 | Sí | No | Piso [24] | |
| Olmo | modBy | Sí | No | Piso [25] |
remainderBy | Sí | No | Truncado [26] | |
| Erlang | rem | Sí | No | Truncado |
math:fmod/2 | No | Sí | Truncado (igual que C) [27] | |
| Euforia | mod | Sí | No | Piso |
remainder | Sí | No | Truncado | |
| F# | % | Sí | Sí | Truncado |
Math.IEEERemainder | No | Sí | Redondeado [12] | |
| Factor | mod | Sí | No | Truncado |
| Creador de archivos | Mod | Sí | No | Piso |
| Adelante | mod | Sí | No | Definición de implementación |
fm/mod | Sí | No | Piso | |
sm/rem | Sí | No | Truncado | |
| Fortran | mod | Sí | Sí | Truncado |
modulo | Sí | Sí | Piso | |
| friki | mod | Sí | No | Piso |
| BÁSICO completo | MOD | Sí | Sí | Piso [28] |
REMAINDER | Sí | Sí | Truncado [29] | |
| GLSL | % | Sí | No | Indefinido [30] |
mod | No | Sí | Piso [31] | |
| Estudio GameMaker (GML) | mod,% | Sí | No | Truncado |
| GDScript (Godot) | % | Sí | No | Truncado |
fmod | No | Sí | Truncado | |
posmod | Sí | No | Euclidiano | |
fposmod | No | Sí | Euclidiano | |
| Ir | % | Sí | No | Truncado [32] |
math.Mod | No | Sí | Truncado [33] | |
big.Int.Mod | Sí | No | Euclidiana [34] | |
big.Int.Rem | Sí | No | Truncado [35] | |
| Genial | % | Sí | No | Truncado |
| Haskell | mod | Sí | No | Piso [36] |
rem | Sí | No | Truncado [36] | |
Data.Fixed.mod'( GHC- H) | No | Sí | Piso | |
| Hacha | % | Sí | No | Truncado |
| Nivel de inglés alto y medio | % | Sí | Sí | Indefinido [37] |
| Yo | |[b] | Sí | No | Piso |
| Java | % | Sí | Sí | Truncado |
Math.floorMod | Sí | No | Piso | |
| Tipografía de JavaScript | % | Sí | Sí | Truncado |
| Julia | mod | Sí | Sí | Piso [38] |
%,rem | Sí | Sí | Truncado [39] | |
| Kotlin | %,rem | Sí | Sí | Truncado [40] |
mod | Sí | Sí | Piso [41] | |
| ksh | % | Sí | No | Truncado (igual que POSIX sh) |
fmod | No | Sí | Truncado | |
| LabVIEW | mod | Sí | Sí | Truncado |
| LibreOffice | =MOD() | Sí | No | Piso |
| Logo | MODULO | Sí | No | Piso |
REMAINDER | Sí | No | Truncado | |
| Lua 5 | % | Sí | Sí | Piso |
| Lua 4 | mod(x,y) | Sí | Sí | Truncado |
| Libertad BÁSICA | MOD | Sí | No | Truncado |
| Matemáticas cad | mod(x,y) | Sí | No | Piso |
| Arce | e mod m(por defecto),modp(e, m) | Sí | No | Euclidiano |
mods(e, m) | Sí | No | Redondeado | |
frem(e, m) | Sí | Sí | Redondeado | |
| Matemática | Mod[a, b] | Sí | No | Piso |
| MATLAB | mod | Sí | No | Piso |
rem | Sí | No | Truncado | |
| Máxima | mod | Sí | No | Piso |
remainder | Sí | No | Truncado | |
| Lenguaje integrado Maya | % | Sí | No | Truncado |
| Microsoft Excel | =MOD() | Sí | Sí | Piso |
| Minitab | MOD | Sí | No | Piso |
| Módulo-2 | MOD | Sí | No | Piso |
REM | Sí | No | Truncado | |
| PAPERAS | # | Sí | No | Piso |
| Ensamblador de red ( NASM , NASMX ) | %, div(sin firmar) | Sí | No | — |
%%(firmado) | Sí | No | Definido por la implementación [42] | |
| Nim | mod | Sí | No | Truncado |
| Oberón | MOD | Sí | No | Con forma de suelo [d] |
| Objetivo-C | % | Sí | No | Truncado (igual que C99) |
| Objeto Pascal , Delphi | mod | Sí | No | Truncado |
| OCaml | mod | Sí | No | Truncado [43] |
mod_float | No | Sí | Truncado [44] | |
| Occam | \ | Sí | No | Truncado |
| Pascal (ISO-7185 y -10206) | mod | Sí | No | De tipo euclidiano [e] |
| Perl | % | Sí | No | Pisoteado [f] |
POSIX::fmod | No | Sí | Truncado | |
| Fix | mod | Sí | No | Piso |
remainder | Sí | No | Truncado | |
| PHP | % | Sí | No | Truncado [46] |
fmod | No | Sí | Truncado [47] | |
| PIC BASIC Pro | \\ | Sí | No | Truncado |
| PL/Yo | mod | Sí | No | Con piso (ANSI PL/I) |
| Potencia Shell | % | Sí | No | Truncado |
| Código de programación ( PRC ) | MATH.OP - 'MOD; (\)' | Sí | No | Indefinido |
| Progreso | modulo | Sí | No | Truncado |
| Prólogo (ISO 1995) | mod | Sí | No | Piso |
rem | Sí | No | Truncado | |
| Puro Básico | %,Mod(x,y) | Sí | No | Truncado |
| Puro Script | `mod` | Sí | No | Euclidiana [48] |
| Datos Puros | % | Sí | No | Truncado (igual que C) |
mod | Sí | No | Piso | |
| Pitón | % | Sí | Sí | Piso |
math.fmod | No | Sí | Truncado | |
math.remainder | No | Sí | Redondeado | |
| Pregunta# | % | Sí | No | Truncado [49] |
| R | %% | Sí | Sí | Piso [50] |
| Raqueta | modulo | Sí | No | Piso |
remainder | Sí | No | Truncado | |
| Raku | % | No | Sí | Piso |
| RealBásico | MOD | Sí | No | Truncado |
| Razón | mod | Sí | No | Truncado |
| Rexx | // | Sí | Sí | Truncado |
| Juego de rol | %REM | Sí | No | Truncado |
| Rubí | %,modulo() | Sí | Sí | Piso |
remainder() | Sí | Sí | Truncado | |
| Óxido | % | Sí | Sí | Truncado |
rem_euclid() | Sí | Sí | Euclidiana [51] | |
| SAS | MOD | Sí | No | Truncado |
| Escala | % | Sí | Sí | Truncado |
| Esquema | modulo | Sí | No | Piso |
remainder | Sí | No | Truncado | |
| Esquema R 6 RS | mod | Sí | No | Euclidiana [52] |
mod0 | Sí | No | Redondeado [52] | |
flmod | No | Sí | Euclidiano | |
flmod0 | No | Sí | Redondeado | |
| Rascar | mod | Sí | Sí | Piso |
| Semilla7 | mod | Sí | Sí | Piso |
rem | Sí | Sí | Truncado | |
| Hablar con sentido | modulo | Sí | No | Piso |
rem | Sí | No | Truncado | |
sh(POSIX) (incluye bash , mksh , etc.) | % | Sí | No | Truncado (igual que C) [53] |
| Charla informal | \\ | Sí | No | Piso |
rem: | Sí | No | Truncado | |
| ¡Quebrar! | mod | Sí | No | Piso |
| Girar | // | Sí | No | Piso |
| Solidez | % | Sí | No | Truncado [54] |
| SQL ( SQL:1999 ) | mod(x,y) | Sí | No | Truncado |
| SQL ( SQL:2011 ) | % | Sí | No | Truncado |
| ML estándar | mod | Sí | No | Piso |
Int.rem | Sí | No | Truncado | |
Real.rem | No | Sí | Truncado | |
| Estado | mod(x,y) | Sí | No | Euclidiano |
| Rápido | % | Sí | No | Truncado [55] |
remainder(dividingBy:) | No | Sí | Redondeado [56] | |
truncatingRemainder(dividingBy:) | No | Sí | Truncado [57] | |
| Tcl | % | Sí | No | Piso |
fmod() | No | Sí | Truncado (como C) | |
| Tcsh-español:Tcsh-español: | % | Sí | No | Truncado |
| Esfuerzo de torsión | % | Sí | No | Truncado |
| Turing | mod | Sí | No | Piso |
| Verilog (2001) | % | Sí | No | Truncado |
| VHDL | mod | Sí | No | Piso |
rem | Sí | No | Truncado | |
| VimL | % | Sí | No | Truncado |
| Visual Basic | Mod | Sí | No | Truncado |
| WebAsamblea | i32.rem_u, i64.rem_u(sin firmar) | Sí | No | — [58] |
i32.rem_s, i64.rem_s(firmado) | Sí | No | Truncado [58] | |
| Ensamblaje x86 | IDIV | Sí | No | Truncado |
| XBase++ | % | Sí | Sí | Truncado |
Mod() | Sí | Sí | Piso | |
| Zig | %,
| Sí | Sí | Truncado [59] |
| Demostrador del teorema Z3 | div,mod | Sí | No | Euclidiano |
Además, muchos sistemas informáticos proporcionan una divmodfunción que produce el cociente y el resto al mismo tiempo. Algunos ejemplos son la instrucción de la arquitectura x86IDIV , la función del lenguaje de programación C div()y la función de Pythondivmod() .
Generalizaciones
Módulo con desplazamiento
A veces resulta útil que el resultado de un módulo n no se encuentre entre 0 y n − 1 , sino entre algún número d y d + n − 1 . En ese caso, d se denomina desplazamiento y d = 1 es particularmente común.
No parece haber una notación estándar para esta operación, así que usemos tentativamente a mod d n . Tenemos entonces la siguiente definición: [60] x = a mod d n solo en caso de que d ≤ x ≤ d + n − 1 y x mod n = a mod n . Claramente, la operación módulo usual corresponde al desplazamiento cero: a mod n = a mod 0 n .
La operación de módulo con desplazamiento está relacionada con la función de piso de la siguiente manera:
Para ver esto, sea . Primero demostramos que x mod n = a mod n . En general, es cierto que ( a + bn ) mod n = a mod n para todos los enteros b ; por lo tanto, esto también es cierto en el caso particular cuando ; pero eso significa que , que es lo que queríamos demostrar. Queda por demostrar que d ≤ x ≤ d + n − 1 . Sean k y r los enteros tales que a − d = kn + r con 0 ≤ r ≤ n − 1 (ver división euclidiana ). Luego , por lo tanto . Ahora tome 0 ≤ r ≤ n − 1 y agregue d a ambos lados, obteniendo d ≤ d + r ≤ d + n − 1 . Pero hemos visto que x = d + r , así que hemos terminado.
El módulo con desplazamiento a mod d n se implementa en Mathematica como Mod[a, n, d] . [60]
Implementación de otras definiciones de módulo mediante truncamiento
A pesar de la elegancia matemática de la división por pisos de Knuth y de la división euclidiana, en general es mucho más común encontrar un módulo basado en una división truncada en los lenguajes de programación. Leijen proporciona los siguientes algoritmos para calcular las dos divisiones dada una división entera truncada: [5]
/* Divmod euclidiano y con piso, en el estilo de ldiv() de C */ typedef struct { /* Esta estructura es parte de C stdlib.h, pero se reproduce aquí para mayor claridad */ long int quot ; long int rem ; } ldiv_t ; /* División euclidiana */ inline ldiv_t ldivE ( long numer , long denom ) { /* Los lenguajes C99 y C++11 definen ambos como truncados. */ long q = numer / denom ; long r = numer % denom ; if ( r < 0 ) { if ( denom > 0 ) { q = q - 1 ; r = r + denom ; } else { q = q + 1 ; r = r - denom ; } } return ( ldiv_t ){. quot = q , .rem = r } ; } /* División por piso */ inline ldiv_t ldivF ( long numer , long denom ) { long q = numer / denom ; long r = numer % denom ; if (( r > 0 && denom < 0 ) || ( r < 0 && denom > 0 )) { q = q - 1 ; r = r + denom ; } return ( ldiv_t ){. quot = q , .rem = r } ; } En ambos casos, el resto se puede calcular independientemente del cociente, pero no al revés. En este caso, las operaciones se combinan para ahorrar espacio en la pantalla, ya que las ramas lógicas son las mismas.
Véase también
- Módulo (desambiguación) : muchos usos de la palabra módulo , todos los cuales surgieron a partir de la introducción de la aritmética modular por parte de Carl F. Gauss en 1801.
- Módulo (matemáticas) , uso general del término en matemáticas
- Exponenciación modular
- Giro (ángulo)
Notas
- ^ Matemáticamente, estas dos opciones son sólo dos del número infinito de opciones disponibles para la desigualdad satisfecha por un resto .
- ^ ab El orden de los argumentos se invierte, es decir,
α|ωcalcula , el resto al dividir por .ωα - ^ C99 y C++11 definen el comportamiento de
%que se debe truncar. [9] Los estándares anteriores dejan el comportamiento definido por la implementación. [10] - ^ El divisor debe ser positivo, de lo contrario no está definido.
- ^ Como lo analiza Boute, las definiciones de ISO Pascal de
divymodno obedecen la identidad de división de D = d · ( D / d ) + D % d , y por lo tanto están fundamentalmente rotas. - ^ Perl suele utilizar un operador de módulo aritmético que es independiente de la máquina. Para ver ejemplos y excepciones, consulte la documentación de Perl sobre operadores multiplicativos. [45]
Referencias
- ^ Weisstein, Eric W. "Congruencia". Wolfram MathWorld . Consultado el 27 de agosto de 2020 .
- ^ Caldwell, Chris. "residuo". Glosario de Prime . Consultado el 27 de agosto de 2020 .
- ^ Knuth, Donald. E. (1972). El arte de la programación informática . Addison-Wesley.
- ^ Boute, Raymond T. (abril de 1992). "La definición euclidiana de las funciones div y mod". ACM Transactions on Programming Languages and Systems . 14 (2). ACM Press (Nueva York, NY, EE. UU.): 127–144. doi :10.1145/128861.128862. hdl : 1854/LU-314490 . S2CID 8321674.
- ^ ab Leijen, Daan (3 de diciembre de 2001). "División y módulo para científicos informáticos" (PDF) . Microsoft . Consultado el 25 de diciembre de 2014 .
- ^ Peterson, Doctor (5 de julio de 2001). "Función Mod y números negativos". Foro de Matemáticas - Pregúntele al Dr. Math . Archivado desde el original el 22 de octubre de 2019. Consultado el 22 de octubre de 2019 .
- ^ Horvath, Adam (5 de julio de 2012). "División más rápida y operación módulo: la potencia de dos".
- ^ ab ISO/IEC 8652:2012 - Tecnología de la información — Lenguajes de programación — Ada . ISO , IEC . 2012. sec. 4.5.5 Operadores de multiplicación.
- ^ "Especificación C99 (ISO/IEC 9899:TC2)" (PDF) . 2005-05-06. sec. 6.5.5 Operadores multiplicativos . Consultado el 16 de agosto de 2018 .
- ^ ISO/IEC 14882:2003: Lenguajes de programación – C++ . Organización Internacional de Normalización (ISO), Comisión Electrotécnica Internacional (IEC). 2003. sec. 5.6.4.
el operador binario % produce el resto de la división de la primera expresión por la segunda. .... Si ambos operandos son no negativos, entonces el resto es no negativo; si no, el signo del resto está definido por la implementación
- ^ ISO/IEC 9899:1990: Lenguajes de programación – C . ISO , IEC . 1990. sec. 7.5.6.4.
La
función
fmod devuelve el valor
x - i * y
, para algún entero
i
tal que, si
y
es distinto de cero, el resultado tiene el mismo signo que
x
y una magnitud menor que la magnitud de
y
.
- ^ de dotnet-bot. "Método Math.IEEERemainder(Double, Double) (sistema)". Microsoft Learn . Consultado el 4 de octubre de 2022 .
- ^ "clojure.core - Documentación de la API de Clojure v1.10.3". clojure.github.io . Consultado el 16 de marzo de 2022 .
- ^ "clojure.core - Documentación de la API de Clojure v1.10.3". clojure.github.io . Consultado el 16 de marzo de 2022 .
- ^ ab ISO/IEC JTC 1/SC 22/WG 4 (enero de 2023). ISO/IEC 1989:2023 – Lenguaje de programación COBOL . ISO .
{{cite book}}: CS1 maint: nombres numéricos: lista de autores ( enlace ) - ^ Operadores de CoffeeScript
- ^ ISO/IEC JTC 1/SC 22 (febrero de 2012). ISO/IEC 23271:2012 — Tecnología de la información — Infraestructura de lenguaje común (CLI). ISO . §§ III.3.55–56.
{{cite book}}: CS1 maint: nombres numéricos: lista de autores ( enlace ) - ^ "mod() - CSS: Hojas de estilo en cascada | MDN". developer.mozilla.org . 2024-06-22 . Consultado el 2024-10-23 .
- ^ "rem() - CSS: Hojas de estilo en cascada | MDN". developer.mozilla.org . 2024-10-15 . Consultado el 2024-10-23 .
- ^ "Expresiones - Lenguaje de programación D". dlang.org . Consultado el 1 de junio de 2021 .
- ^ "método operador % - clase num - biblioteca dart:core - API Dart". api.dart.dev . Consultado el 1 de junio de 2021 .
- ^ "método remainder - clase num - biblioteca dart:core - API de Dart". api.dart.dev . Consultado el 1 de junio de 2021 .
- ^ "Kernel — Elixir v1.11.3". hexdocs.pm . Consultado el 28 de enero de 2021 .
- ^ "Integer — Elixir v1.11.3". hexdocs.pm . Consultado el 28 de enero de 2021 .
- ^ "Conceptos básicos: núcleo 1.0.5". package.elm-lang.org . Consultado el 16 de marzo de 2022 .
- ^ "Conceptos básicos: núcleo 1.0.5". package.elm-lang.org . Consultado el 16 de marzo de 2022 .
- ^ "Erlang -- matemáticas". erlang.org . Consultado el 1 de junio de 2021 .
- ^ ANSI (28 de enero de 1987). Lenguajes de programación: BASIC completo. Nueva York: Instituto Nacional Estadounidense de Estándares. § 5.4.4.
X módulo Y, es decir, XY*INT(X/Y).
- ^ ANSI (28 de enero de 1987). Lenguajes de programación: BASIC completo. Nueva York: American National Standards Institute. § 5.4.4.
La función restante, es decir, XY*IP(X/Y).
- ^ "Especificación del lenguaje GLSL, versión 4.50.7" (PDF) . Sección 5.9 Expresiones.
Si ambos operandos son no negativos, entonces el resto es no negativo. Los resultados no están definidos si uno o ambos operandos son negativos.
- ^ "Especificación del lenguaje GLSL, versión 4.50.7" (PDF) . sección 8.3 Funciones comunes.
- ^ "La especificación del lenguaje de programación Go - El lenguaje de programación Go". go.dev . Consultado el 28 de febrero de 2022 .
- ^ "paquete matemático - math - pkg.go.dev". pkg.go.dev . Consultado el 28 de febrero de 2022 .
- ^ "paquete grande - math/big - pkg.go.dev". pkg.go.dev . Consultado el 28 de febrero de 2022 .
- ^ "paquete grande - math/big - pkg.go.dev". pkg.go.dev . Consultado el 12 de abril de 2024 .
- ^ ab "6 tipos y clases predefinidos". www.haskell.org . Consultado el 22 de mayo de 2022 .
- ^ "Operadores". Microsoft . 30 de junio de 2021 . Consultado el 19 de julio de 2021 .
El operador % se define solo en los casos en los que ambos lados son positivos o ambos lados son negativos. A diferencia de C, también opera con tipos de datos de punto flotante, así como con números enteros.
- ^ "Matemáticas · El lenguaje Julia". docs.julialang.org . Consultado el 20 de noviembre de 2021 .
- ^ "Matemáticas · El lenguaje Julia". docs.julialang.org . Consultado el 20 de noviembre de 2021 .
- ^ "rem - Lenguaje de programación Kotlin". Kotlin . Consultado el 5 de mayo de 2021 .
- ^ "mod - Lenguaje de programación Kotlin". Kotlin . Consultado el 5 de mayo de 2021 .
- ^ "Capítulo 3: El lenguaje NASM". NASM - El ensamblador de red versión 2.15.05 .
- ^ "Biblioteca OCaml: Stdlib". ocaml.org . Consultado el 19 de febrero de 2022 .
- ^ "Biblioteca OCaml: Stdlib". ocaml.org . Consultado el 19 de febrero de 2022 .
- ^ Documentación de Perl
- ^ "PHP: Operadores aritméticos - Manual" www.php.net . Consultado el 20 de noviembre de 2021 .
- ^ "PHP: fmod - Manual" www.php.net . Consultado el 20 de noviembre de 2021 .
- ^ "Anillo Euclidiano".
- ^ QuantumWriter. "Expresiones". docs.microsoft.com . Consultado el 11 de julio de 2018 .
- ^ "R: Operadores aritméticos". search.r-project.org . Consultado el 24 de diciembre de 2022 .
- ^ "F32 - Óxido".
- ^ desde r6rs.org
- ^ "Lenguaje de comandos de Shell". pubs.opengroup.org . Consultado el 5 de febrero de 2021 .
- ^ "Documentación de Solidity". docs.soliditylang.org . Consultado el 17 de octubre de 2024 .
- ^ "Documentación para desarrolladores de Apple". developer.apple.com . Consultado el 20 de noviembre de 2021 .
- ^ "Documentación para desarrolladores de Apple". developer.apple.com . Consultado el 20 de noviembre de 2021 .
- ^ "Documentación para desarrolladores de Apple". developer.apple.com . Consultado el 20 de noviembre de 2021 .
- ^ ab Rossberg, Andreas, ed. (19 de abril de 2022). "Especificación básica de WebAssembly: versión 2.0". Consorcio World Wide Web . § 4.3.2 Operaciones con números enteros.
- ^ "Documentación de Zig". Lenguaje de programación Zig . Consultado el 18 de diciembre de 2022 .
- ^ ab "Mod". Centro de documentación de sistemas y lenguajes Wolfram . Wolfram Research . 2020. Consultado el 8 de abril de 2020 .
Enlaces externos
- Diferentes tipos de división de números enteros
- Modulorama, animación de una representación cíclica de las tablas de multiplicar (explicación en francés)