Transformación natural

En la teoría de categorías , una rama de las matemáticas , una transformación natural proporciona una forma de transformar un funtor en otro respetando la estructura interna (es decir, la composición de morfismos ) de las categorías involucradas. Por lo tanto, una transformación natural puede considerarse un "morfismo de funtores". De manera informal, la noción de transformación natural establece que una función particular entre funtores puede realizarse de manera consistente sobre una categoría completa.

De hecho, esta intuición puede formalizarse para definir las llamadas categorías de funtores . Las transformaciones naturales son, después de las categorías y los funtores, una de las nociones más fundamentales de la teoría de categorías y, en consecuencia, aparecen en la mayoría de sus aplicaciones.

Si y son funtores entre las categorías y (ambos de a ), entonces una transformación natural de a es una familia de morfismos que satisface dos requisitos.${\estilo de visualización F}$${\estilo de visualización G}$${\estilo de visualización C}$${\estilo de visualización D}$${\estilo de visualización C}$${\estilo de visualización D}$ ${\estilo de visualización \eta}$${\estilo de visualización F}$${\estilo de visualización G}$

1. La transformación natural debe asociar a cada objeto de , un morfismo entre objetos de . El morfismo se denomina componente de en .${\estilo de visualización X}$${\estilo de visualización C}$ ${\displaystyle \eta_{X}:F(X)\to G(X)}$${\estilo de visualización D}$$estilo de visualización {\eta__{X}}$${\estilo de visualización \eta}$${\estilo de visualización X}$
2. Los componentes deben ser tales que para cada morfismo en tengamos:${\displaystyle f:X\to Y}$${\estilo de visualización C}$

${\displaystyle \eta_{Y}\circ F(f)=G(f)\circ \eta_{X}}$

La última ecuación se puede expresar convenientemente mediante el diagrama conmutativo

Si tanto y son contravariantes , las flechas verticales en el diagrama de la derecha están invertidas. Si es una transformación natural de a , también escribimos o . Esto también se expresa diciendo que la familia de morfismos es natural en .${\estilo de visualización F}$${\estilo de visualización G}$${\estilo de visualización \eta}$${\estilo de visualización F}$${\estilo de visualización G}$${\displaystyle \eta :F\to G}$${\displaystyle \eta :F\Rightarrow G}$${\displaystyle \eta_{X}:F(X)\to G(X)}$${\estilo de visualización X}$

Si, para cada objeto en , el morfismo es un isomorfismo en , entonces se dice que es un${\estilo de visualización X}$${\estilo de visualización C}$$estilo de visualización {\eta__{X}}$${\estilo de visualización D}$${\estilo de visualización \eta}$isomorfismo natural (o a vecesequivalencia naturaloisomorfismo de funtores). Dos funtoresyse denominannaturalmente isomorfoso simplementeisomorfossi existe un isomorfismo natural dea.${\estilo de visualización F}$${\estilo de visualización G}$${\estilo de visualización F}$${\estilo de visualización G}$

Una transformación infranatural de a es simplemente una familia de morfismos , para todos en . Por lo tanto, una transformación natural es una transformación infranatural para la cual para cada morfismo . El naturalizador de , nat , es la subcategoría más grande de que contiene todos los objetos de en que se restringe a una transformación natural.${\estilo de visualización \eta}$${\estilo de visualización F}$${\estilo de visualización G}$${\displaystyle \eta_{X}:F(X)\to G(X)}$${\estilo de visualización X}$${\estilo de visualización C}$${\displaystyle \eta_{Y}\circ F(f)=G(f)\circ \eta_{X}}$${\displaystyle f:X\to Y}$${\estilo de visualización \eta}$${\estilo de visualización (\eta )}$${\estilo de visualización C}$${\estilo de visualización C}$${\estilo de visualización \eta}$

Afirmaciones como

"Todo grupo es naturalmente isomorfo a su grupo opuesto "

abundan en las matemáticas modernas. Ahora daremos el significado preciso de esta afirmación así como su demostración. Consideremos la categoría de todos los grupos con homomorfismos de grupo como morfismos. Si es un grupo, definimos su grupo opuesto de la siguiente manera: es el mismo conjunto que , y la operación está definida por . Todas las multiplicaciones en se "invierten" de esta manera. La formación del grupo opuesto se convierte en un funtor (covariante) de a si definimos para cualquier homomorfismo de grupo . Nótese que es de hecho un homomorfismo de grupo de a :${\displaystyle {\textbf {Grp}}}$${\estilo de visualización (G,*)}$${\displaystyle (G^{\text{op}},{*}^{\text{op}})}$${\displaystyle G^{\text{op}}}$${\estilo de visualización G}$${\displaystyle *^{\text{op}}}$${\displaystyle a*^{\text{op}}b=b*a}$${\displaystyle G^{\text{op}}}$${\displaystyle {\textbf {Grp}}}$${\displaystyle {\textbf {Grp}}}$${\displaystyle f^{\text{op}}=f}$${\displaystyle f:G\to H}$${\displaystyle f^{\text{op}}}$${\displaystyle G^{\text{op}}}$${\displaystyle H^{\text{op}}}$

${\displaystyle f^{\text{op}}(a*^{\text{op}}b)=f(b*a)=f(b)*f(a)=f^{\text{op}}(a)*^{\text{op}}f^{\text{op}}(b).}$

El contenido de la declaración anterior es:

"El funtor identidad es naturalmente isomorfo al funtor opuesto "${\displaystyle {\text{Id}}_{\textbf {Grp}}:{\textbf {Grp}}\to {\textbf {Grp}}}$${\displaystyle {\text{op}}:{\textbf {Grp}}\to {\textbf {Grp}}}$

Para probar esto, necesitamos proporcionar isomorfismos para cada grupo , de modo que el diagrama anterior conmute. Conjunto . Las fórmulas y muestran que es un homomorfismo de grupo con inversa . Para probar la naturalidad, comenzamos con un homomorfismo de grupo y mostramos , es decir para todo en . Esto es cierto ya que y todo homomorfismo de grupo tiene la propiedad .${\displaystyle \eta _{G}:G\to G^{\text{op}}}$${\estilo de visualización G}$${\displaystyle \eta_{G}(a)=a^{-1}}$${\displaystyle (a*b)^{-1}=b^{-1}*a^{-1}=a^{-1}*^{\text{op}}b^{-1}}$${\displaystyle (a^{-1})^{-1}=a}$$estilo de visualización {\eta _{G}}$${\displaystyle \eta _{G^{\text{op}}}}$${\displaystyle f:G\to H}$${\displaystyle \eta_{H}\circ f=f^{\text{op}}\circ \eta_{G}}$${\displaystyle (f(a))^{-1}=f^{\text{op}}(a^{-1})}$${\estilo de visualización a}$${\estilo de visualización G}$${\displaystyle f^{\text{op}}=f}$${\displaystyle (f(a))^{-1}=f(a^{-1})}$

Sea un homomorfismo de módulos derechos. Para cada módulo izquierdo existe una función natural , forma una transformación natural . Para cada módulo derecho existe una función natural definida por , forma una transformación natural .${\displaystyle \varphi :M\longrightarrow M^{\prime }}$${\estilo de visualización R}$${\estilo de visualización N}$${\displaystyle \varphi \otimes N:M\otimes _{R}N\longrightarrow M^{\prime }\otimes _{R}N}$${\displaystyle \eta :M\otimes _{R}-\implies M'\otimes _{R}-}$${\displaystyle N}$${\displaystyle \eta _{N}:{\text{Hom}}_{R}(M',N)\longrightarrow {\text{Hom}}_{R}(M,N)}$${\displaystyle \eta _{N}(f)=f\varphi }$${\displaystyle \eta :{\text{Hom}}_{R}(M',-)\implies {\text{Hom}}_{R}(M,-)}$

Dado un grupo , podemos definir su abelianización . Sea , denotemos la función de proyección sobre las clases laterales de . Este homomorfismo es "natural en ", es decir, define una transformación natural, que ahora comprobamos. Sea un grupo. Para cualquier homomorfismo , tenemos que está contenido en el núcleo de , porque cualquier homomorfismo en un grupo abeliano mata al subgrupo conmutador. Luego, factorizamos como para el homomorfismo único . Esto crea un funtor y una transformación natural, pero no un isomorfismo natural, del funtor identidad a .${\displaystyle G}$ ${\displaystyle G^{\text{ab}}=G/}$ ${\displaystyle [G,G]}$${\displaystyle \pi _{G}:G\to G^{\text{ab}}}$${\displaystyle [G,G]}$${\displaystyle G}$${\displaystyle H}$${\displaystyle f:G\to H}$${\displaystyle [G,G]}$${\displaystyle \pi _{H}\circ f}$${\displaystyle \pi _{H}\circ f}$${\displaystyle G^{\text{ab}}}$${\displaystyle f^{\text{ab}}\circ \pi _{G}=\pi _{H}\circ f}$${\displaystyle f^{\text{ab}}:G^{\text{ab}}\to H^{\text{ab}}}$${\displaystyle {\text{ab}}:{\textbf {Grp}}\to {\textbf {Grp}}}$${\displaystyle \pi }$${\displaystyle {\text{ab}}}$

Los funtores y las transformaciones naturales abundan en la topología algebraica , y los homomorfismos de Hurewicz sirven como ejemplos. Para cualquier espacio topológico puntiagudo y número entero positivo existe un homomorfismo de grupo${\displaystyle (X,x)}$${\displaystyle n}$

${\displaystyle h_{n}\colon \pi _{n}(X,x)\to H_{n}(X)}$

del -ésimo grupo de homotopía de al -ésimo grupo de homología de . Tanto y son funtores de la categoría Top ^* de espacios topológicos puntiagudos a la categoría Grp de grupos, y es una transformación natural de a .${\displaystyle n}$${\displaystyle (X,x)}$${\displaystyle n}$${\displaystyle X}$${\displaystyle \pi _{n}}$${\displaystyle H_{n}}$${\displaystyle h_{n}}$${\displaystyle \pi _{n}}$${\displaystyle H_{n}}$

Dados anillos conmutativos y con un homomorfismo de anillo , los respectivos grupos de matrices invertibles y heredan un homomorfismo que denotamos por , obtenido al aplicar a cada entrada de la matriz. De manera similar, se restringe a un homomorfismo de grupo , donde denota el grupo de unidades de . De hecho, y son funtores de la categoría de anillos conmutativos a . El determinante en el grupo , denotado por , es un homomorfismo de grupo ${\displaystyle R}$${\displaystyle S}$ ${\displaystyle f:R\to S}$ ${\displaystyle n\times n}$${\displaystyle {\text{GL}}_{n}(R)}$${\displaystyle {\text{GL}}_{n}(S)}$${\displaystyle {\text{GL}}_{n}(f)}$${\displaystyle f}$${\displaystyle f}$${\displaystyle f^{*}:R^{*}\to S^{*}}$${\displaystyle R^{*}}$${\displaystyle R}$${\displaystyle {\text{GL}}_{n}}$${\displaystyle *}$${\displaystyle {\textbf {CRing}}}$${\displaystyle {\textbf {Grp}}}$${\displaystyle {\text{GL}}_{n}(R)}$${\displaystyle {\text{det}}_{R}}$

${\displaystyle {\mbox{det}}_{R}\colon {\mbox{GL}}_{n}(R)\to R^{*}}$

lo cual es natural en : porque el determinante está definido por la misma fórmula para cada anillo, se cumple. Esto hace que el determinante sea una transformación natural de a .${\displaystyle R}$${\displaystyle f^{*}\circ {\text{det}}_{R}={\text{det}}_{S}\circ {\text{GL}}_{n}(f)}$${\displaystyle {\text{GL}}_{n}}$${\displaystyle *}$

Por ejemplo, si es un cuerpo , entonces para cada espacio vectorial sobre tenemos una función lineal inyectiva "natural" del espacio vectorial en su doble dual . Estas funciones son "naturales" en el siguiente sentido: la operación doble dual es un funtor, y las funciones son los componentes de una transformación natural del funtor identidad al funtor doble dual.${\displaystyle K}$ ${\displaystyle V}$${\displaystyle K}$ ${\displaystyle V\to V^{**}}$

Para cada grupo abeliano , el conjunto de funciones desde los enteros hasta el conjunto subyacente de forma un grupo abeliano bajo adición puntual. (Aquí está el funtor olvidadizo estándar ). Dado un morfismo , la función dada por la composición por la izquierda con los elementos del primero es en sí misma un homomorfismo de grupos abelianos; de esta manera obtenemos un funtor . El operador de diferencia finita que lleva cada función a es una función de a sí misma, y ​​la colección de tales funciones da una transformación natural .${\displaystyle G}$${\displaystyle {\text{Hom}}_{\textbf {Set}}(\mathbb {Z} ,U(G))}$${\displaystyle G}$${\displaystyle V_{\mathbb {Z} }(G)}$${\displaystyle U}$ ${\displaystyle U:{\textbf {Ab}}\to {\textbf {Set}}}$${\displaystyle {\textbf {Ab}}}$${\displaystyle \varphi :G\to G'}$${\displaystyle V_{\mathbb {Z} }(\varphi ):V_{\mathbb {Z} }(G)\to V_{\mathbb {Z} }(G')}$${\displaystyle \varphi }$${\displaystyle V_{\mathbb {Z} }:{\textbf {Ab}}\to {\textbf {Ab}}}$${\displaystyle \Delta _{G}}$${\displaystyle f:\mathbb {Z} \to U(G)}$${\displaystyle \Delta (f):n\mapsto f(n+1)-f(n)}$${\displaystyle V_{\mathbb {Z} }(G)}$${\displaystyle \Delta }$${\displaystyle \Delta :V_{\mathbb {Z} }\to V_{\mathbb {Z} }}$

Consideremos la categoría${\displaystyle {\textbf {Ab}}}$ de grupos abelianos y homomorfismos de grupos. Para todos los grupos abelianos , y tenemos un isomorfismo de grupo${\displaystyle X}$${\displaystyle Y}$${\displaystyle Z}$

${\displaystyle {\text{Hom}}(X\otimes Y,Z)\to {\text{Hom}}(X,{\text{Hom}}(Y,Z))}$.

Estos isomorfismos son "naturales" en el sentido de que definen una transformación natural entre los dos funtores involucrados . (Aquí "op" es la categoría opuesta de , que no debe confundirse con el funtor de grupo opuesto trivial en  !)${\displaystyle {\textbf {Ab}}^{\text{op}}\times {\textbf {Ab}}^{\text{op}}\times {\textbf {Ab}}\to {\textbf {Ab}}}$${\displaystyle {\textbf {Ab}}}$${\displaystyle {\textbf {Ab}}}$

Esta es formalmente la adjunción tensor-hom y es un ejemplo arquetípico de un par de funtores adjuntos . Las transformaciones naturales surgen con frecuencia junto con los funtores adjuntos y, de hecho, los funtores adjuntos se definen por un cierto isomorfismo natural. Además, cada par de funtores adjuntos viene equipado con dos transformaciones naturales (generalmente no isomorfismos) llamadas unit y counit .

La noción de transformación natural es categórica y establece (de manera informal) que una función particular entre funtores puede realizarse de manera consistente sobre una categoría completa. De manera informal, una función particular (especialmente un isomorfismo) entre objetos individuales (no categorías completas) se denomina "isomorfismo natural", lo que significa implícitamente que en realidad está definida sobre la categoría completa y define una transformación natural de funtores; la formalización de esta intuición fue un factor motivador en el desarrollo de la teoría de categorías.

Por el contrario, una función particular entre objetos particulares puede ser llamada un isomorfismo no natural (o "un isomorfismo que no es natural") si la función no puede extenderse a una transformación natural en toda la categoría. Dado un objeto, un funtor (tomando para simplificar el primer funtor como la identidad) y un isomorfismo, la prueba de no naturalidad se muestra más fácilmente dando un automorfismo que no conmuta con este isomorfismo (por lo que ). Más firmemente, si uno desea probar que y no son naturalmente isomorfos, sin referencia a un isomorfismo particular, esto requiere mostrar que para cualquier isomorfismo , hay alguno con el que no conmuta; en algunos casos, un solo automorfismo funciona para todos los isomorfismos candidatos mientras que en otros casos uno debe mostrar cómo construir uno diferente para cada isomorfismo. Las funciones de la categoría juegan un papel crucial: cualquier transformación infranatural es natural si las únicas funciones son la función identidad, por ejemplo.${\displaystyle X,}$${\displaystyle G}$${\displaystyle \eta \colon X\to G(X),}$${\displaystyle A\colon X\to X}$${\displaystyle \eta \circ A\neq G(A)\circ \eta }$${\displaystyle X}$${\displaystyle G(X)}$${\displaystyle \eta }$${\displaystyle A}$${\displaystyle A}$${\displaystyle \eta }$${\displaystyle A_{\eta }}$

Esto es similar (pero más categórico) a los conceptos de la teoría de grupos o la teoría de módulos, donde una descomposición dada de un objeto en una suma directa "no es natural", o más bien "no es única", ya que existen automorfismos que no preservan la descomposición de la suma directa; véase Teorema de estructura para módulos finitamente generados sobre un dominio ideal principal § Unicidad, por ejemplo.

Algunos autores distinguen notacionalmente, utilizando para un isomorfismo natural y para un isomorfismo no natural, reservando para la igualdad (generalmente igualdad de mapas).${\displaystyle \cong }$${\displaystyle \approx }$${\displaystyle =}$

Como ejemplo de la distinción entre el enunciado funcional y los objetos individuales, considere los grupos de homotopía de un espacio de producto, específicamente el grupo fundamental del toro.

Los grupos de homotopía de un espacio producto son naturalmente el producto de los grupos de homotopía de los componentes, con el isomorfismo dado por la proyección sobre los dos factores, fundamentalmente porque las funciones en un espacio producto son exactamente productos de las funciones en los componentes – esto es una declaración funcional.${\displaystyle \pi _{n}((X,x_{0})\times (Y,y_{0}))\cong \pi _{n}((X,x_{0}))\times \pi _{n}((Y,y_{0})),}$

Sin embargo, el toro (que es en abstracto un producto de dos círculos) tiene un grupo fundamental isomorfo a , pero la división no es natural. Nótese el uso de , , y : ^[a]${\displaystyle Z^{2}}$${\displaystyle \pi _{1}(T,t_{0})\approx \mathbf {Z} \times \mathbf {Z} }$${\displaystyle \approx }$${\displaystyle \cong }$${\displaystyle =}$

${\displaystyle \pi _{1}(T,t_{0})\approx \pi _{1}(S^{1},x_{0})\times \pi _{1}(S^{1},y_{0})\cong \mathbf {Z} \times \mathbf {Z} =\mathbf {Z} ^{2}.}$

Este isomorfismo abstracto con un producto no es natural, ya que algunos isomorfismos de no preservan el producto: el autohomeomorfismo de (considerado como el espacio cociente ) dado por (geométricamente un giro de Dehn sobre una de las curvas generadoras) actúa como esta matriz en (está en el grupo lineal general de matrices enteras invertibles), que no preserva la descomposición como un producto porque no es diagonal. Sin embargo, si se da el toro como un producto -equivalentemente, dada una descomposición del espacio- entonces la división del grupo se sigue de la afirmación general anterior. En términos categóricos, la categoría relevante (preservando la estructura de un espacio de producto) es "mapas de espacios de producto, es decir, un par de mapas entre los componentes respectivos".${\displaystyle T}$${\displaystyle T}$ ${\displaystyle R^{2}/\mathbb {Z} ^{2}}$${\displaystyle \left({\begin{smallmatrix}1&1\\0&1\end{smallmatrix}}\right)}$${\displaystyle \mathbb {Z} ^{2}}$ ${\displaystyle {\text{GL}}(\mathbb {Z} ,2)}$${\displaystyle (T,t_{0})=(S^{1},x_{0})\times (S^{1},y_{0})}$

La naturalidad es una noción categórica y requiere ser muy preciso acerca de exactamente qué datos se dan: el toro como un espacio que resulta ser un producto (en la categoría de espacios y mapas continuos) es diferente del toro presentado como un producto (en la categoría de productos de dos espacios y mapas continuos entre los respectivos componentes).

Todo espacio vectorial de dimensión finita es isomorfo a su espacio dual, pero puede haber muchos isomorfismos diferentes entre los dos espacios. En general, no existe un isomorfismo natural entre un espacio vectorial de dimensión finita y su espacio dual. ^[1] Sin embargo, las categorías relacionadas (con estructura adicional y restricciones en las funciones) sí tienen un isomorfismo natural, como se describe a continuación.

El espacio dual de un espacio vectorial de dimensión finita es a su vez un espacio vectorial de dimensión finita de la misma dimensión, y por lo tanto son isomorfos, ya que la dimensión es el único invariante de los espacios vectoriales de dimensión finita sobre un cuerpo dado. Sin embargo, en ausencia de restricciones adicionales (como un requisito de que las aplicaciones conserven la base elegida), la aplicación de un espacio a su dual no es única, y por lo tanto tal isomorfismo requiere una elección, y "no es natural". En la categoría de espacios vectoriales de dimensión finita y aplicaciones lineales, se puede definir un isomorfismo infranatural de espacios vectoriales a su dual eligiendo un isomorfismo para cada espacio (por ejemplo, eligiendo una base para cada espacio vectorial y tomando el isomorfismo correspondiente), pero esto no definirá una transformación natural. Intuitivamente esto se debe a que requirió una elección, rigurosamente porque cualquier elección de isomorfismos de este tipo no conmutará, por ejemplo, con la aplicación cero; véase (Mac Lane & Birkhoff 1999, §VI.4) para una discusión detallada.

Partiendo de espacios vectoriales de dimensión finita (como objetos) y de los funtores identidad y dual, se puede definir un isomorfismo natural, pero esto requiere primero añadir una estructura adicional, y luego restringir las funciones de "todas las funciones lineales" a "funciones lineales que respetan esta estructura". Explícitamente, para cada espacio vectorial, se requiere que venga con los datos de un isomorfismo a su dual, . En otras palabras, se toman como objetos espacios vectoriales con una forma bilineal no degenerada . Esto define un isomorfismo infranatural (isomorfismo para cada objeto). Luego se restringen las funciones a solo aquellas funciones que conmutan con los isomorfismos: o en otras palabras, se conserva la forma bilineal: . (Estos mapas definen el naturalizador de los isomorfismos.) La categoría resultante, con objetos que son espacios vectoriales de dimensión finita con una forma bilineal no degenerada, y mapas que son transformaciones lineales que respetan la forma bilineal, por construcción tiene un isomorfismo natural de la identidad al dual (cada espacio tiene un isomorfismo con su dual, y se requiere que los mapas en la categoría conmuten). Vista desde esta perspectiva, esta construcción (agregar transformaciones para cada objeto, restringir los mapas para que conmuten con estos) es completamente general, y no depende de ninguna propiedad particular de los espacios vectoriales.${\displaystyle \eta _{V}\colon V\to V^{*}}$ ${\displaystyle b_{V}\colon V\times V\to K}$${\displaystyle T\colon V\to U}$${\displaystyle T^{*}(\eta _{U}(T(v)))=\eta _{V}(v)}$${\displaystyle b_{U}(T(v),T(w))=b_{V}(v,w)}$

En esta categoría (espacios vectoriales de dimensión finita con una forma bilineal no degenerada, aplicaciones, transformaciones lineales que respetan la forma bilineal), el dual de una aplicación entre espacios vectoriales puede identificarse como una transpuesta . A menudo, por razones de interés geométrico, esto se especializa en una subcategoría, al requerir que las formas bilineales no degeneradas tengan propiedades adicionales, como ser simétricas ( matrices ortogonales ), simétricas y definidas positivas ( espacio de producto interno ), simétricas sesquilineales ( espacios hermíticos ), antisimétricas y totalmente isótropas ( espacio vectorial simpléctico ), etc. – en todas estas categorías, un espacio vectorial se identifica naturalmente con su dual, por la forma bilineal no degenerada.

Si y son transformaciones naturales entre funtores , entonces podemos componerlos para obtener una transformación natural . Esto se hace por componentes:${\displaystyle \eta :F\Rightarrow G}$${\displaystyle \epsilon :G\Rightarrow H}$${\displaystyle F,G,H:C\to D}$${\displaystyle \epsilon \circ \eta :F\Rightarrow H}$

${\displaystyle (\epsilon \circ \eta )_{X}=\epsilon _{X}\circ \eta _{X}}$.

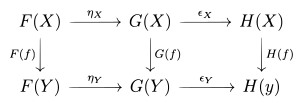
Esta composición vertical de transformaciones naturales es asociativa y tiene una identidad, y permite considerar la colección de todos los funtores como una categoría (ver más abajo Categorías de funtores). La transformación natural identidad sobre funtores tiene componentes . ^[2]${\displaystyle C\to D}$${\displaystyle \mathrm {id} _{F}}$${\displaystyle F}$${\displaystyle (\mathrm {id} _{F})_{X}=\mathrm {id} _{F(X)}}$

Para , .${\displaystyle \eta :F\Rightarrow G}$${\displaystyle \mathrm {id} _{G}\circ \eta =\eta =\eta \circ \mathrm {id} _{F}}$

Si es una transformación natural entre funtores y es una transformación natural entre funtores , entonces la composición de funtores permite una composición de transformaciones naturales con componentes${\displaystyle \eta :F\Rightarrow G}$${\displaystyle F,G:C\to D}$${\displaystyle \epsilon :J\Rightarrow K}$${\displaystyle J,K:D\to E}$${\displaystyle \epsilon *\eta :J\circ F\Rightarrow K\circ G}$

${\displaystyle (\epsilon *\eta )_{X}=\epsilon _{G(X)}\circ J(\eta _{X})=K(\eta _{X})\circ \epsilon _{F(X)}}$.

Al utilizar whiskering (ver más abajo), podemos escribir

${\displaystyle (\epsilon *\eta )_{X}=(\epsilon G)_{X}\circ (J\eta )_{X}=(K\eta )_{X}\circ (\epsilon F)_{X}}$,

por eso

${\displaystyle \epsilon *\eta =\epsilon G\circ J\eta =K\eta \circ \epsilon F}$.

Esta composición horizontal de transformaciones naturales es también asociativa con identidad. Esta identidad es la transformación natural identidad sobre el funtor identidad , es decir, la transformación natural que asocia a cada objeto su morfismo identidad : para objeto en categoría , .${\displaystyle X}$${\displaystyle C}$${\displaystyle (\mathrm {id} _{\mathrm {id} _{C}})_{X}=\mathrm {id} _{\mathrm {id} _{C}(X)}=\mathrm {id} _{X}}$

Para con , .${\displaystyle \eta :F\Rightarrow G}$${\displaystyle F,G:C\to D}$${\displaystyle \mathrm {id} _{\mathrm {id} _{D}}*\eta =\eta =\eta *\mathrm {id} _{\mathrm {id} _{C}}}$

Como los funtores identidad y son funtores, la identidad para la composición horizontal es también la identidad para la composición vertical, pero no al revés. ^[3]${\displaystyle \mathrm {id} _{C}}$${\displaystyle \mathrm {id} _{D}}$

Whiskering es una operación binaria externa entre un funtor y una transformación natural. ^{[4] [5]}

Si es una transformación natural entre funtores , y es otro funtor, entonces podemos formar la transformación natural definiendo${\displaystyle \eta :F\Rightarrow G}$${\displaystyle F,G:C\to D}$${\displaystyle H:D\to E}$${\displaystyle H\eta :H\circ F\Rightarrow H\circ G}$

${\displaystyle (H\eta )_{X}=H(\eta _{X})}$.

Si por el contrario es un funtor, la transformación natural se define por${\displaystyle K:B\to C}$${\displaystyle \eta K:F\circ K\Rightarrow G\circ K}$

${\displaystyle (\eta K)_{X}=\eta _{K(X)}}$.

También es una composición horizontal donde una de las transformaciones naturales es la transformación natural de la identidad:

${\displaystyle H\eta =\mathrm {id} _{H}*\eta }$y .${\displaystyle \eta K=\eta *\mathrm {id} _{K}}$

Nótese que (resp. ) generalmente no es la identidad izquierda (resp. derecha) de la composición horizontal ( y en general), excepto si (resp. ) es el funtor identidad de la categoría (resp. ).${\displaystyle \mathrm {id} _{H}}$${\displaystyle \mathrm {id} _{K}}$${\displaystyle *}$${\displaystyle H\eta \neq \eta }$${\displaystyle \eta K\neq \eta }$${\displaystyle H}$${\displaystyle K}$${\displaystyle D}$${\displaystyle C}$

Las dos operaciones están relacionadas por una identidad que intercambia la composición vertical con la composición horizontal: si tenemos cuatro transformaciones naturales como las que se muestran en la imagen de la derecha, entonces se cumple la siguiente identidad:${\displaystyle \alpha ,\alpha ',\beta ,\beta '}$

${\displaystyle (\beta '\circ \alpha ')*(\beta \circ \alpha )=(\beta '*\beta )\circ (\alpha '*\alpha )}$.

Las composiciones verticales y horizontales también se vinculan a través de transformaciones naturales de identidad:

para y , . ^[6]${\displaystyle F:C\to D}$${\displaystyle G:D\to E}$${\displaystyle \mathrm {id} _{G}*\mathrm {id} _{F}=\mathrm {id} _{G\circ F}}$

Como el whiskering es una composición horizontal con una identidad, la ley de intercambio da inmediatamente las fórmulas compactas de composición horizontal de y sin tener que analizar componentes y el diagrama conmutativo:${\displaystyle \eta :F\Rightarrow G}$${\displaystyle \epsilon :J\Rightarrow K}$

${\displaystyle {\begin{aligned}\epsilon *\eta &=(\epsilon \circ \mathrm {id} _{J})*(\mathrm {id} _{G}\circ \eta )=(\epsilon *\mathrm {id} _{G})\circ (\mathrm {id} _{J}*\eta )=\epsilon G\circ J\eta \\&=(\mathrm {id} _{K}\circ \epsilon )*(\eta \circ \mathrm {id} _{F})=(\mathrm {id} _{K}*\eta )\circ (\epsilon *\mathrm {id} _{F})=K\eta \circ \epsilon F\end{aligned}}}$.

Si es cualquier categoría y es una categoría pequeña , podemos formar la categoría de funtores teniendo como objetos todos los funtores desde a y como morfismos las transformaciones naturales entre esos funtores. Esto forma una categoría ya que para cualquier funtor hay una transformación natural identidad (que asigna a cada objeto el morfismo identidad en ) y la composición de dos transformaciones naturales (la "composición vertical" anterior) es nuevamente una transformación natural.${\displaystyle C}$${\displaystyle I}$ ${\displaystyle C^{I}}$${\displaystyle I}$${\displaystyle C}$${\displaystyle F}$${\displaystyle 1_{F}:F\to F}$${\displaystyle X}$${\displaystyle F(X)}$

Los isomorfismos en son precisamente los isomorfismos naturales. Es decir, una transformación natural es un isomorfismo natural si y sólo si existe una transformación natural tal que y .${\displaystyle C^{I}}$${\displaystyle \eta :F\to G}$${\displaystyle \epsilon :G\to F}$${\displaystyle \eta \epsilon =1_{G}}$${\displaystyle \epsilon \eta =1_{F}}$

La categoría de functor es especialmente útil si surge de un grafo dirigido . Por ejemplo, si es la categoría del grafo dirigido • → • , entonces tiene como objetos los morfismos de , y un morfismo entre y en es un par de morfismos y en tal que el "cuadrado conmuta", es decir .${\displaystyle C^{I}}$${\displaystyle I}$${\displaystyle I}$${\displaystyle C^{I}}$${\displaystyle C}$${\displaystyle \phi :U\to V}$${\displaystyle \psi :X\to Y}$${\displaystyle C^{I}}$${\displaystyle f:U\to X}$${\displaystyle g:V\to Y}$${\displaystyle C}$${\displaystyle \psi \circ f=g\circ \phi }$

De manera más general, se puede construir la categoría 2 cuya${\displaystyle {\textbf {Cat}}}$

• Las celdas 0 (objetos) son las categorías pequeñas,
• 1-celdas (flechas) entre dos objetos y son los funtores de a ,${\displaystyle C}$${\displaystyle D}$${\displaystyle C}$${\displaystyle D}$
• 2-celdas entre dos 1-celdas (functores) y son las transformaciones naturales de a .${\displaystyle F:C\to D}$${\displaystyle G:C\to D}$${\displaystyle F}$${\displaystyle G}$

Las composiciones horizontales y verticales son las composiciones entre las transformaciones naturales descritas anteriormente. Una categoría de functor es entonces simplemente una categoría hom en esta categoría (cuestiones de pequeñez aparte).${\displaystyle C^{I}}$

Cada límite y colímite proporciona un ejemplo de transformación natural simple, ya que un cono equivale a una transformación natural con el funtor diagonal como dominio. De hecho, si los límites y colímites se definen directamente en términos de su propiedad universal , son morfismos universales en una categoría de funtores.

Si es un objeto de una categoría localmente pequeña , entonces la asignación define un funtor covariante . Este funtor se llama representable (de manera más general, un funtor representable es cualquier funtor naturalmente isomorfo a este funtor para una elección apropiada de ). Las transformaciones naturales de un funtor representable a un funtor arbitrario son completamente conocidas y fáciles de describir; este es el contenido del lema de Yoneda .${\displaystyle X}$ ${\displaystyle C}$${\displaystyle Y\mapsto {\text{Hom}}_{C}(X,Y)}$${\displaystyle F_{X}:C\to {\textbf {Set}}}$${\displaystyle X}$${\displaystyle F:C\to {\textbf {Set}}}$

Se dice que Saunders Mac Lane , uno de los fundadores de la teoría de categorías, comentó: "No inventé categorías para estudiar funtores; las inventé para estudiar transformaciones naturales". ^[7] Así como el estudio de los grupos no está completo sin un estudio de los homomorfismos , el estudio de las categorías no está completo sin el estudio de los funtores . La razón del comentario de Mac Lane es que el estudio de los funtores en sí mismo no está completo sin el estudio de las transformaciones naturales.

El contexto de la observación de Mac Lane fue la teoría axiomática de la homología . Se podía demostrar que diferentes formas de construir la homología coincidían: por ejemplo, en el caso de un complejo simplicial, los grupos definidos directamente serían isomorfos a los de la teoría singular. Lo que no se puede expresar fácilmente sin el lenguaje de las transformaciones naturales es cómo los grupos de homología son compatibles con los morfismos entre objetos, y cómo dos teorías de homología equivalentes no sólo tienen los mismos grupos de homología, sino también los mismos morfismos entre esos grupos.

• Transformación extranatural
• Propiedad universal
• Teoría de categorías superiores

• nLab, un proyecto wiki sobre matemáticas, física y filosofía con énfasis en el punto de vista n -categórico
• J. Adamek, H. Herrlich, G. Strecker, Categorías abstractas y concretas: la alegría de los gatos
• Enciclopedia de filosofía de Stanford : "Teoría de categorías", de Jean-Pierre Marquis. Bibliografía extensa.
• Baez, John, 1996, "La historia de las n-categorías". Una introducción informal a las categorías superiores.