Transición vítrea

La transición vidrio-líquido , o transición vítrea , es la transición gradual y reversible en materiales amorfos (o en regiones amorfas dentro de materiales semicristalinos ) de un estado "vítreo" duro y relativamente frágil a un estado viscoso o gomoso a medida que aumenta la temperatura. [2] Un sólido amorfo que exhibe una transición vítrea se llama vidrio . La transición inversa, lograda al sobreenfriar un líquido viscoso al estado vítreo, se llama vitrificación .
La temperatura de transición vítrea T g de un material caracteriza el rango de temperaturas en el que se produce esta transición vítrea (como definición experimental, típicamente marcada como 100 s de tiempo de relajación). Siempre es menor que la temperatura de fusión , T m , del estado cristalino del material, si existe, porque el vidrio es un estado de energía más alto (o entalpía a presión constante) que el cristal correspondiente.
Los plásticos duros como el poliestireno y el poli(metacrilato de metilo) se utilizan muy por debajo de sus temperaturas de transición vítrea, es decir, cuando están en su estado vítreo. Sus valores de T g están en torno a los 100 °C (212 °F). Los elastómeros de caucho como el poliisopreno y el poliisobutileno se utilizan por encima de su T g , es decir, en el estado gomoso, donde son blandos y flexibles; la reticulación impide el flujo libre de sus moléculas, lo que confiere al caucho una forma fija a temperatura ambiente (a diferencia de un líquido viscoso). [3]
A pesar del cambio en las propiedades físicas de un material a través de su transición vítrea, la transición no se considera una transición de fase ; más bien es un fenómeno que se extiende sobre un rango de temperatura y se define por una de varias convenciones. [4] [5] Tales convenciones incluyen una velocidad de enfriamiento constante (20 kelvins por minuto (36 °F/min)) [2] y un umbral de viscosidad de 10 12 Pa·s , entre otros. Al enfriarse o calentarse a través de este rango de transición vítrea, el material también exhibe un paso suave en el coeficiente de expansión térmica y en el calor específico , y la ubicación de estos efectos nuevamente depende de la historia del material. [6] La cuestión de si alguna transición de fase subyace a la transición vítrea es un tema de investigación en curso. [4] [5] [7] [ ¿cuándo? ]
Transición vítrea (en ciencia de polímeros): proceso en el cual un polímero fundido cambia al enfriarse a un vidrio polimérico o un vidrio polimérico cambia al calentarse a un polímero fundido. [8]
- Los fenómenos que se producen en la transición vítrea de los polímeros siguen siendo objeto de investigación y debate científicos en curso. La transición vítrea presenta características de una transición de segundo orden, ya que los estudios térmicos a menudo indican que las energías de Gibbs molares, las entalpías molares y los volúmenes molares de las dos fases, es decir, la masa fundida y el vidrio, son iguales, mientras que la capacidad térmica y la expansividad son discontinuas. Sin embargo, la transición vítrea generalmente no se considera una transición termodinámica en vista de la dificultad inherente de alcanzar el equilibrio en un vidrio polimérico o en una masa fundida de polímero a temperaturas cercanas a la temperatura de transición vítrea.
- En el caso de los polímeros, los cambios conformacionales de los segmentos, que normalmente constan de entre 10 y 20 átomos en la cadena principal, se vuelven infinitamente lentos por debajo de la temperatura de transición vítrea.
- En un polímero parcialmente cristalino, la transición vítrea ocurre solo en las partes amorfas del material.
- La definición es diferente a la de la referencia [9] .
- No se recomienda el término comúnmente utilizado “transición vidrio-caucho” para la transición vítrea. [8]
Características
La transición vítrea de un líquido a un estado sólido puede ocurrir con enfriamiento o compresión. [10] La transición comprende un aumento suave en la viscosidad de un material de hasta 17 órdenes de magnitud dentro de un rango de temperatura de 500 K sin ningún cambio pronunciado en la estructura del material. [11] Esta transición contrasta con la transición de congelación o cristalización , que es una transición de fase de primer orden en la clasificación de Ehrenfest e implica discontinuidades en las propiedades termodinámicas y dinámicas como el volumen, la energía y la viscosidad. En muchos materiales que normalmente experimentan una transición de congelación, el enfriamiento rápido evitará esta transición de fase y, en su lugar, dará como resultado una transición vítrea a una temperatura más baja. Otros materiales, como muchos polímeros , carecen de un estado cristalino bien definido y forman fácilmente vidrios, incluso con un enfriamiento o compresión muy lentos. La tendencia de un material a formar un vidrio mientras se enfría se llama capacidad de formación de vidrio. Esta capacidad depende de la composición del material y puede predecirse mediante la teoría de la rigidez . [12]
Por debajo del rango de temperatura de transición, la estructura vítrea no se relaja de acuerdo con la velocidad de enfriamiento utilizada. El coeficiente de expansión para el estado vítreo es aproximadamente equivalente al del sólido cristalino. Si se utilizan velocidades de enfriamiento más lentas, el aumento del tiempo para que se produzca la relajación estructural (o reordenamiento intermolecular) puede dar como resultado un producto de vidrio de mayor densidad. De manera similar, mediante el recocido (y permitiendo así una relajación estructural lenta), la estructura del vidrio se acerca con el tiempo a una densidad de equilibrio correspondiente al líquido superenfriado a esta misma temperatura. T g se encuentra en la intersección entre la curva de enfriamiento (volumen versus temperatura) para el estado vítreo y el líquido superenfriado. [13] [14] [15] [16] [17]
La configuración del vidrio en este rango de temperaturas cambia lentamente con el tiempo hacia la estructura de equilibrio. El principio de minimización de la energía libre de Gibbs proporciona la fuerza impulsora termodinámica necesaria para el cambio final. A temperaturas algo más altas que T g , la estructura correspondiente al equilibrio a cualquier temperatura se alcanza con bastante rapidez. En cambio, a temperaturas considerablemente más bajas, la configuración del vidrio permanece sensiblemente estable durante períodos de tiempo cada vez más largos.
Por lo tanto, la transición de líquido a vidrio no es una transición entre estados de equilibrio termodinámico . Se cree ampliamente que el verdadero estado de equilibrio es siempre cristalino. Se cree que el vidrio existe en un estado cinético bloqueado, y su entropía, densidad, etc., dependen de la historia térmica. Por lo tanto, la transición vítrea es principalmente un fenómeno dinámico. El tiempo y la temperatura son cantidades intercambiables (hasta cierto punto) cuando se trata de vidrios, un hecho que a menudo se expresa en el principio de superposición tiempo-temperatura . Al enfriar un líquido, los grados de libertad internos caen sucesivamente fuera del equilibrio . Sin embargo, existe un debate de larga data sobre si existe una transición de fase de segundo orden subyacente en el límite hipotético de tiempos de relajación infinitamente largos. [ aclaración necesaria ] [6] [18] [19] [20]
En un modelo más reciente de transición vítrea, la temperatura de transición vítrea corresponde a la temperatura a la que las aberturas más grandes entre los elementos vibrantes en la matriz líquida se hacen más pequeñas que las secciones transversales más pequeñas de los elementos o partes de ellos cuando la temperatura está disminuyendo. Como resultado de la entrada fluctuante de energía térmica en la matriz líquida, los armónicos de las oscilaciones se alteran constantemente y se crean cavidades temporales ("volumen libre") entre los elementos, cuyo número y tamaño dependen de la temperatura. La temperatura de transición vítrea T g0 definida de esta manera es una constante material fija del estado desordenado (no cristalino) que depende solo de la presión. Como resultado de la inercia creciente de la matriz molecular al acercarse a T g0 , el ajuste del equilibrio térmico se retrasa sucesivamente, de modo que los métodos de medición habituales para determinar la temperatura de transición vítrea en principio proporcionan valores T g que son demasiado altos. En principio, cuanto más lenta sea la velocidad de cambio de temperatura durante la medición, más se acercará el valor T g medido a T g0 . [21] Se pueden utilizar técnicas como el análisis mecánico dinámico para medir la temperatura de transición vítrea. [22]
Definiciones formales
La definición de vidrio y de transición vítrea no está establecida y se han propuesto muchas definiciones durante el siglo pasado. [23]
Franz Simon : [24] El vidrio es un material rígido que se obtiene al congelar un líquido superenfriado en un rango estrecho de temperaturas.
Zachariasen : [25] El vidrio es una red topológicamente desordenada, con un orden de corto alcance equivalente al del cristal correspondiente. [26]
El vidrio es un “líquido congelado” (es decir, líquidos en los que se ha roto la ergodicidad) que, tras un tiempo suficientemente largo, se relaja espontáneamente hacia el estado líquido superenfriado.
Los vidrios son sólidos amorfos estabilizados cinéticamente y termodinámicamente no equilibrados, en los que el desorden molecular y las propiedades termodinámicas correspondientes al estado de la respectiva masa fundida subenfriada a una temperatura T* están congelados. Por lo tanto, T* difiere de la temperatura real T . [27]
El vidrio es un estado condensado de materia no cristalino y sin equilibrio que presenta una transición vítrea. La estructura de los vidrios es similar a la de sus líquidos superenfriados (SCL) originales, y se relajan espontáneamente hacia el estado SCL. Su destino final es solidificarse, es decir, cristalizarse. [23]
Temperatura de transiciónyogramo
Esta sección necesita citas adicionales para su verificación . ( Julio de 2009 ) |


Consulte la figura de la parte inferior derecha que representa gráficamente la capacidad calorífica en función de la temperatura. En este contexto, T g es la temperatura correspondiente al punto A de la curva. [28]
Existen distintas definiciones operativas de la temperatura de transición vítrea T g y varias de ellas se consideran estándares científicos aceptados. Sin embargo, todas las definiciones son arbitrarias y todas arrojan resultados numéricos diferentes: en el mejor de los casos, los valores de T g para una sustancia dada concuerdan en unos pocos grados kelvin. Una definición se refiere a la viscosidad , fijando T g en un valor de 10 13 poise (o 10 12 Pa·s). Como se evidencia experimentalmente, este valor está cerca del punto de recocido de muchos vidrios. [29]
A diferencia de la viscosidad, la expansión térmica , la capacidad calorífica , el módulo de corte y muchas otras propiedades de los vidrios inorgánicos muestran un cambio relativamente repentino en la temperatura de transición vítrea. Cualquier paso o curvatura de este tipo se puede utilizar para definir T g . Para que esta definición sea reproducible, se debe especificar la velocidad de enfriamiento o calentamiento.
La definición de T g que se utiliza con más frecuencia utiliza la energía liberada al calentarse en calorimetría diferencial de barrido (DSC, véase la figura). Normalmente, la muestra se enfría primero a 10 K/min y luego se calienta a esa misma velocidad.
Otra definición de T g utiliza el punto de inflexión en dilatometría (también conocido como expansión térmica): consulte la figura de la parte superior derecha. Aquí, las tasas de calentamiento de 3 a 5 K/min (5,4 a 9,0 °F/min) son comunes. Las secciones lineales por debajo y por encima de T g están coloreadas en verde. T g es la temperatura en la intersección de las líneas de regresión rojas. [28]
A continuación se resumen los valores de T g característicos de ciertas clases de materiales.
Polímeros
| Material | Tg ( ° C) | Tg (°F ) | Nombre comercial |
|---|---|---|---|
| Caucho de neumático | -70 | −94 [30] | |
| Fluoruro de polivinilideno (PVDF) | -35 | −31 [31] | |
| Polipropileno (PP atáctico) | -20 | −4 [32] | |
| Fluoruro de polivinilo (PVF) | -20 | −4 [31] | |
| Polipropileno (PP isotáctico) | 0 | 32 [32] | |
| Poli-3-hidroxibutirato (PHB) | 15 | 59 [32] | |
| Acetato de polivinilo (PVAc) | 30 | 86 [32] | |
| Policlorotrifluoroetileno (PCTFE) | 45 | 113 [31] | |
| Poliamida (PA) | 47–60 | 117–140 | Nailon-6,x |
| Ácido poliláctico (PLA) | 60–65 | 140–149 | |
| Tereftalato de polietileno (PET) | 70 | 158 [32] | |
| Cloruro de polivinilo (PVC) | 80 | 176 [32] | |
| Alcohol polivinílico (PVA) | 85 | 185 [32] | |
| Poliestireno (PS) | 95 | 203 [32] | |
| Poli(metacrilato de metilo) (PMMA atáctico) | 105 | 221 [32] | Plexiglás, Perspex |
| Acrilonitrilo butadieno estireno (ABS) | 105 | 221 [33] | |
| Politetrafluoroetileno (PTFE) | 115 | 239 [34] | Teflón |
| Policarbonato (PC) | 145 | 293 [32] | Lexano |
| Polisulfona | 185 | 365 | |
| Polinorborneno | 215 | 419 [32] |
El nailon-6 seco tiene una temperatura de transición vítrea de 47 °C (117 °F). [35] El nailon-6,6 en estado seco tiene una temperatura de transición vítrea de aproximadamente 70 °C (158 °F). [36] [37] Mientras que el polietileno tiene un rango de transición vítrea de −130 a −80 °C (−202 a −112 °F) [38] Los anteriores son solo valores medios, ya que la temperatura de transición vítrea depende de la velocidad de enfriamiento y la distribución del peso molecular y podría verse influenciada por aditivos. Para un material semicristalino, como el polietileno que es 60–80% cristalino a temperatura ambiente, la transición vítrea citada se refiere a lo que le sucede a la parte amorfa del material al enfriarse.
Silicatos y otros vidrios de red covalente
| Material | Tg ( ° C) | Tg (°F ) |
|---|---|---|
| Calcogenuro GeSbTe | 150 | 302 [39] |
| Calcogenuro AsGeSeTe | 245 | 473 |
| Vidrio fluorado ZBLAN | 235 | 455 |
| Dióxido de telurio | 280 | 536 |
| Fluoroaluminato | 400 | 752 |
| Vidrio sódico-cálcico | 520–600 | 968–1.112 |
| Cuarzo fundido (aproximado) | 1.200 | 2.200 [40] |
Capacidad calorífica lineal

En 1971, Zeller y Pohl descubrieron que [42] cuando el vidrio está a una temperatura muy baja ~1K, su calor específico tiene un componente lineal: . Este es un efecto inusual, porque el material cristalino normalmente tiene , como en el modelo de Debye . Esto se explicó por la hipótesis del sistema de dos niveles, [43] que establece que un vidrio está poblado por sistemas de dos niveles, que parecen un pozo de potencial doble separado por una pared. La pared es lo suficientemente alta como para que no se produzca tunelización por resonancia, pero sí se produce tunelización térmica. Es decir, si los dos pozos tienen una diferencia de energía , entonces una partícula en un pozo puede hacer un túnel hacia el otro pozo por interacción térmica con el entorno. Ahora, imaginemos que hay muchos sistemas de dos niveles en el vidrio, y que su distribución es aleatoria pero fija ("desorden extinguido"), entonces a medida que la temperatura baja, cada vez más de estos niveles de dos niveles se congelan (lo que significa que lleva tanto tiempo que se produzca una tunelización que no se pueden observar experimentalmente).
Consideremos un único sistema de dos niveles que no está congelado, cuya brecha de energía es . Está en una distribución de Boltzmann, por lo que su energía media es .
Ahora, supongamos que los sistemas de dos niveles están todos enfriados, de modo que cada uno varía poco con la temperatura. En ese caso, podemos escribir como la densidad de estados con brecha de energía . También suponemos que es positiva y uniforme cerca de .
Entonces, la energía total aportada por esos sistemas de dos niveles es
El efecto es que la energía promedio en estos sistemas de dos niveles es , lo que conduce a un término.
Datos experimentales
En las mediciones experimentales, se mide la capacidad calorífica específica del vidrio a diferentes temperaturas y se traza un gráfico. Suponiendo que , el gráfico debería mostrar , es decir, una línea recta con pendiente que muestra la capacidad calorífica típica de tipo Debye y una intersección vertical que muestra el componente lineal anómalo. [41]
La paradoja de Kauzmann

A medida que un líquido se enfría demasiado, la diferencia de entropía entre la fase líquida y la sólida disminuye. Al extrapolar la capacidad térmica del líquido enfriado demasiado por debajo de su temperatura de transición vítrea , es posible calcular la temperatura a la que la diferencia de entropías se vuelve cero. Esta temperatura se ha denominado temperatura de Kauzmann .
Si un líquido pudiera ser sobreenfriado por debajo de su temperatura de Kauzmann y efectivamente mostrara una entropía menor que la fase cristalina, esto sería paradójico, ya que la fase líquida debería tener la misma entropía vibracional, pero una entropía posicional mucho mayor, que la fase cristalina. Esta es la paradoja de Kauzmann , aún no resuelta definitivamente. [44] [45]
Posibles resoluciones
Hay muchas soluciones posibles para la paradoja de Kauzmann.
El propio Kauzmann resolvió la paradoja de la entropía postulando que todos los líquidos superenfriados deben cristalizar antes de que se alcance la temperatura de Kauzmann.
Tal vez a la temperatura de Kauzmann, el vidrio alcanza una fase vítrea ideal , que sigue siendo amorfa, pero tiene un orden amorfo de largo alcance que disminuye su entropía total a la del cristal. El vidrio ideal sería una verdadera fase de la materia. [45] [46] Se plantea la hipótesis del vidrio ideal, pero no se puede observar de forma natural, ya que tardaría demasiado en formarse. Se ha observado algo que se acerca a un vidrio ideal como "vidrio ultraestable" formado por deposición de vapor , [47]
Tal vez deba haber una transición de fase antes de que la entropía del líquido disminuya. En este escenario, la temperatura de transición se conoce como temperatura de transición vítrea ideal calorimétrica T 0c . Desde este punto de vista, la transición vítrea no es simplemente un efecto cinético , es decir, simplemente el resultado del enfriamiento rápido de una masa fundida, sino que existe una base termodinámica subyacente para la formación del vidrio. La temperatura de transición vítrea:
Quizás la capacidad térmica del líquido superenfriado cerca de la temperatura de Kauzmann disminuye suavemente hasta un valor más pequeño.
Quizás la transición de fase de primer orden a otro estado líquido ocurre antes de la temperatura de Kauzmann y la capacidad calorífica de este nuevo estado es menor que la obtenida por extrapolación a partir de una temperatura más alta.
En materiales específicos
Sílice, SiO2
La sílice (el compuesto químico SiO 2 ) tiene varias formas cristalinas distintas además de la estructura de cuarzo. Casi todas las formas cristalinas involucran unidades tetraédricas de SiO 4 unidas entre sí por vértices compartidos en diferentes disposiciones ( la stishovita , compuesta de octaedros de SiO 6 unidos , es la principal excepción). Las longitudes de enlace Si-O varían entre las diferentes formas cristalinas. Por ejemplo, en el α-cuarzo la longitud de enlace es de 161 picómetros (6,3 × 10 −9 pulgadas), mientras que en la α-tridimita varía de 154 a 171 pm (6,1 × 10 −9 –6,7 × 10 −9 pulgadas). El ángulo de enlace Si-O-Si también varía de 140° en la α-tridimita a 144° en el α-cuarzo a 180° en la β-tridimita. Cualquier desviación de estos parámetros estándar constituye diferencias o variaciones microestructurales que representan una aproximación a un sólido amorfo , vítreo o vítreo . La temperatura de transición T g en silicatos está relacionada con la energía requerida para romper y volver a formar enlaces covalentes en una red amorfa (o de red aleatoria) de enlaces covalentes . La T g está claramente influenciada por la química del vidrio. Por ejemplo, la adición de elementos como B , Na , K o Ca a un vidrio de sílice , que tienen una valencia menor de 4, ayuda a romper la estructura de la red, reduciendo así la T g . Alternativamente, P , que tiene una valencia de 5, ayuda a reforzar una red ordenada y, por lo tanto, aumenta la T g . [48] T g es directamente proporcional a la fuerza del enlace, es decir, depende de los parámetros termodinámicos de cuasi-equilibrio de los enlaces, por ejemplo, de la entalpía H d y la entropía S d de las configuraciones – enlaces rotos: T g = H d / [ S d + R ln[(1 − f c )/ f c ] donde R es la constante de los gases y f c es el umbral de percolación. Para fundidos fuertes como Si O 2 el umbral de percolación en la ecuación anterior es la densidad crítica universal de Scher-Zallen en el espacio 3-D, por ejemplo, f c= 0,15, sin embargo, para materiales frágiles los umbrales de percolación dependen del material y f c ≪ 1. [49] La entalpía H d y la entropía S d de las configuraciones – enlaces rotos se pueden encontrar a partir de los datos experimentales disponibles sobre viscosidad. [50] En la superficie de películas de SiO 2 , la microscopía de efecto túnel de barrido ha resuelto cúmulos de ca. 5 SiO 2 de diámetro que se mueven en forma de dos estados en una escala de tiempo de minutos. Esto es mucho más rápido que la dinámica en masa, pero de acuerdo con los modelos que comparan la dinámica en masa y la de superficie. [51] [52]
Polímeros
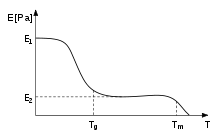
En los polímeros, la temperatura de transición vítrea, T g , se expresa a menudo como la temperatura a la que la energía libre de Gibbs es tal que se excede la energía de activación para el movimiento cooperativo de aproximadamente 50 elementos del polímero [ cita requerida ] . Esto permite que las cadenas moleculares se deslicen unas sobre otras cuando se aplica una fuerza. A partir de esta definición, podemos ver que la introducción de grupos químicos relativamente rígidos (como anillos de benceno ) interferirá con el proceso de flujo y, por lo tanto, aumentará T g . [53] La rigidez de los termoplásticos disminuye debido a este efecto (ver figura). Cuando se ha alcanzado la temperatura vítrea, la rigidez permanece igual durante un tiempo, es decir, en o cerca de E 2 , hasta que la temperatura excede T m , y el material se funde. Esta región se llama meseta de caucho.

En el planchado , se calienta un tejido a través de esta transición de modo que las cadenas de polímero se vuelven móviles. El peso del hierro impone entonces una orientación preferida. La T g se puede reducir significativamente mediante la adición de plastificantes a la matriz de polímero. Las moléculas más pequeñas de plastificante se incrustan entre las cadenas de polímero, aumentando el espaciado y el volumen libre, y permitiéndoles moverse una sobre otra incluso a temperaturas más bajas. La adición de plastificante puede tomar efectivamente el control sobre la dinámica de la cadena de polímero y dominar las cantidades del volumen libre asociado de modo que la mayor movilidad de los extremos del polímero no sea evidente. [54] La adición de grupos laterales no reactivos a un polímero también puede hacer que las cadenas se separen entre sí, reduciendo la T g . Si un plástico con algunas propiedades deseables tiene una T g demasiado alta, a veces se puede combinar con otro en un copolímero o material compuesto con una T g por debajo de la temperatura de uso previsto. Tenga en cuenta que algunos plásticos se utilizan a altas temperaturas, por ejemplo, en motores de automóviles, y otros a bajas temperaturas. [32]
En los materiales viscoelásticos , la presencia de un comportamiento similar al de un líquido depende de las propiedades de estos y, por lo tanto, varía con la velocidad de aplicación de la carga, es decir, con la rapidez con la que se aplica una fuerza. El juguete de silicona Silly Putty se comporta de manera bastante diferente según la velocidad de aplicación de la fuerza: si se tira lentamente, fluye y actúa como un líquido muy viscoso; si se golpea con un martillo, se rompe y actúa como un vaso de vidrio.
Al enfriarse, el caucho experimenta una transición de líquido a vidrio , también llamada transición caucho-vidrio .
Mecánica de la vitrificación
El movimiento molecular en materia condensada puede representarse mediante una serie de Fourier cuya interpretación física consiste en una superposición de ondas longitudinales y transversales de desplazamiento atómico con direcciones y longitudes de onda variables. En los sistemas monoatómicos, estas ondas se denominan fluctuaciones de densidad . (En los sistemas poliatómicos, también pueden incluir fluctuaciones de composición.) [55]
Por lo tanto, el movimiento térmico en líquidos puede descomponerse en vibraciones longitudinales elementales (o fonones acústicos ), mientras que las vibraciones transversales (u ondas de corte) se describieron originalmente solo en sólidos elásticos que exhiben el estado cristalino altamente ordenado de la materia. En otras palabras, los líquidos simples no pueden soportar una fuerza aplicada en forma de tensión de corte y cederán mecánicamente a través de una deformación plástica macroscópica (o flujo viscoso). Además, el hecho de que un sólido se deforme localmente mientras retiene su rigidez , mientras que un líquido cede a un flujo viscoso macroscópico en respuesta a la aplicación de una fuerza de corte aplicada , es aceptado por muchos como la distinción mecánica entre los dos. [56] [57]
Sin embargo, Frenkel señaló las deficiencias de esta conclusión en su revisión de la teoría cinética de los sólidos y la teoría de la elasticidad en líquidos . Esta revisión se desprende directamente de la característica continua del paso viscoelástico del estado líquido al sólido cuando la transición no está acompañada de cristalización, es decir, el líquido viscoso superenfriado . De este modo, vemos la íntima correlación entre los fonones acústicos transversales (u ondas de corte) y el inicio de la rigidez tras la vitrificación , como describe Bartenev en su descripción mecánica del proceso de vitrificación. [58] [59]
Las velocidades de los fonones acústicos longitudinales en materia condensada son directamente responsables de la conductividad térmica que nivela los diferenciales de temperatura entre elementos de volumen comprimidos y expandidos . Kittel propuso que el comportamiento de los vidrios se interpreta en términos de un " recorrido libre medio " aproximadamente constante para los fonones reticulares, y que el valor del recorrido libre medio es del orden de magnitud de la escala de desorden en la estructura molecular de un líquido o sólido. Se han graficado los recorridos libres medios de los fonones térmicos o las longitudes de relajación de varios formadores de vidrio en función de la temperatura de transición vítrea, lo que indica una relación lineal entre ambos. Esto ha sugerido un nuevo criterio para la formación de vidrio basado en el valor del recorrido libre medio de los fonones. [60]
Se ha sugerido a menudo que el transporte de calor en sólidos dieléctricos se produce a través de vibraciones elásticas de la red, y que este transporte está limitado por la dispersión elástica de fonones acústicos por defectos de la red (por ejemplo, vacantes espaciadas aleatoriamente). [61] Estas predicciones fueron confirmadas por experimentos en vidrios comerciales y vitrocerámicas , donde los caminos libres medios estaban aparentemente limitados por la "dispersión de límites internos" a escalas de longitud de 10-100 micrómetros (0,00039-0,00394 pulgadas). [62] [63] La relación entre estas ondas transversales y el mecanismo de vitrificación ha sido descrita por varios autores que propusieron que el inicio de correlaciones entre tales fonones da como resultado un ordenamiento orientacional o "congelación" de las tensiones de corte locales en los líquidos formadores de vidrio, produciendo así la transición vítrea. [64]
Estructura electrónica
La influencia de los fonones térmicos y su interacción con la estructura electrónica es un tema que se introdujo apropiadamente en una discusión sobre la resistencia de los metales líquidos. Se hace referencia a la teoría de la fusión de Lindemann [65] y se sugiere que la caída de la conductividad al pasar del estado cristalino al líquido se debe a la mayor dispersión de los electrones de conducción como resultado de la mayor amplitud de la vibración atómica . Tales teorías de localización se han aplicado al transporte en vidrios metálicos , donde el camino libre medio de los electrones es muy pequeño (del orden del espaciamiento interatómico). [66] [67]
La formación de una forma no cristalina de una aleación de oro y silicio mediante el método de enfriamiento por salpicadura a partir de la masa fundida condujo a consideraciones adicionales sobre la influencia de la estructura electrónica en la capacidad de formación de vidrio, en función de las propiedades del enlace metálico . [68] [69] [70] [71] [72]
Otros trabajos indican que la movilidad de los electrones localizados se ve mejorada por la presencia de modos fonónicos dinámicos. Una afirmación en contra de este modelo es que si los enlaces químicos son importantes, los modelos de electrones casi libres no deberían ser aplicables. Sin embargo, si el modelo incluye la acumulación de una distribución de carga entre todos los pares de átomos al igual que un enlace químico (por ejemplo, silicio, cuando una banda está simplemente llena de electrones), entonces debería aplicarse a los sólidos . [73]
Por lo tanto, si la conductividad eléctrica es baja, el camino libre medio de los electrones es muy corto. Los electrones solo serán sensibles al orden de corto alcance en el vidrio, ya que no tienen la oportunidad de dispersarse de los átomos espaciados a grandes distancias. Dado que el orden de corto alcance es similar en vidrios y cristales, las energías electrónicas deberían ser similares en estos dos estados. Para aleaciones con menor resistividad y caminos libres medios electrónicos más largos, los electrones podrían comenzar a sentir [ dudoso – discutir ] que hay desorden en el vidrio, y esto aumentaría sus energías y desestabilizaría el vidrio con respecto a la cristalización. Por lo tanto, las tendencias de formación de vidrio de ciertas aleaciones pueden deberse en parte al hecho de que los caminos libres medios de los electrones son muy cortos, de modo que solo el orden de corto alcance es importante para la energía de los electrones.
También se ha argumentado que la formación de vidrio en sistemas metálicos está relacionada con la "suavidad" del potencial de interacción entre átomos diferentes. Algunos autores, haciendo hincapié en las fuertes similitudes entre la estructura local del vidrio y el cristal correspondiente, sugieren que el enlace químico ayuda a estabilizar la estructura amorfa. [74] [75]
Otros autores han sugerido que la estructura electrónica influye en la formación de vidrio a través de las propiedades direccionales de los enlaces. Por lo tanto, la no cristalinidad se ve favorecida en elementos con un gran número de formas polimórficas y un alto grado de anisotropía de enlace . La cristalización se vuelve más improbable a medida que aumenta la anisotropía de enlace de metálico isótropo a metálico anisotrópico a enlace covalente , lo que sugiere una relación entre el número de grupo en la tabla periódica y la capacidad de formación de vidrio en sólidos elementales . [76]
Véase también
Referencias
- ^ Warren, BE (agosto de 1941). "RESUMEN DEL TRABAJO SOBRE LA DISPOSICIÓN ATÓMICA EN EL VIDRIO*". Journal of the American Ceramic Society . 24 (8): 256–261. doi :10.1111/j.1151-2916.1941.tb14858.x. ISSN 0002-7820.
- ^ ab ISO 11357-2: Plásticos – Calorimetría diferencial de barrido – Parte 2: Determinación de la temperatura de transición vítrea (1999).
- ^ "La transición vítrea". Centro de aprendizaje de la ciencia de los polímeros. Archivado desde el original el 15 de enero de 2019. Consultado el 15 de octubre de 2009 .
- ^ ab Debenedetti, PG; Stillinger (2001). "Líquidos superenfriados y la transición vítrea". Nature . 410 (6825): 259–267. Bibcode :2001Natur.410..259D. doi :10.1038/35065704. PMID 11258381. S2CID 4404576.
- ^ ab Angell, CA; Ngai, KL; McKenna, GB; McMillan, PF; Martin, SW (2000). "Relajación en líquidos formadores de vidrio y sólidos amorfos". Appl. Phys. Rev. 88 ( 6): 3113–3157. Bibcode :2000JAP....88.3113A. doi :10.1063/1.1286035. Archivado desde el original el 2020-03-07 . Consultado el 2018-09-06 .
- ^ ab Zarzycki, J. (1991). Vidrios y estado vítreo. Cambridge University Press. ISBN 978-0521355827Archivado desde el original el 2020-08-02 . Consultado el 2016-09-23 .
- ^ Ojovan, MI (2004). "Formación de vidrio en SiO 2 amorfo como una transición de fase de percolación en un sistema de defectos de red". Journal of Experimental and Theoretical Physics Letters . 79 (12): 632–634. Bibcode :2004JETPL..79..632O. doi :10.1134/1.1790021. S2CID 124299526.
- ^ ab Meille Stefano, V.; Allegra, G.; Geil Phillip, H.; He, J.; Hess, M.; Jin, J.-I.; Kratochvíl, P.; Mormann, W.; Stepto, R. (2011). "Definiciones de términos relacionados con polímeros cristalinos (Recomendaciones IUPAC 2011)" (PDF) . Química Pura y Aplicada . 83 (10): 1831. doi :10.1351/PAC-REC-10-11-13. S2CID 98823962. Archivado (PDF) desde el original el 25 de junio de 2018 . Consultado el 25 de junio de 2018 .
- ^ IUPAC , Compendio de terminología química , 2.ª ed. (el "Libro de oro") (1997). Versión corregida en línea: (2006–) "transición vítrea". doi :10.1351/goldbook.G02640
- ^ Hansen, J.-P.; McDonald, IR (2007). Teoría de líquidos simples. Elsevier. pp. 250–254. ISBN 978-0123705358Archivado desde el original el 21 de septiembre de 2013. Consultado el 23 de septiembre de 2016 .
- ^ Adam, JL; Zhang, X. (14 de febrero de 2014). Vidrios de calcogenuro: preparación, propiedades y aplicaciones. Elsevier Science. pág. 94. ISBN 978-0-85709-356-1Archivado desde el original el 17 de julio de 2017 . Consultado el 2 de mayo de 2017 .
- ^ Phillips, JC (1979). "Topología de sólidos no cristalinos covalentes I: orden de corto alcance en aleaciones de calcogenuro". Journal of Non-Crystalline Solids . 34 (2): 153. Bibcode :1979JNCS...34..153P. doi :10.1016/0022-3093(79)90033-4.
- ^ Moynihan, C. et al. (1976) en La transición vítrea y la naturaleza del estado vítreo , M. Goldstein y R. Simha (Eds.), Ann. NY Acad. Sci., Vol. 279. ISBN 0890720533 .
- ^ Angell, CA (1988). "Perspectiva sobre la transición vítrea". Revista de Física y Química de Sólidos . 49 (8): 863–871. Bibcode :1988JPCS...49..863A. doi :10.1016/0022-3697(88)90002-9.
- ^ Ediger, MD; Angell, CA; Nagel, Sidney R. (1996). "Líquidos y vidrios superenfriados". The Journal of Physical Chemistry . 100 (31): 13200. doi :10.1021/jp953538d.
- ^ Angell, CA (1995). "Formación de vidrios a partir de líquidos y biopolímeros". Science . 267 (5206): 1924–35. Bibcode :1995Sci...267.1924A. doi :10.1126/science.267.5206.1924. PMID 17770101. S2CID 927260.
- ^ Stillinger, FH (1995). "Una vista topográfica de los líquidos superenfriados y la formación de vidrio". Science . 267 (5206): 1935–9. Bibcode :1995Sci...267.1935S. doi :10.1126/science.267.5206.1935. PMID 17770102. S2CID 30407650.
- ^ Nemilov SV (1994). Aspectos termodinámicos y cinéticos del estado vítreo . CRC Press. ISBN 978-0849337826.
- ^ Gibbs, JH (1960). MacKenzie, JD (ed.). Aspectos modernos del estado vítreo . Butterworth. OCLC 1690554.
- ^ Ojovan, Michael I; Lee, William (Bill) E (2010). "Conectividad y transición vítrea en sistemas de óxido desordenados". Journal of Non-Crystalline Solids . 356 (44–49): 2534. Bibcode :2010JNCS..356.2534O. doi :10.1016/j.jnoncrysol.2010.05.012.
- ^ Sturm, Karl Günter (2017). "Modelo microscópico-fenomenológico de la transición vítrea I. Fundamentos del modelo (versión revisada y mejorada) (título anterior: Modelo microscópico de la transformación vítrea y las traducciones moleculares en líquidos I. Fundamentos del modelo-octubre de 2015)". Cerámica . doi :10.13140/RG.2.2.19831.73121.
- ^ "¿Qué son las pruebas mecánicas dinámicas (DMA)?". 2018. Archivado desde el original el 2020-11-17 . Consultado el 2020-12-09 .
- ^ ab Zanotto, Edgar D.; Mauro, John C. (septiembre de 2017). "El estado vítreo de la materia: su definición y destino final". Journal of Non-Crystalline Solids . 471 : 490–495. Código Bibliográfico :2017JNCS..471..490Z. doi :10.1016/j.jnoncrysol.2017.05.019.
- ^ Simón, Franz (1 de abril de 1927). "Zum Prinzip von der Unerreichbarkeit des absolutan Nullpunktes". Zeitschrift für Physik (en alemán). 41 (4): 806–809. Código Bib : 1927ZPhy...41..806S. doi :10.1007/BF01395487. ISSN 0044-3328.
- ^ Zachariasen, WH (octubre de 1932). "La disposición atómica en vidrio". Revista de la Sociedad Química Estadounidense . 54 (10): 3841–3851. doi :10.1021/ja01349a006. ISSN 0002-7863.
- ^ Gupta, Prabhat K. (febrero de 1996). "Sólidos no cristalinos: vidrios y sólidos amorfos". Journal of Non-Crystalline Solids . 195 (1–2): 158–164. Bibcode :1996JNCS..195..158G. doi :10.1016/0022-3093(95)00502-1.
- ^ Gutzow, Ivan S.; Schmelzer, Jürn WP (2013). El estado vítreo: termodinámica, estructura, reología y cristalización. Berlín, Heidelberg: Springer Berlin Heidelberg. p. 124. doi :10.1007/978-3-642-34633-0. ISBN 978-3-642-34632-3.
- ^ Medición de Tg ab de vidrios Archivado el 17 de abril de 2009 en Wayback Machine . Glassproperties.com. Recuperado el 29 de junio de 2012.
- ^ IUPAC , Compendio de terminología química , 2.ª ed. (el "Libro de oro") (1997). Versión corregida en línea: (2006–) "temperatura de transición vítrea". doi :10.1351/goldbook.G02641
- ^ EU WO03053721, "NEUMÁTICO QUE COMPRENDE UN POLÍMERO DE CICLOOLEFINA, UNA BANDA DE RODAMIENTO Y UNA COMPOSICIÓN ELASTOMÉRICA UTILIZADA EN EL MISMO", expedida el 7 de marzo de 2003
- ^ abc Ibeh, Christopher C. (2011). MATERIALES TERMOPLÁSTICOS Propiedades, métodos de fabricación y aplicaciones . CRC Press. págs. 491–497. ISBN 978-1-4200-9383-4.
- ^ abcdefghijkl Wilkes, CE (2005). Manual de PVC. Hanser Verlag. ISBN 978-1-56990-379-7Archivado desde el original el 3 de abril de 2022. Consultado el 23 de septiembre de 2016 .
- ^ ABS.nrri.umn.edu
- ^ Nicholson, John W. (2011). La química de los polímeros (4.ª edición revisada). Royal Society of Chemistry. pág. 50. ISBN 9781849733915Archivado desde el original el 10 de abril de 2022 . Consultado el 10 de septiembre de 2013 .
- ^ Información y propiedades del nailon-6 Archivado el 10 de enero de 2012 en Wayback Machine . Polymerprocessing.com (15 de abril de 2001). Consultado el 29 de junio de 2012.
- ^ Jones, A (2014). "Materiales complementarios para músculos artificiales a partir de hilo de pescar e hilo de coser". Science . 343 (6173): 868–72. Bibcode :2014Sci...343..868H. doi :10.1126/science.1246906. PMID 24558156. S2CID 16577662.
- ^ Medición de los efectos de la humedad en las propiedades mecánicas del nailon 66. Resumen de la aplicación de análisis térmico TA-133 de TA Instruments
- ^ PCL | Aplicaciones y usos finales | Polietileno Archivado el 5 de junio de 2013 en Wayback Machine . Polyesterconverters.com. Consultado el 29 de junio de 2012.
- ^ EPCOS 2007: Transición vítrea y cristalización en materiales de cambio de fase Archivado el 26 de julio de 2011 en Wayback Machine . Consultado el 29 de junio de 2012.
- ^ Bucaro, JA (1974). "Dispersión de Brillouin a alta temperatura en cuarzo fundido". Journal of Applied Physics . 45 (12): 5324–5329. Bibcode :1974JAP....45.5324B. doi :10.1063/1.1663238.
- ^ ab Pohl, RO; Love, WF; Stephens, RB (1973-08-01). Vibraciones reticulares en sólidos no cristalinos (informe). Universidad de Cornell, Ithaca, NY (EE. UU.). Laboratorio de Física Atómica y del Estado Sólido. OSTI 4410557.
- ^ Zeller, RC; Pohl, RO (15 de septiembre de 1971). "Conductividad térmica y calor específico de sólidos no cristalinos". Physical Review B . 4 (6): 2029–2041. Código Bibliográfico :1971PhRvB...4.2029Z. doi :10.1103/PhysRevB.4.2029.
- ^ Anderson, P. w.; Halperin, BI; Varma, c. M. (enero de 1972). "Propiedades térmicas anómalas de baja temperatura de vidrios y vidrios de espín". Revista filosófica . 25 (1): 1–9. Bibcode :1972PMag...25....1A. doi :10.1080/14786437208229210. ISSN 0031-8086.
- ^ Kauzmann, Walter (1948). "La naturaleza del estado vítreo y el comportamiento de los líquidos a bajas temperaturas". Chemical Reviews . 43 (2): 219–256. doi :10.1021/cr60135a002.
- ^ ab Wolchover, Natalie (11 de marzo de 2020). «El vidrio ideal explicaría por qué existe el vidrio». Quanta Magazine . Archivado desde el original el 7 de abril de 2020. Consultado el 3 de abril de 2020 .
- ^ Gibbs, Julian H.; DiMarzio, Edmund A. (1958-03-01). "Naturaleza de la transición vítrea y del estado vítreo". The Journal of Chemical Physics . 28 (3): 373–383. Bibcode :1958JChPh..28..373G. doi :10.1063/1.1744141. ISSN 0021-9606.
- ^ Swallen, Stephen F.; Kearns, Kenneth L.; Mapes, Marie K.; Kim, Yong Seol; McMahon, Robert J.; Ediger, MD; Wu, Tian; Yu, Lian; Satija, Sushil (19 de enero de 2007). "Vidrios orgánicos con estabilidad termodinámica y cinética excepcional". Science . 315 (5810): 353–356. Bibcode :2007Sci...315..353S. doi :10.1126/science.1135795. ISSN 0036-8075. PMID 17158289.
- ^ Ojovan MI (2008). "Configuraciones: parámetros termodinámicos y cambios de simetría en la transición vítrea" (PDF) . Entropy . 10 (3): 334–364. Bibcode :2008Entrp..10..334O. doi : 10.3390/e10030334 . Archivado (PDF) desde el original el 2009-07-11 . Consultado el 2009-09-25 .
- ^ Ojovan, MI (2008). "Configuraciones: parámetros termodinámicos y cambios de simetría en la transición vítrea" (PDF) . Entropy . 10 (3): 334–364. Bibcode :2008Entrp..10..334O. doi : 10.3390/e10030334 . Archivado (PDF) desde el original el 2009-07-11 . Consultado el 2009-09-25 .
- ^ Ojovan, Michael I; Travis, Karl P; Hand, Russell J (2007). "Parámetros termodinámicos de enlaces en materiales vítreos a partir de relaciones viscosidad-temperatura" (PDF) . Journal of Physics: Condensed Matter . 19 (41): 415107. Bibcode :2007JPCM...19O5107O. doi :10.1088/0953-8984/19/41/415107. PMID 28192319. S2CID 24724512. Archivado (PDF) desde el original el 25 de julio de 2018 . Consultado el 6 de julio de 2019 .
- ^ Nguyen, Huy; Lia, Can; Wallum, Alison; Lyding, Joseph; Gruebele, Martin (2019). "Dinámica multiescala en la superficie de sílice vítrea". J. Chem. Phys . 151 (1): 62–68. doi :10.1038/nphys1432. PMC 2844102. PMID 20336168 .
- ^ Wolynes, PG; Stevenson, JD (2009). "Un origen universal para las relajaciones secundarias en líquidos superenfriados y vidrios estructurales". Nature Physics . 6 (1): 62–68. doi : 10.1063/1.5123228 . PMC 2844102 . PMID 20336168.
- ^ Cowie, JMG y Arrighi, V., Polímeros: química y física de materiales modernos, 3.ª edición (CRC Press, 2007) ISBN 0748740732
- ^ Capponi, S.; Alvarez, F.; Racko, D. (2020), "Volumen libre en una solución de polímero PVME-agua", Macromolecules , 53 (12): 4770–4782, Bibcode :2020MaMol..53.4770C, doi :10.1021/acs.macromol.0c00472, hdl : 10261/218380 , S2CID 219911779
- ^ Slater, JC, Introducción a la física química (3.ª edición, Martindell Press, 2007) ISBN 1178626598
- ^ Born, Max (2008). "Sobre la estabilidad de las redes cristalinas. I". Actas matemáticas de la Cambridge Philosophical Society . 36 (2): 160–172. Bibcode :1940PCPS...36..160B. doi :10.1017/S0305004100017138. S2CID 104272002.
- ^ Born, Max (1939). "Termodinámica de cristales y fusión". The Journal of Chemical Physics . 7 (8): 591–603. Código Bibliográfico :1939JChPh...7..591B. doi :10.1063/1.1750497.
- ^ Frenkel, J. (1946). Teoría cinética de líquidos. Clarendon Press, Oxford.
- ^ Bartenev, GM, Estructura y propiedades mecánicas de vidrios inorgánicos (Wolters – Noordhoof, 1970) ISBN 9001054501
- ^ Reynolds, CL Jr. (1979). "Correlación entre el camino libre medio de fonones de baja temperatura y la temperatura de transición vítrea en sólidos amorfos". J. Non-Cryst. Solids . 30 (3): 371. Bibcode :1979JNCS...30..371R. doi :10.1016/0022-3093(79)90174-1.
- ^ Rosenburg, HM (1963) Física del estado sólido a baja temperatura . Clarendon Press, Oxford.
- ^ Kittel, C. (1946). "Propagación ultrasónica en líquidos". J. Chem. Phys . 14 (10): 614. Bibcode :1946JChPh..14..614K. doi :10.1063/1.1724073. hdl : 1721.1/5041 .
- ^ Kittel, C. (1949). "Interpretación de la conductividad térmica de los vidrios". Phys. Rev . 75 (6): 972. Bibcode :1949PhRv...75..972K. doi :10.1103/PhysRev.75.972.
- ^ Chen, Shao-Ping; Egami, T.; Vitek, V. (1985). "Ordenamiento orientacional de tensiones cortantes locales en líquidos: ¿una transición de fase?". Journal of Non-Crystalline Solids . 75 (1–3): 449. Bibcode :1985JNCS...75..449C. doi :10.1016/0022-3093(85)90256-X.
- ^ Sorkin, Viacheslav (2005). "Criterio de Lindemann" (PDF) . Defectos puntuales, estructura reticular y fusión (MSc). Instituto Tecnológico de Israel. págs. 5–8. Archivado (PDF) desde el original el 19 de agosto de 2019. Consultado el 6 de enero de 2022 .
- ^ Mott, NF (1934). "La resistencia de los metales líquidos". Actas de la Royal Society A . 146 (857): 465. Bibcode :1934RSPSA.146..465M. doi : 10.1098/rspa.1934.0166 .
- ^ Lindemann, C. (1911). "Sobre el cálculo de frecuencias naturales moleculares". Phys. Z. 11 : 609.
- ^ Klement, W.; Willens, RH; Duwez, POL (1960). "Estructura no cristalina en aleaciones solidificadas de oro y silicio". Nature . 187 (4740): 869. Bibcode :1960Natur.187..869K. doi :10.1038/187869b0. S2CID 4203025.
- ^ Duwez, Pol; Willens, RH; Klement, W. (1960). "Serie continua de soluciones sólidas metaestables en aleaciones de plata y cobre" (PDF) . Journal of Applied Physics . 31 (6): 1136. Bibcode :1960JAP....31.1136D. doi :10.1063/1.1735777. Archivado (PDF) desde el original el 2017-12-02 . Consultado el 2018-05-16 .
- ^ Duwez, Pol; Willens, RH; Klement, W. (1960). "Compuesto electrónico metaestable en aleaciones de plata y titanio" (PDF) . Journal of Applied Physics . 31 (6): 1137. Bibcode :1960JAP....31.1137D. doi :10.1063/1.1735778. Archivado (PDF) desde el original el 2020-04-18 . Consultado el 2019-07-06 .
- ^ Chaudhari, P; Turnbull, D (1978). "Estructura y propiedades de vidrios metálicos". Science . 199 (4324): 11–21. Bibcode :1978Sci...199...11C. doi :10.1126/science.199.4324.11. PMID 17841932. S2CID 7786426.
- ^ Chen, JS (1980). "Metales vítreos". Informes sobre el progreso en física . 43 (4): 353. Bibcode :1980RPPh...43..353C. doi :10.1088/0034-4885/43/4/001. S2CID 250804009.
- ^ Jonson, M.; Girvin, SM (1979). "Dinámica electrón-fonón y anomalías de transporte en aleaciones metálicas aleatorias". Phys. Rev. Lett . 43 (19): 1447. Bibcode :1979PhRvL..43.1447J. doi :10.1103/PhysRevLett.43.1447.
- ^ Turnbull, D. (1974). "Formación de sólidos amorfos y comportamiento de la solución intersticial en sistemas de aleación metálica". J. Phys. C . 35 (C4): C4–1. CiteSeerX 10.1.1.596.7462 . doi :10.1051/jphyscol:1974401. S2CID 52102270.
- ^ Chen, HS; Park, BK (1973). "El papel del enlace químico en los vidrios metálicos". Acta Metall . 21 (4): 395. doi :10.1016/0001-6160(73)90196-X.
- ^ Wang, R.; Merz, D. (1977). "Enlace polimórfico y estabilidad térmica de sólidos elementales no cristalinos". Physica Status Solidi A . 39 (2): 697. Bibcode :1977PSSAR..39..697W. doi :10.1002/pssa.2210390240.
Enlaces externos
- Fragilidad Archivado el 28 de junio de 2007 en Wayback Machine.
- Ecuación VFT.
- Polímeros I
- Polímeros II Archivado el 11 de enero de 2010 en Wayback Machine.
- Angell: Medios acuosos
- Paquete de enseñanza y aprendizaje DoITPoMS: “La transición vítrea en polímeros”
- Breve descripción de la temperatura de transición vítrea















