Tangrama

El tangram ( chino :七巧板; pinyin : qīqiǎobǎn ; lit. 'siete tableros de habilidad') es un rompecabezas de disección que consiste en siete polígonos planos, llamados tans , que se juntan para formar formas. El objetivo es replicar un patrón (dado solo un contorno) que generalmente se encuentra en un libro de rompecabezas usando las siete piezas sin superposición. Alternativamente, los tangram se pueden usar para crear diseños minimalistas originales que son apreciados por sus méritos estéticos inherentes o como base para desafiar a otros a replicar su contorno. Se dice que fue inventado en China en algún momento alrededor de fines del siglo XVIII y luego trasladado a América y Europa por barcos mercantes poco después. ^[1] Se volvió muy popular en Europa por un tiempo, y luego nuevamente durante la Primera Guerra Mundial . Es uno de los rompecabezas de disección más reconocidos en el mundo y se ha utilizado para varios propósitos, incluidos la diversión, el arte y la educación. ^{[2] [3] [4]}

El origen de la palabra inglesa «tangram» no está claro. Una conjetura sostiene que es un compuesto del elemento griego «-gram», derivado de γράμμα («carácter escrito, letra, aquello que se dibuja»), y que el elemento «tan-» puede ser el chino t'an , «extender», o el cantonés t'ang , «chino». ^[5] Otra posibilidad es que la palabra derive del arcaico inglés «tangram», que significa «algo extraño, intrincadamente elaborado». ^[6]

En cualquier caso, se cree que el primer uso conocido de la palabra se encuentra en el libro de 1848 Geometrical Puzzle for the Young del matemático y futuro presidente de la Universidad de Harvard, Thomas Hill . ^[7] Hill probablemente acuñó el término en el mismo trabajo y promovió vigorosamente la palabra en numerosos artículos que abogaban por el uso del rompecabezas en la educación, y en 1864 la palabra recibió reconocimiento oficial en el idioma inglés cuando se incluyó en el Diccionario americano de Noah Webster . ^[8]

A pesar de su aparición relativamente reciente en Occidente, existe una tradición mucho más antigua de juegos de disección en China que probablemente haya desempeñado un papel en su inspiración. En particular, las mesas modulares de banquete de la dinastía Song guardan un parecido asombroso con las piezas del tangram y había libros dedicados a organizarlas para formar patrones agradables. ^[9]

Varias fuentes chinas informan ampliamente sobre un conocido erudito de la dinastía Song, Huang Bosi 黄伯思, que desarrolló una forma de entretenimiento para sus invitados a la cena basada en arreglos creativos de seis mesas pequeñas llamadas 宴几 o 燕几 ( mesas de banquete o mesas de golondrinas , respectivamente). Un diagrama las muestra como rectángulos oblongos, y otros informes sugieren que una séptima mesa fue añadida más tarde, tal vez por un inventor posterior.

Según fuentes occidentales, sin embargo, se desconoce el inventor chino histórico del tangram, salvo a través del seudónimo Yang-cho-chu-shih (recluso tonto (?), recluso = 处士). Se cree que el rompecabezas se introdujo originalmente en un libro titulado Ch'i chi'iao t'u , que ya había sido reportado como perdido en 1815 por Shan-chiao en su libro Nuevas figuras del tangram . Sin embargo, se cree generalmente que el rompecabezas fue inventado unos 20 años antes. ^[10]

El destacado matemático del siglo III Liu Hui utilizó pruebas de construcción en sus obras y algunas guardan un parecido sorprendente con las mesas de banquete desarrolladas posteriormente, que a su vez parecen anticipar el tangram. Si bien no hay motivos para sospechar que se usaron tangrams en la prueba del teorema de Pitágoras , como a veces se informa, es probable que este estilo de razonamiento geométrico ejerciera una influencia en la vida cultural china que condujo directamente al rompecabezas. ^[11]

Los primeros años de intentos de datar el Tangram se vieron confusos por la historia popular pero fraudulenta escrita por el famoso fabricante de rompecabezas Samuel Loyd en su obra de 1908 El octavo libro de Tan . Esta obra contiene muchas características extravagantes que despertaron tanto interés como sospecha entre los académicos contemporáneos que intentaron verificar el relato. En 1910 estaba claro que era un engaño. Una carta fechada en este año del editor del Oxford Dictionary Sir James Murray en nombre de varios académicos chinos al destacado acertijo Henry Dudeney dice: "El resultado ha sido demostrar que el hombre Tan, el dios Tan y el Libro de Tan son completamente desconocidos para la literatura, la historia o la tradición chinas". ^[6] Junto con sus muchos detalles extraños, la fecha de creación del Octavo Libro de Tan para el rompecabezas de 4000 años de antigüedad tuvo que considerarse completamente infundada y falsa.

El tangram más antiguo que se conserva fue entregado al magnate naviero y congresista de Filadelfia Francis Waln en 1802, pero no fue hasta más de una década después que el público occidental, en general, se familiarizaría con el rompecabezas. ^[1] En 1815, el capitán estadounidense M. Donnaldson recibió un par de libros del autor Sang-Hsia-koi sobre el tema (un libro de problemas y otro de soluciones) cuando su barco, el Trader, atracó allí. Luego fueron llevados con el barco a Filadelfia, en febrero de 1816. El primer libro de tangram que se publicó en Estados Unidos se basó en el par que trajo Donnaldson. ^[12]

El rompecabezas llegó finalmente a Inglaterra, donde se puso muy de moda. La locura se extendió rápidamente a otros países europeos. Esto se debió principalmente a un par de libros de tangram británicos, The Fashionable Chinese Puzzle , y el libro de soluciones que lo acompañaba, Key . ^[13] Pronto, los juegos de tangram se exportaron en gran cantidad desde China, hechos de varios materiales, desde vidrio hasta madera y caparazón de tortuga. ^[14]

Muchos de estos inusuales y exquisitos juegos de tangram llegaron a Dinamarca . El interés danés por los tangrams se disparó alrededor de 1818, cuando se publicaron dos libros sobre el rompecabezas, lo que generó mucho entusiasmo. ^[15] El primero de ellos fue Mandarinen (Sobre el juego chino). Fue escrito por un estudiante de la Universidad de Copenhague y era una obra de no ficción sobre la historia y la popularidad de los tangrams. El segundo, Det nye chinesiske Gaadespil (El nuevo juego de rompecabezas chino), constaba de 339 rompecabezas copiados del Octavo Libro de Tan , así como un original. ^[15]

Un factor que contribuyó a la popularidad del juego en Europa fue que, aunque la Iglesia Católica prohibía muchas formas de recreación en el día de reposo, no ponía objeciones a los juegos de rompecabezas como el tangram. ^[16]

Los tangrams fueron presentados por primera vez al público alemán por el industrial Friedrich Adolf Richter alrededor de 1891. ^[17] Los juegos estaban hechos de piedra o barro falso , ^[18] y se comercializaban bajo el nombre de "El rompecabezas del ancla". ^[17]

En el plano internacional, la Primera Guerra Mundial fue testigo de un gran resurgimiento del interés por los tangrams, tanto en el frente interno como en las trincheras de ambos bandos. Durante esta época, se lo conocía ocasionalmente con el nombre de "La Esfinge ", un título alternativo para los juegos de "rompecabezas de anclas". ^{[19] [20]}

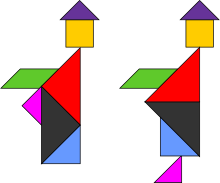
Una paradoja del tangram es una falacia de disección: dos figuras compuestas con el mismo conjunto de piezas, una de las cuales parece ser un subconjunto propio de la otra. ^[21] Una paradoja famosa es la de los dos monjes , atribuida a Henry Dudeney , que consiste en dos formas similares, una con pie y la otra sin él. ^[22] En realidad, el área del pie está compensada en la segunda figura por un cuerpo sutilmente más grande.

La paradoja de los dos monjes: dos formas similares pero a una le falta un pie:

La paradoja del tangram del cubilete mágico, del libro de Sam Loyd The 8th Book of Tan (1903). ^[23] Cada uno de estos cubiletes se compuso utilizando las mismas siete formas geométricas. Pero el primero está completo y los demás contienen huecos de distintos tamaños. (Observe que el de la izquierda es ligeramente más corto que los otros dos. El del medio es ligeramente más ancho que el de la derecha y el de la izquierda es aún más angosto.) ^[24]

Paradoja del tangram de cuadrados recortados – del libro de Loyd El octavo libro de Tan (1903): ^[23]

Las figuras séptima y octava representan el cuadrado misterioso, construido con siete piezas: luego con una esquina cortada, y todavía las mismas siete piezas empleadas. ^[25]

Se han creado más de 6500 problemas de tangram diferentes a partir de textos del siglo XIX únicamente, y el número actual está en constante crecimiento. ^[26] Fu Traing Wang y Chuan-Chih Hsiung demostraron en 1942 que solo hay trece configuraciones de tangram convexas (los segmentos dibujados entre dos puntos cualesquiera en la configuración siempre están completamente contenidos dentro de la configuración, es decir, configuraciones sin huecos en el contorno). ^{[27] [28]}

Eligiendo una unidad de medida de modo que las siete piezas se puedan ensamblar para formar un cuadrado de lado una unidad y que tenga área una unidad cuadrada, las siete piezas son: ^[29]

• 2 triángulos rectángulos grandes (hipotenusa 1, lados ⁠√ 2/2⁠ , área ⁠1/4⁠ )
• 1 triángulo rectángulo mediano (hipotenusa ⁠√ 2/2⁠ , lados ⁠1/2⁠ , área ⁠1/8⁠ )
• 2 triángulos rectángulos pequeños (hipotenusa ⁠1/2⁠ , lados ⁠√ 2/4⁠ , área ⁠1/16⁠ )
• 1 cuadrado (lados ⁠√ 2/4⁠ , área ⁠1/8⁠ )
• 1 paralelogramo (lados de ⁠1/2⁠ y ⁠√ 2/4⁠ , altura de ⁠1/4⁠ , área ⁠1/8⁠ )

De estas siete piezas, el paralelogramo es único en el sentido de que no tiene simetría de reflexión , sino solo simetría rotacional , por lo que su imagen especular solo se puede obtener al darle la vuelta. Por lo tanto, es la única pieza que puede ser necesario dar vuelta para formar ciertas formas.

• Tangram (videojuego)
• Huevo de Colón (rompecabezas de tangram)
• Rompecabezas matemático
• Ostomachion
• Rompecabezas de mosaicos
• Pickagram (rompecabezas magnético en 3D de tangram)
• Bloques de atributos

Fuentes

• Slocum, Jerry (2001). El Tao del Tangram . Barnes & Noble. ISBN 978-1-4351-0156-2.
• Slocum, Jerry (2003). El libro del tangram . Sterling. ISBN 978-1-4027-0413-0.

• Anno, Mitsumasa. Juegos de matemáticas de Anno (tres volúmenes). Nueva York: Philomel Books, 1987. ISBN 0-399-21151-9 (v. 1), ISBN 0-698-11672-0 (v. 2), ISBN 0-399-22274-X (v. 3).   
• Botermans, Jack, et al. El mundo de los juegos: sus orígenes e historia, cómo jugarlos y cómo crearlos (traducción de Wereld vol spelletjes ). Nueva York: Facts on File, 1989. ISBN 0-8160-2184-8 . 
• Dudeney, HE Diversiones en matemáticas . Nueva York: Dover Publications, 1958.
• Gardner, Martin . "Juegos matemáticos: sobre la fantástica historia y los desafíos creativos del juego de rompecabezas de los tangramas", Scientific American, agosto de 1974, págs. 98-103.
• Gardner, Martin. "Más sobre los tangramas", Scientific American, septiembre de 1974, págs. 187-191.
• Gardner, Martin. El segundo libro de Scientific American sobre acertijos y diversiones matemáticas . Nueva York: Simon & Schuster, 1961. ISBN 0-671-24559-7 . 
• Loyd, Sam. Sam Loyd's Book of Tangram Puzzles (El octavo libro de Tan, parte I) . Mineola, Nueva York: Dover Publications, 1968.
• Slocum, Jerry, et al. Puzzles of Old and New: How to Make and Solve Them . De Meern, Países Bajos: Plenary Publications International (Europa); Ámsterdam, Países Bajos: ADM International; Seattle: Distribuido por University of Washington Press, 1986. ISBN 0-295-96350-6 . 

Wikimedia Commons tiene medios relacionados con Tangrams .

• Pasado y futuro: las raíces del tangram y sus desarrollos
• Cómo convertir tu juego de Tangram en un rompecabezas matemático mágico, por el diseñador de rompecabezas G. Sarcone