Dodecaedro truncado
Sólido arquimediano con 32 caras

Dodecaedro truncado
TipoSólido arquimediano
Caras32
Bordes90
Grupo de simetríasimetría icosaédrica I yo {\displaystyle \mathrm {I} _ {\mathrm {h} }}
Angulo diedro ( grados )10-10: 116,57°
3-10: 142,62°
Poliedro dualTriakis icosaedro
Figura de vértice
Neto

En geometría , el dodecaedro truncado es un sólido arquimediano . Tiene 12 caras decagonales regulares , 20 caras triangulares regulares , 60 vértices y 90 aristas.

Construcción

El dodecaedro truncado se construye a partir de un dodecaedro regular cortando todos sus vértices, un proceso conocido como truncamiento . [1] Alternativamente, el dodecaedro truncado se puede construir por expansión : alejando los bordes de un dodecaedro regular, formando las caras pentagonales en caras decagonales , así como los vértices en triángulos . [2] Por lo tanto, tiene 32 caras, 90 aristas y 60 vértices. [3]

El dodecaedro truncado también se puede construir utilizando coordenadas cartesianas . Con una longitud de arista centrada en el origen, todas son permutaciones pares de donde es la proporción áurea . [4] 2 φ − 2 {\estilo de visualización 2\varphi -2} ( 0 , ± 1 φ , ± ( 2 + φ ) ) , ( ± 1 φ , ± φ , ± 2 φ ) , ( ± φ , ± 2 , ± ( φ + 1 ) ) , {\displaystyle \left(0,\pm {\frac {1}{\varphi }},\pm (2+\varphi )\right),\qquad \left(\pm {\frac {1}{\varphi }},\pm \varphi ,\pm 2\varphi \right),\qquad \left(\pm \varphi ,\pm 2,\pm (\varphi +1)\right),} φ = 1 + 5 2 {\textstyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}

Propiedades

El área superficial y el volumen de un dodecaedro truncado de longitud de arista son: [3] A {\estilo de visualización A} V {\estilo de visualización V} a {\estilo de visualización a} A = 5 ( 3 + 6 5 + 2 5 ) a 2 ≈ 100.991 a 2 V = 5 12 ( 99 + 47 5 ) a 3 ≈ 85.040 a 3 {\displaystyle {\begin{aligned}A&=5\left({\sqrt {3}}+6{\sqrt {5+2{\sqrt {5}}}}\right)a^{2}&&\approx 100,991a^{2}\\V&={\frac {5}{12}}\left(99+47{\sqrt {5}}\right)a^{3}&&\approx 85,040a^{3}\end{aligned}}}

El ángulo diedro de un dodecaedro truncado entre dos caras dodecaédricas regulares es 116,57°, y el ángulo entre un triángulo y un dodecaedro es 142,62°. [5]

Modelo 3D de un dodecaedro truncado

El dodecaedro truncado es un sólido arquimediano , lo que significa que es un poliedro altamente simétrico y semirregular, y dos o más caras poligonales regulares diferentes se encuentran en un vértice. [6] Tiene la misma simetría que el icosaedro regular, la simetría icosaédrica . [7] Las caras poligonales que se encuentran en cada vértice son un triángulo equilátero y dos decágonos regulares, y la figura del vértice de un dodecaedro truncado es . El dual de un dodecaedro truncado es el triakisicosaedro , un sólido de Catalan , [8] que comparte la misma simetría que el dodecaedro truncado. [9] 3 ⋅ 10 2 {\displaystyle 3\cdot 10^{2}}

El dodecaedro truncado no es quiral , lo que significa que es congruente con su imagen especular. [7]

Grafo dodecaédrico truncado

La gráfica de un dodecaedro truncado

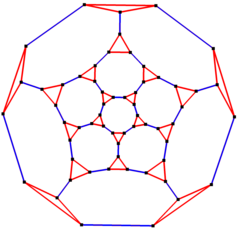
En el campo matemático de la teoría de grafos , un grafo dodecaédrico truncado es el grafo de vértices y aristas del dodecaedro truncado , uno de los sólidos arquimedianos . Tiene 60 vértices y 90 aristas, y es un grafo arquimediano cúbico . [10]

El dodecaedro truncado se puede aplicar en la construcción de poliedros conocida como aumento . Ejemplos de poliedros son los sólidos de Johnson , cuyas construcciones se realizan mediante la unión de cúpulas pentagonales sobre el dodecaedro truncado: dodecaedro truncado aumentado , dodecaedro truncado parabiaumentado , dodecaedro truncado metabiaumentado y dodecaedro truncado triaumentado . [3]

Véase también

Referencias

  1. ^ Ziya, Ümit (2019). "Espacios de dodecaedro truncado y icosaedro truncado". Revista científica Cumhuriyet . 40 (2): 457–470. doi :10.17776/csj.534616.
  2. ^ Viana, Vera; Xavier, João Pedro; Aires, Ana Paula; Campos, Helena (2019). "Expansión interactiva de poliedros aquirales". En Cocchiarella, Luigi (ed.). ICGG 2018 - Actas de la 18.ª Conferencia Internacional sobre Geometría y Gráficos: 40.º aniversario - Milán, Italia, 3-7 de agosto de 2018 . p. 1122. doi :10.1007/978-3-319-95588-9. ISBN 978-3-319-95588-9.
  3. ^ abc Berman, Martin (1971). "Poliedros convexos de caras regulares". Revista del Instituto Franklin . 291 (5): 329–352. doi :10.1016/0016-0032(71)90071-8. MR  0290245.Véase en particular la página 336.
  4. ^ Weisstein, Eric W. "Grupo icosaédrico". MathWorld .
  5. ^ Johnson, Norman W. (1966). "Poliedros convexos con caras regulares". Revista Canadiense de Matemáticas . 18 : 169–200. doi :10.4153/cjm-1966-021-8. MR  0185507. Zbl  0132.14603.
  6. ^ Diudea, MV (2018). Cúmulos poliédricos de múltiples capas. Springer . p. 39. doi :10.1007/978-3-319-64123-2. ISBN 978-3-319-64123-2.
  7. ^ ab Koca, M.; Koca, NO (2013). "Grupos de Coxeter, cuaterniones, simetrías de poliedros y politopos 4D". Física matemática: Actas de la 13.ª Conferencia regional, Antalya, Turquía, 27-31 de octubre de 2010. World Scientific. pág. 48.
  8. ^ Williams, Robert (1979). La base geométrica de la estructura natural: un libro de consulta sobre diseño. Dover Publications, Inc., pág. 88. ISBN 978-0-486-23729-9.
  9. ^ Holden, Alan (1991). Formas, espacio y simetría. Dover Books on Mathematics. Courier Corporation . pág. 52. ISBN 9780486268514.
  10. ^ Read, RC; Wilson, RJ (1998). Atlas de gráficos . Oxford University Press . pág. 269.

Lectura adicional

  • Cromwell, P. (1997). Poliedros . Reino Unido: Cambridge. pp. 79–86. Sólidos arquimedianos . ISBN . 0-521-55432-2.
  • Weisstein, Eric W. , "Dodecaedro truncado" ("Sólido arquimediano") en MathWorld .
  • Klitzing, Richard. "Poliedros uniformes convexos 3D o3x5x - tid".
  • Red editable e imprimible de un dodecaedro truncado con vista 3D interactiva
Obtenido de "https://es.wikipedia.org/w/index.php?title=Dodecaedro_truncado&oldid=1241521798"