Silogismo
Este artículo tiene varios problemas. Ayúdenos a mejorarlo o a discutir estos problemas en la página de discusión . ( Aprenda cómo y cuándo eliminar estos mensajes )
|
Un silogismo ( griego : συλλογισμός , syllogismos , 'conclusión, inferencia') es un tipo de argumento lógico que aplica el razonamiento deductivo para llegar a una conclusión basada en dos proposiciones que se afirman o se suponen como verdaderas.

En su forma más temprana (definida por Aristóteles en su libro Analíticas previas del año 350 a. C. ), un silogismo deductivo surge cuando dos premisas verdaderas (proposiciones o enunciados) implican válidamente una conclusión, o el punto principal que el argumento pretende transmitir. [1] Por ejemplo, sabiendo que todos los hombres son mortales (premisa mayor) y que Sócrates es un hombre (premisa menor), podemos concluir válidamente que Sócrates es mortal. Los argumentos silogísticos suelen representarse en forma de tres líneas:
Todos los hombres son mortales.
Sócrates es un hombre.
Por lo tanto, Sócrates es mortal. [2]
En la antigüedad existían dos teorías silogísticas rivales: el silogismo aristotélico y el silogismo estoico . [3] A partir de la Edad Media , el silogismo categórico y el silogismo se solían utilizar indistintamente. Este artículo se ocupa únicamente de este uso histórico. El silogismo estaba en el centro del razonamiento deductivo histórico, mediante el cual los hechos se determinan combinando enunciados existentes, en contraste con el razonamiento inductivo , en el que los hechos se predicen mediante observaciones repetidas.
En algunos contextos académicos, el silogismo ha sido reemplazado por la lógica de predicados de primer orden a raíz del trabajo de Gottlob Frege , en particular su Begriffsschrift ( Guión conceptual ; 1879). El silogismo, al ser un método de razonamiento lógico válido, siempre será útil en la mayoría de las circunstancias y para introducciones a la lógica y al pensamiento claro para el público en general. [4] [5]
Historia temprana
En la antigüedad existían dos teorías silogísticas rivales: el silogismo aristotélico y el silogismo estoico. [3]
Aristóteles
Aristóteles define el silogismo como "un discurso en el que habiéndose supuesto ciertas cosas (específicas), resulta necesariamente algo diferente de las cosas supuestas porque estas cosas son así". [6] A pesar de esta definición muy general, en Analíticos previos Aristóteles se limita a los silogismos categóricos que consisten en tres proposiciones categóricas , incluidos los silogismos modales categóricos . [7]
El uso de silogismos como herramienta para la comprensión se remonta a las discusiones de razonamiento lógico de Aristóteles . Antes de mediados del siglo XII, los lógicos medievales solo estaban familiarizados con una parte de las obras de Aristóteles, incluidos títulos como Categorías y Sobre la interpretación , obras que contribuyeron en gran medida a la lógica antigua predominante, o logica vetus . El surgimiento de una nueva lógica, o logica nova , surgió junto con la reaparición de Analíticos previos , la obra en la que Aristóteles desarrolló su teoría del silogismo.
Tras su redescubrimiento, los lógicos consideraron inmediatamente a la Analítica como "un cuerpo de doctrina cerrado y completo", que dejaba muy poco para que los pensadores de la época debatieran y reorganizaran. La teoría de Aristóteles sobre el silogismo para oraciones asertóricas se consideró especialmente notable, ya que solo se produjeron pequeños cambios sistemáticos en el concepto a lo largo del tiempo. Esta teoría del silogismo no entraría en el contexto de la lógica de las consecuencias, más amplia, hasta que la lógica comenzó a ser reelaborada en general a mediados del siglo XIV por personas como John Buridan .
Sin embargo, los Analíticos previos de Aristóteles no incorporaron una teoría tan completa sobre el silogismo modal, es decir, un silogismo que tiene al menos una premisa modalizada , es decir, una premisa que contiene las palabras modales necesariamente , posiblemente o contingentemente . La terminología de Aristóteles en este aspecto de su teoría fue considerada vaga y, en muchos casos, poco clara, incluso contradiciendo algunas de sus afirmaciones de Sobre la interpretación . Sus afirmaciones originales sobre este componente específico de la teoría se dejaron abiertas a una cantidad considerable de conversaciones, lo que dio lugar a una amplia gama de soluciones propuestas por los comentaristas de la época. El sistema de silogismos modales establecido por Aristóteles finalmente se consideraría inadecuado para el uso práctico y sería reemplazado por nuevas distinciones y nuevas teorías en su conjunto.
Silogismo medieval
Boecio
Boecio (c. 475-526) contribuyó a hacer más accesible la antigua lógica aristotélica. Si bien su traducción latina de Analíticas previas no se utilizó hasta el siglo XII, sus libros de texto sobre el silogismo categórico fueron fundamentales para ampliar el debate silogístico. Más que en las aportaciones que él personalmente hizo al campo, el legado lógico de Boecio reside en su transmisión eficaz de las teorías previas a los lógicos posteriores, así como en sus presentaciones claras y fundamentalmente precisas de las contribuciones de Aristóteles.
Pedro Abelardo
Otro de los primeros contribuyentes a la lógica medieval del Occidente latino, Pedro Abelardo (1079-1142), realizó su propia evaluación exhaustiva del concepto de silogismo y la teoría que lo acompañaba en la Dialectica , una discusión de la lógica basada en los comentarios y monografías de Boecio. Su perspectiva sobre los silogismos también se puede encontrar en otras obras, como Logica Ingredientibus . Con la ayuda de la distinción de Abelardo entre oraciones modales de dicto y oraciones modales de re , los lógicos medievales comenzaron a dar forma a un concepto más coherente del modelo de silogismo modal de Aristóteles.
Jean Buridán
El filósofo francés Jean Buridan (c. 1300 – 1361), a quien algunos consideran el lógico más importante de la Baja Edad Media, contribuyó con dos obras significativas: Tratado de la consecuencia y Summulae de Dialectica , en las que discutió el concepto de silogismo, sus componentes y distinciones, y las formas de usar la herramienta para expandir su capacidad lógica. Durante los 200 años posteriores a las discusiones de Buridan, se dijo poco sobre la lógica silogística. Los historiadores de la lógica han evaluado que los cambios principales en la era posterior a la Edad Media fueron cambios con respecto a la conciencia del público sobre las fuentes originales, una disminución de la apreciación por la sofisticación y complejidad de la lógica y un aumento en la ignorancia lógica, de modo que los lógicos de principios del siglo XX llegaron a ver todo el sistema como ridículo. [8]
Historia moderna
El silogismo aristotélico dominó el pensamiento filosófico occidental durante muchos siglos. El silogismo en sí mismo trata de extraer conclusiones válidas de supuestos ( axiomas ), en lugar de verificar los supuestos. Sin embargo, con el tiempo la gente se centró en el aspecto lógico, olvidando la importancia de verificar los supuestos.
En el siglo XVII, Francis Bacon enfatizó que la verificación experimental de los axiomas debe llevarse a cabo de manera rigurosa y no puede tomar el silogismo en sí mismo como la mejor manera de sacar conclusiones en la naturaleza. [9] Bacon propuso un enfoque más inductivo para la observación de la naturaleza, que involucra experimentación y conduce a descubrir y desarrollar axiomas para crear una conclusión más general. [9] Sin embargo, un método completo para sacar conclusiones en la naturaleza no es el alcance de la lógica o el silogismo, y el método inductivo fue cubierto en el tratado posterior de Aristóteles, los Analíticos posteriores .
En el siglo XIX, se incorporaron modificaciones al silogismo para abordar los enunciados disyuntivos ("A o B") y condicionales ("si A entonces B"). Immanuel Kant afirmó en su famosa obra Lógica (1800) que la lógica era la única ciencia completa y que la lógica aristotélica incluía más o menos todo lo que había que saber sobre la lógica (esta obra no es necesariamente representativa de la filosofía madura de Kant, que a menudo se considera una innovación de la lógica misma). La opinión de Kant no fue cuestionada en Occidente hasta 1879, cuando Gottlob Frege publicó su Begriffsschrift ( Escritor de conceptos ), que introdujo un cálculo, un método para representar enunciados categóricos (y también enunciados que no están previstos en el silogismo) mediante el uso de cuantificadores y variables.
Una notable excepción es la lógica desarrollada en la obra de Bernard Bolzano Wissenschaftslehre ( Teoría de la ciencia , 1837), cuyos principios fueron aplicados como una crítica directa de Kant, en la obra publicada póstumamente Nuevo anti-Kant (1850). La obra de Bolzano había sido en gran medida ignorada hasta finales del siglo XX, entre otras razones, debido al ambiente intelectual de la época en Bohemia , que entonces formaba parte del Imperio austríaco . En los últimos 20 años, la obra de Bolzano ha resurgido y se ha convertido en tema tanto de traducción como de estudio contemporáneo.
Esto condujo al rápido desarrollo de la lógica oracional y la lógica de predicados de primer orden , subsumiendo el razonamiento silogístico, que, por lo tanto, después de 2000 años, de repente fue considerado obsoleto por muchos. [ investigación original? ] El sistema aristotélico se explica en los foros académicos modernos principalmente en material introductorio y estudio histórico.
Una notable excepción a esta relegación moderna es la continua aplicación de la lógica aristotélica por parte de los funcionarios de la Congregación para la Doctrina de la Fe y el Tribunal Apostólico de la Rota Romana , que todavía requiere que cualquier argumento elaborado por los abogados se presente en formato silogístico.
La aceptación de Aristóteles por parte de Boole
La aceptación inquebrantable de George Boole de la lógica de Aristóteles es enfatizada por el historiador de la lógica John Corcoran en una introducción accesible a Laws of Thought . [10] [11] Corcoran también escribió una comparación punto por punto de Prior Analytics y Laws of Thought . [12] Según Corcoran, Boole aceptó y respaldó plenamente la lógica de Aristóteles. Los objetivos de Boole eran "ir por debajo, por encima y más allá" de la lógica de Aristóteles mediante: [12]
- dotándola de fundamentos matemáticos que impliquen ecuaciones;
- ampliar la clase de problemas que podría tratar, ya que se agregó la resolución de ecuaciones para evaluar la validez ; y
- ampliando la gama de aplicaciones que podría manejar, como por ejemplo ampliar proposiciones de sólo dos términos a aquellas que tienen un número arbitrario de ellos.
Más específicamente, Boole estaba de acuerdo con lo que decía Aristóteles ; los «desacuerdos» de Boole, si se los puede llamar así, se refieren a lo que Aristóteles no dijo. En primer lugar, en el ámbito de los fundamentos, Boole redujo las cuatro formas proposicionales de Aristóteles a una sola forma, la forma de las ecuaciones, lo que en sí mismo era una idea revolucionaria. En segundo lugar, en el ámbito de los problemas de la lógica, la adición de Boole de la resolución de ecuaciones a la lógica (otra idea revolucionaria) implicaba la doctrina de Boole de que las reglas de inferencia de Aristóteles (los «silogismos perfectos») deben complementarse con reglas para la resolución de ecuaciones. En tercer lugar, en el ámbito de las aplicaciones, el sistema de Boole podía manejar proposiciones y argumentos de múltiples términos, mientras que Aristóteles sólo podía manejar proposiciones y argumentos de sujeto-predicado de dos términos. Por ejemplo, el sistema de Aristóteles no podía deducir: “Ningún cuadrángulo que sea un cuadrado es un rectángulo que sea un rombo” de “Ningún cuadrado que sea un cuadrángulo es un rombo que sea un rectángulo” o de “Ningún rombo que sea un rectángulo es un cuadrado que sea un cuadrángulo”.
Estructura básica
Un silogismo categórico consta de tres partes:
- Premisa mayor
- Premisa menor
- Conclusión/Consecuencia
Cada parte es una proposición categórica , y cada proposición categórica contiene dos términos categóricos. [13] En Aristóteles, cada una de las premisas está en la forma "Todos los S son P", "Algunos S son P", "Ningún S es P" o "Algunos S no son P", donde "S" es el término sujeto y "P" es el término predicado:
- "Todos los S son P" y "Ningún S es P" se denominan proposiciones universales ;
- "Algunos S son P" y "Algunos S no son P" se denominan proposiciones particulares .
Los lógicos más modernos permiten algunas variaciones. Cada una de las premisas tiene un término en común con la conclusión: en una premisa mayor, este es el término mayor (es decir, el predicado de la conclusión); en una premisa menor, este es el término menor (es decir, el sujeto de la conclusión). Por ejemplo:
- Premisa mayor : Todos los humanos son mortales.
- Premisa menor : Todos los griegos son humanos.
- Conclusión/Consecuente : Todos los griegos son mortales.
Cada uno de los tres términos distintos representa una categoría. En el ejemplo anterior, humanos , mortal y griegos : mortal es el término principal y griegos el término secundario. Las premisas también tienen un término en común entre sí, que se conoce como término medio ; en este ejemplo, humanos . Ambas premisas son universales, al igual que la conclusión.
- Premisa mayor : Todos los mortales mueren.
- Premisa menor : Todos los hombres son mortales.
- Conclusión/Consecuente : Todos los hombres mueren.
Aquí, el término mayor es morir , el término menor es hombres y el término medio es mortales . Nuevamente, ambas premisas son universales, por lo tanto, también lo es la conclusión.
Polisilogismo
Un polisilogismo, o sorites , es una forma de argumentación en la que una serie de silogismos incompletos se organiza de tal manera que el predicado de cada premisa forma el sujeto de la siguiente hasta que el sujeto de la primera se une con el predicado de la última en la conclusión. Por ejemplo, se podría argumentar que todos los leones son grandes felinos, todos los grandes felinos son depredadores y todos los depredadores son carnívoros. Concluir que, por lo tanto, todos los leones son carnívoros es construir un argumento sorites.
Tipos
Es posible que esta sección contenga investigaciones originales . ( Julio de 2020 ) |

(las áreas negras están vacías,
las áreas rojas no están vacías).
Hay una infinidad de silogismos posibles, pero sólo 256 tipos lógicamente distintos y sólo 24 tipos válidos (enumerados a continuación). Un silogismo adopta la forma (nota: M – medio, S – sujeto, P – predicado):
- Premisa mayor : Todos los M son P.
- Premisa menor : Todos los S son M.
- Conclusión/Consecuente : Todas las S son P.
Las premisas y la conclusión de un silogismo pueden ser de cuatro tipos, que se identifican con letras [14] de la siguiente manera. El significado de las letras se indica en la tabla:
| código | cuantificador | sujeto | cópula | predicado | tipo | ejemplo |
|---|---|---|---|---|---|---|
| A | Todo | S | son | PAG | afirmativa universal | Todos los humanos son mortales. |
| mi | No | S | son | PAG | negativo universal | Ningún ser humano es perfecto. |
| I | Alguno | S | son | PAG | afirmativa particular | Algunos humanos están sanos. |
| Oh | Alguno | S | no son | PAG | Particularmente negativo | Algunos humanos no son viejos. |
En Analítica previa , Aristóteles utiliza principalmente las letras A, B y C (letras griegas alpha , beta y gamma ) como marcadores de posición de términos, en lugar de dar ejemplos concretos. Es tradicional utilizar is en lugar de are como cópula , por lo tanto All A is B en lugar de All A are Bs . Es una práctica tradicional y conveniente utilizar a, e, i, o como operadores infijos para que las declaraciones categóricas se puedan escribir de forma sucinta. La siguiente tabla muestra la forma más larga, la forma abreviada sucinta y las expresiones equivalentes en lógica de predicados:
| Forma | Taquigrafía | Lógica de predicados |
|---|---|---|
| Todo A es B | AaB | o |
| No A es B | AEB | o |
| Alguna A es B | AiB | |
| Alguna A no es B | Cualquier otro negocio |
La convención aquí es que la letra S es el sujeto de la conclusión, P es el predicado de la conclusión y M es el término medio. La premisa mayor vincula M con P y la premisa menor vincula M con S. Sin embargo, el término medio puede ser el sujeto o el predicado de cada premisa donde aparece. Las diferentes posiciones de los términos mayor, menor y medio dan lugar a otra clasificación de silogismos conocida como figura . Dado que en cada caso la conclusión es SP, las cuatro figuras son:
| Figura 1 | Figura 2 | Figura 3 | Figura 4 | |
|---|---|---|---|---|
| Premisa mayor | M-P | P.M | M-P | P.M |
| Premisa menor | S-M | S-M | EM | EM |
(Nótese, sin embargo, que, siguiendo el tratamiento de las figuras por parte de Aristóteles, algunos lógicos (por ejemplo, Peter Abelard y Jean Buridan) rechazan la cuarta figura como una figura distinta de la primera.)
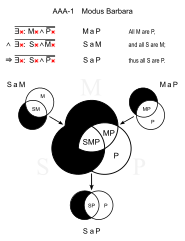
Si sumamos todo, hay 256 tipos posibles de silogismos (o 512 si se cambia el orden de las premisas mayores y menores, aunque esto no supone ninguna diferencia lógica). Cada premisa y conclusión pueden ser del tipo A, E, I u O, y el silogismo puede ser cualquiera de las cuatro figuras. Un silogismo se puede describir brevemente dando las letras de las premisas y la conclusión seguidas del número de la figura. Por ejemplo, el silogismo BARBARA que aparece a continuación es AAA-1, o "AAA en la primera figura".
La gran mayoría de las 256 formas posibles de silogismo son inválidas (la conclusión no se sigue lógicamente de las premisas). La siguiente tabla muestra las formas válidas. Incluso algunas de ellas a veces se considera que cometen la falacia existencial , lo que significa que son inválidas si mencionan una categoría vacía. Estos patrones controvertidos están marcados en cursiva . Todos menos cuatro de los patrones en cursiva (felapton, darapti, fesapo y bamalip) son modos debilitados, es decir, es posible extraer una conclusión más fuerte de las premisas.
| Figura 1 | Figura 2 | Figura 3 | Figura 4 |
|---|---|---|---|
| Bárbara | César | D a t i s i | C a l e m e s |
| C e l a r e n t | Came estresa | Disamís | Dimátis |
| D a r ii | Fiesta | Ferison | Frescura |
| Frío | Barroco | Bocard o | C a l e m o s |
| Bárbara | César | Felaptón | Fésapo |
| C e l a r o n t | Caméstros | D a r a pt i | B a m a l i p |
Las letras A, E, I y O se han utilizado desde las escuelas medievales para formar nombres mnemotécnicos para las formas como sigue: 'Barbara' significa AAA, 'Celarent' significa EAE, etc.
Junto a cada premisa y conclusión hay una descripción abreviada de la oración. Así, en AAI-3, la premisa "Todos los cuadrados son rectángulos" se convierte en "MaP"; los símbolos significan que el primer término ("cuadrado") es el término intermedio, el segundo término ("rectángulo") es el predicado de la conclusión y la relación entre los dos términos se etiqueta como "a" (Todos los M son P).
La siguiente tabla muestra todos los silogismos que son esencialmente diferentes. Los silogismos similares comparten las mismas premisas, solo que escritas de forma diferente. Por ejemplo, "Algunas mascotas son gatitos" (SiM en darii) también podría escribirse como "Algunas mascotas son gatitos" (MiS en datisi).
En los diagramas de Venn, las áreas negras indican que no hay elementos y las áreas rojas indican que hay al menos un elemento. En las expresiones de lógica de predicados, una barra horizontal sobre una expresión significa negar ("no lógico") el resultado de esa expresión.
También es posible utilizar gráficos (que consisten en vértices y aristas) para evaluar silogismos. [15]
Ejemplos
 |  |
| M: hombres S: griegos P: mortales |
Bárbara (AAA-1)
- Todos los hombres son mortales. (MaP)
- Todos los griegos son hombres. (SaM)
- ∴ Todos los griegos son mortales. (SaP)
 |  |
| M: reptil S: serpiente P: pelaje |
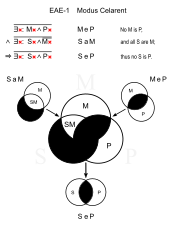
Celarente (EAE-1)
Similares: Cesare (EAE-2)
- Ningún reptil tiene pelo. (MeP)
- Todas las serpientes son reptiles. (SaM)
- ∴ Ninguna serpiente tiene pelo. (SeP)
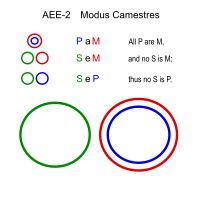
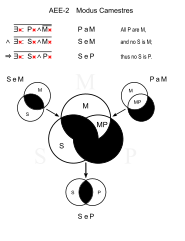
| Camestres (AEE-2) | |||
|---|---|---|---|
Camestres es básicamente como Celarent con S y P intercambiados.
|
 |  |
| M: conejo S: mascota P: pelaje |
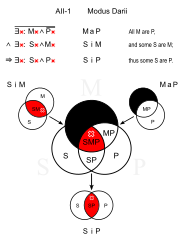
Darií (AII-1)
Similares: Datisi (AII-3)
- Todos los conejos tienen pelo. (MaP)
- Algunas mascotas son conejos. (SiM)
- ∴ Algunas mascotas tienen pelo. (SiP)
| Disamis (IAI-3) | |||
|---|---|---|---|
Disamis es básicamente como Darii con S y P intercambiados.
|
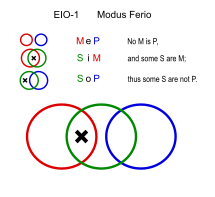 |  |
| M: tarea S: lectura P: diversión |
Ferio (EIO-1)
Similares: Festino (EIO-2), Ferison (EIO-3), Fresison (EIO-4)
- Ninguna tarea es divertida. (MeP)
- Algunas lecturas son tarea para hacer en casa. (SiM)
- ∴ Algunas lecturas no son divertidas. (SoP)
 |  |
| M: mamífero S: mascota P: gato |
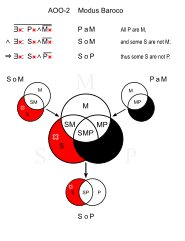
Barroco (AOO-2)
- Todos los gatos son mamíferos. (PaM)
- Algunas mascotas no son mamíferos. (SoM)
- ∴ Algunas mascotas no son gatos. (SoP)
 |  |
| M: gato S: mamífero P: mascota |
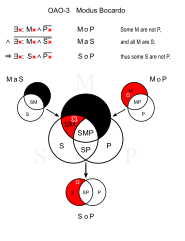
Bocardo (OAO-3)
- Algunos gatos no son mascotas. (MoP)
- Todos los gatos son mamíferos. (MaS)
- ∴ Algunos mamíferos no son mascotas. (SoP)
 |  |
| M: hombre S: griego P: mortal |
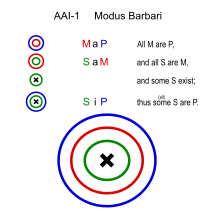
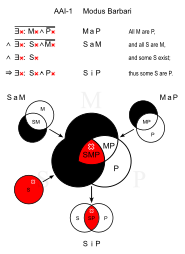
Bárbaro (AAI-1)
- Todos los hombres son mortales. (MaP)
- Todos los griegos son hombres. (SaM)
- ∴ Algunos griegos son mortales. (SiP)
| Bamalip (AAI-4) | |||
|---|---|---|---|
Bamalip es exactamente igual que Barbari con S y P intercambiados:
|
 |  |
| M: reptil S: serpiente P: pelaje |
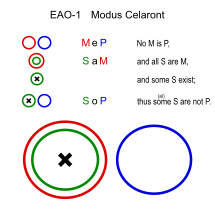
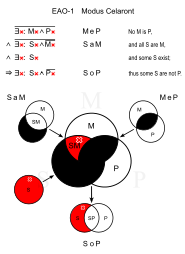
Celaronte (EAO-1)
Similares: Cesaro (EAO-2)
- Ningún reptil tiene pelo. (MeP)
- Todas las serpientes son reptiles. (SaM)
- ∴ Algunas serpientes no tienen pelo. (SoP)
 |  |
| M: pezuñas S: humano P: caballo |
Camestros (AEO-2)
Similares: Calemos (AEO-4)
- Todos los caballos tienen pezuñas. (PaM)
- Ningún ser humano tiene pezuñas. (SeM)
- ∴ Algunos humanos no son caballos. (SoP)
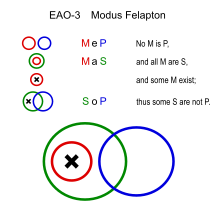 |  |
| M: flor S: planta P: animal |
Felaptón (EAO-3)
Similares: Fesapo (EAO-4)
- Ninguna flor es un animal. (MeP)
- Todas las flores son plantas. (MaS)
- ∴ Algunas plantas no son animales. (SoP)
 |  |
| M: cuadrado S: rombo P: rectángulo |
Darapti (AAI-3)
- Todos los cuadrados son rectángulos . (MaP)
- Todos los cuadrados son rombos . (MaS)
- ∴ Algunos rombos son rectángulos. (SiP)
Tabla de todos los silogismos
Esta tabla muestra los 24 silogismos válidos, representados por diagramas de Venn . Las columnas indican similitud y están agrupadas por combinaciones de premisas. Los bordes corresponden a conclusiones. Las que tienen un supuesto existencial están en línea discontinua.
Términos en silogismo
This section has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
Con Aristóteles, podemos distinguir términos singulares , como Sócrates , y términos generales, como Griegos . Aristóteles distinguió además los tipos (a) y (b):
- términos que podrían ser objeto de predicación; y
- términos que podrían predicarse de otros mediante el uso de la cópula ("es un").
Tal predicación se conoce como distributiva , en oposición a no distributiva como en Los griegos son numerosos . Está claro que el silogismo de Aristóteles funciona solo para la predicación distributiva, ya que no podemos razonar Todos los griegos son animales, los animales son numerosos, por lo tanto, todos los griegos son numerosos . En opinión de Aristóteles, los términos singulares eran del tipo (a) y los términos generales del tipo (b). Por lo tanto, los hombres pueden predicarse de Sócrates , pero Sócrates no puede predicarse de nada. Por lo tanto, para que un término sea intercambiable (es decir, que esté en la posición de sujeto o predicado de una proposición en un silogismo), los términos deben ser términos generales, o términos categóricos, como se los llamó. En consecuencia, las proposiciones de un silogismo deben ser proposiciones categóricas (ambos términos generales) y los silogismos que emplean solo términos categóricos pasaron a llamarse silogismos categóricos .
Está claro que nada impediría que un término singular apareciera en un silogismo, siempre que estuviera siempre en la posición del sujeto; sin embargo, tal silogismo, incluso si fuera válido, no es un silogismo categórico. Un ejemplo es Sócrates es un hombre, todos los hombres son mortales, por lo tanto, Sócrates es mortal. Intuitivamente, esto es tan válido como Todos los griegos son hombres, todos los hombres son mortales, por lo tanto, todos los griegos son mortales . Argumentar que su validez puede explicarse por la teoría del silogismo requeriría que mostráramos que Sócrates es un hombre es el equivalente de una proposición categórica. Se puede argumentar que Sócrates es un hombre es equivalente a Todos los que son idénticos a Sócrates son hombres , por lo que nuestro silogismo no categórico puede justificarse mediante el uso de la equivalencia anterior y luego citando a BARBARA.
Importancia existencial
This section has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
Si un enunciado incluye un término tal que el enunciado es falso si el término no tiene instancias, entonces se dice que el enunciado tiene importancia existencial con respecto a ese término. Es ambiguo si un enunciado universal de la forma Todo A es B debe considerarse verdadero, falso o incluso carente de sentido si no hay A. Si se considera falso en tales casos, entonces el enunciado Todo A es B tiene importancia existencial con respecto a A.
Se afirma que el sistema lógico de Aristóteles no cubre casos en los que no existen instancias. El objetivo de Aristóteles era desarrollar una lógica para la ciencia. Relega ficciones como las sirenas y los unicornios al ámbito de la poesía y la literatura. En su mente, existen fuera del ámbito de la ciencia, por lo que no deja lugar para esas entidades inexistentes en su lógica. Esta es una elección meditada, no una omisión involuntaria. Técnicamente, la ciencia aristotélica es una búsqueda de definiciones, donde una definición es "una frase que significa la esencia de una cosa". Como las entidades inexistentes no pueden ser nada, en la mente de Aristóteles no poseen una esencia. Es por eso que no deja lugar para entidades ficticias como los ciervos-cabra (o los unicornios). [16]
Sin embargo, muchos sistemas lógicos desarrollados desde entonces sí consideran el caso en el que puede no haber instancias. Los lógicos medievales eran conscientes del problema del significado existencial y sostenían que las proposiciones negativas no tienen significado existencial y que las proposiciones positivas con sujetos que no suponen son falsas.
Surgen los siguientes problemas:
- En el lenguaje natural y el uso normal, ¿qué enunciados de las formas Todo A es B, Ningún A es B, Algún A es B y Algún A no es B tienen importancia existencial y con respecto a qué términos?
- En las cuatro formas de enunciados categóricos utilizados en el silogismo, ¿qué enunciados de la forma AaB, AeB, AiB y AoB tienen importancia existencial y con respecto a qué términos?
- ¿Qué implicaciones existenciales deben tener las formas AaB, AeB, AiB y AoB para que el cuadrado de oposición sea válido?
- ¿Qué implicaciones existenciales deben tener las formas AaB, AeB, AiB y AoB para preservar la validez de las formas tradicionalmente válidas de los silogismos?
- ¿Son las importaciones existenciales requeridas para satisfacer (d) anterior tales que los usos normales en lenguajes naturales de las formas Todo A es B, Ningún A es B, Algún A es B y Algún A no es B se reflejan intuitiva y justamente en los enunciados categóricos de las formas AaB, AeB, AiB y AoB?
Por ejemplo, si se acepta que AiB es falso si no hay As y AaB implica AiB, entonces AiB tiene importancia existencial con respecto a A, y también AaB. Además, si se acepta que AiB implica BiA, entonces AiB y AaB tienen importancia existencial con respecto a B también. De manera similar, si AoB es falso si no hay As, y AeB implica AoB, y AeB implica BeA (que a su vez implica BoA), entonces tanto AeB como AoB tienen importancia existencial con respecto a A y B. De ello se sigue inmediatamente que todos los enunciados categóricos universales tienen importancia existencial con respecto a ambos términos. Si AaB y AeB son una representación justa del uso de enunciados en lenguaje natural normal de Todo A es B y Ningún A es B respectivamente, entonces surgen las siguientes consecuencias de ejemplo:
- "Todos los caballos voladores son míticos" es falso si no existen caballos voladores.
- Si "Ningún hombre es conejo come fuego" es verdadero, entonces "Hay conejos come fuego" es verdadero; y así sucesivamente.
Si se decide que ningún enunciado universal tiene importancia existencial, entonces el cuadrado de oposición falla en varios aspectos (por ejemplo, AaB no implica AiB) y varios silogismos ya no son válidos (por ejemplo, BaC, AaB -> AiC).
Estos problemas y paradojas surgen tanto en los enunciados en lenguaje natural como en los enunciados en forma de silogismo debido a la ambigüedad, en particular la ambigüedad con respecto a Todo. Si "Fred afirma que todos sus libros ganaron el Premio Pulitzer", ¿está Fred afirmando que escribió algún libro? Si no, ¿es cierto lo que afirma? Supongamos que Jane dice que ninguno de sus amigos es pobre; ¿es eso cierto si no tiene amigos?
El cálculo de predicados de primer orden evita tal ambigüedad al usar fórmulas que no tienen importancia existencial con respecto a enunciados universales. Las afirmaciones existenciales deben enunciarse explícitamente. Por lo tanto, los enunciados en lenguaje natural (de las formas Todo A es B, Ningún A es B , Algún A es B y Algún A no es B) pueden representarse en el cálculo de predicados de primer orden en el que cualquier importancia existencial con respecto a los términos A y/o B es explícita o no se hace en absoluto. En consecuencia, las cuatro formas AaB, AeB, AiB y AoB pueden representarse en el predicado de primer orden en cada combinación de importancia existencial, de modo que puede establecer qué interpretación, si la hay, preserva el cuadrado de oposición y la validez del silogismo tradicionalmente válido. Strawson afirma que tal interpretación es posible, pero los resultados son tales que, en su opinión, la respuesta a la pregunta (e) anterior es no .
Falacias silogísticas
La gente a menudo comete errores al razonar silogísticamente. [17]
Por ejemplo, a partir de las premisas algunos A son B, algunos B son C, la gente tiende a llegar a una conclusión definitiva de que, por lo tanto, algunos A son C. [18] [19] Sin embargo, esto no se sigue de acuerdo con las reglas de la lógica clásica. Por ejemplo, mientras que algunos gatos (A) son cosas negras (B), y algunas cosas negras (B) son televisores (C), no se sigue de los parámetros que algunos gatos (A) sean televisores (C). Esto se debe a que en la estructura del silogismo invocado (es decir, III-1) el término medio no está distribuido ni en la premisa mayor ni en la premisa menor, un patrón llamado la " falacia del término medio no distribuido ". Debido a esto, puede ser difícil seguir la lógica formal, y se necesita una mirada más atenta para garantizar que un argumento sea, de hecho, válido. [20]
Para determinar la validez de un silogismo es necesario determinar la distribución de cada término en cada enunciado, es decir, si se tienen en cuenta todos los miembros de ese término.
En patrones silogísticos simples, las falacias de patrones inválidos son:
- Medio no distribuido : Ninguna de las premisas da cuenta de todos los miembros del término medio, lo que en consecuencia no logra vincular el término mayor y el menor.
- Tratamiento ilícito del término mayor : la conclusión implica a todos los miembros del término mayor (P – lo que significa que la proposición es negativa); sin embargo, la premisa mayor no los da cuenta a todos (es decir, P es un predicado afirmativo o un sujeto particular allí).
- Tratamiento ilícito del término menor : Igual que el anterior, pero para el término menor (S – lo que significa que la proposición es universal) y la premisa menor (donde S es un sujeto particular o un predicado afirmativo).
- Premisas excluyentes : Ambas premisas son negativas, es decir, no se establece ningún vínculo entre los términos mayores y menores.
- Conclusión afirmativa de una premisa negativa : si alguna de las premisas es negativa, la conclusión también debe serlo.
- Conclusión negativa de premisas afirmativas : Si ambas premisas son afirmativas, la conclusión también debe serlo.
Otros tipos
- Silogismo disyuntivo
- Silogismo hipotético
- Silogismo jurídico
- Polisilogismo
- Silogismo prosléptico
- Cuasi-silogismo
- Silogismo estadístico
Véase también
- Falacia silogística
- Teoría de la argumentación
- Lógica budista
- Entimema
- Falacia formal
- Falacia lógica
- La falsa sutileza de las cuatro figuras silogísticas
- Tautología (lógica)
- Diagrama de Venn
Referencias
- ^ Lundberg, Christian (2018). La guía esencial de la retórica . Bedford/St. Martin's. pág. 38.
- ^ John Stuart Mill, Un sistema de lógica, raciocinativa e inductiva, siendo una visión conectada de los principios de la evidencia y los métodos de investigación científica , 3.ª ed., vol. 1, cap. 2 (Londres: John W. Parker, 1851), 190.
- ^ ab Frede, Michael . 1975. "Estoico vs. Silogismo peripatético". Archivo para la Historia de la Filosofía 56:99–124.
- ^ Hurley, Patrick J. 2011. Una breve introducción a la lógica . Cengage Learning. ISBN 9780840034175
- ^ Zegarelli, Mark. 2010. Lógica para tontos . John Wiley & Sons. ISBN 9781118053072 .
- ^ Aristóteles , Analíticos previos , 24b18–20
- ^ Bobzien, Susanne . [2006] 2020. "Lógica antigua". Enciclopedia de Filosofía de Stanford . § Aristóteles.
- ^ Lagerlund, Henrik (2 de febrero de 2004). «Teorías medievales del silogismo». The Stanford Encyclopedia of Philosophy . Edward N. Zalta . Consultado el 17 de febrero de 2014 .
- ^ ab Bacon, Francis . [1620] 2001. La Gran Instauración . – vía Constitution Society . Archivado desde el original el 13 de abril de 2019.
- ^ Boole, George . [1854] 2003. Las leyes del pensamiento , con una introducción de J. Corcoran. Buffalo: Prometheus Books .
- ^ van Evra, James. 2004. "'Las leyes del pensamiento' de George Boole" (reseña). Philosophy in Review 24:167–69.
- ^ ab Corcoran, John . 2003. "Los 'Prior Analíticos' de Aristóteles y las 'Leyes del Pensamiento' de Boole". Historia y Filosofía de la Lógica 24:261–88.
- ^ "Diccionario filosófico: Caird-Catharsis". Philosophypages.com. 8 de agosto de 2002. Consultado el 14 de diciembre de 2009 .
- ^ Según Copi , p. 127: 'Se presume que los nombres de las letras provienen de las palabras latinas " A ff I rmo" y "n E g O ", que significan "afirmo" y "niego", respectivamente; la primera letra mayúscula de cada palabra es para universal, la segunda para particular'
- ^ "Silogismos simplificados". Archivado desde el original el 11 de diciembre de 2021 – vía www.youtube.com.
- ^ "Groarke, Louis F., "Aristóteles: Lógica", sección 7. (Supuestos existenciales), Internet Encyclopedia of Philosophy". Archivado desde el original el 4 de febrero de 2017. Consultado el 7 de marzo de 2017 .
- ^ Véase, por ejemplo, Evans, J. St. B. T (1989). Sesgo en el razonamiento humano . Londres: LEA.
- ^ Khemlani, S. y PN Johnson-Laird. 2012. "Teorías del silogismo: un metaanálisis". Psychological Bulletin 138:427–57.
- ^ Chater, N. y M. Oaksford. 1999. "El modelo heurístico de probabilidad del razonamiento silogístico". Psicología cognitiva 38:191–258.
- ^ Lundberg, Christian (2018). La guía esencial de la retórica . Bedford/St. Martin's. pág. 39.
Fuentes
- Aristóteles , [c. 350 a. C.] 1989. Analíticas previas , traducidas por R. Smith. Hackett. ISBN 0-87220-064-7
- Blackburn, Simon . [1994] 1996. "Silogismo". En The Oxford Dictionary of Philosophy . Oxford University Press. ISBN 0-19-283134-8 .
- Broadie, Alexander. 1993. Introducción a la lógica medieval . Oxford University Press. ISBN 0-19-824026-0 .
- Copi, Irving . 1969. Introducción a la lógica (3.ª ed.). Macmillan Company.
- Corcoran, John . 1972. "Completitud de una lógica antigua". Journal of Symbolic Logic 37:696–702.
- — 1994. “La fundación de la lógica: interpretaciones modernas de la lógica de Aristóteles”. Filosofía antigua 14:9–24.
- Corcoran, John y Hassan Masoud. 2015. "Importancia existencial hoy: nuevos metateoremas; conceptos erróneos históricos, filosóficos y pedagógicos". Historia y filosofía de la lógica 36(1):39–61.
- Englebretsen, George. 1987. La Nueva Silogística . Berna: Peter Lang .
- Hamblin, Charles Leonard . 1970. Falacias . Londres: Methuen . ISBN 0-416-70070-5 .
- Cf. sobre la validez de los silogismos: "Un conjunto simple de reglas de validez fue finalmente producido en la Baja Edad Media, basado en el concepto de Distribución".
- Łukasiewicz, Jan. [1957] 1987. La silogística de Aristóteles desde el punto de vista de la lógica formal moderna . Nueva York: Garland Publishers. ISBN 0-8240-6924-2 . OCLC 15015545.
- Malink, Marko. 2013. La silogística modal de Aristóteles . Cambridge, MA: Harvard University Press .
- Patzig, Günter. 1968. La teoría aristotélica del silogismo: un estudio lógico-filológico del Libro A de los Analíticos Primeros . Dordrecht: Reidel.
- Rescher, Nicholas. 1966. Galeno y el silogismo . University of Pittsburgh Press. ISBN 978-0822983958 .
- Smiley, Timothy . 1973. "¿Qué es un silogismo?" Revista de lógica filosófica 2:136–54.
- Smith, Robin. 1986. "Proposiciones inmediatas y teoría de la prueba de Aristóteles". Filosofía antigua 6:47–68.
- Thom, Paul. 1981. "El silogismo". Philosophia . Múnich. ISBN 3-88405-002-8 .
Enlaces externos
- Smith, Robin. "La lógica de Aristóteles". En Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy .
- Koutsoukou-Argyraki, Angeliki. La silogística asertórica de Aristóteles (Desarrollo de pruebas formales en Isabelle/HOL, Archive of Formal Proofs)
- Lagerlund, Henrik. "Teorías medievales del silogismo". En Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy .
- Analíticas previas de Aristóteles: la teoría del silogismo categórico una bibliografía comentada sobre la teoría silogística de Aristóteles
- Sistema silogístico difuso
- Desarrollo de algoritmos silogísticos difusos y aplicaciones Enfoques de razonamiento distribuido
- Comparación entre el silogismo aristotélico y el silogismo indio/tibetano
- La filosofía budista del flujo universal (Capítulo XXIII – Miembros de un silogismo (avayava))
- Máquina silogística en línea Una máquina silogística interactiva para explorar todas las falacias, figuras, términos y modos de los silogismos.