Autómata de sufijo
| Autómata de sufijo | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 | |||||||||||||||
| Tipo | Índice de subcadena | ||||||||||||||
| Inventado | 1983 | ||||||||||||||
| Inventado por | Anselmo Blumer; Janet Blumer; Andrzej Ehrenfeucht ; David Haussler ; Ross McConnell | ||||||||||||||
| |||||||||||||||
En informática , un autómata de sufijo es una estructura de datos eficiente para representar el índice de subcadena de una cadena dada que permite el almacenamiento, procesamiento y recuperación de información comprimida sobre todas sus subcadenas . El autómata de sufijo de una cadena es el grafo acíclico dirigido más pequeño con un vértice inicial dedicado y un conjunto de vértices "finales", de modo que las rutas desde el vértice inicial hasta los vértices finales representan los sufijos de la cadena.
En términos de la teoría de autómatas , un autómata de sufijo es el autómata finito determinista parcial mínimo que reconoce el conjunto de sufijos de una cadena dada . El gráfico de estados de un autómata de sufijo se denomina gráfico de palabras acíclico dirigido (DAWG), un término que también se utiliza a veces para cualquier autómata de estado finito acíclico determinista .
Los autómatas de sufijo fueron introducidos en 1983 por un grupo de científicos de la Universidad de Denver y la Universidad de Colorado en Boulder . Sugirieron un algoritmo en línea de tiempo lineal para su construcción y demostraron que el autómata de sufijo de una cadena con una longitud de al menos dos caracteres tiene como máximo estados y como máximo transiciones. Trabajos posteriores han demostrado una estrecha conexión entre los autómatas de sufijo y los árboles de sufijo , y han esbozado varias generalizaciones de los autómatas de sufijo, como el autómata de sufijo compactado obtenido por compresión de nodos con un único arco saliente.
Los autómatas de sufijo proporcionan soluciones eficientes a problemas como la búsqueda de subcadenas y el cálculo de la subcadena común más grande de dos o más cadenas.
Historia

El concepto de autómata de sufijo fue introducido en 1983 [1] por un grupo de científicos de la Universidad de Denver y la Universidad de Colorado en Boulder formado por Anselm Blumer, Janet Blumer, Andrzej Ehrenfeucht , David Haussler y Ross McConnell, aunque conceptos similares se habían estudiado anteriormente junto con árboles de sufijos en los trabajos de Peter Weiner, [2] Vaughan Pratt [3] y Anatol Slissenko . [4] En su trabajo inicial, Blumer et al . mostraron un autómata de sufijo construido para la cadena de longitud mayor que tiene en la mayoría de los estados y en la mayoría de las transiciones, y sugirieron un algoritmo lineal para la construcción de autómatas. [5]
En 1983, Mu-Tian Chen y Joel Seiferas demostraron de forma independiente que el algoritmo de construcción de árboles de sufijos de Weiner de 1973 [2], al construir un árbol de sufijos de la cadena, construye un autómata de sufijos de la cadena invertida como estructura auxiliar. [6] En 1987, Blumer et al . aplicaron la técnica de compresión utilizada en árboles de sufijos a un autómata de sufijos e inventaron el autómata de sufijos compactado, que también se denomina gráfico de palabras acíclico dirigido compactado (CDAWG). [7] En 1997, Maxime Crochemore y Renaud Vérin desarrollaron un algoritmo lineal para la construcción directa de CDAWG. [1] En 2001, Shunsuke Inenaga et al . desarrollaron un algoritmo para la construcción de CDAWG para un conjunto de palabras dado por un trie . [8]
Definiciones
Generalmente, cuando se habla de autómatas sufijos y conceptos relacionados, se utilizan algunas nociones de la teoría del lenguaje formal y de la teoría de autómatas , en particular: [9]
- El "alfabeto" es un conjunto finito que se utiliza para construir palabras. Sus elementos se denominan "caracteres";
- "Palabra" es una secuencia finita de caracteres . La "longitud" de la palabra se denota como ;
- " Lenguaje formal " es un conjunto de palabras sobre un alfabeto determinado;
- "El lenguaje de todas las palabras" se denota con el carácter (donde el carácter "*" representa la estrella de Kleene ), "palabra vacía" (la palabra de longitud cero) se denota con el carácter ;
- " Concatenación de palabras" y se denota como o y corresponde a la palabra que se obtiene al escribir a la derecha de , es decir, ;
- "Concatenación de idiomas" y se denota como o y corresponde al conjunto de concatenaciones por pares ;
- Si la palabra puede representarse como , donde , entonces las palabras , y se denominan "prefijo", "sufijo" y " subpalabra " (subcadena) de la palabra correspondientemente;
- Si y (con ) entonces se dice que "ocurre" en como subpalabra. Aquí y se denominan posiciones izquierda y derecha de ocurrencia de en correspondientemente.
Estructura del autómata
Formalmente, el autómata finito determinista está determinado por 5-tuplas , donde: [10]
- es un "alfabeto" que se utiliza para construir palabras,
- es un conjunto de " estados " del autómata,
- es un estado "inicial" del autómata,
- es un conjunto de estados "finales" del autómata,
- es una función de "transición" parcial del autómata, de modo que para y no está definido o define una transición desde sobre el carácter .
Lo más común es que el autómata finito determinista se represente como un gráfico dirigido ("diagrama") tal que: [10]
- El conjunto de vértices del gráfico corresponde al estado de estados ,
- El gráfico tiene un vértice marcado específico correspondiente al estado inicial ,
- El gráfico tiene varios vértices marcados correspondientes al conjunto de estados finales ,
- El conjunto de arcos del gráfico corresponde al conjunto de transiciones ,
- En concreto, cada transición se representa mediante un arco que va desde hasta marcado con el carácter . Esta transición también puede denotarse como .
En términos de su diagrama, el autómata reconoce la palabra sólo si existe un camino desde el vértice inicial hasta algún vértice final tal que la concatenación de caracteres en este camino forme . El conjunto de palabras reconocidas por un autómata forma un lenguaje que está configurado para ser reconocido por el autómata. En estos términos, el lenguaje reconocido por un autómata de sufijo es el lenguaje de sus sufijos (posiblemente vacíos). [9]
Estados del autómata
El "contexto correcto" de la palabra con respecto al lenguaje es un conjunto que es un conjunto de palabras tales que su concatenación con forma una palabra de . Los contextos correctos inducen una relación de equivalencia natural en el conjunto de todas las palabras. Si el lenguaje es reconocido por algún autómata finito determinista, existe un autómata único hasta el isomorfismo que reconoce el mismo lenguaje y tiene el mínimo número posible de estados. Tal autómata se llama autómata mínimo para el lenguaje dado . El teorema de Myhill-Nerode permite definirlo explícitamente en términos de contextos correctos: [11] [12]
El teorema del autómata mínimo que reconoce el lenguaje sobre el alfabeto puede definirse explícitamente de la siguiente manera:
- El alfabeto sigue siendo el mismo,
- Los estados corresponden a los contextos correctos de todas las palabras posibles .
- El estado inicial corresponde al contexto correcto de la palabra vacía ,
- Los estados finales corresponden a los contextos correctos de las palabras de ,
- Las transiciones se dan por , donde y .
En estos términos, un "autómata de sufijos" es el autómata finito determinista mínimo que reconoce el lenguaje de los sufijos de la palabra . El contexto correcto de la palabra con respecto a este lenguaje está formado por palabras , tales que es un sufijo de . Esto permite formular el siguiente lema que define una biyección entre el contexto correcto de la palabra y el conjunto de posiciones correctas de sus ocurrencias en : [13] [14]
Teorema — Sea el conjunto de posiciones correctas de ocurrencias de en .
Existe la siguiente biyección entre y :
- Si , entonces ;
- Si , entonces .
Por ejemplo, para la palabra y su subpalabra , se cumple y . De manera informal, se forma con palabras que siguen a las ocurrencias de hasta el final de y se forma con las posiciones correctas de esas ocurrencias. En este ejemplo, el elemento se corresponde con la palabra mientras que la palabra se corresponde con el elemento .
Esto implica varias propiedades estructurales de los estados del autómata sufijo. Sea , entonces: [14]
- Si y tienen al menos un elemento común , entonces y también tienen un elemento común. Esto implica que es un sufijo de y por lo tanto y . En el ejemplo mencionado anteriormente, , entonces es un sufijo de y por lo tanto y ;
- Si , entonces , por lo tanto, aparece en sólo como sufijo de . Por ejemplo, para y se cumple que y ;
- Si y es un sufijo de tal que , entonces . En el ejemplo anterior y se cumple para el sufijo "intermedio" que .
Cualquier estado del autómata de sufijos reconoce una cadena continua de sufijos anidados de la palabra más larga reconocida por este estado. [14]
La "extensión izquierda" de la cadena es la cadena más larga que tiene el mismo contexto derecho que . La longitud de la cadena más larga reconocida por se denota por . Se cumple: [15]
Teorema — La extensión izquierda de puede representarse como , donde es la palabra más larga tal que cualquier aparición de en está precedida por .
El "enlace de sufijo" del estado es el puntero al estado que contiene el sufijo más grande que no es reconocido por .
En estos términos se puede decir que reconoce exactamente todos los sufijos de que son más largos que y no más largos que . También se cumple: [15]
Teorema — Los enlaces de sufijos forman un árbol que puede definirse explícitamente de la siguiente manera:
- Los vértices del árbol corresponden a las extensiones izquierdas de todas las subcadenas,
- Los bordes del árbol conectan pares de vértices , tales que y .
Conexión con árboles de sufijos

Un " árbol de prefijos " (o "trie") es un árbol dirigido con raíz en el que los arcos están marcados por caracteres de tal manera que ningún vértice de dicho árbol tiene dos arcos salientes marcados con el mismo carácter. Algunos vértices en trie están marcados como finales. Se dice que Trie reconoce un conjunto de palabras definidas por caminos desde su raíz hasta los vértices finales. De esta manera, los árboles de prefijos son un tipo especial de autómatas finitos deterministas si percibe su raíz como un vértice inicial. [16] El "trie de sufijos" de la palabra es un árbol de prefijos que reconoce un conjunto de sus sufijos. "Un árbol de sufijos " es un árbol obtenido a partir de un trie de sufijos mediante el procedimiento de compactación, durante el cual se fusionan los bordes consecuentes si el grado del vértice entre ellos es igual a dos. [15]
Por definición, un autómata de sufijo puede obtenerse mediante la minimización del trie de sufijo. Puede demostrarse que un autómata de sufijo compactado se obtiene mediante la minimización del árbol de sufijo (si se supone que cada cadena en el borde del árbol de sufijo es un carácter sólido del alfabeto) y la compactación del autómata de sufijo. [17] Además de esta conexión entre el árbol de sufijo y el autómata de sufijo de la misma cadena, también existe una conexión entre el autómata de sufijo de la cadena y el árbol de sufijo de la cadena invertida . [18]
De manera similar a los contextos derechos, se pueden introducir "contextos izquierdos" , "extensiones derechas" correspondientes a la cadena más larga que tenga el mismo contexto izquierdo que y la relación de equivalencia . Si se consideran las extensiones derechas con respecto al lenguaje de los "prefijos" de la cadena, se puede obtener: [15]
Teorema — El árbol de sufijos de la cadena puede definirse explícitamente de la siguiente manera:
- Los vértices del árbol corresponden a extensiones derechas de todas las subcadenas,
- Las aristas corresponden a tripletes tales que y .
Aquí triplete significa que hay un borde de a con la cuerda escrita en él
, lo que implica que el árbol de enlace de sufijos de la cadena y el árbol de sufijos de la cadena son isomorfos: [18]
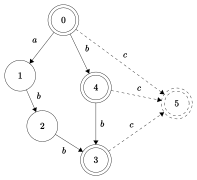
| Estructuras de sufijos de las palabras "abbcbc" y "cbcbba" |
|---|
|
De manera similar al caso de las extensiones izquierdas, el siguiente lema se aplica a las extensiones derechas: [15]
Teorema : La extensión derecha de la cadena se puede representar como , donde es la palabra más larga tal que cada aparición de en es sucedida por .
Tamaño
Un autómata sufijo de la cadena de longitud tiene como máximo estados y como máximo transiciones. Estos límites se alcanzan en las cadenas y correspondientemente. [13] Esto se puede formular de una manera más estricta como donde y son los números de transiciones y estados en el autómata correspondientemente. [14]
| Autómatas de sufijo máximo |
|---|
|
Construcción
Inicialmente el autómata sólo consta de un único estado correspondiente a la palabra vacía, luego se van añadiendo los caracteres de la cadena uno a uno y el autómata se reconstruye en cada paso de forma incremental. [19]
Actualizaciones estatales
Después de que se añade un nuevo carácter a la cadena, se modifican algunas clases de equivalencia. Sea el contexto correcto de con respecto al lenguaje de los sufijos. Entonces, la transición de a después de que se añade a se define mediante el lema: [14]
Teorema : Sean algunas palabras y algún carácter de este alfabeto. Entonces existe la siguiente correspondencia entre y :
- si es un sufijo de ;
- de lo contrario.
Después de añadir a la palabra actual el contexto correcto de puede cambiar significativamente solo si es un sufijo de . Esto implica que la relación de equivalencia es un refinamiento de . En otras palabras, si , entonces . Después de la adición de un nuevo carácter , se dividirán como máximo dos clases de equivalencia de y cada una de ellas puede dividirse como máximo en dos nuevas clases. Primero, la clase de equivalencia correspondiente al contexto correcto vacío siempre se divide en dos clases de equivalencia, una de ellas correspondiente a sí misma y que tiene como contexto correcto. Esta nueva clase de equivalencia contiene exactamente y todos sus sufijos que no ocurrieron en , ya que el contexto correcto de tales palabras estaba vacío antes y ahora solo contiene palabras vacías. [14]
Dada la correspondencia entre los estados del autómata de sufijos y los vértices del árbol de sufijos, es posible averiguar el segundo estado que puede dividirse después de que se añada un nuevo carácter. La transición de a corresponde a la transición de a en la cadena invertida. En términos de árboles de sufijos, corresponde a la inserción del nuevo sufijo más largo en el árbol de sufijos de . Como máximo, se pueden formar dos nuevos vértices después de esta inserción: uno de ellos correspondiente a , mientras que el otro corresponde a su antecesor directo si hubo una ramificación. Volviendo a los autómatas de sufijos, significa que el primer nuevo estado reconoce y el segundo (si hay un segundo nuevo estado) es su enlace de sufijo. Puede enunciarse como un lema: [14]
Teorema : Sea , alguna palabra y carácter sobre . Sea también el sufijo más largo de , que aparece en , y sea . Entonces, para cualquier subcadena de , se cumple:
- Si y , entonces ;
- Si y , entonces ;
- Si y , entonces .
Esto implica que si (por ejemplo, cuando no ocurrió en absoluto y ), entonces solo se divide la clase de equivalencia correspondiente al contexto derecho vacío. [14]
Además de los enlaces de sufijos, también es necesario definir estados finales del autómata. De las propiedades de estructura se deduce que todos los sufijos de una palabra reconocidos por son reconocidos por algún vértice en la ruta de sufijos de . Es decir, los sufijos con una longitud mayor que se encuentran en , los sufijos con una longitud mayor que pero no mayor que se encuentran en , y así sucesivamente. Por lo tanto, si el estado que reconoce se denota por , entonces todos los estados finales (es decir, los sufijos que reconocen de ) forman la secuencia . [19]
Actualizaciones de transiciones y enlaces de sufijos
Después de que el carácter se añade a los posibles nuevos estados del autómata de sufijo son y . El enlace de sufijo de va a y de va a . Las palabras de aparecen en solo como sus sufijos, por lo tanto, no debería haber transiciones en absoluto desde mientras que las transiciones a deben ir desde sufijos de que tengan una longitud de al menos y estar marcadas con el carácter . El estado está formado por un subconjunto de , por lo tanto, las transiciones de deben ser las mismas que las de . Mientras tanto, las transiciones que conducen a deben ir desde sufijos de que tengan una longitud menor que y al menos , ya que dichas transiciones han conducido a antes y correspondieron a una parte separada de este estado. Los estados correspondientes a estos sufijos se pueden determinar mediante el recorrido de la ruta de enlace de sufijo para . [19]
Algoritmo de construcción
Los resultados teóricos anteriores conducen al siguiente algoritmo que toma el carácter y reconstruye el autómata de sufijo de en el autómata de sufijo de : [19]
- El estado correspondiente a la palabra se mantiene como ;
- Después de agregarlo, el valor anterior de se almacena en la variable y se reasigna al nuevo estado correspondiente a ;
- Los estados correspondientes a los sufijos de se actualizan con transiciones a . Para ello se debe recorrer , hasta que exista un estado que ya tenga una transición de ;
- Una vez finalizado el bucle mencionado anteriormente, se dan 3 casos:
- Si ninguno de los estados en la ruta del sufijo tuvo una transición por , entonces nunca ocurrió en antes y el enlace del sufijo de debe conducir a ;
- Si se encuentra la transición por y conduce del estado al estado , tal que , entonces no tiene que dividirse y es un enlace de sufijo de ;
- Si se encuentra la transición pero , entonces las palabras que tienen una longitud máxima deben segregarse en un nuevo estado "clon" ;
- Si el paso anterior concluyó con la creación de , las transiciones de éste y su sufijo enlace deben copiar las de , al mismo tiempo se asigna como enlace de sufijo común de ambos y ;
- Las transiciones que han llevado a antes pero que corresponden a palabras de longitud máxima se redirigen a . Para ello, se continúa recorriendo la ruta del sufijo de hasta que se encuentre el estado tal que la transición de desde no lleve a .
Todo el procedimiento se describe mediante el siguiente pseudocódigo: [19]
función add_letter(x) : define p = last asigna last = new_state() asigna len(last) = len(p) + 1 mientras δ(p, x) no está definido: asigna δ(p, x) = last, p = link(p) define q = δ(p, x) si q = last : asigna link(last) = q 0 de lo contrario si len(q) = len(p) + 1 : asigna link(last) = q de lo contrario : define cl = new_state() asigna len(cl) = len(p) + 1 asigna δ(cl) = δ(q), link(cl) = link(q) asigna link(last) = link(q) = cl mientras δ(p, x) = q : asigna δ(p, x) = cl, p = link(p)
Aquí se encuentra el estado inicial del autómata y es una función que crea un nuevo estado para él. Se supone que , , y se almacenan como variables globales. [19]
Complejidad
La complejidad del algoritmo puede variar dependiendo de la estructura subyacente utilizada para almacenar las transiciones del autómata. Puede implementarse en con sobrecarga de memoria o en con sobrecarga de memoria si se supone que la asignación de memoria se realiza en . Para obtener dicha complejidad, uno tiene que utilizar los métodos de análisis amortizado . El valor de se reduce estrictamente con cada iteración del ciclo, mientras que solo puede aumentar hasta en uno después de la primera iteración del ciclo en la siguiente llamada add_letter . El valor general de nunca excede y solo aumenta en uno entre iteraciones de adición de nuevas letras que sugieren que la complejidad total también es lineal como máximo. La linealidad del segundo ciclo se muestra de manera similar. [19]
Generalizaciones
El autómata de sufijo está estrechamente relacionado con otras estructuras de sufijo e índices de subcadenas . Dado un autómata de sufijo de una cadena específica, se puede construir su árbol de sufijos mediante compactación y recorrido recursivo en tiempo lineal. [20] Se pueden realizar transformaciones similares en ambas direcciones para cambiar entre el autómata de sufijo de y el árbol de sufijo de cadena invertida . [18] Además de esto, se desarrollaron varias generalizaciones para construir un autómata para el conjunto de cadenas dado por trie, [8] automatización de sufijo compactada (CDAWG), [7] para mantener la estructura del autómata en la ventana deslizante, [21] y para construirlo de manera bidireccional, admitiendo la inserción de caracteres tanto al principio como al final de la cadena. [22]
Autómata de sufijo compactado
Como ya se mencionó anteriormente, un autómata de sufijo compactado se obtiene mediante la compactación de un autómata de sufijo regular (eliminando estados que no son finales y tienen exactamente un arco saliente) y la minimización de un árbol de sufijos. De manera similar al autómata de sufijo regular, los estados del autómata de sufijo compactado se pueden definir de manera explícita. Una extensión bidireccional de una palabra es la palabra más larga , de modo que cada ocurrencia de en es precedida y sucedida por . En términos de extensiones izquierda y derecha significa que la extensión bidireccional es la extensión izquierda de la extensión derecha o, lo que es equivalente, la extensión derecha de la extensión izquierda, es decir . En términos de extensiones bidireccionales, el autómata compactado se define de la siguiente manera: [15]
Teorema — El autómata sufijo compactado de la palabra se define mediante un par , donde:
- es un conjunto de estados de autómata;
- es un conjunto de transiciones de autómatas.
Las extensiones bidireccionales inducen una relación de equivalencia que define el conjunto de palabras reconocidas por el mismo estado del autómata compactado. Esta relación de equivalencia es un cierre transitivo de la relación definida por , que resalta el hecho de que un autómata compactado puede obtenerse tanto pegando vértices de árboles de sufijos equivalentes mediante una relación (minimización del árbol de sufijos) como pegando estados de autómatas de sufijos equivalentes mediante una relación (compactación del autómata de sufijo). [23] Si las palabras y tienen las mismas extensiones derechas, y las palabras y tienen las mismas extensiones izquierdas, entonces, acumulativamente, todas las cadenas , y tienen las mismas extensiones bidireccionales. Al mismo tiempo, puede suceder que ni las extensiones izquierda ni derecha de y coincidan. Como ejemplo, se puede tomar , y , para las cuales las extensiones izquierda y derecha son las siguientes: , pero y . Dicho esto, mientras que las relaciones de equivalencia de extensiones unidireccionales se formaron mediante alguna cadena continua de prefijos o sufijos anidados, las relaciones de equivalencia de extensiones bidireccionales son más complejas y lo único que se puede concluir con seguridad es que las cadenas con la misma extensión bidireccional son subcadenas de la cadena más larga que tiene la misma extensión bidireccional, pero incluso puede suceder que no tengan ninguna subcadena no vacía en común. El número total de clases de equivalencia para esta relación no excede lo que implica que el autómata de sufijo compactado de la cadena que tiene longitud tiene como máximo estados. La cantidad de transiciones en dicho autómata es como máximo . [15]
Autómata sufijo de varias cadenas
Consideremos un conjunto de palabras . Es posible construir una generalización de un autómata de sufijos que reconocería el lenguaje formado por los sufijos de todas las palabras del conjunto. Las restricciones para el número de estados y transiciones en dicho autómata permanecerían iguales que para un autómata de una sola palabra si ponemos . [23] El algoritmo es similar a la construcción de un autómata de una sola palabra excepto que en lugar del estado, la función add_letter trabajaría con el estado correspondiente a la palabra asumiendo la transición del conjunto de palabras al conjunto . [24] [25]
Esta idea se generaliza aún más al caso en el que no se da explícitamente sino que se da mediante un árbol de prefijos con vértices. Mohri et al . demostraron que un autómata de este tipo tendría como máximo y puede construirse en tiempo lineal a partir de su tamaño. Al mismo tiempo, el número de transiciones en dicho autómata puede alcanzar , por ejemplo, para el conjunto de palabras sobre el alfabeto, la longitud total de las palabras es igual a , el número de vértices en el trie de sufijo correspondiente es igual a y el autómata de sufijo correspondiente está formado por estados y transiciones. El algoritmo sugerido por Mohri repite principalmente el algoritmo genérico para construir un autómata de varias cadenas, pero en lugar de hacer crecer las palabras una por una, recorre el trie en un orden de búsqueda en amplitud y agrega nuevos caracteres a medida que los encuentra en el recorrido, lo que garantiza una complejidad lineal amortizada. [26]
Ventana corrediza
Algunos algoritmos de compresión , como LZ77 y RLE, pueden beneficiarse de almacenar un autómata de sufijo o una estructura similar no para toda la cadena sino solo para los últimos caracteres mientras se actualiza la cadena. Esto se debe a que la compresión de datos suele ser expresivamente grande y el uso de memoria no es deseable. En 1985, Janet Blumer desarrolló un algoritmo para mantener un autómata de sufijo en una ventana deslizante de tamaño en el peor de los casos y en promedio, asumiendo que los caracteres se distribuyen de forma independiente y uniforme . También demostró que la complejidad no se puede mejorar: si se consideran palabras construidas como una concatenación de varias palabras, donde , entonces el número de estados para la ventana de tamaño cambiaría con frecuencia con saltos de orden , lo que hace imposible incluso la mejora teórica de para autómatas de sufijo regulares. [27]
Lo mismo debería ser cierto para el árbol de sufijos porque sus vértices corresponden a estados del autómata de sufijos de la cadena invertida, pero este problema puede resolverse al no almacenar explícitamente cada vértice correspondiente al sufijo de toda la cadena, almacenando así solo los vértices con al menos dos aristas salientes. En 1989, Edward Fiala y Daniel Greene sugirieron una variación del algoritmo de construcción de árboles de sufijos de McCreight para esta tarea; [28] varios años después, Jesper Larsson obtuvo un resultado similar con la variación del algoritmo de Ukkonen . [29] [30] La existencia de un algoritmo de este tipo, para un autómata de sufijos compactado que absorba algunas propiedades tanto de los árboles de sufijos como de los autómatas de sufijos, fue una cuestión abierta durante mucho tiempo hasta que Martin Senft y Tomasz Dvorak descubrieron en 2008 que es imposible si el tamaño del alfabeto es al menos dos. [31]
Una forma de superar este obstáculo es permitir que el ancho de la ventana varíe un poco mientras se mantiene . Esto se puede lograr mediante un algoritmo aproximado sugerido por Inenaga et al. en 2004. No se garantiza que la ventana para la que se construye el autómata de sufijo en este algoritmo tenga una longitud, pero se garantiza que tenga al menos y como máximo, al tiempo que se proporciona una complejidad general lineal del algoritmo. [32]
Aplicaciones
El autómata sufijo de la cadena se puede utilizar para resolver problemas como: [33] [34]
- Contando el número de subcadenas distintas de en línea,
- Encontrar la subcadena más larga de que aparece al menos dos veces en ,
- Encontrar la subcadena común más larga de y en ,
- Contando el número de ocurrencias de en en ,
- Encontrar todas las ocurrencias de en , donde es el número de ocurrencias.
Se supone aquí que se da en la entrada después de que se construye el sufijo del autómata. [33]
Los autómatas de sufijo también se utilizan en la compresión de datos, [35] la recuperación de música [36] [37] y la coincidencia de secuencias del genoma. [38]
Referencias
- ^ ab Crochemore y Vérin (1997), pág. 192
- ^ de Weiner (1973)
- ^ Pratt (1973)
- ^ Slisenko (1983)
- ^ Blumer y otros (1984), pág. 109
- ^ Chen y Seiferas (1985), pág. 97
- ^ ab Blumer y otros (1987), pág. 578
- ^ ab Inenaga et al. (2001), pág. 1
- ^ ab Crochemore y Hancart (1997), págs. 3-6
- ^ ab Serebryakov et al. (2006), págs. 50–54
- ^ Рубцов (2019), págs. 89–94
- ^ Hopcroft y Ullman (1979), págs. 65-68
- ^ ab Blumer y otros (1984), págs. 111-114
- ^ abcdefgh Crochemore y Hancart (1997), págs. 27-31
- ^ abcdefg Inenaga et al. (2005), págs. 159-162
- ^ Rubinchik y Shur (2018), págs. 1-2
- ^ Inénaga et al. (2005), págs. 156-158
- ^ abc Fujishige y col. (2016), págs. 1-3
- ^ abcdefg Crochemore y Hancart (1997), págs. 31-36
- ^ Паращенко (2007), págs. 19-22
- ^ Blumer (1987), pág. 451
- ^ Inenaga (2003), pág. 1
- ^ ab Blumer y otros (1987), págs. 585-588
- ^ Blumer y otros (1987), págs. 588-589
- ^ Blumer y otros (1987), pág. 593
- ^ Mohri, Moreno y Weinstein (2009), págs. 3558–3560
- ^ Blumer (1987), págs. 461–465
- ^ Fiala y Greene (1989), pág. 490
- ^ Larsson (1996)
- ^ Brodnik y Jekovec (2018), pág. 1
- ^ Senft y Dvořák (2008), pág. 109
- ^ Inenaga y otros (2004)
- ^ ab Crochemore y Hancart (1997), págs. 36-39
- ^ Crochemore y Hancart (1997), págs. 39-41
- ^ Yamamoto y col. (2014), pág. 675
- ^ Crochemore y col. (2003), pág. 211
- ^ Mohri, Moreno y Weinstein (2009), pág. 3553
- ^ Faro (2016), pág. 145
Bibliografía
- Blumer, A.; Blumer, J.; Ehrenfeucht, A.; Haussler, D.; McConnell, R. (1984). "Construcción del DFA mínimo para el conjunto de todas las subpalabras de una palabra en línea en tiempo lineal". Autómatas, lenguajes y programación . Apuntes de clase en informática. Vol. 172. págs. 109–118. doi :10.1007/3-540-13345-3_9. ISBN 978-3-540-13345-2.
- Blumer, A.; Blumer, J.; Haussler, D.; McConnell, R.; Ehrenfeucht, A. (1987). "Archivos invertidos completos para una recuperación y análisis de texto eficiente". Revista de la ACM . 34 (3): 578–595. doi :10.1145/28869.28873. Zbl 1433.68118.
- Blumer, Janet A. (1987). "¿Cuánto es ese DAWG en la ventana? Un algoritmo de ventana móvil para el gráfico de palabras acíclico dirigido". Journal of Algorithms . 8 (4): 451–469. doi :10.1016/0196-6774(87)90045-9. Zbl 0636.68109.
- Brodnik, Andrej; Jekovec, Matevž (2018). "Árbol de sufijos deslizantes". Algoritmos . 11 (8): 118. doi : 10.3390/A11080118 . Zbl 1458.68043.
- Chen, MT; Seiferas, Joel (1985). "Construcción eficiente y elegante de árboles de subpalabras". Algoritmos combinatorios en palabras . págs. 97–107. doi :10.1007/978-3-642-82456-2_7. ISBN 978-3-642-82458-6.
- Crochemore, Maxime; Hancart, Christophe (1997). "Autómatas para emparejar patrones". Manual de lenguajes formales . págs. 399–462. doi :10.1007/978-3-662-07675-0_9. ISBN 978-3-642-08230-6.
- Crochemore, Maxime; Vérin, Renaud (1997). "Sobre grafos de palabras acíclicos dirigidos y compactos". Estructuras en lógica y ciencias de la computación . Apuntes de clase en ciencias de la computación. Vol. 1261. págs. 192–211. doi :10.1007/3-540-63246-8_12. ISBN 978-3-540-63246-7.
- Crochemore, Maxime; Iliopoulos, Costas S.; Navarro, Gonzalo; Pinzón, Yoan J. (2003). "Un enfoque de autómata de sufijo paralelo de bits para la coincidencia (δ, γ) en la recuperación de música". Procesamiento de cadenas y recuperación de información . Apuntes de conferencias sobre informática. vol. 2857, págs. 211–223. doi :10.1007/978-3-540-39984-1_16. ISBN 978-3-540-20177-9.
- Serebryakov, Vladimir; Galochkin, Maksim Pavlovich; Furugian, Meran Gabibullaevich; Gonchar, Dmitriy Ruslanovich (2006). Теория и реализация языков программирования: Учебное пособие (PDF) (en ruso). Moscú: MZ Press. ISBN 5-94073-094-9.
- Faro, Simone (2016). "Evaluación y mejora de algoritmos rápidos para la correspondencia exacta de secuencias genómicas". Algorithms for Computational Biology . Lecture Notes in Computer Science. Vol. 9702. págs. 145–157. doi :10.1007/978-3-319-38827-4_12. ISBN 978-3-319-38826-7.
- Fiala, ER; Greene, DH (1989). "Compresión de datos con ventanas finitas". Comunicaciones de la ACM . 32 (4): 490–505. doi :10.1145/63334.63341.
- Fujishige, Yuta; Tsujimaru, Yuki; Inenaga, Shunsuke; Bannai, Hideo; Takeda, Masayuki (2016). "Computación de DAWG y palabras ausentes mínimas en tiempo lineal para alfabetos enteros". 41.° Simposio internacional sobre fundamentos matemáticos de la informática (MFCS 2016) . Leibniz International Proceedings in Informatics. Schloss Dagstuhl – Leibniz-Zentrum für Informatik. doi : 10.4230/LIPICS.MFCS.2016.38 . Zbl 1398.68703.
- Hopcroft, John Edward; Ullman, Jeffrey David (1979). Introducción a la teoría de autómatas, lenguajes y computación (1.ª ed.). Massachusetts: Addison-Wesley. ISBN 978-81-7808-347-6. Número OL 9082218M.
- Inenaga, Shunsuke (2003). "Construcción bidireccional de árboles de sufijos" (PDF) . Nordic Journal of Computing . 10 (1): 52–67. CiteSeerX 10.1.1.100.8726 .
- Inenaga, Shunsuke; Hoshino, Hiromasa; Shinohara, Ayumi; Takeda, Masayuki; Arikawa, Setsuo; Mauri, Giancarlo; Pavesi, Giulio (2005). "Construcción en línea de gráficos de palabras acíclicos dirigidos compactos". Matemática Aplicada Discreta . 146 (2): 156-179. doi :10.1016/J.DAM.2004.04.012. Zbl 1084.68137.
- Inenaga, Shunsuke; Hoshino, Hiromasa; Shinohara, Ayumi; Takeda, Masayuki; Arikawa, Setsuo (2001). «Construcción del CDAWG por un tiempo» (PDF) . Conferencia de Stringología de Praga. Procedimientos . págs. 37–48. CiteSeerX 10.1.1.24.2637 .
- Inenaga, Shunsuke; Shinohara, Ayumi; Takeda, Masayuki; Arikawa, Setsuo (2004). "Gráficos de palabras acíclicos dirigidos compactos para una ventana deslizante". Revista de algoritmos discretos . 2 : 33–51. doi :10.1016/S1570-8667(03)00064-9. Zbl 1118.68755.
- Larsson, NJ (1996). "Aplicación extendida de árboles de sufijos a la compresión de datos". Actas de la Conferencia sobre compresión de datos - DCC '96 . págs. 190-199. doi :10.1109/DCC.1996.488324. ISBN 0-8186-7358-3.
- Mohri, Mehryar; Moreno, Pedro; Weinstein, Eugene (2009). "Algoritmo general de construcción de autómatas de sufijo y límites espaciales". Ciencias de la Computación Teórica . 410 (37): 3553–3562. doi :10.1016/J.TCS.2009.03.034. Zbl 1194.68143.
- Паращенко, Дмитрий А. (2007). Обработка строк на основе суффиксных автоматов (PDF) (en ruso). San Petersburgo: Universidad ITMO.
- Pratt, Vaughan Ronald (1973). Mejoras y aplicaciones para el buscador de repeticiones de Weiner . OCLC 726598262.
- Рубцов, Александр Александрович (2019). Заметки и задачи о регулярных языках и конечных автоматах (PDF) (en ruso). Moscú: Instituto de Física y Tecnología de Moscú. ISBN 978-5-7417-0702-9.
- Rubichik, Mijaíl; Shur, Arseny M. (2018). "EERTREE: una estructura de datos eficiente para procesar palíndromos en cadenas". Revista europea de combinatoria . 68 : 249–265. arXiv : 1506.04862 . doi :10.1016/J.EJC.2017.07.021. Zbl 1374.68131.
- Senft, Martin; Dvořák, Tomáš (2008). "Perfección deslizante de CDAWG". Procesamiento de cadenas y recuperación de información . Apuntes de clase en informática. Vol. 5280. págs. 109–120. doi :10.1007/978-3-540-89097-3_12. ISBN 978-3-540-89096-6.
- Slisenko, AO (1983). "Detección de periodicidades y emparejamiento de cadenas en tiempo real". Revista de matemáticas soviéticas . 22 (3): 1316–1387. doi :10.1007/BF01084395. Zbl 0509.68043.
- Weiner, Peter (1973). "Algoritmos de coincidencia de patrones lineales". 14.º Simposio anual sobre conmutación y teoría de autómatas (SWAT 1973) . págs. 1–11. doi :10.1109/SWAT.1973.13.
- Yamamoto, Jun'ichi; I, Tomohiro; Bannai, Hideo; Inenaga, Shunsuke; Takeda, Masayuki (2014). "Factorización Lempel-Ziv en línea compacta y más rápida". 31.° Simposio internacional sobre aspectos teóricos de la informática (STACS 2014) . Leibniz International Proceedings in Informatics. Schloss Dagstuhl – Leibniz-Zentrum für Informatik. doi : 10.4230/LIPICS.STACS.2014.675 . Zbl 1359.68341.





















































![{\textstyle q_{1}{\begin{smallmatrix}{\sigma }\\[-5pt]{\longrightarrow }\end{smallmatrix}}q_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16652b5477735b6587a69159e7dc29f9e349fe10)



![{\displaystyle [\omega ]_{R}=\{\alpha :\omega \alpha \en L\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e11883b4ac05c6aecf539854d6b75c9ef741f92)
![{\displaystyle [\alpha ]_{R}=[\beta ]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a98b44d0cd19b729ad56a393d0eaec1805c8e39b)
![{\displaystyle [\omega ]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d0d285bcdf8a938d706449db49bf9412fa4d28c)
![{\displaystyle [\varepsilon ]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0760f6b8f45135b6a59cd46f3e0fbaf6fe048e87)

![{\displaystyle [\omega ]_{R}{\begin{smallmatrix}{\sigma }\\[-5pt]{\longrightarrow }\end{smallmatrix}}[\omega \sigma ]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/608b0d4e9d7dc30de4e7a50378e05b04f2c5a829)




![{\displaystyle s_{x+1}s_{x+2}\puntos s_{n}\en [\omega ]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7236e1094224b68350522b3c78e3b25c7d7590c7)
![{\displaystyle \alpha \en [\omega ]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43d734319905e4142a99b88b1a4ff78848e2db43)




![{\displaystyle [ab]_{R}=\{a,acaba\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f08d2df6474465c79e95062c1fb852ab40b5f9a)
![estilo de visualización {\displaystyle [ab]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ed7efb19a8c1c679df529cc521396f5084dc6bc)



![{\displaystyle s_{3}s_{4}s_{5}s_{6}s_{7}=acaba\in [ab]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c276d63dd14d389a3bc61bd2ac4ec6dd79440d1c)
![{\displaystyle a\in[ab]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95e7352493337857728aadbf551c04e533d5e6db)


![{\displaystyle [\alpha ]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71085cf6f872adc3d86197ac113b94084f5345c9)
![{\displaystyle [\beta ]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b458c8d348b152c8ce7c446dba72e2a9c06c739)




![{\displaystyle [\beta ]_{R}\subconjunto [\alpha ]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/120910cc963d194c5a2e72aaabeccd99762bb0cb)
![{\displaystyle a\in[ab]_{R}\cap[cab]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/290e157059e4c8570e934f79b954cbc33dad920d)

![{\displaystyle [cab]_{R}=\{a\}\subconjunto \{a,acaba\}=[ab]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e09d83b6c56e7c9e8dfd2d011bf221f0fb43937d)




![{\displaystyle [b]_{R}=[ab]_{R}=\{a,acaba\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b44e32ec0f0fc2800c6a07868a498acf9e7200b)


![{\displaystyle [\alpha ]_{R}=[\gamma ]_{R}=[\beta ]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ff07aea00a27624cd9ee051aed79421a3e707c8)
![{\displaystyle [c]_{R}=[bac]_{R}=\{aba\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3211d738bcd0308264c98a087e9538bb5c9fbc76)

![{\displaystyle [ac]_{R}=\{aba\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7121eb2486dab490f0f2f0fce9c4738d130c4979)
![{\displaystyle q=[\alpha ]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b41dd70277955f02fec50f8fb0f15aac98944de2)


![{\displaystyle q=[\gamma ]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa3035b4f3dae96f18646d8eb7ffad7443c84355)















![{\displaystyle [\omega ]_{L}=\{\beta \en \Sigma ^{*}:\beta \omega \en L\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e52cedfd75f0212d1e994dd4e26244482923cff)

![{\displaystyle [\alpha ]_{L}=[\beta ]_{L}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0476adeb02a48c9623b9a037d45d9e7cc104594)
























![{\displaystyle [\alpha ]_{R_{\omega }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf5092b4d6aa56f342180faa815e616310a766a1)
![{\displaystyle [\alpha ]_{R_{\omega x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bc63f277d664c127ea435f4ec937f065812790c)

![{\displaystyle [\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x\cup \{\varepsilon \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62af9ba620fb1df6646ec322efe363af38d33047)

![{\displaystyle [\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aea54945b739d0e96a6ed3769826a24a6bca469b)


![{\displaystyle [\alpha ]_{R_{\omega x}}=[\beta ]_{R_{\omega x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8720b747c926636d4f25ae02fd22c02e6cee6f2a)
![{\displaystyle [\alpha ]_{R_{\omega }}=[\beta ]_{R_{\omega }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35041a5b568ed31c1c4bafcf28d5dc300a2bdd4d)





![{\displaystyle [u]_{R_{\omega }}=[v]_{R_{\omega }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/432b8eb68fefcd343856cd77b50e1a6da1bf7226)
![{\displaystyle [u]_{R_{\omega }}\neq [\alpha ]_{R_{\omega }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4c5d2ddc8543be4dee9f0dd9607f27ca70d1b93)
![{\displaystyle [u]_{R_{\omega x}}=[v]_{R_{\omega x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d507f1de166b155876cfde9762eaa827a4d147fe)
![{\displaystyle [u]_{R_{\omega }}=[\alpha ]_{R_{\omega }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d49bd348b535edf97e44b2ee3ff525eb717a44f)

![{\displaystyle [u]_{R_{\omega x}}=[\alpha ]_{R_{\omega x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc2ae2510aa9e9ee2d0f6ec623fdb4bf70ffacdd)

![{\displaystyle [u]_{R_{\omega x}}=[\beta ]_{R_{\omega x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e6d5e324fa555ebe1942df7367ebadc6c1f9353)






![{\displaystyle [\omega x]_{R_{\omega x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fc3ec8722532016ceae828eeaf081202ac42b05)
![{\displaystyle enlace([\alpha ]_{R_{\omega }})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91d45b00112aebf52e311e9255240351d52531c2)

![{\displaystyle len(link([\alpha ]_{R_{\omega }}))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ddac98ddeaf4716b89cf8092632952e5ae753e5)
![{\displaystyle [\omega ]_{R_{\omega }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3af043acf29d9539fa3e1c72adfb971594474df)