Diagrama de Snellen

Diagrama de Snellen
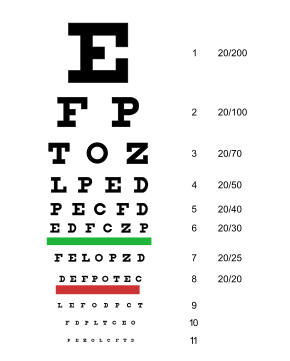Objetivo	La tabla de Snellen se utiliza para estimar la agudeza visual (las últimas tres filas son 20/15, 20/13 y 20/10)

Una tabla de Snellen es una tabla optométrica que se puede utilizar para medir la agudeza visual . Las tablas de Snellen reciben su nombre del oftalmólogo holandés Herman Snellen , quien desarrolló la tabla en 1862 como una herramienta de medición para la fórmula de agudeza desarrollada por su profesor Franciscus Cornelius Donders . ^{[1] [2]} Muchos oftalmólogos y científicos de la visión ahora utilizan una tabla mejorada conocida como tabla LogMAR .

Snellen desarrolló gráficos utilizando símbolos basados ​​en una cuadrícula de unidades de 5×5. Los gráficos experimentales desarrollados en 1861 utilizaban símbolos abstractos. ^[3] Los gráficos de Snellen publicados en 1862 utilizaban mayúsculas alfanuméricas en la cuadrícula de 5×5. El gráfico original muestra A, C, E, G, L, N, P, R, T, 5, V, Z, B, D, 4, F, H, K, O, S, 3, U, Y, A, C, E, G, L, 2. ^[2]

La tabla de Snellen normal está impresa con once líneas de letras mayúsculas. La primera línea consta de una letra muy grande, que puede ser una de varias letras, por ejemplo E, H o N. Las filas siguientes tienen un número creciente de letras que disminuyen de tamaño. Una persona que realiza la prueba se cubre un ojo a 6 metros o 20 pies de distancia y lee en voz alta las letras de cada fila, comenzando por la parte superior. La fila más pequeña que se puede leer con precisión indica la agudeza visual en ese ojo específico. Los símbolos en una tabla de agudeza visual se conocen formalmente como " optotipos ".

En el caso de la tabla Snellen tradicional, los optotipos tienen la apariencia de letras de imprenta y están pensados ​​para ser vistos y leídos como letras. Sin embargo, no son letras de una fuente tipográfica cualquiera. Tienen una geometría particular y sencilla en la que:

• El grosor de las líneas es igual al grosor de los espacios en blanco entre líneas y al grosor del espacio en la letra "C"
• La altura y el ancho del optotipo (letra) es cinco veces el grosor de la línea.

En la tabla de Snellen común sólo se utilizan las nueve letras C, D, E, F, L, O, P, T, Z. La percepción de cinco de seis letras (o una proporción similar) se considera la fracción de Snellen. ^[4] Las tablas de Snellen montadas en la pared son económicas y a veces se utilizan para la evaluación aproximada de la visión, por ejemplo, en el consultorio de un médico de atención primaria. Siempre que se debe evaluar la agudeza con cuidado (como en un examen de un oftalmólogo) o cuando existe la posibilidad de que el examinado intente engañar al examinador (como en una oficina de licencias de vehículos de motor), se utiliza un equipo que puede presentar las letras en una variedad de patrones aleatorios. La norma BS 4274-1:1968 (British Standards Institution) "Especificación para tablas de prueba para determinar la agudeza visual a distancia" fue reemplazada por la norma BS 4274-1:2003 "Tablas de prueba para la determinación clínica de la agudeza visual a distancia - Especificación". En él se establece que "la luminancia de la presentación debe ser uniforme y no inferior a 120 cd/m2 ^. Cualquier variación en la tabla de prueba no debe superar el 20 %". Según la norma BS 4274-1:2003, solo se deben utilizar las letras C, D, E, F, H, K, N, P, R, U, V y Z para la prueba de visión en función de la legibilidad uniforme de las letras. ^{[ cita requerida ]}

La agudeza visual es la distancia a la que se realiza la prueba/distancia a la que el optotipo más pequeño identificado subtiende un ángulo de cinco minutos de arco y las características distintivas críticas del optotipo subtienden un ángulo de un minuto de arco. ^{[5] [2]}

Snellen definió la "visión estándar" como la capacidad de reconocer uno de sus optotipos cuando éste abarca 5 minutos de arco. Por lo tanto, el optotipo sólo puede reconocerse si la persona que lo observa puede discriminar un patrón espacial separado por un ángulo visual de un minuto de arco .

Fuera de los Estados Unidos, la distancia estándar de la tabla es de 6 metros (20 pies) y la agudeza visual normal se designa como "6/6". Otras agudezas visuales se expresan como proporciones con un numerador de 6. Algunas clínicas no tienen carriles oculares de 6 metros disponibles, y se utiliza una tabla de tamaño medio que subtiende los mismos ángulos a 3 metros (9,8 pies) o una tabla invertida proyectada y observada en un espejo para lograr las letras del tamaño correcto.

En la prueba de agudeza visual más conocida, se coloca una tabla de Snellen a una distancia estándar: 6 metros. A esta distancia, los símbolos de la línea que representan la agudeza visual "normal" subtienden un ángulo de cinco minutos de arco, y el grosor de las líneas y de los espacios entre ellas subtiende un minuto de arco. Esta línea, designada 6/6 (o 20/20), es la línea más pequeña que una persona con agudeza visual normal puede leer a una distancia de 6 metros. Esta definición es arbitraria, ya que los ojos humanos suelen tener una agudeza visual superior, como escribe Tscherning: "Hemos descubierto también que los mejores ojos tienen una agudeza visual que se acerca a 2, y podemos estar casi seguros de que si, con una buena iluminación, la agudeza visual es sólo igual a 1, el ojo presenta defectos lo suficientemente pronunciados como para ser fácilmente detectados". ^[6]

Tres líneas más arriba, las letras tienen el doble de altura que las letras de la línea 6/6 (o 20/20 en los EE. UU.). Si esta es la línea más pequeña que una persona puede leer, su agudeza visual es "6/12" ("20/40"), lo que significa que esta persona necesita acercarse a una distancia de 6 metros (20 pies) para leer letras que una persona con agudeza visual normal podría leer a 12 metros (39 pies). De una manera aún más aproximada, se podría decir que esta persona tiene "la mitad" de la agudeza visual normal de 6/6.

A una distancia exacta de 6 metros del paciente, las letras de la línea 6/6 deben subtender 5 minutos de arco (de modo que los extremos individuales de las letras subtienden 1 minuto de arco), lo que significa que el diagrama debe tener un tamaño tal que estas letras tengan una altura de 8,73 mm y la "E" superior (6/60) debe tener una altura de 87,3 mm. Dicho de otro modo, el ojo debe estar a una distancia de 68,76 veces la altura de la letra superior (6/60). La fórmula es

$${\displaystyle w=2d\,{\tan {{\theta } \sobre {2}}}}$$

donde es la altura o el ancho del optotipo (que son los mismos debido a que el optotipo está en una cuadrícula), es la distancia del ojo a la tabla, y es el ángulo subtendido por el optotipo, que es de 5 minutos de arco según lo especificado por Snellen. ^[7] Otro cálculo para clínicas de los Estados Unidos que utiliza distancias de tabla de 20 pies (un poco más de 6 m), y utiliza un ojo modelo de 17 mm para los cálculos, y una letra que subtiende 5 minutos de arco, da una altura vertical de la letra 20/20 de 8,75 mm. ^[8]${\estilo de visualización w}$${\estilo de visualización d}$${\estilo de visualización \theta}$

Las tablas de agudeza visual se utilizan durante muchos tipos de exámenes de la vista, como por ejemplo para "refractar" el ojo para determinar la mejor prescripción de anteojos.

La letra más grande de una tabla optométrica suele representar una agudeza visual de 6/60 (20/200), el valor que se considera "legalmente ciego" en los EE. UU. Muchas personas con miopía alta no pueden leer la letra E grande sin anteojos, pero pueden leer la línea 6/6 (20/20) o la línea 6/4.5 (20/15) con anteojos. Por el contrario, las personas legalmente ciegas tienen una agudeza visual de 6/60 (20/200) o menos cuando usan la mejor lente correctiva.

Para garantizar una iluminación adecuada de las tablas de Snellen, varios fabricantes de dispositivos médicos han desarrollado productos de tablas de Snellen con retroiluminación o proyección.

Dado que los monitores de ordenador suelen tener una buena iluminación para leer y los monitores LCD/LED tienen una alta resolución de DPI (entre 96 y 480), son adecuados para mostrar optotipos. Los productos de gráficos digitales suelen permitir la aleatorización de los optotipos que se muestran para evitar que los pacientes memoricen las líneas que ya leyeron. En Google Play y App Store (iOS) hay aplicaciones de gráficos de Snellen para teléfonos inteligentes y tabletas.

Wikimedia Commons alberga una categoría multimedia sobre Diagramas de Snellen .

• Diagrama de Snellen
• Proyector de gráficos
• Acuidad Pro
• Gráficos de agudeza visual
• Validación de un sistema electrónico portátil de agudeza visual