Sistema de clasificación Elo

El sistema de clasificación Elo ^[a] es un método para calcular los niveles de habilidad relativos de los jugadores en juegos de suma cero como el ajedrez o los deportes electrónicos . Recibe su nombre en honor a su creador Arpad Elo , un profesor de física húngaro-estadounidense.

El sistema Elo fue inventado como un sistema de calificación de ajedrez mejorado respecto del sistema Harkness utilizado anteriormente , ^[1] pero también se utiliza como sistema de calificación en fútbol , ​​fútbol americano , béisbol , baloncesto , billar , varios juegos de mesa y deportes electrónicos y, más recientemente, en grandes modelos de lenguaje .

La diferencia de puntuaciones entre dos jugadores sirve como predictor del resultado de un partido. Se espera que dos jugadores con la misma puntuación que se enfrentan obtengan el mismo número de victorias. Se espera que un jugador cuya puntuación sea 100 puntos mayor que la de su oponente obtenga un 64%; si la diferencia es de 200 puntos, la puntuación esperada para el jugador más fuerte es del 76%. ^[2]

La calificación Elo de un jugador es un número que puede cambiar según el resultado de las partidas puntuadas jugadas. Después de cada partida, el jugador ganador le quita puntos al perdedor. La diferencia entre las calificaciones del ganador y el perdedor determina la cantidad total de puntos ganados o perdidos después de una partida. Si el jugador con mayor calificación gana, entonces solo se le quitarán unos pocos puntos de calificación al jugador con menor calificación. Sin embargo, si el jugador con menor calificación logra una victoria inesperada , se transferirán muchos puntos de calificación. El jugador con menor calificación también ganará algunos puntos del jugador con mayor calificación en caso de empate. Esto significa que este sistema de calificación se autocorrige. Los jugadores cuyas calificaciones son demasiado bajas o demasiado altas deberían, a largo plazo, hacerlo mejor o peor de lo que predice el sistema de calificación y, por lo tanto, ganar o perder puntos de calificación hasta que las calificaciones reflejen su verdadera fuerza de juego.

Las clasificaciones Elo son solo comparativas y válidas únicamente dentro del grupo de clasificación en el que se calcularon, en lugar de ser una medida absoluta de la fuerza de un jugador.

Si bien los sistemas tipo Elo se utilizan ampliamente en entornos de dos jugadores, también se han aplicado variaciones a competiciones multijugador. ^[3]

Arpad Elo fue un maestro de ajedrez y un participante activo en la Federación de Ajedrez de los Estados Unidos (USCF) desde su fundación en 1939. ^[4] La USCF utilizó un sistema de clasificación numérica ideado por Kenneth Harkness para permitir a los miembros seguir su progreso individual en términos distintos a las victorias y derrotas en torneos. El sistema de Harkness era razonablemente justo, pero en algunas circunstancias dio lugar a clasificaciones que muchos observadores consideraron inexactas.

En nombre de la USCF, Elo ideó un nuevo sistema con una base estadística más sólida ^{[ aclaración necesaria ]} . ^[5] Casi al mismo tiempo, György Karoly y Roger Cook desarrollaron de forma independiente un sistema basado en los mismos principios para la Asociación de Ajedrez de Nueva Gales del Sur. ^[6]

El sistema de Elo reemplazó los sistemas anteriores de recompensas competitivas por un sistema basado en estimaciones estadísticas. Los sistemas de clasificación de muchos deportes otorgan puntos de acuerdo con evaluaciones subjetivas de la "grandeza" de ciertos logros. Por ejemplo, ganar un torneo de golf importante podría valer cinco veces más puntos que ganar un torneo menor.

Un esfuerzo estadístico, por el contrario, utiliza un modelo que relaciona los resultados del juego con variables subyacentes que representan la habilidad de cada jugador.

El supuesto central de Elo era que el rendimiento de cada jugador en cada partida es una variable aleatoria de distribución normal . Aunque un jugador puede tener un rendimiento significativamente mejor o peor de una partida a la siguiente, Elo suponía que el valor medio del rendimiento de cualquier jugador determinado cambia sólo lentamente con el tiempo. Elo consideraba que la verdadera habilidad de un jugador era la media de la variable aleatoria del rendimiento de ese jugador.

Es necesario hacer otra suposición, ya que el rendimiento en ajedrez en el sentido antes mencionado todavía no es medible. No se puede observar una secuencia de movimientos y derivar un número que represente la habilidad de ese jugador. El rendimiento solo se puede inferir a partir de victorias, empates y derrotas. Por lo tanto, se supone que un jugador que gana una partida ha rendido a un nivel superior al de su oponente en esa partida. Por el contrario, se supone que un jugador perdedor ha rendido a un nivel inferior. Si la partida termina en tablas, se supone que los dos jugadores han rendido a un nivel casi igual.

Elo no especificó exactamente qué tan cercanas deben ser las dos actuaciones para que el resultado sea un empate en lugar de una victoria o una derrota. En realidad, existe una probabilidad de empate que depende de la diferencia de rendimiento, por lo que esta última es más un intervalo de confianza que una frontera determinista. Y aunque pensó que era probable que los jugadores pudieran tener diferentes desviaciones estándar en sus actuaciones, hizo una suposición simplificadora en sentido contrario.

Para simplificar aún más el cálculo, Elo propuso un método sencillo para estimar las variables de su modelo (es decir, la verdadera habilidad de cada jugador). Se podía calcular con relativa facilidad a partir de tablas cuántos juegos se esperaba que ganaran los jugadores en función de comparaciones de sus puntuaciones con las de sus oponentes. Las puntuaciones de un jugador que ganara más juegos de los esperados se ajustarían hacia arriba, mientras que las de un jugador que ganara menos de lo esperado se ajustarían hacia abajo. Además, ese ajuste debía ser linealmente proporcional al número de victorias en las que el jugador había superado o no había alcanzado el número esperado. ^[7]

Desde una perspectiva moderna, las suposiciones simplificadoras de Elo no son necesarias porque la potencia informática es barata y está ampliamente disponible. Varias personas, en particular Mark Glickman , han propuesto utilizar maquinaria estadística más sofisticada para estimar las mismas variables. Por otro lado, la simplicidad computacional del sistema Elo ha demostrado ser una de sus mayores ventajas. Con la ayuda de una calculadora de bolsillo, un competidor de ajedrez informado puede calcular con un margen de error de un punto cuál será su próxima calificación publicada oficialmente, lo que ayuda a promover la percepción de que las calificaciones son justas.

La USCF implementó las sugerencias de Elo en 1960, ^[8] y el sistema rápidamente ganó reconocimiento por ser más justo y más preciso que el sistema de clasificación de Harkness . El sistema de Elo fue adoptado por la Federación Mundial de Ajedrez (FIDE) en 1970. ^[9] Elo describió su trabajo en detalle en The Rating of Chessplayers, Past and Present , publicado por primera vez en 1978. ^[10]

Pruebas estadísticas posteriores han sugerido que el rendimiento en ajedrez casi con certeza no se distribuye como una distribución normal , ya que los jugadores más débiles tienen mayores posibilidades de ganar de lo que predice el modelo de Elo. ^{[11] [12]} En los datos de comparación por pares, a menudo hay muy poca diferencia práctica en si se supone que las diferencias en las fortalezas de los jugadores se distribuyen de manera normal o logística . Sin embargo, matemáticamente, la función logística es más conveniente para trabajar que la distribución normal. ^[13] La FIDE continúa utilizando la tabla de diferencias de calificación propuesta por Elo. ^{[14] : tabla 8.1b}

El desarrollo de la Tabla de Expectativas Porcentuales (tabla 2.11) se describe con más detalle por Elo de la siguiente manera: ^[15]

Las probabilidades normales se pueden tomar directamente de las tablas estándar de las áreas bajo la curva normal cuando la diferencia en la calificación se expresa como una puntuación z. Dado que la desviación estándar σ de los rendimientos individuales se define como 200 puntos, la desviación estándar σ' de las diferencias en los rendimientos se convierte en σ√2 o 282,84. El valor z de una diferencia es entonces D / 282,84 . Esto dividirá el área bajo la curva en dos partes, la más grande da P para el jugador con mayor calificación y la más pequeña da P para el jugador con menor calificación.

Por ejemplo, supongamos que D = 160. Entonces, z = 160 / 282,84 = 0,566 . La tabla indica 0,7143 y 0,2857 como áreas de las dos partes bajo la curva. Estas probabilidades se redondean a dos cifras en la tabla 2.11.

La tabla en realidad está construida con una desviación estándar de 200(10/7) como aproximación para 200√2 . ^{[ cita requerida ]}

Las distribuciones normal y logística son, en cierto modo, puntos arbitrarios en un espectro de distribuciones que funcionarían bien. En la práctica, ambas distribuciones funcionan muy bien para varios juegos diferentes. ^{[ cita requerida ]}

La frase "puntuación Elo" se utiliza a menudo para referirse a la puntuación de ajedrez de un jugador calculada por la FIDE. Sin embargo, este uso puede ser confuso o engañoso porque las ideas generales de Elo han sido adoptadas por muchas organizaciones, incluida la USCF (antes de la FIDE), muchas otras federaciones nacionales de ajedrez, la efímera Asociación Profesional de Ajedrez (PCA) y servidores de ajedrez en línea, incluidos el Internet Chess Club (ICC), Free Internet Chess Server (FICS), Lichess , Chess.com y Yahoo! Games. Cada organización tiene una implementación única y ninguna de ellas sigue las sugerencias originales de Elo con precisión.

En su lugar, se puede hacer referencia a la organización que otorga la calificación. Por ejemplo: "En abril de 2018, Tatev Abrahamyan tenía una calificación FIDE de 2366 y una calificación USCF de 2473". Las calificaciones Elo de estas diversas organizaciones no siempre son directamente comparables, ya que las calificaciones Elo miden los resultados dentro de un grupo cerrado de jugadores en lugar de la habilidad absoluta.

Para los mejores jugadores, la clasificación más importante es la clasificación FIDE . La FIDE ha publicado las siguientes listas:

• Desde 1971 a 1980 se publicó una lista por año.
• De 1981 a 2000 se publicaron dos listas al año, en enero y julio.
• Desde julio de 2000 a julio de 2009 se publicaron cuatro listas al año, a principios de enero, abril, julio y octubre.
• Desde julio de 2009 a julio de 2012 se publicaron seis listas al año, a principios de enero, marzo, mayo, julio, septiembre y noviembre.
• Desde julio de 2012, la lista se actualiza mensualmente.

El siguiente análisis de la lista de clasificación FIDE de julio de 2015 da una idea aproximada de lo que significa una clasificación FIDE determinada en términos de clasificación mundial:

• 5.323 jugadores tenían una calificación activa en el rango de 2200 a 2299, que generalmente se asocia con el título de Candidato a Maestro .
• 2.869 jugadores tenían una calificación activa en el rango de 2300 a 2399, que generalmente se asocia con el título de Maestro FIDE .
• 1.420 jugadores tenían una calificación activa entre 2400 y 2499, la mayoría de los cuales tenían el título de Maestro Internacional o Gran Maestro Internacional .
• 542 jugadores tenían una calificación activa entre 2500 y 2599, la mayoría de los cuales tenían el título de Gran Maestro Internacional .
• 187 jugadores tenían una calificación activa entre 2600 y 2699, todos ellos con el título de Gran Maestro Internacional .
• 40 jugadores tenían una calificación activa entre 2700 y 2799.
• 4 jugadores tuvieron una calificación activa de más de 2800. ( Magnus Carlsen tuvo una calificación de 2853 y 3 jugadores tuvieron una calificación entre 2814 y 2816).

La calificación FIDE más alta de la historia fue 2882, y la obtuvo Magnus Carlsen en la lista de mayo de 2014. En Comparación de los mejores ajedrecistas de la historia se puede encontrar una lista de los jugadores con la calificación más alta de la historia .

${\estilo de visualización p}$	$estilo de visualización d_{p}}$
1.00	+800
0,99	+677
0.9	+366
0,8	+240
0,7	+149
0.6	+72
0,5	0
0,4	-72
0.3	−149
0,2	-240
0,1	−366
0,01	−677
0.00	−800

La calificación de rendimiento o calificación especial es una calificación hipotética que resultaría de las partidas de un solo evento. Algunas organizaciones de ajedrez ^{[16] : p. 8} utilizan el "algoritmo de 400" para calcular la calificación de rendimiento. Según este algoritmo, la calificación de rendimiento para un evento se calcula de la siguiente manera:

1. Por cada victoria, suma la calificación de tu oponente más 400,
2. Por cada derrota, suma la calificación de tu oponente menos 400,
3. Y divide esta suma por el número de juegos jugados.

Ejemplo: 2 victorias (oponentes w y x ), 2 derrotas (oponentes y y z )

${\displaystyle {\begin{aligned}&{\frac {w+400+x+400+y-400+z-400}{4}}\\[6pt]&{\frac {w+x+y+z+400(2)-400(2)}{4}}\end{aligned}}}$

Esto puede expresarse mediante la siguiente fórmula:

${\displaystyle {\text{calificación de rendimiento}}={\frac {{\text{total de calificaciones de los oponentes}}+400\times ({\text{victorias}}-{\text{derrotas}})}{\text{juegos}}}}$

Ejemplo: Si vences a un jugador con una puntuación Elo de 1000,

${\displaystyle {\text{calificación de rendimiento}}={\frac {1000+400\times (1)}{1}}=1400}$

Si vences a dos jugadores con una puntuación Elo de 1000,

${\displaystyle {\text{calificación de rendimiento}}={\frac {2000+400\times (2)}{2}}=1400}$

Si dibujas,

${\displaystyle {\text{calificación de rendimiento}}={\frac {1000+400\times (0)}{1}}=1000}$

Esta es una simplificación, pero ofrece una forma fácil de obtener una estimación de PR (clasificación de desempeño).

La FIDE , sin embargo, calcula la calificación de rendimiento mediante la fórmula donde la "diferencia de calificación" se basa en el puntaje porcentual del torneo de un jugador , que luego se utiliza como clave en una tabla de búsqueda donde es simplemente la cantidad de puntos anotados dividido por la cantidad de partidas jugadas. Tenga en cuenta que, en caso de un puntaje perfecto o nulo, es 800.$${\displaystyle {\text{calificación de rendimiento}}={\text{promedio de las calificaciones de los oponentes}}+d_{p},}$$$estilo de visualización d_{p}}$${\estilo de visualización p}$${\estilo de visualización p}$$estilo de visualización d_{p}}$

La FIDE actualiza su lista de clasificaciones a principios de cada mes. En cambio, las "clasificaciones en vivo" no oficiales calculan el cambio en las clasificaciones de los jugadores después de cada partida. Estas clasificaciones en vivo se basan en las clasificaciones de la FIDE publicadas previamente, por lo que la clasificación en vivo de un jugador tiene como objetivo corresponder a la clasificación que tendría la FIDE si la FIDE publicara una nueva lista ese día.

Aunque las clasificaciones en vivo no son oficiales, el interés en las clasificaciones en vivo surgió en agosto/septiembre de 2008 cuando cinco jugadores diferentes ocuparon el puesto número 1 del ranking "en vivo". ^[17]

Las clasificaciones en vivo no oficiales de jugadores de más de 2700 fueron publicadas y mantenidas por Hans Arild Runde en el sitio web Live Rating hasta agosto de 2011. Otro sitio web, 2700chess.com, ha sido mantenido desde mayo de 2011 por Artiom Tsepotan , que cubre a los 100 mejores jugadores, así como a las 50 mejores jugadoras.

Los cambios de calificación se pueden calcular manualmente utilizando la calculadora de cambios de calificación de la FIDE. ^[18] Todos los mejores jugadores tienen un factor K de 10, lo que significa que el cambio de calificación máximo en una sola partida es un poco menos de 10 puntos.

La Federación de Ajedrez de los Estados Unidos (USCF) utiliza su propia clasificación de jugadores: ^[19]

• 2400 y más: Máster sénior
• 2200–2399: Maestro Nacional
  • 2200–2399 más 300 juegos por encima de 2200: Original Life Master ^[20]
• 2000–2199: Experto o Candidato a Maestro
• 1800–1999: Clase A
• 1600–1799: Clase B
• 1400–1599: Clase C
• 1200–1399: Clase D
• 1000–1199: Clase E
• 800–999: Clase F
• 600–799: Clase G
• 400–599: Clase H
• 200–399: Clase I
• 100–199: Clase J

El factor K , en el sistema de clasificación USCF, se puede estimar dividiendo 800 por la cantidad efectiva de juegos en los que se basa la clasificación de un jugador ( N _​​e ) más la cantidad de juegos que el jugador completó en un torneo ( m ). ^[21]

${\displaystyle K={\frac {800}{N_{e}+m}}\,}$

La USCF mantiene un nivel de calificación absoluto de 100 para todas las clasificaciones. Por lo tanto, ningún miembro puede tener una calificación inferior a 100, sin importar su desempeño en eventos sancionados por la USCF. Sin embargo, los jugadores pueden tener niveles de calificación absolutos individuales más altos, calculados mediante la siguiente fórmula:

${\displaystyle AF=\operatorname {min} \{100+4N_{W}+2N_{D}+N_{R},150\}}$

donde es el número de juegos calificados ganados, es el número de juegos calificados empatados y es el número de eventos en los que el jugador completó tres o más juegos calificados.${\displaystyle N_{W}}$$Estilo de visualización N_ {D}}$$Estilo de visualización N_{R}$

Existen niveles de calificación más altos para los jugadores experimentados que han alcanzado calificaciones significativas. Dichos niveles de calificación más altos existen a partir de calificaciones de 1200 en incrementos de 100 puntos hasta 2100 (1200, 1300, 1400, ..., 2100). Un nivel de calificación se calcula tomando la calificación máxima establecida del jugador, restándole 200 puntos y luego redondeando hacia abajo al nivel de calificación más cercano. Por ejemplo, un jugador que ha alcanzado una calificación máxima de 1464 tendría un nivel de calificación de 1464 − 200 = 1264 , que se redondearía hacia abajo a 1200. Bajo este esquema, solo los jugadores de Clase C y superiores pueden tener un nivel de calificación más alto que su calificación absoluta de jugador. Todos los demás jugadores tendrían un nivel de calificación de 150 como máximo.

Existen dos formas de alcanzar niveles de calificación más altos además del esquema estándar presentado anteriormente. Si un jugador ha alcanzado la calificación de Original Life Master, su nivel de calificación se establece en 2200. La obtención de este título es única, ya que ningún otro título reconocido por la USCF dará lugar a un nuevo nivel de calificación. Para los jugadores con calificaciones inferiores a 2000, ganar un premio en efectivo de $2000 o más eleva el nivel de calificación de ese jugador al nivel de 100 puntos más cercano que lo hubiera descalificado para participar en el torneo. Por ejemplo, si un jugador ganó $4000 en un torneo de 1750 o menos, ahora tendría un nivel de calificación de 1800.

Las comparaciones por pares forman la base de la metodología de calificación Elo. ^[22] Elo hizo referencia a los artículos de Good, ^[23] David, ^[24] Trawinski y David, ^[25] y Buhlman y Huber. ^[26]

El rendimiento no se mide de forma absoluta; se infiere de las victorias, derrotas y empates contra otros jugadores. Las calificaciones de los jugadores dependen de las calificaciones de sus oponentes y de los resultados que obtienen contra ellos. La diferencia de calificación entre dos jugadores determina una estimación de la puntuación esperada entre ellos. Tanto la media como la diferencia de calificaciones se pueden elegir de forma arbitraria. La USCF inicialmente tenía como objetivo que un jugador de club medio tuviera una calificación de 1500 y Elo sugirió escalar las calificaciones de modo que una diferencia de 200 puntos de calificación en ajedrez significara que el jugador más fuerte tiene una puntuación esperada de aproximadamente 0,75.

La puntuación esperada de un jugador es su probabilidad de ganar más la mitad de su probabilidad de empatar. Por lo tanto, una puntuación esperada de 0,75 podría representar un 75 % de posibilidades de ganar, un 25 % de posibilidades de perder y un 0 % de posibilidades de empatar. En el otro extremo, podría representar un 50 % de posibilidades de ganar, un 0 % de posibilidades de perder y un 50 % de posibilidades de empatar. La probabilidad de empatar, a diferencia de la de tener un resultado decisivo, no está especificada en el sistema Elo. En cambio, un empate se considera la mitad de una victoria y la otra mitad de una derrota. En la práctica, dado que se desconoce la verdadera fuerza de cada jugador, las puntuaciones esperadas se calculan utilizando las calificaciones actuales del jugador de la siguiente manera.

Si el jugador  A tiene una calificación de y el jugador  B una calificación de , la fórmula exacta (usando la curva logística con base 10 ) ^[27] para la puntuación esperada del jugador  A es${\displaystyle \,R_{\mathsf {A}}\,}$${\displaystyle \,R_{\mathsf {B}}\,}$

${\displaystyle E_{A}}={\frac {1}{1+10^{(R_{B}}-R_{A}})/400}}}~.}$

De manera similar, la puntuación esperada para el jugador  B es

${\displaystyle E_{\mathsf {B}}={\frac {1}{1+10^{(R_{\mathsf {A}}-R_{\mathsf {B}})/400}}}~.}$

Esto también podría expresarse por

${\displaystyle E_{\mathsf {A}}={\frac {Q_{\mathsf {A}}}{Q_{\mathsf {A}}+Q_{\mathsf {B}}}}}$

y

${\displaystyle E_{\mathsf {B}}={\frac {Q_{\mathsf {B}}}{Q_{\mathsf {A}}+Q_{\mathsf {B}}}}~,}$

donde y Nótese que en el último caso, el mismo denominador se aplica a ambas expresiones, y es evidente que Esto significa que al estudiar solo los numeradores, descubrimos que la puntuación esperada para el jugador  A es veces la puntuación esperada para el jugador  B. Luego se deduce que por cada 400 puntos de calificación de ventaja sobre el oponente, la puntuación esperada se magnifica diez veces en comparación con la puntuación esperada del oponente.${\displaystyle \;Q_{\mathsf {A}}=10^{R_{\mathsf {A}}/400}\;,}$${\displaystyle \;Q_{\mathsf {B}}=10^{R_{\mathsf {B}}/400}~.}$${\displaystyle \;E_{\mathsf {A}}+E_{\mathsf {B}}=1~.}$${\displaystyle \;Q_{\mathsf {A}}/Q_{\mathsf {B}}\;}$

Cuando las puntuaciones reales de un jugador en un torneo superan las puntuaciones esperadas, el sistema Elo lo considera una prueba de que la calificación del jugador es demasiado baja y debe ajustarse hacia arriba. De manera similar, cuando las puntuaciones reales de un jugador en un torneo no alcanzan las puntuaciones esperadas, la calificación de ese jugador se ajusta hacia abajo. La sugerencia original de Elo, que todavía se usa ampliamente, era un simple ajuste lineal proporcional a la cantidad en que un jugador superaba o no superaba la puntuación esperada. El ajuste máximo posible por juego, llamado factor K, se estableció para los maestros y para los jugadores más débiles.${\displaystyle \;K=16\;}$${\displaystyle \;K=32\;}$

Supongamos que se esperaba que el jugador  A (de nuevo con calificación ) anotara puntos, pero en realidad los anotó. La fórmula para actualizar la calificación de ese jugador es${\displaystyle R_{\mathsf {A}}}$${\displaystyle \,E_{\mathsf {A}}\,}$${\displaystyle \,S_{\mathsf {A}}\,}$

${\displaystyle R_{A}}'=R_{A}}+K\cdot (S_{A}}-E_{A}})~.}$^[1]

Esta actualización se puede realizar después de cada juego o de cada torneo, o después de cualquier período de clasificación adecuado.

Un ejemplo puede ayudar a aclararlo:

Supongamos que el jugador  A tiene una puntuación de 1613 y juega en un torneo de cinco rondas. Pierde contra un jugador con una puntuación de 1609, empata con un jugador con una puntuación de 1477, derrota a un jugador con una puntuación de 1388, derrota a un jugador con una puntuación de 1586 y pierde contra un jugador con una puntuación de 1720. La puntuación real del jugador es (0 + 0,5 + 1 + 1 + 0) = 2,5 . La puntuación esperada, calculada según la fórmula anterior, era (0,51 + 0,69 + 0,79 + 0,54 + 0,35) = 2,88 .

Por lo tanto, la nueva calificación del jugador es [1613 + 32·(2.5 − 2.88)] = 1601 , asumiendo que se usa un factor K de 32. De manera equivalente, en cada juego se puede decir que el jugador ha puesto una apuesta inicial de K veces su puntaje esperado para el juego en un bote, el jugador oponente hace lo mismo y el ganador se lleva el bote completo de valor K ; en caso de empate, los jugadores se dividen el bote y reciben puntos cada uno.${\displaystyle \;{\tfrac {1}{2}}K\;}$

Tenga en cuenta que, si bien dos victorias, dos derrotas y un empate pueden parecer una puntuación normal, es peor de lo esperado para el jugador  A porque sus oponentes tenían una puntuación media inferior. Por lo tanto, el jugador  A recibe una ligera penalización. Si el jugador  A hubiera obtenido dos victorias, una derrota y dos empates, para una puntuación total de tres puntos, eso habría sido ligeramente mejor de lo esperado, y la nueva puntuación del jugador habría sido [1613 + 32·(3 − 2.88)] = 1617 .

Este procedimiento de actualización es la base de las clasificaciones utilizadas por la FIDE , la USCF , Yahoo! Games , el Internet Chess Club (ICC) y el Free Internet Chess Server (FICS). Sin embargo, cada organización ha adoptado un enfoque diferente para abordar la incertidumbre inherente a las clasificaciones, en particular las clasificaciones de los recién llegados, y para abordar el problema de la inflación/deflación de las clasificaciones. A los nuevos jugadores se les asignan clasificaciones provisionales, que se ajustan de forma más drástica que las clasificaciones establecidas.

Los principios utilizados en estos sistemas de clasificación se pueden utilizar para clasificar otras competiciones, por ejemplo, partidos de fútbol internacionales.

Las clasificaciones Elo también se han aplicado a juegos sin posibilidad de empate y a juegos en los que el resultado puede tener una cantidad (pequeño/grande margen) además de la calidad (victoria/derrota). Consulta la clasificación Elo de Go para obtener más información.

En 2011, después de analizar 1,5 millones de partidas con puntuación FIDE, Jeff Sonas demostró que, según la fórmula Elo, dos jugadores que tienen una diferencia de puntuación de X en realidad tienen una diferencia real de alrededor de X (5/6) . Del mismo modo, uno puede dejar la diferencia de puntuación sola y dividir por 480 en lugar de 400. Dado que la fórmula Elo sobreestima la probabilidad de victoria del jugador más fuerte, los jugadores más fuertes pierden puntos contra jugadores más débiles a pesar de jugar con su verdadera fuerza. Del mismo modo, los jugadores más débiles ganan puntos contra jugadores más fuertes. Cuando se aplica la modificación, las tasas de victoria observadas se desvían en menos del 0,1% de la predicción, mientras que el Elo tradicional puede estar un 4% por debajo de la tasa predicha. ^[28]

La primera preocupación matemática que abordó la USCF fue el uso de la distribución normal . Descubrieron que esta no representaba con precisión los resultados reales obtenidos, en particular por los jugadores con menor puntuación. En su lugar, cambiaron a un modelo de distribución logística , que la USCF consideró que se ajustaba mejor a los resultados reales obtenidos. ^{[29] [ cita requerida ]} La FIDE también utiliza una aproximación a la distribución logística. ^[14]

La segunda preocupación importante es el uso correcto del " factor K ". El estadístico de ajedrez Jeff Sonas cree que el valor original (para jugadores con una puntuación superior a 2400) es inexacto en el trabajo de Elo. Si el coeficiente del factor K se establece demasiado alto, habrá demasiada sensibilidad a sólo unos pocos eventos recientes, en términos de una gran cantidad de puntos intercambiados en cada partida. Y si el valor K es demasiado bajo, la sensibilidad será mínima y el sistema no responderá con la suficiente rapidez a los cambios en el nivel real de rendimiento de un jugador.${\displaystyle \;K=10\;}$

La estimación original del factor K de Elo se realizó sin el beneficio de grandes bases de datos ni evidencia estadística. Sonas indica que un factor K de 24 (para jugadores con una puntuación superior a 2400) puede ser más preciso como herramienta predictiva del rendimiento futuro y ser más sensible al rendimiento. ^[30]

Algunos sitios de ajedrez en Internet parecen evitar un escalonamiento del factor K de tres niveles basado en el rango de puntuación. Por ejemplo, el ICC parece adoptar un factor K global de 32 , excepto cuando se juega contra jugadores con puntuación provisional.

La USCF (que utiliza una distribución logística en lugar de una distribución normal ) anteriormente escalonaba el factor K según tres rangos de calificación principales:

Factor   K	Se utiliza para jugadores con calificaciones...
${\displaystyle \;K=32\;}$	por debajo de 2100
${\displaystyle \;K=24\;}$	Entre 2100 y 2400
${\displaystyle \;K=16\;}$	por encima de 2400

Actualmente, la USCF utiliza una fórmula que calcula el factor K en función de factores como la cantidad de juegos jugados y la calificación del jugador. El factor K también se reduce para los jugadores con calificaciones altas si el evento tiene controles de tiempo más cortos. ^[16]

La FIDE utiliza los siguientes rangos: ^[31]

Factor   K	Se utiliza para jugadores con calificaciones...
${\displaystyle \;K=40\;}$	para un jugador nuevo en la lista de clasificación hasta la finalización de eventos con un total de 30 juegos, y para todos los jugadores hasta su cumpleaños número 18, siempre que su clasificación se mantenga por debajo de 2300.
${\displaystyle \;K=20\;}$	Para jugadores que siempre han tenido una puntuación inferior a 2400.
${\displaystyle \;K=10\;}$	para jugadores con una calificación publicada de al menos 2400 y al menos 30 partidas jugadas en eventos anteriores. A partir de entonces, se mantiene permanentemente en 10.

La FIDE utilizó los siguientes rangos antes de julio de 2014: ^[32]

Factor   K	Se utiliza para jugadores con calificaciones...
${\displaystyle \;K=30\;}$ (tenía 25)	para un jugador nuevo en la lista de clasificación hasta la finalización de los eventos con un total de 30 juegos. [33]
${\displaystyle \;K=15\;}$	Para jugadores que siempre han tenido una puntuación inferior a 2400.
${\displaystyle \;K=10\;}$	para jugadores con una calificación publicada de al menos 2400 y al menos 30 partidas jugadas en eventos anteriores. A partir de entonces, se mantiene permanentemente en 10.

La gradación del factor K reduce el cambio de calificación en el extremo superior del rango de calificación, lo que reduce la posibilidad de un aumento o caída rápida de la calificación para aquellos con una calificación lo suficientemente alta como para alcanzar un factor K bajo .

En teoría, esto podría aplicarse igualmente a los jugadores de ajedrez en línea y a los jugadores presenciales, ya que es más difícil para todos los jugadores aumentar su calificación después de que su calificación se ha vuelto alta y su factor K en consecuencia se ha reducido. Sin embargo, cuando se juega en línea, los jugadores de 2800+ pueden aumentar su calificación más fácilmente simplemente seleccionando oponentes con calificaciones altas: en el sitio de juego de ICC, un gran maestro puede jugar con una serie de oponentes diferentes que tengan una calificación superior a 2700. ^[34] En los eventos presenciales, solo sería en eventos de todos contra todos de muy alto nivel que un jugador podría enfrentarse a esa cantidad de oponentes de 2700+. En un torneo de ajedrez normal, abierto, con emparejamientos suizos, con frecuencia habría muchos oponentes con una calificación inferior a 2500, lo que reduce las ganancias de calificación posibles de una sola competencia para un jugador de alta calificación.

Las expresiones anteriores pueden derivarse formalmente ahora explotando el vínculo entre la calificación Elo y la actualización del gradiente estocástico en la regresión logística. ^{[35] [36]}

Si asumimos que los resultados del juego son binarios , es decir, solo se puede observar una victoria o una derrota, el problema se puede abordar mediante regresión logística , donde los resultados del juego son variables dependientes , las calificaciones de los jugadores son variables independientes y el modelo que relaciona ambas es probabilístico: la probabilidad de que el jugador gane el juego se modela como${\displaystyle {\mathsf {A}}}$

${\displaystyle \Pr\{{\mathsf {A}}~{\textrm {gana}}\}=\sigma (r_{\mathsf {A,B}}),\quad \sigma (r)={\frac {1}{1+10^{-r/s}}},}$

dónde

${\displaystyle r_{A,B}}=(R_{A-R_{B)}$

denota la diferencia de las calificaciones de los jugadores, y utilizamos un factor de escala y, por la ley de probabilidad total${\estilo de visualización s=400}$

${\displaystyle \Pr\{{\mathsf {B}}~{\textrm {gana}}\}=1-\sigma (r_{\mathsf {A,B}})=\sigma (-r_{\mathsf {A,B}}).}$

La pérdida logarítmica se calcula entonces como

${\displaystyle \ell ={\begin{cases}-\log \sigma (r_{\mathsf {A,B}})&{\textrm {si}}~{\mathsf {A}}~{\textrm {gana}},\\-\log \sigma (-r_{\mathsf {A,B}})&{\textrm {si}}~{\mathsf {B}}~{\textrm {gana}},\end{cases}}}$

y, utilizando el descenso de gradiente estocástico, la pérdida logarítmica se minimiza de la siguiente manera:

${\displaystyle R_{\mathsf {A}}\leftarrow R_{\mathsf {A}}-\eta {\frac {{\textrm {d}}\ell }{{\textrm {d}}R_{\mathsf {A}}}}}$,

${\displaystyle R_{\mathsf {B}}\leftarrow R_{\mathsf {B}}-\eta {\frac {{\textrm {d}}\ell }{{\textrm {d}}R_{\mathsf {B}}}}}$.

¿Dónde está el paso de adaptación?${\displaystyle \eta }$

Dado que , , y , la adaptación se escribe entonces de la siguiente manera${\displaystyle {\frac {\textrm {d}}{{\textrm {d}}r}}\log \sigma (r)={\frac {\log 10}{s}}\sigma (-r)}$${\displaystyle {\frac {{\textrm {d}}r_{\mathsf {A,B}}}{{\textrm {d}}R_{\mathsf {A}}}}=1}$${\displaystyle {\frac {{\textrm {d}}r_{\mathsf {A,B}}}{{\textrm {d}}R_{\mathsf {B}}}}=-1}$

${\displaystyle R_{\mathsf {A}}\leftarrow {\begin{cases}R_{\mathsf {A}}+K\sigma (-r_{\mathsf {A,B}})&{\textrm {if}}~{\mathsf {A}}~{\textrm {wins}}\\R_{\mathsf {A}}-K\sigma (r_{\mathsf {A,B}})&{\textrm {if}}~{\mathsf {B}}~{\textrm {wins}},\end{cases}}}$

que puede escribirse de forma compacta como

${\displaystyle R_{\mathsf {A}}\leftarrow R_{\mathsf {A}}+K(S_{\mathsf {A}}-E_{\mathsf {A}})}$

¿Dónde está el nuevo paso de adaptación que absorbe y , si gana y si gana, y el puntaje esperado está dado por .${\displaystyle K=\eta \log 10/s}$${\displaystyle \eta }$${\displaystyle s}$${\displaystyle S_{\mathsf {A}}=1}$${\displaystyle {\mathsf {A}}}$${\displaystyle S_{\mathsf {A}}=0}$${\displaystyle {\mathsf {B}}}$${\displaystyle E_{\mathsf {A}}=\sigma (r_{\mathsf {A,B}})}$

De manera análoga, la actualización de la calificación es${\displaystyle R_{\mathsf {B}}}$

${\displaystyle R_{\mathsf {B}}\leftarrow R_{\mathsf {B}}+K(S_{\mathsf {B}}-E_{\mathsf {B}})}$.

Desde el principio, la puntuación Elo también se ha utilizado en ajedrez, donde observamos victorias, derrotas o empates y, para tratar estos últimos, se introduce un valor de puntuación fraccionaria, . Sin embargo, observamos que las puntuaciones y son simplemente indicadores de los eventos cuando el jugador gana o pierde la partida. Por lo tanto, no está inmediatamente claro cuál es el significado de la puntuación fraccionaria. Además, dado que no especificamos explícitamente el modelo que relaciona los valores de la puntuación y con la probabilidad del resultado de la partida, no podemos decir cuál es la probabilidad de la victoria, la derrota o el empate.${\displaystyle S_{\mathsf {A}}=0.5}$${\displaystyle S_{\mathsf {A}}=1}$${\displaystyle S_{\mathsf {A}}=0}$${\displaystyle {\mathsf {A}}}$${\displaystyle R_{\mathsf {A}}}$${\displaystyle R_{\mathsf {B}}}$

Para abordar estas dificultades y obtener la calificación Elo en los juegos ternarios, definiremos el modelo probabilístico explícito de los resultados. A continuación, minimizaremos la pérdida de registro mediante un gradiente estocástico.

Como la derrota, el empate y la victoria son variables ordinales , debemos adoptar el modelo que tenga en cuenta su naturaleza ordinal, y utilizamos el llamado modelo de categorías adyacentes, cuyo origen se remonta al trabajo de Davidson ^[37].

${\displaystyle \Pr\{{\mathsf {A}}~{\textrm {wins}}\}=\sigma (r_{\mathsf {A,B}};\kappa ),}$

${\displaystyle \Pr\{{\mathsf {B}}~{\textrm {wins}}\}=\sigma (-r_{\mathsf {A,B}};\kappa ),}$

${\displaystyle \Pr\{{\mathsf {A}}~{\textrm {draws}}\}=\kappa {\sqrt {\sigma (r_{\mathsf {A,B}};\kappa )\sigma (-r_{\mathsf {A,B}};\kappa )}},}$

dónde

${\displaystyle \sigma (r;\kappa )={\frac {10^{r/s}}{10^{-r/s}+\kappa +10^{r/s}}}}$

y es un parámetro. La introducción de un parámetro libre no debería sorprendernos, ya que tenemos tres resultados posibles y, por lo tanto, debería aparecer un grado adicional de libertad en el modelo. En particular, con recuperamos el modelo subyacente a la regresión logística${\displaystyle \kappa \geq 0}$${\displaystyle \kappa =0}$

${\displaystyle \Pr\{{\mathsf {A}}~{\textrm {wins}}\}=\sigma (r_{\mathsf {A,B}};0)={\frac {10^{r_{\mathsf {A,B}}/s}}{10^{-r_{\mathsf {A,B}}/s}+10^{r_{\mathsf {A,B}}/s}}}={\frac {1}{1+10^{-r_{\mathsf {A,B}}/s'}}},}$

dónde .${\displaystyle s'=s/2}$

Utilizando el modelo ordinal definido anteriormente, la pérdida logarítmica ahora se calcula como

${\displaystyle \ell ={\begin{cases}-\log \sigma (r_{\mathsf {A,B}};\kappa )&{\textrm {if}}~{\mathsf {A}}~{\textrm {wins}},\\-\log \sigma (-r_{\mathsf {A,B}};\kappa )&{\textrm {if}}~{\mathsf {B}}~{\textrm {wins}},\\-\log \kappa -{\frac {1}{2}}\log \sigma (r_{\mathsf {A,B}};\kappa )-{\frac {1}{2}}\log \sigma (-r_{\mathsf {A,B}};\kappa )&{\textrm {if}}~{\mathsf {A}}~{\textrm {draw}},\end{cases}}}$

que puede escribirse de forma compacta como

${\displaystyle \ell =-(S_{\mathsf {A}}+{\frac {1}{2}}D)\log \sigma (r_{\mathsf {A,B}};\kappa )-(S_{\mathsf {B}}+{\frac {1}{2}}D)\log \sigma (-r_{\mathsf {A,B}};\kappa )-D\log \kappa }$

donde iff gana, iff gana y iff empata.${\displaystyle S_{\mathsf {A}}=1}$ ${\displaystyle {\mathsf {A}}}$${\displaystyle S_{\mathsf {B}}=1}$${\displaystyle {\mathsf {B}}}$${\displaystyle D=1}$${\displaystyle {\mathsf {A}}}$

Como antes, necesitamos la derivada de la cual está dada por${\displaystyle \log \sigma (r;\kappa )}$

${\displaystyle {\frac {\textrm {d}}{{\textrm {d}}r}}\log \sigma (r;\kappa )={\frac {2\log 10}{s}}[1-g(r;\kappa )]}$,

dónde

${\displaystyle g(r;\kappa )={\frac {10^{r/s}+\kappa /2}{10^{-r/s}+\kappa +10^{r/s}}}.}$

Por lo tanto, la derivada de la pérdida logarítmica con respecto a la calificación viene dada por${\displaystyle R_{\mathsf {A}}}$

${\displaystyle {\begin{aligned}{\frac {\textrm {d}}{{\textrm {d}}R_{\mathsf {A}}}}\ell &=-{\frac {2\log 10}{s}}\left((S_{\mathsf {A}}+0.5D)[1-g(r_{\mathsf {A,B}};\kappa )]-(S_{\mathsf {B}}+0.5D)g(r_{\mathsf {A,B}};\kappa )\right)\\&=-{\frac {2\log 10}{s}}\left(S_{\mathsf {A}}+0.5D-g(r_{\mathsf {A,B}};\kappa )\right),\end{aligned}}}$

donde utilizamos las relaciones y .${\displaystyle S_{\mathsf {A}}+S_{\mathsf {B}}+D=1}$${\displaystyle g(-r;\kappa )=1-g(r;\kappa )}$

Luego, el descenso del gradiente estocástico aplicado para minimizar la pérdida de registro produce la siguiente actualización para la calificación${\displaystyle R_{\mathsf {A}}}$

${\displaystyle R_{\mathsf {A}}\leftarrow R_{\mathsf {A}}+K({\hat {S}}_{\mathsf {A}}-g(r_{\mathsf {A,B}};\kappa ))}$

donde y . Por supuesto, si gana, si empata y si pierde. Para reconocer el origen en el modelo propuesto por Davidson, esta actualización se denomina calificación Elo-Davidson. ^[36]${\displaystyle K=2\eta \log 10/s}$${\displaystyle {\hat {S}}_{\mathsf {A}}=S_{\mathsf {A}}+0.5D}$${\displaystyle {\hat {S}}_{\mathsf {A}}=1}$${\displaystyle {\textsf {A}}}$${\displaystyle {\hat {S}}_{\mathsf {A}}=0.5}$${\displaystyle {\textsf {A}}}$${\displaystyle {\hat {S}}_{\mathsf {A}}=0}$${\displaystyle {\textsf {A}}}$

La actualización se deriva de la misma manera que${\displaystyle R_{\mathsf {B}}}$

${\displaystyle R_{\mathsf {B}}\leftarrow R_{\mathsf {B}}+K({\hat {S}}_{\mathsf {B}}-g(r_{\mathsf {B,A}};\kappa ))}$,

dónde .${\displaystyle r_{\mathsf {B,A}}=R_{\mathsf {B}}-R_{\mathsf {A}}=-r_{\mathsf {A,B}}}$

Observamos que

${\displaystyle {\begin{aligned}E[{\hat {S}}_{\mathsf {A}}]&=\Pr\{{\mathsf {A}}~{\text{wins}}\}+0.5\Pr\{{\mathsf {A}}~{\text{draws}}\}\\&=\sigma (r_{\mathsf {A,B}};\kappa )+0.5\kappa {\sqrt {\sigma (r_{\mathsf {A,B}};\kappa )\sigma (-r_{\mathsf {A,B}};\kappa )}}\\&=g(r_{\mathsf {A,B}};\kappa )\end{aligned}}}$

y así obtenemos que la actualización de la calificación puede escribirse como

${\displaystyle R_{\mathsf {A}}\leftarrow R_{\mathsf {A}}+K({\hat {S}}_{\mathsf {A}}-E_{\mathsf {A}})}$,

donde y obtuvimos prácticamente la misma ecuación que en la calificación Elo excepto que la puntuación esperada viene dada por en lugar de .${\displaystyle E_{\mathsf {A}}=E[{\hat {S}}_{\mathsf {A}}]}$${\displaystyle E_{\mathsf {A}}=g(r_{\mathsf {A,B}};\kappa )}$${\displaystyle E_{\mathsf {A}}=\sigma (r_{\mathsf {A,B}})}$

Por supuesto, como se señaló anteriormente, para , tenemos y, por lo tanto, la calificación Elo-Davidson es exactamente la misma que la calificación Elo. Sin embargo, esto no ayuda a comprender el caso cuando se observan los empates (no podemos usar lo que significaría que la probabilidad de empate es nula). Por otro lado, si usamos , tenemos${\displaystyle \kappa =0}$${\displaystyle g(r;0)=\sigma (r)}$${\displaystyle \kappa =0}$${\displaystyle \kappa =2}$

${\displaystyle g(r;2)={\frac {10^{r/s}+1}{10^{-r/s}+2+10^{r/s}}}={\frac {1}{1+10^{-r/s}}}=\sigma (r)}$

lo que significa que, utilizando , la calificación Elo-Davidson es exactamente la misma que la calificación Elo. ^[36]${\displaystyle \kappa =2}$

En algunos casos, el sistema de clasificación puede desalentar la actividad de juego de los jugadores que desean proteger su clasificación. ^[38] Para disuadir a los jugadores de tener una clasificación alta, una propuesta de 2012 del Gran Maestro británico John Nunn para elegir a los clasificados para el campeonato mundial de ajedrez incluía una bonificación por actividad, que se combinaría con la clasificación. ^[39]

Más allá del mundo del ajedrez, las preocupaciones sobre los jugadores que evitaban el juego competitivo para proteger sus calificaciones hicieron que Wizards of the Coast abandonara el sistema Elo para los torneos de Magic: the Gathering en favor de un sistema de su propia invención llamado "Puntos Planeswalker". ^{[40] [41]}

This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (January 2017) (Learn how and when to remove this message)

Un problema más sutil está relacionado con el emparejamiento. Cuando los jugadores pueden elegir a sus propios oponentes, pueden elegir oponentes con un riesgo mínimo de perder y una recompensa máxima por ganar. Algunos ejemplos particulares de jugadores con una puntuación de 2800+ que eligen oponentes con un riesgo mínimo y una posibilidad máxima de ganar puntuación incluyen: elegir oponentes que saben que pueden vencer con una determinada estrategia; elegir oponentes que creen que están sobrevalorados; o evitar jugar con jugadores fuertes que están varios cientos de puntos por debajo de ellos, pero que pueden tener títulos de ajedrez como MI o GM. En la categoría de elegir oponentes sobrevalorados, los nuevos participantes en el sistema de puntuación que han jugado menos de 50 partidas son en teoría un objetivo conveniente, ya que pueden estar sobrevalorados en su puntuación provisional. El ICC compensa este problema asignando un factor K más bajo al jugador establecido si gana contra un nuevo participante. El factor K es en realidad una función del número de partidas valoradas jugadas por el nuevo participante.

Por lo tanto, las clasificaciones Elo en línea siguen siendo un mecanismo útil para proporcionar una clasificación basada en la clasificación del oponente. Sin embargo, su credibilidad general debe verse en el contexto de al menos los dos problemas principales descritos anteriormente: abuso del motor y emparejamiento selectivo de oponentes.

El ICC también ha introducido recientemente clasificaciones de "emparejamiento automático", que se basan en emparejamientos aleatorios, pero en los que cada victoria consecutiva asegura un oponente estadísticamente mucho más difícil que también ha ganado x partidas seguidas. Con la participación de cientos de jugadores potenciales, esto crea algunos de los desafíos de un gran evento suizo que se disputa ferozmente, con ganadores de rondas enfrentándose a ganadores de rondas. Este enfoque de emparejamiento ciertamente maximiza el riesgo de clasificación de los participantes con mayor clasificación, que pueden enfrentar una oposición muy dura de jugadores por debajo de 3000, por ejemplo. Esta es una clasificación separada en sí misma, y ​​se encuentra dentro de las categorías de clasificación de "1 minuto" y "5 minutos". Las clasificaciones máximas logradas por encima de 2500 son excepcionalmente raras.

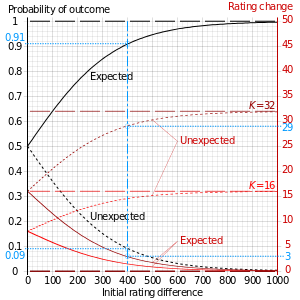
El término "inflación", aplicado a las clasificaciones, pretende sugerir que el nivel de fuerza de juego demostrado por el jugador clasificado está disminuyendo con el tiempo; por el contrario, "deflación" sugiere que el nivel está avanzando. Por ejemplo, si hay inflación, una clasificación moderna de 2500 significa menos que una clasificación histórica de 2500, mientras que lo contrario es cierto si hay deflación. El uso de clasificaciones para comparar jugadores entre diferentes épocas se hace más difícil cuando hay inflación o deflación. (Véase también Comparación de los mejores jugadores de ajedrez a lo largo de la historia .)

Al analizar las listas de clasificación de la FIDE a lo largo del tiempo, Jeff Sonas sugiere que la inflación puede haber tenido lugar desde aproximadamente 1985. ^[42] Sonas observa a los jugadores mejor clasificados, en lugar de a todos los jugadores clasificados, y reconoce que los cambios en la distribución de las clasificaciones podrían haber sido causados ​​por un aumento del nivel de juego en los niveles más altos, pero también busca otras causas.

El número de personas con puntuaciones superiores a 2700 ha aumentado. Alrededor de 1979 había solo un jugador en activo ( Anatoly Karpov ) con una puntuación tan alta. En 1992, Viswanathan Anand fue solo el octavo jugador en la historia del ajedrez en alcanzar la marca de 2700 en ese momento. ^[43] Esto aumentó a 15 jugadores en 1994. 33 jugadores tenían una puntuación de 2700+ en 2009 y 44 en septiembre de 2012. Solo 14 jugadores han roto alguna vez una puntuación de 2800.

Una posible causa de esta inflación fue el nivel mínimo de calificación, que durante mucho tiempo estuvo en 2200, y si un jugador caía por debajo de este nivel, era eliminado de la lista de calificación. Como consecuencia, los jugadores con un nivel de habilidad justo por debajo del mínimo solo estarían en la lista de calificación si estuvieran sobrevalorados, y esto haría que aportaran puntos al fondo de calificación. ^[42] En julio de 2000, la calificación promedio de los 100 mejores era de 2644. Para julio de 2012, había aumentado a 2703. ^[43]

Utilizando un potente motor de ajedrez para evaluar los movimientos realizados en partidas entre jugadores calificados, Regan y Haworth analizan conjuntos de partidas de torneos calificados por la FIDE y llegan a la conclusión de que hubo poca o ninguna inflación entre 1976 y 2009. ^[44]

En un sistema Elo puro, cada partida termina con una transacción igual de puntos de calificación. Si el ganador obtiene N puntos de calificación, el perdedor perderá N puntos de calificación. Esto evita que entren o salgan puntos del sistema cuando se juegan partidas y se califican. Sin embargo, los jugadores tienden a ingresar al sistema como novatos con una calificación baja y se retiran del sistema como jugadores experimentados con una calificación alta. Por lo tanto, a largo plazo, un sistema con transacciones estrictamente iguales tiende a resultar en una deflación de la calificación. ^[45]

En 1995, la USCF reconoció que varios jugadores jóvenes de nivel escolar estaban mejorando más rápido de lo que el sistema de clasificación podía registrar. Como resultado, los jugadores establecidos con clasificaciones estables comenzaron a perder puntos de clasificación en favor de los jugadores jóvenes y subestimados. Varios de los jugadores establecidos de mayor edad se sintieron frustrados por lo que consideraban una disminución injusta de la clasificación, y algunos incluso abandonaron el ajedrez por ello. ^[46]

Debido a la diferencia significativa en el momento en que se produce la inflación y la deflación, y para combatir la deflación, la mayoría de las implementaciones de las clasificaciones Elo tienen un mecanismo para inyectar puntos en el sistema con el fin de mantener las clasificaciones relativas a lo largo del tiempo. La FIDE tiene dos mecanismos inflacionarios. En primer lugar, las actuaciones por debajo de un "piso de clasificación" no se rastrean, por lo que un jugador con una verdadera habilidad por debajo del piso solo puede no ser calificado o estar sobrevalorado, nunca calificado correctamente. En segundo lugar, los jugadores establecidos y de mayor calificación tienen un factor K más bajo. Los nuevos jugadores tienen un K = 40 , que baja a K = 20 después de 30 partidas jugadas, y a K = 10 cuando el jugador llega a 2400. ^[31] El sistema actual en los Estados Unidos incluye un esquema de puntos de bonificación que alimenta puntos de clasificación en el sistema para rastrear a los jugadores que mejoran, y diferentes valores K para diferentes jugadores. ^[46] Algunos métodos, utilizados en Noruega por ejemplo, diferencian entre jugadores jóvenes y veteranos, y utilizan un factor K mayor para los jugadores jóvenes, aumentando incluso el progreso en la calificación en un 100% cuando obtienen una puntuación muy por encima de su rendimiento previsto. ^[47]

En Estados Unidos, los niveles mínimos de calificación funcionan garantizando que un jugador nunca caiga por debajo de un cierto límite. Esto también combate la deflación, pero el presidente del Comité de Calificaciones de la USCF ha criticado este método porque no otorga puntos adicionales a los jugadores que mejoran. Un posible motivo para estos niveles mínimos de calificación es combatir el sandbagging, es decir, la reducción deliberada de las calificaciones para poder optar a categorías y premios de menor calificación. ^[46]

Los encuentros de ajedrez entre humanos y computadoras entre 1997 ( Deep Blue versus Garry Kasparov ) y 2006 demostraron que las computadoras de ajedrez son capaces de derrotar incluso a los jugadores humanos más fuertes. Sin embargo, las calificaciones de los motores de ajedrez son difíciles de cuantificar, debido a factores variables como el control del tiempo y el hardware en el que se ejecuta el programa, y ​​también al hecho de que el ajedrez no es un juego limpio. La existencia y magnitud de la ventaja del primer movimiento en ajedrez se vuelve muy importante a nivel de computadora. Más allá de cierto umbral de habilidad, un motor con blancas debería ser capaz de forzar un empate a pedido desde la posición inicial incluso contra un juego perfecto, simplemente porque las blancas comienzan con una ventaja demasiado grande para perder en comparación con la pequeña magnitud de los errores que es probable que cometan. En consecuencia, un motor de este tipo tiene más o menos garantizado un puntaje de al menos el 25% incluso contra un juego perfecto. Las diferencias en la habilidad más allá de cierto punto solo se pueden detectar si uno no comienza desde la posición inicial habitual, sino que en su lugar elige una posición inicial que apenas está perdida para un bando. Debido a estos factores, las calificaciones dependen de los emparejamientos y las aperturas seleccionadas. ^[48] ​​Las listas de clasificación de motores publicadas, como CCRL, se basan en juegos con solo motor en configuraciones de hardware estándar y no son directamente comparables con las clasificaciones de la FIDE.

Para algunas estimaciones de calificaciones, consulte Motor de ajedrez § Calificaciones .

• Go : La Federación Europea de Go adoptó un sistema de clasificación basado en Elo, inicialmente iniciado por la Federación Checa de Go.
• Backgammon : El popular First Internet Backgammon Server (FIBS) calcula las clasificaciones basándose en un sistema Elo modificado. A los nuevos jugadores se les asigna una clasificación de 1500, y los mejores humanos y bots obtienen una clasificación superior a 2000. La misma fórmula ha sido adoptada por varios otros sitios de backgammon, como Play65 , DailyGammon, GoldToken y VogClub. VogClub establece la clasificación de un nuevo jugador en 1600. La Federación de Backgammon del Reino Unido utiliza la fórmula FIBS para sus clasificaciones nacionales del Reino Unido. ^[49]
• Scrabble : Las organizaciones nacionales de Scrabble calculan puntuaciones Elo distribuidas normalmente, excepto en el Reino Unido , donde se utiliza un sistema diferente. La Asociación de Jugadores de Scrabble de América del Norte tiene la población de miembros activos más grande, con aproximadamente 2000 a principios de 2011. Lexulous también utiliza el sistema Elo.
• A pesar de las dudas sobre la idoneidad de utilizar el sistema Elo para calificar juegos en los que la suerte es un factor, los fabricantes de juegos de cartas coleccionables suelen utilizar las clasificaciones Elo para sus esfuerzos de juego organizado. La DCI (anteriormente Duelists' Convocation International) utilizó las clasificaciones Elo para torneos de Magic: The Gathering y otros juegos de Wizards of the Coast . Sin embargo, la DCI abandonó este sistema en 2012 a favor de un nuevo sistema acumulativo de "Puntos Planeswalker", principalmente debido a la preocupación mencionada anteriormente de que Elo alienta a los jugadores con calificaciones altas a evitar jugar para "proteger su clasificación". ^{[40] [41]} Pokémon USA utiliza el sistema Elo para clasificar a sus competidores de juego organizado de TCG. ^[50] Los premios para los mejores jugadores en varias regiones incluían vacaciones e invitaciones a campeonatos mundiales hasta la temporada 2011-2012, donde los premios se basaban en un sistema de Puntos de Campeonato, siendo su lógica la misma que la de la DCI para Magic: The Gathering . De manera similar, Decipher, Inc. utilizó el sistema Elo para sus juegos clasificados como Star Trek Customizable Card Game y Star Wars Customizable Card Game .

El sistema de clasificación Elo se utiliza en la parte de ajedrez del boxeo ajedrecístico . Para poder participar en el boxeo ajedrecístico profesional, se debe tener una clasificación Elo de al menos 1600, además de competir en 50 o más combates de boxeo amateur o artes marciales.

El fútbol americano universitario utilizó el método Elo como parte de sus sistemas de clasificación de la Bowl Championship Series desde 1998 hasta 2013, después de lo cual el BCS fue reemplazado por el College Football Playoff . Jeff Sagarin de USA Today publica clasificaciones de equipos para la mayoría de los deportes estadounidenses, que incluyen clasificaciones del sistema Elo para el fútbol americano universitario. El uso de sistemas de clasificación fue efectivamente descartado con la creación del College Football Playoff en 2014.

En otros deportes, los individuos mantienen clasificaciones basadas en el algoritmo Elo. Estas suelen ser no oficiales, no avaladas por el organismo rector del deporte. Las clasificaciones Elo del fútbol mundial son un ejemplo del método aplicado al fútbol masculino . ^[51] En 2006, las clasificaciones Elo fueron adaptadas para los equipos de las Grandes Ligas de Béisbol por Nate Silver , entonces de Baseball Prospectus . ^[52] Con base en esta adaptación, ambos también hicieron simulaciones de Monte Carlo basadas en Elo de las probabilidades de que los equipos lleguen a los playoffs. ^[53] En 2014, Beyond the Box Score, un sitio de SB Nation , introdujo un sistema de clasificación Elo para el béisbol internacional. ^[54]

En tenis, el Universal Tennis Rating (UTR) basado en Elo clasifica a los jugadores a escala global, independientemente de la edad, el género o la nacionalidad. Es el sistema de clasificación oficial de las principales organizaciones como la Intercollegiate Tennis Association y World TeamTennis y se utiliza con frecuencia en segmentos del Tennis Channel . El algoritmo analiza más de 8 millones de resultados de partidos de más de 800.000 tenistas de todo el mundo. El 8 de mayo de 2018, Rafael Nadal , tras haber ganado 46 sets consecutivos en partidos en canchas de arcilla, tuvo un UTR en arcilla casi perfecto de 16,42. ^[55]

En el pool , se utiliza un sistema basado en Elo llamado Fargo Rate para clasificar a los jugadores en competiciones organizadas amateurs y profesionales. ^[56]

Una de las pocas clasificaciones basadas en Elo avaladas por el organismo rector de un deporte es la Clasificación Mundial Femenina de la FIFA , basada en una versión simplificada del algoritmo Elo, que la FIFA utiliza como su sistema de clasificación oficial para los equipos nacionales de fútbol femenino .

Desde la primera lista de clasificación después de la Copa Mundial de la FIFA 2018 , la FIFA ha utilizado Elo para su Clasificación Mundial de la FIFA . ^[57]

En 2015, Nate Silver, editor en jefe del sitio web de comentarios estadísticos FiveThirtyEight , y Reuben Fischer-Baum produjeron clasificaciones Elo para cada equipo y temporada de la Asociación Nacional de Baloncesto hasta la temporada 2014. ^{[58] [59]} En 2014, FiveThirtyEight creó clasificaciones basadas en Elo y proyecciones de victorias para la Liga Nacional de Fútbol Americano profesional . ^[60]

La Asociación Inglesa de Korfball clasificó a los equipos según las clasificaciones Elo, para determinar los handicaps para su competencia de copa para la temporada 2011/12.

Se ha desarrollado una clasificación basada en Elo de los jugadores de la Liga Nacional de Hockey . ^[61] La métrica de hockey-Elo evalúa el juego general de dos vías de un jugador: puntuación Y defensa tanto en situaciones de fuerza pareja como de juego de poder/penalti-kill.

Rugbyleagueratings.com utiliza el sistema de clasificación Elo para clasificar a los equipos de la liga de rugby internacional y de clubes .

Hemaratings.com se inició en 2017 y utiliza un algoritmo Glicko-2 para clasificar a los esgrimistas de artes marciales históricas europeas individuales en todo el mundo en diferentes categorías, como espada larga , estoque , sable histórico y espada y broquel . ^[62]

Muchos videojuegos utilizan sistemas Elo modificados en el juego competitivo. El juego MOBA League of Legends utilizó un sistema de clasificación Elo antes de la segunda temporada de juego competitivo. ^[63] El juego de deportes electrónicos Overwatch , la base de la organización deportiva profesional única Overwatch League , utiliza un derivado del sistema Elo para clasificar a los jugadores competitivos con varios ajustes realizados entre temporadas competitivas. ^[64] World of Warcraft también utilizó anteriormente el sistema Glicko-2 para formar equipos y comparar jugadores de Arena, pero ahora utiliza un sistema similar a TrueSkill de Microsoft . ^[65] El juego Puzzle Pirates utiliza el sistema de clasificación Elo para determinar las clasificaciones en los distintos rompecabezas. Este sistema también se utiliza en FIFA Mobile para los modos Division Rivals. Otro juego reciente que comenzó a utilizar el sistema de clasificación Elo es AirMech , que utiliza clasificaciones Elo ^[66] para emparejamientos aleatorios/en equipo 1v1, 2v2 y 3v3. RuneScape 3 utilizó el sistema Elo en el relanzamiento del minijuego del cazarrecompensas en 2016. ^[67] Mechwarrior Online instituyó un sistema Elo para su nuevo modo "Comp Queue", efectivo con el parche del 20 de junio de 2017. ^[68] Age of Empires II DE y Age of Empires III DE están utilizando el sistema Elo para su tabla de clasificación y emparejamiento, con nuevos jugadores comenzando en Elo 1000. ^[69] El Tetris clásico competitivo ( Tetris jugado en el Nintendo Entertainment System ) deriva sus calificaciones utilizando una combinación de las mejores puntuaciones personales de los jugadores y un sistema Elo altamente modificado. ^[70]

Pocos videojuegos utilizan el sistema de clasificación Elo original. Según Lichess , un servidor de ajedrez en línea, el sistema Elo está desactualizado, y muchas organizaciones de ajedrez ahora utilizan Glicko-2. ^[71] PlayerUnknown's Battlegrounds es uno de los pocos videojuegos que utiliza el primer sistema Elo. En Guild Wars , las clasificaciones Elo se utilizan para registrar la clasificación de gremio ganada y perdida a través de batallas de gremio contra gremio. En 1998, se lanzó una escalera de juegos en línea llamada Clanbase ^[72] , que usaba el sistema de puntuación Elo para clasificar a los equipos. El valor K inicial era 30, pero se cambió a 5 en enero de 2007, luego se cambió a 15 en julio de 2009. ^[73] El sitio luego se desconectó en 2013. ^[74] Un sitio alternativo similar se lanzó en 2016 con el nombre de Scrimbase , ^[75] que también usó el sistema de puntuación Elo para clasificar a los equipos. Desde 2005, Golden Tee Live clasifica a los jugadores según el sistema Elo. Los jugadores nuevos comienzan con 2100 puntos y los mejores tienen una puntuación superior a 3000. ^[76]

A pesar de que muchos videojuegos utilizan diferentes sistemas de emparejamiento , es común que los jugadores de videojuegos clasificados se refieran a todas las clasificaciones de emparejamiento como Elo .

El sistema de clasificación Elo se ha utilizado en biometría blanda ^[77] , que se ocupa de la identificación de individuos mediante descripciones humanas. Se utilizaron descripciones comparativas junto con el sistema de clasificación Elo para proporcionar "mediciones relativas" sólidas y discriminantes, que permitieran una identificación precisa.

El sistema de clasificación Elo también se ha utilizado en biología para evaluar las jerarquías de dominio masculino, ^[78] y en automatización y visión artificial para la inspección de tejidos . ^[79]

Además, los sitios de jueces en línea también utilizan el sistema de calificación Elo o sus derivados. Por ejemplo, Topcoder utiliza una versión modificada basada en la distribución normal, ^[80] mientras que Codeforces utiliza otra versión basada en la distribución logística. ^{[81] [82] [83]}

El sistema de calificación Elo también se ha observado en aplicaciones de citas, como en la aplicación de emparejamiento Tinder , que utiliza una variante del sistema de calificación Elo. ^[84]

El YouTuber Marques Brownlee y su equipo utilizaron el sistema de clasificación Elo cuando permitieron a las personas votar entre fotos digitales tomadas con diferentes modelos de teléfonos inteligentes lanzados en 2022. ^[85]

El sistema de clasificación Elo también se ha utilizado en los rankings de universidades con preferencia revelada en Estados Unidos , como los de la empresa de credenciales digitales Parchment. ^{[86] [87] [88]}

El sistema de clasificación Elo también se ha adoptado para evaluar los modelos de IA. En 2021, Anthropic utilizó el sistema Elo para clasificar los modelos de IA en su investigación. ^[89] La tabla de clasificación de LMSYS empleó brevemente el sistema de clasificación Elo para clasificar los modelos de IA ^[90] antes de realizar la transición al modelo Bradley-Terry . ^[91]

El sistema de clasificación Elo apareció de forma destacada en La red social durante la escena del algoritmo en la que Mark Zuckerberg lanzó Facemash . En la escena, Eduardo Saverin escribe fórmulas matemáticas para el sistema de clasificación Elo en la ventana del dormitorio de Zuckerberg. Tras bambalinas, según afirma la película, se utiliza el sistema Elo para clasificar a las chicas por su atractivo. Las ecuaciones que impulsan el algoritmo se muestran brevemente, escritas en la ventana; ^[92] sin embargo, son ligeramente incorrectas. ^{[ cita requerida ]}

• Elo infierno
• Índice de porcentaje de calificación (RPI), otro sistema que incorpora la fuerza de los oponentes

• Elo, Arpad (1986) [1.ª edición, 1978]. La clasificación de los jugadores de ajedrez, pasados ​​y presentes (segunda edición). Nueva York: Arco Publishing, Inc. ISBN 978-0-668-04721-0.

• Harkness, Kenneth (1967). Manual oficial de ajedrez . McKay.

• Página de investigación de Mark Glickman, con varios enlaces a artículos técnicos sobre sistemas de clasificación de ajedrez