Geodesia

Ciencia que mide la forma, orientación y gravedad de la Tierra.

La geodesia o geodésica ^[1] es la ciencia de medir y representar la geometría , la gravedad y la orientación espacial de la Tierra en 3D que varía temporalmente . Se denomina geodesia planetaria cuando se estudian otros cuerpos astronómicos , como los planetas o los sistemas circumplanetarios . ^[2] La geodesia es una ciencia de la Tierra y muchos consideran que el estudio de la forma y la gravedad de la Tierra es fundamental para esa ciencia. ^[3]^[4] También es una disciplina de las matemáticas aplicadas . ^[5]^[6]

Los fenómenos geodinámicos , incluidos el movimiento de la corteza , las mareas y el movimiento polar , se pueden estudiar mediante el diseño de redes de control globales y nacionales , la aplicación de técnicas de geodesia espacial y geodésica terrestre y el uso de datos y sistemas de coordenadas . Los puestos de trabajo en geodesia incluyen geodesista y topógrafo geodésico . ^[7]

Historia

La geodesia comenzó en la antigüedad precientífica , por lo que la palabra geodesia proviene del griego antiguo γεωδαισία o geodaisia (literalmente, "división de la Tierra").

Las primeras ideas sobre la figura de la Tierra sostenían que la Tierra era plana y que los cielos eran una cúpula física que se extendía sobre ella. ^{[ cita requerida ]} Dos de los primeros argumentos a favor de una Tierra esférica eran que los eclipses lunares aparecen ante un observador como sombras circulares y que Polaris aparece cada vez más baja en el cielo para un viajero que se dirige al sur.

Definición

En inglés , la geodesia se refiere a la ciencia de medir y representar información geoespacial , mientras que la geomática abarca aplicaciones prácticas de la geodesia a escala local y regional, incluida la topografía .

En alemán , geodesia puede referirse a la geodesia superior ( höhere Geodäsie o Erdmessung , literalmente "geomensuración"), que se ocupa de medir la Tierra a escala global, o a la geodesia de ingeniería ( Ingenieurgeodäsie ), que incluye la topografía, es decir, la medición de partes o regiones de la Tierra.

Durante mucho tiempo, la geodesia fue la ciencia de medir y comprender la forma geométrica de la Tierra, su orientación en el espacio y el campo gravitacional; sin embargo, la ciencia y las operaciones geodésicas también se aplican a otros cuerpos astronómicos de nuestro Sistema Solar . ^[2]

En gran medida, la forma de la Tierra es el resultado de la rotación , que provoca su abultamiento ecuatorial , y de la competencia de procesos geológicos como la colisión de placas , así como del vulcanismo , a los que se opone el campo gravitatorio terrestre. Esto se aplica a la superficie sólida, a la superficie líquida ( topografía dinámica de la superficie del mar ) y a la atmósfera terrestre . Por esta razón, el estudio del campo gravitatorio terrestre se denomina geodesia física .

Geoide y elipsoide de referencia

El geoide es esencialmente la figura de la Tierra abstraída de sus características topográficas . Es una superficie de equilibrio idealizada del agua de mar , la superficie del nivel medio del mar en ausencia de corrientes y variaciones de presión del aire , y continua bajo las masas continentales. A diferencia de un elipsoide de referencia , el geoide es irregular y demasiado complicado para servir como superficie computacional para resolver problemas geométricos como el posicionamiento de puntos. La separación geométrica entre el geoide y un elipsoide de referencia se llama ondulación geoidal y varía globalmente entre ±110 m según el elipsoide GRS 80.

Un elipsoide de referencia, elegido habitualmente para que tenga el mismo tamaño (volumen) que el geoide, se describe por su semieje mayor (radio ecuatorial) a y su aplanamiento f . La cantidad f = ⁠a - b/a⁠ , donde b es el semieje menor (radio polar), es puramente geométrica. La elipticidad mecánica de la Tierra (aplanamiento dinámico, símbolo J ₂ ) se puede determinar con alta precisión mediante la observación de perturbaciones de la órbita de los satélites . Su relación con el aplanamiento geométrico es indirecta y depende de la distribución de densidad interna o, en términos más simples, del grado de concentración central de masa.

El Sistema de Referencia Geodésica de 1980 ( GRS 80 ), adoptado en la XVII Asamblea General de la Unión Internacional de Geodesia y Geofísica ( IUGG ), postuló un semieje mayor de 6.378.137 m y un aplanamiento de 1:298,257. El GRS 80 constituye esencialmente la base para el posicionamiento geodésico mediante el Sistema de Posicionamiento Global (GPS) y, por lo tanto, también se utiliza ampliamente fuera de la comunidad geodésica. Numerosos sistemas utilizados para la cartografía y la cartografía se están volviendo obsoletos a medida que los países se mueven cada vez más hacia sistemas de referencia geocéntricos globales que utilizan el elipsoide de referencia GRS 80.

El geoide es una superficie "realizable", lo que significa que puede ubicarse de manera consistente en la Tierra mediante mediciones simples adecuadas a partir de objetos físicos como un mareógrafo . Por lo tanto, el geoide puede considerarse una superficie física ("real"). Sin embargo, el elipsoide de referencia tiene muchas instancias posibles y no es fácilmente realizable, por lo que es una superficie abstracta. La tercera superficie principal de interés geodésico, la superficie topográfica de la Tierra, también es realizable.

Sistemas de coordenadas en el espacio

Las ubicaciones de los puntos en el espacio 3D se describen de manera más conveniente mediante tres coordenadas cartesianas o rectangulares, X , Y y Z. Desde la llegada del posicionamiento por satélite, dichos sistemas de coordenadas suelen ser geocéntricos , con el eje Z alineado con el eje de rotación de la Tierra (convencional o instantáneo).

Antes de la era de la geodesia satelital , los sistemas de coordenadas asociados con un datum geodésico intentaban ser geocéntricos , pero con un origen que difería del geocentro en cientos de metros debido a desviaciones regionales en la dirección de la plomada (vertical). Estos datums geodésicos regionales, como ED 50 (Datum europeo 1950) o NAD 27 (Datum norteamericano 1927), tienen elipsoides asociados que son los "mejores ajustes" regionales a los geoides dentro de sus áreas de validez, lo que minimiza las desviaciones de la vertical sobre estas áreas.

Es sólo porque los satélites GPS orbitan alrededor del geocentro que este punto se convierte naturalmente en el origen de un sistema de coordenadas definido por medios geodésicos satelitales, ya que las posiciones de los satélites en el espacio se calculan dentro de dicho sistema.

Los sistemas de coordenadas geocéntricas utilizados en geodesia se pueden dividir naturalmente en dos clases:

Los sistemas de referencia inerciales , donde los ejes de coordenadas mantienen su orientación con respecto a las estrellas fijas o, equivalentemente, a los ejes de rotación de los giroscopios ideales . El eje X apunta al equinoccio de primavera .
Los sistemas de referencia corrotativos (también denominados ECEF o "Earth Centered, Earth Fixed"), en los que los ejes están "fijados" al cuerpo sólido de la Tierra. El eje X se encuentra dentro del plano meridiano del observatorio de Greenwich .

La transformación de coordenadas entre estos dos sistemas hasta una buena aproximación se describe mediante el tiempo sideral (aparente) , que tiene en cuenta las variaciones en la rotación axial de la Tierra ( variaciones en la duración del día ). Una descripción más precisa también tiene en cuenta el movimiento polar como un fenómeno que los geodestas siguen de cerca.

Sistemas de coordenadas en el plano

En aplicaciones geodésicas como topografía y cartografía , se utilizan dos tipos generales de sistemas de coordenadas en el plano:

Plano-polar , con puntos en el plano definidos por su distancia, s , desde un punto específico a lo largo de un rayo que tiene una dirección α desde una línea base o eje.
Rectangular , con puntos definidos por distancias desde dos ejes mutuamente perpendiculares, x e y . Contrariamente a la convención matemática, en la práctica geodésica, el eje x apunta al norte y el eje y al este .

Se pueden utilizar de forma intuitiva coordenadas rectangulares en el plano para la ubicación actual, en cuyo caso el eje x apuntará al norte local. De manera más formal, dichas coordenadas se pueden obtener a partir de coordenadas 3D utilizando el artificio de una proyección cartográfica . Es imposible representar la superficie curva de la Tierra en una superficie cartográfica plana sin deformarla. El compromiso elegido con más frecuencia, denominado proyección conforme , conserva los ángulos y las proporciones de longitud de modo que los círculos pequeños se representan como círculos pequeños y los cuadrados pequeños como cuadrados.

Un ejemplo de este tipo de proyección es la UTM ( Universal Transverse Mercator ). Dentro del plano cartográfico, tenemos las coordenadas rectangulares x e y . En este caso, la dirección norte que se utiliza como referencia es el norte del mapa , no el norte local . La diferencia entre ambos se denomina convergencia de meridianos .

Es bastante fácil "traducir" entre coordenadas polares y rectangulares en el plano: sea, como arriba, la dirección y la distancia α y s respectivamente, entonces tenemos

{\begin{aligned}x&=s\cos \alpha \\y&=s\sin \alpha \end{aligned}}

La transformación inversa viene dada por:

{\begin{aligned}s&={\sqrt {x^{2}+y^{2}}}\\\alpha &=\arctan {\frac {y}{x}}.\end{aligned}}

Alturas

Medición de altura mediante altimetría satelital

En geodesia, las alturas de puntos o terrenos se miden " por encima del nivel del mar " como una superficie irregular y definida físicamente. Los sistemas de altura que se utilizan son:

Cada sistema tiene sus ventajas y desventajas. Tanto las alturas ortométricas como las normales se expresan en metros sobre el nivel del mar, mientras que los números geopotenciales son medidas de energía potencial (unidad: m ² s ⁻² ) y no métricas. La superficie de referencia es el geoide , una superficie equigeopotencial que se aproxima al nivel medio del mar como se describió anteriormente. Para las alturas normales, la superficie de referencia es el llamado cuasigeoide , que tiene una separación de unos pocos metros del geoide debido al supuesto de densidad en su continuación bajo las masas continentales. ^[8]

Estas alturas se pueden relacionar a través del concepto de ondulación geoidal con las alturas elipsoidales (también conocidas como alturas geodésicas ), que representan la altura de un punto por encima del elipsoide de referencia . Los receptores de posicionamiento por satélite suelen proporcionar alturas elipsoidales a menos que estén equipados con un software de conversión especial basado en un modelo del geoide.

Datums geodésicos

Como las coordenadas y alturas de los puntos geodésicos siempre se obtienen dentro de un sistema que se construyó a partir de observaciones del mundo real, los geodesistas introdujeron el concepto de "datum geodésico" (en plural, datums ): una realización física (del mundo real) de un sistema de coordenadas utilizado para describir la ubicación de puntos. Esta realización se deriva de la elección de valores de coordenadas (por lo tanto convencionales) para uno o más puntos de referencia. En el caso de los datos de altura, basta con elegir un punto de referencia: el punto de referencia, normalmente un mareómetro en la costa. Así, tenemos datums verticales, como el NAVD 88 (North American Vertical Datum 1988), el NAP ( Normaal Amsterdams Peil ), el datum de Kronstadt, el datum de Trieste y muchos otros.

Tanto en matemáticas como en geodesia, un sistema de coordenadas es un "sistema de coordenadas" según la terminología ISO , mientras que el Servicio Internacional de Sistemas de Referencia y Rotación de la Tierra (IERS) utiliza el término "sistema de referencia" para lo mismo. Cuando las coordenadas se obtienen eligiendo puntos de referencia y fijando un datum geodésico, la ISO habla de un "sistema de referencia de coordenadas", mientras que el IERS utiliza un "marco de referencia" para lo mismo. El término ISO para una transformación de datum es nuevamente una "transformación de coordenadas". ^[9]

Posicionamiento

El geoposicionamiento general , o simplemente posicionamiento, es la determinación de la ubicación de puntos en la Tierra, mediante una miríada de técnicas. El posicionamiento geodésico emplea métodos geodésicos para determinar un conjunto de coordenadas geodésicas precisas de un punto en la tierra, en el mar o en el espacio. Puede realizarse dentro de un sistema de coordenadas ( posicionamiento de puntos o posicionamiento absoluto ) o en relación con otro punto ( posicionamiento relativo ). Se calcula la posición de un punto en el espacio a partir de mediciones que vinculan puntos terrestres o extraterrestres de ubicación conocida ("puntos conocidos") con puntos terrestres de ubicación desconocida ("puntos desconocidos"). El cálculo puede implicar transformaciones entre sistemas de coordenadas astronómicos y terrestres. Los puntos conocidos utilizados en el posicionamiento de puntos pueden ser estaciones de referencia GNSS de funcionamiento continuo o puntos de triangulación de una red de orden superior.

Tradicionalmente, los geodestas construían una jerarquía de redes para permitir la localización de puntos dentro de un país. Las más altas en esta jerarquía eran las redes de triangulación, densificadas en redes de polígonos a los que se vinculaban las mediciones de mapeo y topografía locales, generalmente obtenidas utilizando una cinta métrica, un prisma de esquina y los postes rojos y blancos.

En la actualidad, el sistema GPS es el más utilizado, excepto para mediciones especializadas (por ejemplo, en ingeniería subterránea o de alta precisión). Las redes de orden superior se miden con GPS estático , utilizando la medición diferencial para determinar vectores entre puntos terrestres. Estos vectores se ajustan luego de forma tradicional. Un poliedro global de estaciones GPS en funcionamiento permanente bajo los auspicios del IERS es la base para definir un único marco de referencia geocéntrico global que sirve como referencia de "orden cero" (global) a la que se adjuntan las mediciones nacionales.

El posicionamiento cinemático en tiempo real (RTK GPS) se utiliza con frecuencia en la cartografía topográfica . En esa técnica de medición, los puntos desconocidos se pueden vincular rápidamente con puntos terrestres conocidos cercanos.

Uno de los objetivos del posicionamiento de puntos es proporcionar puntos conocidos para realizar mediciones cartográficas, también conocidas como control (horizontal y vertical). Puede haber miles de esos puntos determinados geodésicamente en un país, generalmente documentados por agencias cartográficas nacionales. Los topógrafos que trabajan en el sector inmobiliario y de seguros los utilizan para vincular sus mediciones locales.

Problemas geodésicos

En geodesia geométrica hay dos problemas principales:

Primer problema geodésico (también conocido como problema geodésico directo o hacia adelante ): dadas las coordenadas de un punto y la dirección ( azimut ) y la distancia a un segundo punto, determinar las coordenadas de ese segundo punto.
Segundo problema geodésico (también conocido como problema geodésico inverso o reverso ): dadas las coordenadas de dos puntos, determinar el acimut y la longitud de la línea (recta, curva o geodésica ) que conecta esos puntos.

Las soluciones de ambos problemas en geometría plana se reducen a trigonometría simple y son válidas para áreas pequeñas en la superficie de la Tierra; en una esfera, las soluciones se vuelven significativamente más complejas ya que, por ejemplo, en el problema inverso, los acimutes difieren al ir entre los dos puntos finales a lo largo del arco del círculo máximo que los conecta .

La solución general se denomina geodésica para la superficie considerada y las ecuaciones diferenciales para la geodésica se pueden resolver numéricamente. En el elipsoide de revolución, las geodésicas se pueden expresar en términos de integrales elípticas, que generalmente se evalúan en términos de una expansión en serie; véanse, por ejemplo, las fórmulas de Vincenty .

Conceptos de observación

Inclinación axial (u oblicuidad ), eje de rotación, plano de órbita , ecuador celeste y eclíptica . La Tierra se muestra tal como se ve desde el Sol ; la dirección de la órbita es en sentido contrario a las agujas del reloj (hacia la izquierda).

Tal como se define en geodesia (y también en astronomía ), algunos conceptos de observación básicos como ángulos y coordenadas incluyen (más comúnmente desde el punto de vista de un observador local):

Plomada o vertical : (la línea a lo largo de) la dirección de la gravedad local.
Cenit : la (dirección hacia la) intersección del vector de gravedad que se extiende hacia arriba en un punto y la esfera celeste .
Nadir : el punto antípoda (dirección hacia el) donde el vector de gravedad que se extiende hacia abajo interseca la esfera celeste (oculta).
Horizonte celeste : plano perpendicular al vector de gravedad en un punto.
Acimut : ángulo de dirección dentro del plano del horizonte, normalmente contado en el sentido de las agujas del reloj desde el norte (en geodesia y astronomía) o el sur (en Francia).
Elevación : la altura angular de un objeto sobre el horizonte; alternativamente: distancia cenital igual a 90 grados menos la elevación.
Coordenadas topocéntricas locales : acimut (ángulo de dirección dentro del plano del horizonte), ángulo de elevación (o ángulo cenital), distancia.
Polo norte celeste : extensión del eje de rotación instantánea de la Tierra ( en precesión y nutación ) que se extiende hacia el norte para intersecar la esfera celeste. (Lo mismo ocurre con el polo sur celeste).
Ecuador celeste : la intersección (instantánea) del plano ecuatorial de la Tierra con la esfera celeste.
Plano meridiano : cualquier plano perpendicular al ecuador celeste y que contiene los polos celestes.
Meridiano local : plano que contiene la dirección hacia el cenit y el polo celeste.

Medidas

La superficie de referencia (nivel) utilizada para determinar las diferencias de altura y los sistemas de referencia de altura se conoce como nivel medio del mar . El nivel de burbuja tradicional produce directamente dichas alturas (más útiles para fines prácticos) sobre el nivel del mar ; el uso más económico de los instrumentos GPS para la determinación de la altura requiere un conocimiento preciso de la figura del geoide , ya que el GPS solo proporciona alturas por encima del elipsoide de referencia GRS80 . A medida que mejora la determinación del geoide, se puede esperar que también aumente el uso del GPS en la determinación de la altura.

El teodolito es un instrumento que se utiliza para medir ángulos horizontales y verticales (en relación con la vertical local) respecto de puntos de referencia. Además, el taquímetro determina, electrónicamente o electroópticamente , la distancia a un objetivo y su funcionamiento es altamente automatizado o incluso robótico. Muy utilizado para el mismo fin es el método de posición de estación libre.

Generalmente, para los estudios de detalle locales se emplean taquímetros, aunque la antigua técnica rectangular que utiliza un prisma angular y una cinta de acero sigue siendo una alternativa económica. Como se mencionó, también existen técnicas GPS cinemáticas en tiempo real (RTK) rápidas y relativamente precisas. Los datos recopilados se etiquetan y registran digitalmente para su ingreso en bases de datos de sistemas de información geográfica (SIG).

Los receptores GNSS geodésicos (más comúnmente GPS ) generan directamente coordenadas 3D en un marco de coordenadas geocéntricas . Uno de estos marcos es el WGS84 , así como los marcos del Servicio Internacional de Sistemas de Referencia y Rotación de la Tierra ( IERS ). Los receptores GNSS han reemplazado casi por completo a los instrumentos terrestres para los estudios de redes de base a gran escala.

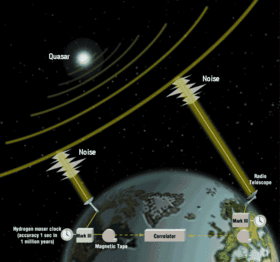
Para monitorear las irregularidades de rotación de la Tierra y los movimientos tectónicos de las placas y para realizar estudios geodésicos a nivel planetario, se emplean métodos de interferometría de línea de base muy larga (VLBI) que mide distancias a cuásares , medición láser lunar (LLR) que mide distancias a prismas en la Luna, y medición láser satelital (SLR) que mide distancias a prismas en satélites artificiales .

La gravedad se mide utilizando gravímetros , de los cuales hay dos tipos. En primer lugar están los gravímetros absolutos , basados en la medición de la aceleración de la caída libre (por ejemplo, de un prisma reflector en un tubo de vacío ). Se utilizan para establecer un control geoespacial vertical o en el campo. En segundo lugar, los gravímetros relativos están basados en resortes y son más comunes. Se utilizan en estudios de gravedad sobre grandes áreas, para establecer la figura del geoide sobre estas áreas. Los gravímetros relativos más precisos se denominan gravímetros superconductores , que son sensibles a una milésima de una milmillonésima de la gravedad de la superficie de la Tierra. Se utilizan unos veinte gravímetros superconductores en todo el mundo para estudiar las mareas , la rotación , la carga interior, oceánica y atmosférica de la Tierra, así como para verificar la constante de gravitación newtoniana .

En el futuro, la gravedad y la altitud podrían llegar a ser mensurables utilizando el concepto relativista especial de dilatación del tiempo medido por relojes ópticos .

Unidades y medidas en el elipsoide

La latitud y longitud geográficas se expresan en unidades de grados, minutos de arco y segundos de arco. Son ángulos , no medidas métricas, y describen la dirección de la normal local al elipsoide de revolución de referencia. Esta dirección es aproximadamente la misma que la dirección de la plomada, es decir, la gravedad local, que también es la normal a la superficie del geoide. Por esta razón, la determinación de la posición astronómica (medir la dirección de la plomada por medios astronómicos) funciona razonablemente bien cuando también se utiliza un modelo elipsoidal de la figura de la Tierra.

Una milla geográfica, definida como un minuto de arco sobre el ecuador, equivale a 1.855,32571922 m. Una milla náutica es un minuto de latitud astronómica. El radio de curvatura del elipsoide varía con la latitud, siendo el más largo en el polo y el más corto en el ecuador, al igual que ocurre con la milla náutica.

El metro se definió originalmente como la 10 millonésima parte de la longitud desde el ecuador hasta el polo norte a lo largo del meridiano que pasa por París (el objetivo no se alcanzó del todo en la implementación real, ya que está desfasado en 200 ppm en las definiciones actuales). Esta situación significa que un kilómetro equivale aproximadamente a (1/40.000) * 360 * 60 minutos de arco meridionales, o 0,54 millas náuticas. (Esto no es exactamente así, ya que las dos unidades se habían definido sobre bases diferentes, por lo que la milla náutica internacional es exactamente 1.852 m, lo que corresponde a redondear el cociente de 1.000/0,54 m a cuatro dígitos).

Cambios temporales

En geodesia se utilizan diversas técnicas para estudiar superficies, cuerpos de masa, campos físicos y sistemas dinámicos que cambian en el tiempo. Los puntos de la superficie terrestre cambian de ubicación debido a diversos mecanismos:

Movimiento de placas continentales, tectónica de placas ^[10]
El movimiento episódico de origen tectónico, especialmente cerca de las líneas de falla.
Efectos periódicos debidos a las mareas y la carga de marea ^[11]
Elevación del terreno postglacial debido al ajuste isostático
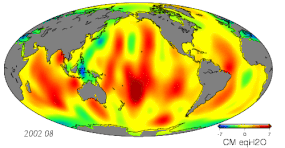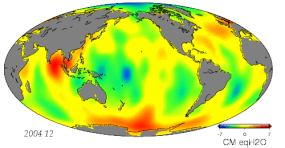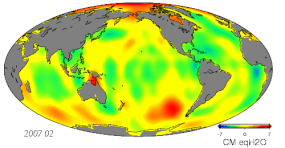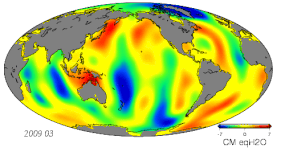
Variaciones de masa debidas a cambios hidrológicos, incluida la atmósfera, la criosfera, la hidrología terrestre y los océanos.
Movimiento polar subdiario ^[12]
Variabilidad de la duración del día ^[13]
Variaciones del centro de masas (geocentro) de la Tierra ^[14]
Movimientos antropogénicos como la construcción de embalses o la extracción de petróleo o agua.

Un gerente de proyecto de la NASA habla sobre su trabajo para el Proyecto de Geodesia Espacial , incluida una descripción general de sus cuatro técnicas fundamentales: GPS, VLBI , LLR / SLR y DORIS .

La geodinámica es la disciplina que estudia las deformaciones y movimientos de la corteza terrestre y su solidez en su conjunto. A menudo, el estudio de la rotación irregular de la Tierra se incluye en la definición anterior. Los estudios geodinámicos requieren marcos de referencia terrestres ^[15] realizados por las estaciones pertenecientes al Sistema de Observación Geodésica Global (GGOS ^[16] ).

Las técnicas para estudiar los fenómenos geodinámicos a escala global incluyen:

Posicionamiento satelital por GPS , GLONASS , Galileo y BeiDou
Interferometría de línea de base muy larga (VLBI)
Medición de distancia por láser satelital (SLR) ^[17] y medición de distancia por láser lunar (LLR)
Doris
Nivelación precisa a nivel regional y local
Taquímetros precisos
Monitoreo del cambio de gravedad mediante gravimetría terrestre, aérea, marítima y espacial
Altimetría satelital basada en observaciones de microondas y láser para estudiar la superficie del océano, el aumento del nivel del mar y el monitoreo de la capa de hielo.
Radar de apertura sintética interferométrica (InSAR) que utiliza imágenes de satélite.

Geodesistas notables

Véase también

Ciencia del sistema terrestre : estudio científico de las esferas de la Tierra y sus sistemas naturales integrados.
Lista de geodesistas – Geodesistas notables
Ingeniería geomática – Disciplina de datos geográficosPages displaying short descriptions of redirect targets
Historia de la geofísica
Geodinámica – Estudio de la dinámica de la Tierra.
Ciencia planetaria – Ciencia de los planetas y sistemas planetarios

Referencias

^ "geodésica". Diccionario Cambridge inglés . Consultado el 8 de junio de 2024 .
^ ab Vaníček, Petr ; Krakiwsky, Edward J., eds. (1 de noviembre de 1986). "Estructura de la Geodesia". Geodesia: los conceptos (Segunda ed.). Elsevier . págs. 45–51. doi :10.1016/B978-0-444-87775-8.50009-5. ISBN 978-0-444-87775-8... se pensaba que la geodesia ocupaba el espacio delimitado por la siguiente definición... " la ciencia de medir y representar la superficie de la Tierra". ... la nueva definición de geodesia... "la disciplina que trata de la medición y representación de la Tierra, incluido su campo gravitacional, en un espacio tridimensional variable en el tiempo". ... una definición prácticamente idéntica... la inclusión de otros cuerpos celestes y sus respectivos campos gravitacionales.
^ ¿ Qué es la geodesia? (PDF) . Asociación Internacional de Geodesia .
^ Departamento de Comercio de los Estados Unidos, Administración Nacional Oceánica y Atmosférica. "¿Qué es la geodesia?". oceanservice.noaa.gov . Consultado el 9 de junio de 2024 .
^ "Geodesia". Centro de Geoinformática de la Universidad Estatal de Luisiana . Consultado el 8 de junio de 2024 .
^ "Definición, características y ramas de la geodesia". Study.com . Consultado el 8 de junio de 2024. La definición de geodesia se puede explicar como el campo académico de las ciencias de la Tierra que se ocupa de medir y comprender la orientación de la Tierra en el espacio, el campo gravitacional de la Tierra y la forma geométrica de la Tierra. ... La geodesia es una disciplina matemática aplicada que se utiliza para comprender varios aspectos de la Tierra.
^ "Topógrafos geodésicos". Red de información ocupacional . 26 de noviembre de 2020. Consultado el 28 de enero de 2022 .
^ Foroughi, Ismael; Tenzer, Robert (2017). "Comparación de diferentes métodos para estimar la separación entre geoide y cuasi-geoide". Revista Geofísica Internacional . 210 (2): 1001–1020. doi : 10.1093/gji/ggx221 . hdl : 10397/75053 . ISSN 0956-540X.
^ (ISO 19111: Referenciación espacial por coordenadas).
^ Altamimi, Zuheir; Métivier, Laurent; Rebischung, Paul; Rouby, Hélène; Collilieux, Xavier (junio de 2017). "Modelo de movimiento de placa ITRF2014". Revista Geofísica Internacional . 209 (3): 1906-1912. doi : 10.1093/gji/ggx136 .
^ Sośnica, Krzysztof; Thaller, Daniela; Dach, Rolf; Jäggi, Adrian; Beutler, Gerhard (agosto de 2013). "Impacto de los desplazamientos de carga en los parámetros derivados del SLR y en la consistencia entre los resultados GNSS y SLR" (PDF) . Journal of Geodesy . 87 (8): 751–769. Bibcode :2013JGeod..87..751S. doi :10.1007/s00190-013-0644-1. S2CID 56017067. Archivado (PDF) desde el original el 2022-03-18.
^ Zajdel, Radosław; Sośnica, Krzysztof; Enterrar, Grzegorz; Dach, Rolf; Prange, Lars; Kazmierski, Kamil (enero de 2021). "Movimiento polar subdiario de GPS, GLONASS y Galileo". Revista de Geodesia . 95 (1): 3. Bibcode : 2021JGeod..95....3Z. doi : 10.1007/s00190-020-01453-w .
^ Zajdel, Radosław; Sośnica, Krzysztof; Enterrar, Grzegorz; Dach, Rolf; Prange, Lars (julio de 2020). "Errores sistemáticos específicos del sistema en los parámetros de rotación de la Tierra derivados de GPS, GLONASS y Galileo". Soluciones GPS . 24 (3): 74. Código Bib : 2020GPSS...24...74Z. doi : 10.1007/s10291-020-00989-w .
^ Zajdel, Radosław; Sośnica, Krzysztof; Bury, Grzegorz (enero de 2021). "Coordenadas del geocentro derivadas de multi-GNSS: una mirada al papel del modelado de la presión de la radiación solar". GPS Solutions . 25 (1): 1. Bibcode :2021GPSS...25....1Z. doi : 10.1007/s10291-020-01037-3 .
^ Zajdel, R.; Sośnica, K.; Drożdżewski, M.; Bury, G.; Strugarek, D. (noviembre de 2019). "Impacto de la restricción de red en la realización del marco de referencia terrestre basado en observaciones SLR para LAGEOS". Journal of Geodesy . 93 (11): 2293–2313. Bibcode :2019JGeod..93.2293Z. doi : 10.1007/s00190-019-01307-0 .
^ Sośnica, Krzysztof; Bosy, Jarosław (2019). "Sistema mundial de observación geodésica 2015-2018". Geodesia y Cartografía . doi : 10.24425/gac.2019.126090 .
^ Pearlman, M.; Arnold, D.; Davis, M.; Barlier, F.; Biancale, R.; Vasiliev, V.; Ciufolini, I.; Paolozzi, A.; Pavlis, EC; Sośnica, K.; Bloßfeld, M. (noviembre de 2019). "Satélites geodésicos láser: una herramienta científica de alta precisión". Revista de Geodesia . 93 (11): 2181–2194. Código Bibliográfico :2019JGeod..93.2181P. doi :10.1007/s00190-019-01228-y. S2CID 127408940.

Lectura adicional

FR Helmert, Teorías matemáticas y físicas de la geodesia superior, Parte 1, ACIC (St. Louis, 1964). Esta es una traducción al inglés de Die mathematischen und physikalischen Theorieen der höheren Geodäsie , Vol 1 (Teubner, Leipzig, 1880).
FR Helmert, Teorías matemáticas y físicas de la geodesia superior, Parte 2, ACIC (St. Louis, 1964). Esta es una traducción al inglés de Die mathematischen und physikalischen Theorieen der höheren Geodäsie , Vol 2 (Teubner, Leipzig, 1884).
B. Hofmann-Wellenhof y H. Moritz, Physical Geodesy , Springer-Verlag Wien, 2005. (Este texto es una edición actualizada del clásico de 1967 de WA Heiskanen y H. Moritz).
W. Kaula, Teoría de la geodesia satelital: aplicaciones de los satélites a la geodesia , Dover Publications, 2000. (Este texto es una reimpresión del clásico de 1966).
Vaníček P. y EJ Krakiwsky, Geodesia: los conceptos , págs. 714, Elsevier, 1986.
Torge, W (2001), Geodesia (3.ª edición), publicado por de Gruyter, ISBN 3-11-017072-8 .
Thomas H. Meyer, Daniel R. Roman y David B. Zilkoski. "¿Qué significa realmente la altura ?" (Esta es una serie de cuatro artículos publicados en Surveying and Land Information Science, SaLIS ).
- "Parte I: Introducción" SaLIS Vol. 64, No. 4, páginas 223–233, diciembre de 2004.
- "Parte II: Física y gravedad" SaLIS Vol. 65, No. 1, páginas 5–15, marzo de 2005.
- "Parte III: Sistemas de altura" SaLIS Vol. 66, No. 2, páginas 149–160, junio de 2006.
- "Parte IV: Detección de altura mediante GPS" SaLIS Vol. 66, No. 3, páginas 165–183, septiembre de 2006.

Enlaces externos

Geodesia en Wikilibros Medios relacionados con Geodesia en Wikimedia Commons

Nota de orientación sobre conciencia geodésica, Subcomité de Geodesia, Comité de Geomática, Asociación Internacional de Productores de Petróleo y Gas
"Geodesia" . Encyclopædia Britannica . Vol. 11 (11.ª ed.). 1911. págs. 607–615.

[1] "geodésica". Diccionario Cambridge inglés . Consultado el 8 de junio de 2024 .

[VK-2] Vaníček, Petr ; Krakiwsky, Edward J., eds. (1 de noviembre de 1986). "Estructura de la Geodesia". Geodesia: los conceptos (Segunda ed.). Elsevier . págs. 45–51. doi :10.1016/B978-0-444-87775-8.50009-5. ISBN 978-0-444-87775-8... se pensaba que la geodesia ocupaba el espacio delimitado por la siguiente definición... " la ciencia de medir y representar la superficie de la Tierra". ... la nueva definición de geodesia... "la disciplina que trata de la medición y representación de la Tierra, incluido su campo gravitacional, en un espacio tridimensional variable en el tiempo". ... una definición prácticamente idéntica... la inclusión de otros cuerpos celestes y sus respectivos campos gravitacionales.

[3] ^ ¿ Qué es la geodesia? (PDF) . Asociación Internacional de Geodesia .

[4] Departamento de Comercio de los Estados Unidos, Administración Nacional Oceánica y Atmosférica. "¿Qué es la geodesia?". oceanservice.noaa.gov . Consultado el 9 de junio de 2024 .

[5] "Geodesia". Centro de Geoinformática de la Universidad Estatal de Luisiana . Consultado el 8 de junio de 2024 .

[6] "Definición, características y ramas de la geodesia". Study.com . Consultado el 8 de junio de 2024. La definición de geodesia se puede explicar como el campo académico de las ciencias de la Tierra que se ocupa de medir y comprender la orientación de la Tierra en el espacio, el campo gravitacional de la Tierra y la forma geométrica de la Tierra. ... La geodesia es una disciplina matemática aplicada que se utiliza para comprender varios aspectos de la Tierra.

[7] "Topógrafos geodésicos". Red de información ocupacional . 26 de noviembre de 2020. Consultado el 28 de enero de 2022 .

[ForoughiTenzer2017-8] Foroughi, Ismael; Tenzer, Robert (2017). "Comparación de diferentes métodos para estimar la separación entre geoide y cuasi-geoide". Revista Geofísica Internacional . 210 (2): 1001–1020. doi : 10.1093/gji/ggx221 . hdl : 10397/75053 . ISSN 0956-540X.

[9] (ISO 19111: Referenciación espacial por coordenadas).

[10] Altamimi, Zuheir; Métivier, Laurent; Rebischung, Paul; Rouby, Hélène; Collilieux, Xavier (junio de 2017). "Modelo de movimiento de placa ITRF2014". Revista Geofísica Internacional . 209 (3): 1906-1912. doi : 10.1093/gji/ggx136 .

[11] Sośnica, Krzysztof; Thaller, Daniela; Dach, Rolf; Jäggi, Adrian; Beutler, Gerhard (agosto de 2013). "Impacto de los desplazamientos de carga en los parámetros derivados del SLR y en la consistencia entre los resultados GNSS y SLR" (PDF) . Journal of Geodesy . 87 (8): 751–769. Bibcode :2013JGeod..87..751S. doi :10.1007/s00190-013-0644-1. S2CID 56017067. Archivado (PDF) desde el original el 2022-03-18.

[12] Zajdel, Radosław; Sośnica, Krzysztof; Enterrar, Grzegorz; Dach, Rolf; Prange, Lars; Kazmierski, Kamil (enero de 2021). "Movimiento polar subdiario de GPS, GLONASS y Galileo". Revista de Geodesia . 95 (1): 3. Bibcode : 2021JGeod..95....3Z. doi : 10.1007/s00190-020-01453-w .

[13] Zajdel, Radosław; Sośnica, Krzysztof; Enterrar, Grzegorz; Dach, Rolf; Prange, Lars (julio de 2020). "Errores sistemáticos específicos del sistema en los parámetros de rotación de la Tierra derivados de GPS, GLONASS y Galileo". Soluciones GPS . 24 (3): 74. Código Bib : 2020GPSS...24...74Z. doi : 10.1007/s10291-020-00989-w .

[14] Zajdel, Radosław; Sośnica, Krzysztof; Bury, Grzegorz (enero de 2021). "Coordenadas del geocentro derivadas de multi-GNSS: una mirada al papel del modelado de la presión de la radiación solar". GPS Solutions . 25 (1): 1. Bibcode :2021GPSS...25....1Z. doi : 10.1007/s10291-020-01037-3 .

[15] Zajdel, R.; Sośnica, K.; Drożdżewski, M.; Bury, G.; Strugarek, D. (noviembre de 2019). "Impacto de la restricción de red en la realización del marco de referencia terrestre basado en observaciones SLR para LAGEOS". Journal of Geodesy . 93 (11): 2293–2313. Bibcode :2019JGeod..93.2293Z. doi : 10.1007/s00190-019-01307-0 .

[16] Sośnica, Krzysztof; Bosy, Jarosław (2019). "Sistema mundial de observación geodésica 2015-2018". Geodesia y Cartografía . doi : 10.24425/gac.2019.126090 .

[17] Pearlman, M.; Arnold, D.; Davis, M.; Barlier, F.; Biancale, R.; Vasiliev, V.; Ciufolini, I.; Paolozzi, A.; Pavlis, EC; Sośnica, K.; Bloßfeld, M. (noviembre de 2019). "Satélites geodésicos láser: una herramienta científica de alta precisión". Revista de Geodesia . 93 (11): 2181–2194. Código Bibliográfico :2019JGeod..93.2181P. doi :10.1007/s00190-019-01228-y. S2CID 127408940.