Precesión

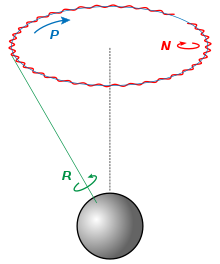
La precesión es un cambio en la orientación del eje de rotación de un cuerpo que gira . En un sistema de referencia adecuado, se puede definir como un cambio en el primer ángulo de Euler , mientras que el tercer ángulo de Euler define la rotación en sí . En otras palabras, si el eje de rotación de un cuerpo está girando alrededor de un segundo eje, se dice que ese cuerpo está precesando alrededor del segundo eje. Un movimiento en el que cambia el segundo ángulo de Euler se llama nutación . En física , hay dos tipos de precesión: sin par y con par.

En astronomía, la precesión se refiere a cualquiera de los cambios lentos que se producen en los parámetros de rotación u órbita de un cuerpo astronómico. Un ejemplo importante es el cambio constante en la orientación del eje de rotación de la Tierra , conocido como precesión de los equinoccios .

La precesión sin par implica que no se aplica ningún momento externo (par) al cuerpo. En la precesión sin par, el momento angular es constante, pero el vector de velocidad angular cambia de orientación con el tiempo. Lo que hace esto posible es un momento de inercia variable en el tiempo , o más precisamente, una matriz de inercia variable en el tiempo . La matriz de inercia está compuesta por los momentos de inercia de un cuerpo calculados con respecto a ejes de coordenadas separados (por ejemplo, x , y , z ). Si un objeto es asimétrico respecto de su eje principal de rotación, el momento de inercia con respecto a cada dirección de coordenadas cambiará con el tiempo, mientras se conserva el momento angular. El resultado es que el componente de las velocidades angulares del cuerpo sobre cada eje variará inversamente con el momento de inercia de cada eje.

La tasa de precesión sin torsión de un objeto con un eje de simetría, como un disco, que gira alrededor de un eje no alineado con ese eje de simetría se puede calcular de la siguiente manera: ^[1] donde ω _p es la tasa de precesión, ω _s es la velocidad de giro alrededor del eje de simetría, I _s es el momento de inercia alrededor del eje de simetría, I _p es el momento de inercia alrededor de cualquiera de los otros dos ejes principales perpendiculares iguales, y α es el ángulo entre la dirección del momento de inercia y el eje de simetría. ^[2]$${\displaystyle {\boldsymbol {\omega }}_{\mathrm {p} }={\frac {{\boldsymbol {I}}_{\mathrm {s} }{\boldsymbol {\omega }}_{\ mathrm {s} }}{{\boldsymbol {I}}_{\mathrm {p} }\cos({\boldsymbol {\alpha }})}}}$$

Cuando un objeto no es perfectamente rígido , la disipación inelástica tenderá a amortiguar la precesión sin torsión, ^[3] y el eje de rotación se alineará con uno de los ejes de inercia del cuerpo.

Para un objeto sólido genérico sin ningún eje de simetría, la evolución de la orientación del objeto, representada (por ejemplo) por una matriz de rotación R que transforma las coordenadas internas en externas, puede simularse numéricamente. Dado el tensor de momento de inercia interno fijo del objeto I ₀ y el momento angular externo fijo L , la velocidad angular instantánea es La precesión se produce al recalcular repetidamente ω y aplicar un pequeño vector de rotación ω dt para el corto tiempo dt ; p. ej.: para la matriz antisimétrica [ ω ] _× . Los errores inducidos por pasos de tiempo finitos tienden a aumentar la energía cinética rotacional: esta tendencia no física puede contrarrestarse aplicando repetidamente un pequeño vector de rotación v perpendicular tanto a ω como a L , observando que$${\displaystyle {\boldsymbol {\omega }}\left({\boldsymbol {R}}\right)={\boldsymbol {R}}{\boldsymbol {I}}_{0}^{-1}{\boldsymbol {R}}^{T}{\boldsymbol {L}}}$$ $${\displaystyle {\boldsymbol {R}}_{\text{nuevo}}=\exp \left(\left[{\boldsymbol {\omega }}\left({\boldsymbol {R}}_{\text{antiguo}}\right)\right]_{\times }dt\right){\boldsymbol {R}}_{\text{antiguo}}}$$ $${\displaystyle E\left({\boldsymbol {R}}\right)={\boldsymbol {\omega }}\left({\boldsymbol {R}}\right)\cdot {\frac {\boldsymbol {L}}{2}}}$$$${\displaystyle E\left(\exp \left(\left[{\boldsymbol {v}}\right]_{\times }\right){\boldsymbol {R}}\right)\approx E\left({\boldsymbol {R}}\right)+\left({\boldsymbol {\omega }}\left({\boldsymbol {R}}\right)\times {\boldsymbol {L}}\right)\cdot {\boldsymbol {v}}}$$

La precesión inducida por par ( precesión giroscópica ) es el fenómeno en el que el eje de un objeto giratorio (por ejemplo, un giroscopio ) describe un cono en el espacio cuando se le aplica un par externo. El fenómeno se observa comúnmente en una peonza de juguete , pero todos los objetos giratorios pueden experimentar precesión. Si la velocidad de rotación y la magnitud del par externo son constantes, el eje de giro se moverá en ángulos rectos a la dirección que intuitivamente resultaría del par externo. En el caso de una peonza de juguete, su peso actúa hacia abajo desde su centro de masa y la fuerza normal (reacción) del suelo lo empuja hacia arriba en el punto de contacto con el soporte. Estas dos fuerzas opuestas producen un par que hace que la peonza precese.

El dispositivo que se muestra a la derecha está montado sobre un cardán . De dentro a fuera hay tres ejes de rotación: el cubo de la rueda, el eje del cardán y el pivote vertical.

Para distinguir entre los dos ejes horizontales, la rotación alrededor del cubo de la rueda se denominará giro y la rotación alrededor del eje del cardán se denominará cabeceo . La rotación alrededor del eje de pivote vertical se denomina rotación .

En primer lugar, imagine que todo el dispositivo gira alrededor del eje de pivote (vertical). A continuación, se añade el giro de la rueda (alrededor del cubo de la rueda). Imagine que el eje del cardán está bloqueado, de modo que la rueda no puede inclinarse. El eje del cardán tiene sensores que miden si hay un par alrededor del eje del cardán.

En la imagen, una sección de la rueda se ha denominado dm ₁ . En el momento representado, la sección dm ₁ está en el perímetro del movimiento giratorio alrededor del eje de pivote (vertical). La sección dm ₁ , por lo tanto, tiene mucha velocidad de rotación angular con respecto a la rotación alrededor del eje de pivote, y como dm ₁ se ve forzada a acercarse al eje de pivote de la rotación (por la rueda que gira más), debido al efecto Coriolis , con respecto al eje de pivote vertical, dm ₁ tiende a moverse en la dirección de la flecha superior izquierda en el diagrama (mostrada a 45°) en la dirección de rotación alrededor del eje de pivote. ^[4] La sección dm ₂ de la rueda se está alejando del eje de pivote, por lo que una fuerza (de nuevo, una fuerza de Coriolis) actúa en la misma dirección que en el caso de dm ₁ . Nótese que ambas flechas apuntan en la misma dirección.

El mismo razonamiento se aplica a la mitad inferior de la rueda, pero allí las flechas apuntan en dirección opuesta a la de las flechas superiores. En conjunto, en toda la rueda, hay un par de torsión alrededor del eje del cardán cuando se suma algo de giro a la rotación alrededor de un eje vertical.

Es importante tener en cuenta que el par alrededor del eje del cardán surge sin ningún retraso; la respuesta es instantánea.

En la discusión anterior, la configuración se mantuvo inalterada al evitar el cabeceo alrededor del eje del cardán. En el caso de una peonza de juguete, cuando la peonza comienza a inclinarse, la gravedad ejerce un par motor. Sin embargo, en lugar de darse vuelta, la peonza simplemente se inclina un poco. Este movimiento de cabeceo reorienta la peonza con respecto al par motor que se está ejerciendo. El resultado es que el par motor ejercido por la gravedad, a través del movimiento de cabeceo, provoca una precesión giroscópica (que a su vez produce un par motor contrario al par motor de la gravedad) en lugar de hacer que la peonza caiga de lado.

La precesión o las consideraciones giroscópicas tienen un efecto en el rendimiento de la bicicleta a alta velocidad. La precesión también es el mecanismo detrás de las brújulas giroscópicas .

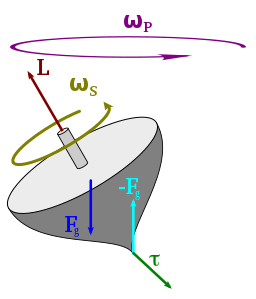
La precesión es el cambio de velocidad angular y momento angular producido por un par. La ecuación general que relaciona el par con la tasa de cambio del momento angular es: donde y son los vectores de par y momento angular respectivamente.$${\displaystyle {\boldsymbol {\tau }}={\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}}$$${\displaystyle {\boldsymbol {\tau }}}$${\displaystyle \mathbf {L}}$

Debido a la forma en que se definen los vectores de par, se trata de un vector perpendicular al plano de las fuerzas que lo crean. Por lo tanto, se puede observar que el vector de momento angular cambiará perpendicularmente a esas fuerzas. Dependiendo de cómo se creen las fuerzas, a menudo rotarán con el vector de momento angular y, luego, se creará la precesión circular.

En estas circunstancias la velocidad angular de precesión viene dada por: ^[5]

${\displaystyle {\boldsymbol {\omega }}_{\mathrm {p} }={\frac {\ mgr}{I_{\mathrm {s} }{\boldsymbol {\omega }}_{\mathrm {s } }}}={\frac {\tau }{I_{\mathrm {s} }{\boldsymbol {\omega }}_{\mathrm {s} }\sin(\theta )}}}$

donde I _s es el momento de inercia , ω _s es la velocidad angular de giro sobre el eje de giro, m es la masa, g es la aceleración debida a la gravedad, θ es el ángulo entre el eje de giro y el eje de precesión y r es la distancia entre el centro de masa y el pivote. El vector de torsión se origina en el centro de masa. Usando ω = ⁠2π/yo⁠ , encontramos que el período de precesión está dado por: ^[6]$${\displaystyle T_{\mathrm {p} }={\frac {4\pi ^{2}I_{\mathrm {s} }}{\ mgrT_{\mathrm {s} }}}={\frac {4\pi ^{2}I_{\mathrm {s} }\sin(\theta )}{\ \tau T_{\mathrm {s} }}}}$$

Donde I _s es el momento de inercia , T _s es el período de giro alrededor del eje de giro y τ es el par . Sin embargo, en general, el problema es más complicado que esto.

Las teorías de la relatividad especial y general ofrecen tres tipos de correcciones a la precesión newtoniana de un giroscopio cerca de una gran masa como la Tierra, descrita anteriormente. Son:

• Precesión de Thomas , una corrección relativista especial que tiene en cuenta un objeto (como un giroscopio) que se acelera a lo largo de una trayectoria curva.
• precesión de De Sitter , una corrección relativista general que tiene en cuenta la métrica de Schwarzschild del espacio curvo cerca de una gran masa no giratoria.
• Precesión Lense-Thirring , una corrección relativista general que tiene en cuenta el arrastre del marco mediante la métrica de Kerr del espacio curvo cerca de una gran masa giratoria.

La geodésica de Schwarzschild (a veces llamada precesión de Schwarzschild) se utiliza para predecir la precesión anómala del perihelio de los planetas, sobre todo para predecir con precisión la precesión absidal de Mercurio.

En astronomía, la precesión se refiere a cualquiera de los diversos cambios lentos y continuos inducidos por la gravedad en el eje de rotación o la trayectoria orbital de un cuerpo astronómico. La precesión de los equinoccios, la precesión del perihelio, los cambios en la inclinación del eje de la Tierra respecto de su órbita y la excentricidad de su órbita a lo largo de decenas de miles de años son partes importantes de la teoría astronómica de las eras glaciales . (Véase ciclos de Milankovitch .)

La precesión axial es el movimiento del eje de rotación de un cuerpo astronómico, por el cual el eje traza lentamente un cono. En el caso de la Tierra, este tipo de precesión también se conoce como precesión de los equinoccios , precesión lunisolar o precesión del ecuador . La Tierra pasa por un ciclo de precesión completo en un período de aproximadamente 26.000 años o 1° cada 72 años, durante el cual las posiciones de las estrellas cambiarán lentamente tanto en coordenadas ecuatoriales como en longitud eclíptica . Durante este ciclo, el polo axial norte de la Tierra se mueve desde donde está ahora, a 1° de Polaris , en un círculo alrededor del polo eclíptico , con un radio angular de aproximadamente 23,5°.

El astrónomo griego antiguo Hiparco (c. 190-120 a. C.) es generalmente aceptado como el primer astrónomo conocido en reconocer y evaluar la precesión de los equinoccios en aproximadamente 1° por siglo (que no está lejos del valor real para la antigüedad, 1,38°), ^[7] aunque hay una pequeña disputa sobre si lo fue. ^[8] En la antigua China , el erudito y funcionario de la dinastía Jin Yu Xi ( fl. 307-345 d. C.) hizo un descubrimiento similar siglos después, al notar que la posición del Sol durante el solsticio de invierno se había desplazado aproximadamente un grado en el transcurso de cincuenta años en relación con la posición de las estrellas. ^[9] La precesión del eje de la Tierra fue explicada más tarde por la física newtoniana . Al ser un esferoide achatado , la Tierra tiene una forma no esférica, abultándose hacia afuera en el ecuador. Las fuerzas de marea gravitatorias de la Luna y el Sol ejercen un par de torsión sobre el ecuador, intentando empujar el abultamiento ecuatorial hacia el plano de la eclíptica , pero en lugar de ello provocan su precesión. El par de torsión ejercido por los planetas, en particular Júpiter , también desempeña un papel. ^[10]

Las órbitas de los planetas alrededor del Sol no siguen en realidad una elipse idéntica cada vez, sino que en realidad trazan una forma de pétalo de flor, porque el eje mayor de la órbita elíptica de cada planeta también precesa dentro de su plano orbital, en parte como respuesta a perturbaciones en forma de fuerzas gravitacionales cambiantes ejercidas por otros planetas. Esto se llama precesión del perihelio o precesión absidal .

En la imagen adjunta se ilustra la precesión absidal de la Tierra. A medida que la Tierra se desplaza alrededor del Sol, su órbita elíptica rota gradualmente con el tiempo. La excentricidad de su elipse y la velocidad de precesión de su órbita están exageradas para facilitar su visualización. La mayoría de las órbitas del Sistema Solar tienen una excentricidad mucho menor y precesan a un ritmo mucho más lento, lo que las hace casi circulares y casi estacionarias.

Las discrepancias entre la tasa de precesión del perihelio observada del planeta Mercurio y la predicha por la mecánica clásica fueron prominentes entre las formas de evidencia experimental que llevaron a la aceptación de la Teoría de la Relatividad de Einstein (en particular, su Teoría General de la Relatividad ), que predijo con precisión las anomalías. ^{[11] [12]} Desviándose de la ley de Newton, la teoría de la gravitación de Einstein predice un término adicional de ⁠A/r4^​⁠ , lo que arroja con precisión el exceso de velocidad de giro observado de 43 segundos de arco cada 100 años.

Los nodos orbitales también precesan con el tiempo.

• Precesión de Larmor
• Inclinación
• Movimiento polar
• Precesión (mecánica)
• La precesión como forma de transporte paralelo

Wikilibros tiene un libro sobre el tema: Movimiento de rotación

• Medios relacionados con Precesión en Wikimedia Commons
• Explicación y derivación de la fórmula para la precesión de un trompo.
• La precesión y la teoría de Milankovich De astrónomos a naves espaciales