Resolución cinética
Método de separación de enantiómeros en una mezcla racémica por velocidad de reacción

En química orgánica , la resolución cinética es un medio para diferenciar dos enantiómeros en una mezcla racémica . En la resolución cinética, dos enantiómeros reaccionan con diferentes velocidades de reacción en una reacción química con un catalizador o reactivo quiral , lo que da como resultado una muestra enantioenriquecida del enantiómero menos reactivo. [1] A diferencia de la resolución quiral , la resolución cinética no se basa en diferentes propiedades físicas de los productos diastereoméricos, sino en las diferentes propiedades químicas de los materiales de partida racémicos. El exceso enantiomérico (ee) del material de partida que no reaccionó aumenta continuamente a medida que se forma más producto, alcanzando el 100% justo antes de que se complete la reacción. La resolución cinética se basa en las diferencias de reactividad entre enantiómeros o complejos enantioméricos.

La resolución cinética se puede utilizar para la preparación de moléculas quirales en la síntesis orgánica . Las reacciones de resolución cinética que utilizan reactivos y catalizadores puramente sintéticos son mucho menos comunes que el uso de la resolución cinética enzimática en aplicaciones para la síntesis orgánica, aunque en los últimos 30 años se han desarrollado varias técnicas sintéticas útiles. [2]

Historia

La primera resolución cinética de la que se tiene conocimiento fue lograda por Louis Pasteur . Después de hacer reaccionar tartrato de amonio racémico acuoso con un moho de Penicillium glaucum, volvió a aislar el tartrato restante y descubrió que era levógiro . [3] Los microorganismos quirales presentes en el moho catalizaron la metabolización de ( R , R )-tartrato de forma selectiva, dejando un exceso de ( S , S )-tartrato.

La resolución cinética por medios sintéticos fue descrita por primera vez por Marckwald y McKenzie en 1899 en la esterificación del ácido mandélico racémico con (−)- mentol ópticamente activo . Con un exceso de ácido racémico presente, observaron que la formación del éster derivado del (+)- ácido mandélico era más rápida que la formación del éster del (−)-ácido mandélico. Se observó que el ácido que no reaccionó tenía un ligero exceso de (−)-ácido mandélico, y más tarde se demostró que el éster producía (+)-ácido mandélico tras la saponificación. La importancia de esta observación fue que, en teoría, si se hubiera utilizado medio equivalente de (−)-mentol, se podría haber preparado una muestra altamente enantioenriquecida de (−)-ácido mandélico. Esta observación condujo a la resolución cinética exitosa de otros ácidos quirales, el comienzo del uso de la resolución cinética en química orgánica. [4] [5]

Teoría

La resolución cinética es un método posible para diferenciar irreversiblemente un par de enantiómeros debido a energías de activación (potencialmente) diferentes. Si bien ambos enantiómeros tienen el mismo nivel de energía libre de Gibbs por definición, y los productos de la reacción con ambos enantiómeros también tienen niveles iguales, la energía del estado de transición puede diferir. En la imagen de abajo, el enantiómero R tiene una energía de activación más baja y, por lo tanto, reaccionaría más rápido que el enantiómero S. Δ GRAMO ‡ {\displaystyle \Delta G^{\ddagger }} Δ GRAMO ‡ {\displaystyle \Delta G^{\ddagger }}

Diagrama de energía libre de Gibbs

La resolución cinética ideal es aquella en la que solo reacciona un enantiómero, es decir, k R >> k S . La selectividad (s) de una resolución cinética está relacionada con las constantes de velocidad de la reacción de los enantiómeros R y S, k R y k S respectivamente, por s=k R /k S , para k R >k S . Esta selectividad también puede denominarse velocidades relativas de reacción . Esto puede escribirse en términos de la diferencia de energía libre entre los estados de transición de alta y baja energía, . [6] Δ Δ GRAMO ‡ {\displaystyle \Delta \Delta G^{\ddagger }}

s = a R a S = mi Δ Δ GRAMO ‡ / R yo {\displaystyle s={\frac {k_{R}}{k_{S}}}=e^{\Delta \Delta G^{\ddagger }/RT}}

La selectividad también se puede expresar en términos de ee del material de partida recuperado y la conversión (c), si se supone una cinética de primer orden (en el sustrato). Si se supone que el enantiómero S del racemato del material de partida se recuperará en exceso, es posible expresar las concentraciones (fracciones molares) de los enantiómeros S y R como

[ S ] = ( 1 + mi mi ) ( 1 − do ) 2 {\displaystyle [S]={\frac {(1+ee)(1-c)}{2}}}
[ R ] = ( 1 − mi mi ) ( 1 − do ) 2 {\displaystyle [R]={\frac {(1-ee)(1-c)}{2}}}

donde ee es el ee del material de partida. Nótese que para c=0, que significa el comienzo de la reacción, , donde estos significan las concentraciones iniciales de los enantiómeros. Entonces, para el agente de resolución quiral estequiométrico B*, S 0 = R 0 = 1 2 {\displaystyle S_{0}=R_{0}={\frac {1}{2}}}

d [ S ] d a = − a S [ S ] [ B ∗ ] ⟹ registro ⁡ [ S ] = − a S [ B ∗ ] a + registro ⁡ S 0 {\displaystyle {\frac {d[S]}{dt}}=-k_{S}[S][B^{*}]\implies \log[S]=-k_{S}[B^{*}]t+\log S_{0}}

Nótese que, si el agente de resolución es estequiométrico y aquiral, con un catalizador quiral, el término [B*] no aparece. En cualquier caso, con una expresión similar para R, podemos expresar s como

s = a R a S = registro ⁡ [ R ] − registro ⁡ R 0 registro ⁡ [ S ] − registro ⁡ S 0 = registro ⁡ [ ( 1 − do ) ( 1 − mi mi ) ] + registro ⁡ 1 2 − registro ⁡ R 0 registro ⁡ [ ( 1 − do ) ( 1 + mi mi ) ] + registro ⁡ 1 2 − registro ⁡ S 0 = registro ⁡ [ ( 1 − do ) ( 1 − mi mi ) ] registro ⁡ [ ( 1 − do ) ( 1 + mi mi ) ] {\displaystyle s={\frac {k_{R}}{k_{S}}}={\frac {\log[R]-\log R_{0}}{\log[S]-\log S_{0}}}={\frac {\log[(1-c)(1-ee)]+\log {\frac {1}{2}}-\log R_{0}}{\log[(1-c)(1+ee)]+\log {\frac {1}{2}}-\log S_{0}}}={\frac {\log[(1-c)(1-ee)]}{\log[(1-c)(1+ee)]}}}

Si deseamos expresar esto en términos del exceso enantiomérico del producto, ee", debemos hacer uso del hecho de que, para los productos R' y S' de R y S, respectivamente

e e ″ = [ R ′ ] − [ S ′ ] [ R ′ ] + [ S ′ ] = e e ( 1 − c ) c ⟹ e e = e e ″ c 1 − c {\displaystyle ee''={\frac {[R']-[S']}{[R']+[S']}}={\frac {ee(1-c)}{c}}\implies ee=ee''{\frac {c}{1-c}}}

Desde aquí vemos que

1 − e e = 1 − c − c e e ″ 1 − c {\displaystyle 1-ee={\frac {1-c-cee''}{1-c}}}
1 + e e = 1 − c + c e e ″ 1 − c {\displaystyle 1+ee={\frac {1-c+cee''}{1-c}}}

lo que nos da

( 1 − c ) ( 1 − e e ) = 1 − c ( 1 + e e ″ ) {\displaystyle (1-c)(1-ee)=1-c(1+ee'')}
( 1 − c ) ( 1 + e e ) = 1 − c ( 1 − e e ″ ) {\displaystyle (1-c)(1+ee)=1-c(1-ee'')}

que, cuando lo introducimos en nuestra expresión para s derivada anteriormente, da como resultado

s = log ⁡ [ 1 − c ( 1 + e e ″ ) ] log ⁡ [ 1 − c ( 1 − e e ″ ) ] {\displaystyle s={\frac {\log[1-c(1+ee'')]}{\log[1-c(1-ee'')]}}}

El factor de conversión ( c ) y el factor de selectividad ( s ) se pueden expresar únicamente en términos de excesos enantioméricos del material de partida y del producto (ee y ee'', respectivamente):

c = e e e e + e e ″ ⟹ s = log ⁡ [ ( e e ″ − e e ⋅ e e ″ ) / ( e e + e e ″ ) ] log ⁡ [ ( e e ″ + e e ⋅ e e ″ ) / ( e e + e e ″ ) ] {\displaystyle c={\frac {ee}{ee+ee''}}\implies s={\frac {\log[(ee''-ee\cdot ee'')/(ee+ee'')]}{\log[(ee''+ee\cdot ee'')/(ee+ee'')]}}}

Además, las expresiones para c y ee se pueden parametrizar para dar expresiones explícitas para C y ee en términos de t. Primero, al resolver explícitamente [S] y [R] como funciones de t se obtiene

d [ S ] d t = − k S [ S ] ⟹ S = 1 2 e − k S t {\displaystyle {\frac {d[S]}{dt}}=-k_{S}[S]\implies S={\frac {1}{2}}e^{-k_{S}t}}

que, insertado en expresiones para ee y c, da

e e = [ S ] − [ R ] [ S ] + [ R ] = e − k S t − e − k R t e − k S t + e − k R t {\displaystyle ee={\frac {[S]-[R]}{[S]+[R]}}={\frac {e^{-k_{S}t}-e^{-k_{R}t}}{e^{-k_{S}t}+e^{-k_{R}t}}}}
c = 1 − ( [ S ] − [ R ] ) = 1 − e − k S t + e − k R t 2 {\displaystyle c=1-{\big (}[S]-[R]{\big )}=1-{\frac {e^{-k_{S}t}+e^{-k_{R}t}}{2}}}

Sin pérdida de generalidad, podemos permitir que k S = 1, lo que da k R = s, simplificando las expresiones anteriores. De manera similar, se puede derivar una expresión para ee″ como función de t

e e ″ = 1 − c c e e = e − t + e − s t 2 − e − t − e − s t ( e − t − e − s t e − t + e − s t ) {\displaystyle ee''={\frac {1-c}{c}}ee={\frac {e^{-t}+e^{-st}}{2-e^{-t}-e^{-st}}}\left({\frac {e^{-t}-e^{-st}}{e^{-t}+e^{-st}}}\right)}

De esta forma, se pueden generar gráficos de ee y ee″ vs. c con t como parámetro y diferentes valores de s generando diferentes curvas, como se muestra a continuación.

Como se puede observar, los excesos enantioméricos elevados son mucho más fáciles de conseguir para el material de partida que no ha reaccionado. Sin embargo, existe una compensación entre ee y conversión, ya que se obtiene un ee más alto (del sustrato recuperado) con una conversión más alta y, por lo tanto, un rendimiento aislado más bajo. Por ejemplo, con un factor de selectividad de solo 10, es posible un 99 % de ee con una conversión de aproximadamente el 70 %, lo que da como resultado un rendimiento de aproximadamente el 30 %. Por el contrario, para obtener buenos ee y un buen rendimiento del producto, se necesitan factores de selectividad muy altos. Por ejemplo, con un factor de selectividad de 10, es inalcanzable un ee″ superior al 80 % aproximadamente, y se obtienen valores de ee″ significativamente más bajos para conversiones más realistas. Se requiere una selectividad superior a 50 para un producto altamente enantioenriquecido, con un rendimiento razonable.

Esta es una versión simplificada de la cinética real de la resolución cinética. La suposición de que la reacción es de primer orden en el sustrato es limitante, y es posible que la dependencia del sustrato pueda depender de la conversión, lo que da como resultado un panorama mucho más complicado. Como resultado, un enfoque común es medir e informar solo los rendimientos y los ee, ya que la fórmula para k rel solo se aplica a una resolución cinética idealizada. Es simple considerar la formación de un complejo sustrato-catalizador inicial, lo que podría negar la cinética de primer orden. Sin embargo, las conclusiones generales extraídas siguen siendo útiles para comprender el efecto de la selectividad y la conversión en los ee.

Sentido práctico

Con la llegada de la catálisis asimétrica , es necesario considerar la viabilidad de utilizar la resolución cinética para la preparación de productos enantiopuros. Incluso para un producto que se puede obtener a través de una ruta catalítica asimétrica o basada en auxiliares, el racemato puede ser significativamente menos costoso que el material enantiopuro, lo que resulta en una mayor rentabilidad incluso con la "pérdida" inherente del 50% del material. Se han propuesto las siguientes condiciones necesarias para una resolución cinética práctica: [6]

  • Racemato y catalizador económicos
  • No es posible ninguna ruta de resolución enantioselectiva, de grupo quiral o clásica apropiada
  • La resolución se produce de forma selectiva con cargas bajas de catalizador.
  • La separación del material de partida y el producto es fácil.

Hasta la fecha, se han desarrollado varios catalizadores para la resolución cinética que satisfacen la mayoría de los criterios anteriores, si no todos, lo que los hace muy prácticos para su uso en la síntesis orgánica. En las siguientes secciones se analizarán varios ejemplos clave.

Reacciones que utilizan reactivos sintéticos

Reacciones de acilación

Catalizador DMAP (-) quiral planar de Fu para la resolución cinética de alcoholes secundarios

Gregory Fu y sus colegas han desarrollado una metodología que utiliza un análogo quiral de DMAP para lograr una excelente resolución cinética de alcoholes secundarios. [7] Los estudios iniciales que utilizaron éter como disolvente, cargas bajas de catalizador (2% molar), anhídrido acético como agente acilante y trietilamina a temperatura ambiente dieron selectividades que oscilaban entre 14 y 52, lo que corresponde a ee del producto de alcohol recuperado de hasta 99,2%. [8] Sin embargo, la detección de disolventes demostró que el uso de alcohol terc-amílico aumentó tanto la reactividad como la selectividad. [9]

Con el sustrato de referencia 1-feniletanol, esto correspondió a un 99 % de ee del alcohol sin reaccionar con una conversión del 55 % cuando se lo ejecutó a 0 °C. Este sistema demostró ser apto para la resolución de varios arilalquilcarbinoles, con selectividades tan altas como 95 y cargas bajas de catalizador del 1 %, como se muestra a continuación utilizando el enantiómero (-) del catalizador. Esto dio como resultado alcoholes altamente enantioenriquecidos con conversiones muy bajas, lo que también dio excelentes rendimientos. Además, las altas selectividades dan como resultado productos acilados altamente enantioenriquecidos, con una muestra de 90 % de ee de alcohol acilado para o-tolilmetilcarbinol, con s = 71.

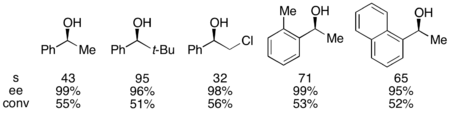
Además, Fu informó sobre la primera acilación altamente selectiva de dioles racémicos (así como la desimetrización de dioles meso). Con una carga de catalizador baja del 1%, se recuperó el diol enantioenriquecido con un 98% de ee y un rendimiento del 43%, y el diacetato con un rendimiento del 39% y un 99% de ee. El resto del material se recuperó como una mezcla de monoacetato.

También se demostró que el catalizador DMAP planar-quiral es eficaz para resolver cinéticamente alcoholes propargílicos . [10] En este caso, sin embargo, se encontró que las selectividades eran más altas sin ninguna base presente. Cuando se utilizó 1 mol % del catalizador a 0 °C, se pudieron alcanzar selectividades de hasta 20. Las limitaciones de este método incluyen el requisito de una funcionalidad insaturada, como carbonilo o alquenos, en la posición alquinilo remota. Los alcoholes resueltos utilizando el enantiómero (+) del catalizador DMAP se muestran a continuación.

Fu también demostró la capacidad de su catalizador DMAP quiral para resolver alcoholes alílicos . [11] La selectividad efectiva dependía de la presencia de un sustituyente geminal o cis en el grupo que contenía el alcohol, con una notable excepción de un alcohol trans-fenilo que exhibió la selectividad más alta. Utilizando entre 1 y 2,5 mol % del enantiómero (+) del catalizador DMAP, los alcoholes que se muestran a continuación se resolvieron en presencia de trietilamina.

El catalizador (-)-PPY* de Fu (izquierda) y el nuevo agente acilante (derecha)

Si bien el catalizador análogo DMAP de Fu funcionó excepcionalmente bien para resolver cinéticamente alcoholes racémicos, no tuvo éxito en su uso para la resolución cinética de aminas. Se desarrolló un catalizador similar, PPY*, que, en uso con un nuevo agente acilante, permitió la acilación con resolución cinética exitosa de aminas. Con 10 mol% de (-)-PPY* en cloroformo a –50 °C, se observaron selectividades buenas a muy buenas en la acilación de aminas, como se muestra a continuación. [12] Se desarrolló un protocolo similar para la resolución cinética de indolinas. [13]

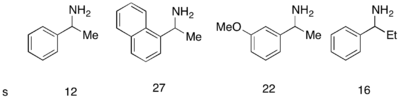
Epoxidaciones y dihidroxilaciones

La epoxidación de Sharpless , desarrollada por K. Barry Sharpless en 1980, [14] se ha utilizado para la resolución cinética de una mezcla racémica de alcoholes alílicos. [15] [16] Si bien es extremadamente eficaz para resolver varios alcoholes alílicos, este método tiene una serie de desventajas. Los tiempos de reacción pueden durar hasta 6 días y el catalizador no es reciclable. Sin embargo, la resolución cinética de epoxidación asimétrica de Sharpless sigue siendo una de las resoluciones cinéticas sintéticas más efectivas hasta la fecha. Se pueden utilizar varios tartratos diferentes para el catalizador; a continuación se muestra un esquema representativo que utiliza tartrato de diisopropilo . Este método se ha utilizado de forma generalizada en varios alcoholes alílicos secundarios. [17]

La dihidroxilación asimétrica de Sharpless también se ha utilizado como método para la resolución cinética. [18] [19] Sin embargo, este método no se utiliza ampliamente, ya que la misma resolución se puede lograr de diferentes maneras que son más económicas. Además, se ha demostrado que la epoxidación de Shi afecta la resolución cinética de una selección limitada de olefinas. [20] Este método tampoco se utiliza ampliamente, pero es de interés mecanicista.

Aberturas de epóxido

Catalizador de (R,R) (salen)-Cr de Jacobsen para la resolución cinética de epóxidos terminales mediante la formación de azida

Aunque se han logrado epoxidaciones enantioselectivas con éxito utilizando epoxidación de Sharpless, epoxidación de Shi y epoxidación de Jacobsen , ninguno de estos métodos permite la síntesis asimétrica eficiente de epóxidos terminales, que son bloques de construcción quirales clave. Debido al bajo costo de la mayoría de los epóxidos terminales racémicos y su incapacidad para ser generalmente sometidos a resolución clásica, una resolución cinética efectiva de epóxidos terminales serviría como una metodología sintética muy importante. En 1996, Jacobsen y colaboradores desarrollaron una metodología para la resolución cinética de epóxidos a través de la apertura de anillo nucleófilo con ataque por un anión azida. Se muestra el catalizador (R,R). [21] El catalizador podría efectivamente, con cargas tan bajas como 0,5 mol%, abrir el epóxido en la posición terminal enantioselectivamente, produciendo material de partida de epóxido enantioenriquecido y alcoholes 1,2-azido. Los rendimientos son casi cuantitativos y los ee fueron excelentes (≥95% en casi todos los casos). Los alcoholes 1,2-azido se pueden hidrogenar para dar alcoholes 1,2-amino, como se muestra a continuación.

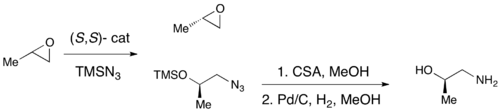
Catalizador de (R,R) (salen)-Cr de Jacobsen para la resolución cinética hidrolítica de epóxidos terminales

En 1997, el grupo de Jacobsen publicó una metodología que mejoraba su trabajo anterior, permitiendo el uso de agua como nucleófilo en la apertura del epóxido. Utilizando un catalizador casi idéntico, se observaron ee superiores al 98% tanto para el epóxido de partida recuperado como para el producto 1,2-diol. En el ejemplo siguiente, la resolución cinética hidrolítica (HKR) se llevó a cabo en una escala de 58 gramos, lo que dio como resultado 26 g (44%) del epóxido enantiorificado en >99% ee y 38 g (50%) del diol en 98% ee. [22]

Se examinaron muchos otros sustratos, con rendimientos del epóxido recuperado que oscilaron entre el 36 y el 48 % para un ee >99 %. La resolución cinética hidrolítica de Jacobsen se puede utilizar en conjunto con la epoxidación de Jacobsen para producir epóxidos enantiopuros a partir de ciertas olefinas, como se muestra a continuación. La primera epoxidación produce un epóxido ligeramente enantioenriquecido, y la resolución cinética posterior produce esencialmente un solo enantiómero. La ventaja de este enfoque es la capacidad de reducir la cantidad de escisión hidrolítica necesaria para lograr una alta enantioselectividad, lo que permite rendimientos generales de hasta aproximadamente el 90 %, en función de la olefina. [23]

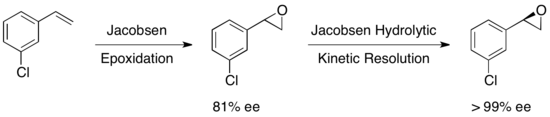
En definitiva, las resoluciones cinéticas de apertura de epóxidos de Jacobsen producen una alta pureza enantiomérica en el epóxido y el producto, en condiciones libres de disolventes o con bajo contenido de disolventes, y han sido aplicables a gran escala. La metodología de Jacobsen para HKR en particular es extremadamente atractiva, ya que se puede llevar a cabo en una escala de varias toneladas y utiliza agua como nucleófilo, lo que da como resultado procesos industriales extremadamente rentables. A pesar de los impresionantes logros, HKR se ha aplicado generalmente a la resolución de epóxidos terminales simples con un estereocentro. Muy recientemente, DA Devalankar et al. informaron un protocolo elegante que implica un HKR cocatalizado con dos estereocentros de epóxidos terminales racémicos que tienen sustituyentes de unión C–C adyacentes. [24]

Oxidaciones

Catalizador (S,S) de Noyori para la hidrogenación por transferencia/resolución cinética de alcoholes secundarios

Ryōji Noyori y sus colegas han desarrollado una metodología para la resolución cinética de alcoholes secundarios bencílicos y alílicos mediante hidrogenación por transferencia. El complejo de rutenio cataliza la oxidación del enantiómero más reactivo de la acetona , lo que produce un alcohol enantiopuro sin reaccionar, una cetona oxidada e isopropanol. En el ejemplo ilustrado a continuación, la exposición de 1-feniletanol al enantiómero (S,S) del catalizador en presencia de acetona da como resultado un rendimiento del 51% de 94% de ee (R)-1-feniletanol, junto con 49% de acetofenona e isopropanol como subproducto. [25]

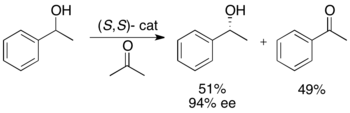
Esta metodología es esencialmente la inversa de la hidrogenación de cetonas por transferencia asimétrica de Noyori [26] , que produce alcoholes enantioenriquecidos mediante reducción. Esto limita el atractivo del método de resolución cinética, ya que existe un método similar para lograr los mismos productos sin la pérdida de la mitad del material. Por lo tanto, la resolución cinética solo se llevaría a cabo en un caso en el que el alcohol racémico fuera al menos la mitad del precio de la cetona o significativamente más fácil de acceder.

Catalizador de Uemura y Hidai para hidrogenación por transferencia/resolución cinética de alcoholes secundarios

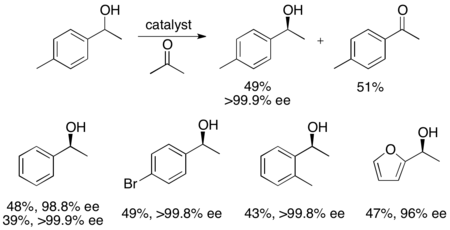
Además, Uemura y Hidai han desarrollado un catalizador de rutenio para la oxidación por resolución cinética de alcoholes bencílicos, produciendo alcoholes altamente enantioenriquecidos con buenos rendimientos. [27] El complejo puede, como el catalizador de Noyori, afectar la hidrogenación por transferencia entre una cetona e isopropanol para dar un alcohol enantioenriquecido, así como afectar la resolución cinética de un alcohol racémico, dando alcohol enantiopuro (>99% ee) y cetona oxidada, con acetona como subproducto. Es muy eficaz para reducir cetonas enantioselectivamente, dando la mayoría de los alcoholes bencílicos en >99% ee y puede resolver varios alcoholes bencílicos racémicos para dar altos rendimientos (hasta 49%) de enantiómeros individuales, como se muestra a continuación. Este método tiene las mismas desventajas que la resolución cinética de Noyori, es decir, que también se puede acceder a los alcoholes mediante la reducción de las cetonas enantioselectivamente. Además, sólo se ha informado de un enantiómero del catalizador.

Hidrogenación

Catalizador (R)-BINAP Ru de Noyori para la resolución cinética hidrogenativa de alcoholes alílicos

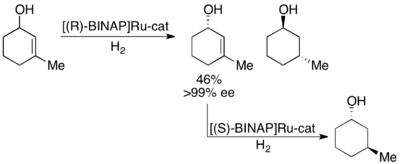
Noyori también ha demostrado la resolución cinética de alcoholes alílicos mediante hidrogenación asimétrica de la olefina. [28] Utilizando el complejo Ru[BINAP], la hidrogenación selectiva puede dar altos ee del alcohol insaturado además del alcohol hidrogenado, como se muestra a continuación. Por lo tanto, una segunda hidrogenación del alcohol alílico enantioenriquecido restante dará muestras enantioméricamente puras de ambos enantiómeros del alcohol saturado. Noyori ha resuelto una serie de alcoholes alílicos con rendimientos buenos a excelentes y ee buenos a excelentes (hasta >99%).

Metátesis de cierre de anillo

Resolución cinética del catalizador de Hoveyda y Schrock para la metátesis de cierre de anillo

Hoveyda y Schrock han desarrollado un catalizador para la resolución cinética de metátesis de cierre de anillo de alcoholes alílicos dienílicos. [29] El catalizador de alquilideno de molibdeno cataliza selectivamente un enantiómero para realizar la metátesis de cierre de anillo, lo que da como resultado un alcohol enantiopuro y un anillo cerrado enantiopuro, como se muestra a continuación. El catalizador es más eficaz para resolver 1,6-dienos. Sin embargo, ligeros cambios estructurales en el sustrato, como aumentar la distancia entre alquenos a 1,7, a veces pueden requerir el uso de un catalizador diferente, lo que reduce la eficacia de este método.

Reacciones enzimáticas

Acilaciones

Al igual que con los procedimientos de resolución cinética sintética, las resoluciones cinéticas de acilación enzimática han visto la aplicación más amplia en un contexto sintético. Especialmente importante ha sido el uso de la resolución cinética enzimática para preparar aminoácidos de manera eficiente y económica. A escala comercial, la metodología de Degussa que emplea acilasas es capaz de resolver numerosos aminoácidos naturales y no naturales. Las mezclas racémicas se pueden preparar mediante síntesis de Strecker , y el uso de acilasa de riñón porcino (para sustratos de cadena lineal) o una enzima del moho Aspergillus oryzae (para sustratos de cadena lateral ramificada) puede producir de manera efectiva aminoácidos enantioenriquecidos en rendimientos altos (85-90%). El material de partida sin reaccionar se puede racemizar in situ, lo que hace que esta sea una resolución cinética dinámica. [30]

Además, las lipasas se utilizan ampliamente para la resolución cinética tanto en entornos académicos como industriales. [31] [32] Las lipasas se han utilizado para resolver alcoholes primarios, alcoholes secundarios, un número limitado de alcoholes terciarios, ácidos carboxílicos, dioles e incluso alenos quirales. La lipasa de Pseudomonas cepacia (PSL) es la más utilizada en la resolución de alcoholes primarios y se ha utilizado con acetato de vinilo como agente acilante para resolver cinéticamente los alcoholes primarios que se muestran a continuación.

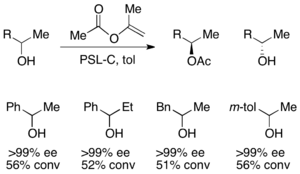
Para la resolución de alcoholes secundarios, se ha empleado eficazmente la lipasa de pseudomonas cepecia (PSL-C) para generar excelentes ee del enantiómero ( R ) del alcohol. [33] El uso de acetato de isopropenilo como agente acilante da como resultado acetona como subproducto, que se elimina eficazmente de la reacción utilizando tamices moleculares .

Oxidaciones y reducciones

La levadura de panadería (BY) se ha utilizado para la resolución cinética de compuestos carbonílicos α-estereogénicos. [34] [35] La enzima reduce selectivamente un enantiómero, produciendo un alcohol y una cetona altamente enantioenriquecidos, como se muestra a continuación.

La levadura de panadería también se ha utilizado en la resolución cinética de alcoholes bencílicos secundarios por oxidación. [36] Si bien se han informado excelentes ee del alcohol recuperado, generalmente requieren una conversión de >60 %, lo que da como resultado rendimientos disminuidos. La levadura de panadería también se ha utilizado en la resolución cinética mediante la reducción de β-cetoésteres. [37] Sin embargo, dado el éxito de la resolución de Noyori de los mismos sustratos, que se detalla más adelante en este artículo, esto no ha tenido mucho uso.

Resolución cinética dinámica

La resolución cinética dinámica (DKR) ocurre cuando el racemato del material de partida puede epimerizarse fácilmente, lo que da como resultado una mezcla de material de partida esencialmente racémica en todos los puntos durante la reacción. Entonces, el enantiómero con la barrera más baja para la activación puede formarse, teóricamente, con un rendimiento de hasta el 100%. Esto contrasta con la resolución cinética estándar, que necesariamente tiene un rendimiento máximo del 50%. Por esta razón, la resolución cinética dinámica tiene aplicaciones extremadamente prácticas para la síntesis orgánica. La dinámica observada se basa en el principio de Curtin-Hammett . La barrera para la reacción de cualquiera de los enantiómeros es necesariamente más alta que la barrera para la epimerización, lo que da como resultado un pozo cinético que contiene el racemato. Esto es equivalente a escribir, para k R >k S ,

Δ G r a c < Δ G R ‡ < Δ G S ‡ {\displaystyle \Delta G_{rac}<\Delta G_{R}^{\ddagger }<\Delta G_{S}^{\ddagger }}

Se han publicado varias revisiones excelentes, la más reciente en 2008, que detallan la teoría y las aplicaciones prácticas del DKR. [38] [39] [40]

Hidrogenación asimétrica de Noyori

La hidrogenación asimétrica de cetonas de Noyori es un excelente ejemplo de resolución cinética dinámica en funcionamiento. Los β-cetoésteres enantioméricos pueden sufrir epimerización , y la elección del catalizador quiral, típicamente de la forma Ru[(R)-BINAP]X 2 , donde X es un halógeno , lleva a que uno de los enantiómeros reaccione preferentemente más rápido. La energía libre relativa para una reacción representativa se muestra a continuación. [41] [42] Como se puede ver, el intermedio de epimerización tiene menor energía libre que los estados de transición para la hidrogenación, lo que resulta en una racemización rápida y altos rendimientos de un solo enantiómero del producto.

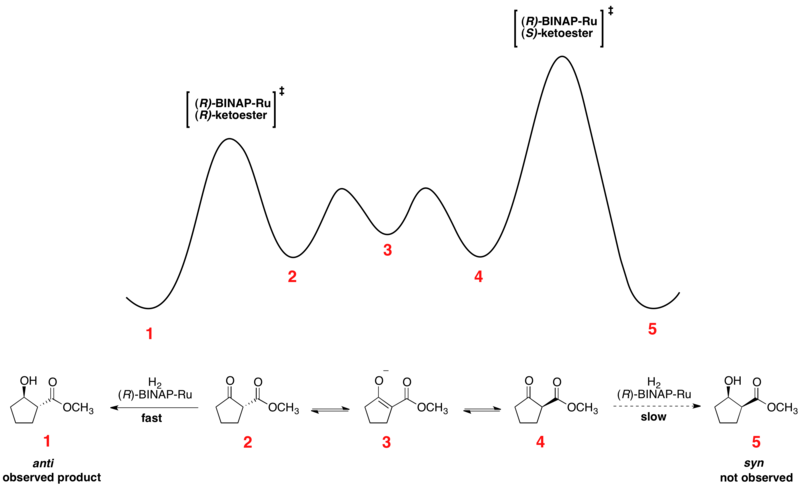
Los enantiómeros se interconvierten a través de su enol común , que es el mínimo energético ubicado entre los enantiómeros. La reacción mostrada produce una muestra con 93% de ee del producto anti mostrado arriba. La elección del solvente parece tener una influencia importante en la diastereoselectividad, ya que tanto el diclorometano como el metanol muestran efectividad para ciertos sustratos. Noyori y otros también han desarrollado catalizadores más nuevos que han mejorado tanto la ee como la relación diastereomérica (dr).

(S)-SINFO

Genêt y colaboradores desarrollaron SYNPHOS , un análogo de BINAP que forma complejos de rutenio, que realizan hidrogenaciones asimétricas altamente selectivas. [43] Se demostró que el Ru[SYNPHOS]Br 2 enantiopuro hidrogena selectivamente α-amino-β-cetoésteres racémicos a aminoalcoholes enantiopuros, como se muestra a continuación utilizando (R)-SYNPHOS. [44] Los 1,2- sin aminoalcoholes se prepararon a partir de compuestos amino protegidos con benzoilo , mientras que los productos anti se prepararon a partir de sales de clorhidrato de la amina.

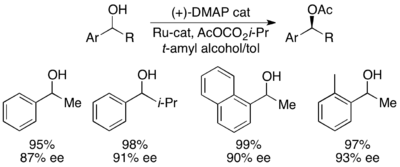
Modificación de la acilación de Fu

Catalizador de rutenio utilizado por Fu para la racemización de alcoholes secundarios

Recientemente, Gregory Fu y sus colegas informaron una modificación de su trabajo anterior de resolución cinética para producir una resolución cinética dinámica efectiva. [45] Utilizando el catalizador de racemización de rutenio que se muestra a la derecha y su catalizador DMAP quiral planar, Fu ha demostrado la resolución cinética dinámica de alcoholes secundarios con un rendimiento de hasta 99% y 93% ee, como se muestra a continuación. Se está trabajando para desarrollar aún más las aplicaciones del catalizador DMAP ampliamente utilizado para la resolución cinética dinámica.

Resoluciones cinéticas dinámicas enzimáticas

Se han reportado varias resoluciones cinéticas dinámicas enzimáticas. [46] Un excelente ejemplo que utiliza PSL resuelve eficazmente las aciloínas racémicas en presencia de trietilamina y acetato de vinilo como agente acilante. [47] Como se muestra a continuación, el producto se aisló con un rendimiento del 75 % y un 97 % de ee. Sin la presencia de la base, se produjo una resolución cinética regular, lo que resultó en un rendimiento del 45 % de producto acilado con >99 % de ee y un 53 % del material de partida con un 92 % de ee.

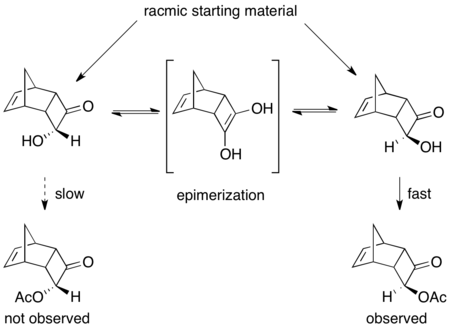
Otro ejemplo excelente, aunque no de alto rendimiento, es la resolución cinética de (±)-8-amino-5,6,7,8-tetrahidroquinolina. Cuando se expone a la lipasa B de Candida antarctica (CALB) en tolueno y acetato de etilo durante 3 a 24 horas, se produce una resolución cinética normal, lo que da como resultado un rendimiento del 45 % de 97 % ee de material de partida y un rendimiento del 45 % de producto de amina acilada con >97 % ee. Sin embargo, cuando se permite que la reacción se agite durante 40 a 48 horas, se recupera el material de partida racémico y >60 % del producto acilado con >95 % ee. [48]

Aquí, el material de partida que no reaccionó se racemiza in situ a través de una enamina dimérica, lo que da como resultado una recuperación de más del 50 % de rendimiento del producto de amina acilada enantiopura.

Resoluciones cinéticas dinámicas quimioenzimáticas

Se han descrito varios procedimientos que aprovechan un reactivo/catalizador químico para realizar la racemización del material de partida y una enzima para reaccionar selectivamente con un enantiómero, denominados resoluciones cinéticas dinámicas quimioenzimáticas. [49] Se utilizó PSL-C junto con un catalizador de rutenio (para la racemización) para producir δ-hidroxilactonas enantiopuras (>95 % ee). [50]

Catalizador de rutenio de Bäckvall para la racemización en la resolución cinética dinámica quimioenzimática de alcoholes secundarios

Más recientemente, Bäckvall ha resuelto alcoholes secundarios con rendimientos de hasta el 99 % y ee de hasta >99 % utilizando CALB y un complejo de racemización de rutenio. [51]

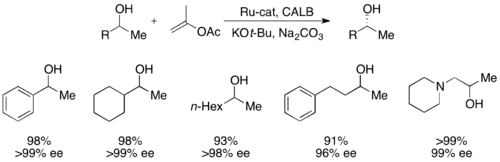
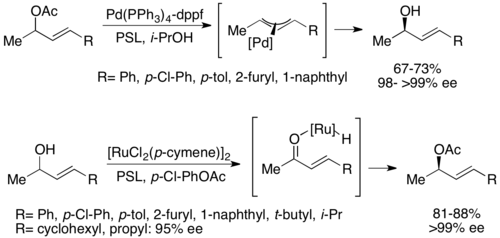
Un segundo tipo de resolución cinética dinámica quimioenzimática implica un complejo π-alílico de un acetato alílico con paladio . Aquí, la racemización ocurre con pérdida del acetato, formando un complejo catiónico con el centro del metal de transición, como se muestra a continuación. [52] Se ha demostrado que el paladio facilita esta reacción, mientras que se ha demostrado que el rutenio afecta una reacción similar, que también se muestra a continuación. [53]

Resolución cinética paralela

En la resolución cinética paralela (PKR), una mezcla racémica reacciona para formar dos productos no enantioméricos, a menudo a través de vías de reacción completamente diferentes. Con PKR, no hay compensación entre conversión y ee, ya que los productos formados no son enantiómeros. [54] [55] Una estrategia para PKR es eliminar el enantiómero menos reactivo (hacia el catalizador quiral deseado) de la mezcla de reacción sometiéndolo a un segundo conjunto de condiciones de reacción que reaccionan preferentemente con él, idealmente con una velocidad de reacción aproximadamente igual. Por lo tanto, ambos enantiómeros se consumen en diferentes vías a velocidades iguales. Los experimentos de PKR pueden ser estereodivergentes, regiodivergentes o estructuralmente divergentes. [56] Uno de los PKR más eficientes informados hasta la fecha fue logrado por Yoshito Kishi en 1998; la reducción CBS de una cetona esteroide racémica resultó en una reducción estereoselectiva, produciendo dos diastereómeros de >99% ee, como se muestra a continuación. [57]

La PKR también se ha logrado con el uso de catalizadores enzimáticos. Utilizando el hongo Mortierella isabellina NRRL 1757, la reducción de β-cetonitrilos racémicos proporciona dos diastereómeros, que pueden separarse y reoxidarse para dar β-cetonitrilos altamente enantiopuros. [58] Sin embargo, todavía no se han descubierto resoluciones cinéticas paralelas altamente útiles para la síntesis. Se han descubierto varios procedimientos que dan ee y rendimientos aceptables, pero hay muy pocos ejemplos que den una resolución cinética paralela altamente selectiva y no simplemente reacciones algo selectivas. Por ejemplo, la resolución cinética paralela de Fu de 4-alquinales produce ciclobutanona muy enantioenriquecida con bajo rendimiento y ciclopentenona ligeramente enantioenriquecida, como se muestra a continuación. [59]

En teoría, la resolución cinética paralela puede dar los valores más altos de ee de los productos, ya que solo un enantiómero da cada producto deseado. Por ejemplo, para dos reacciones complementarias, ambas con s = 49, una conversión del 100 % daría productos con un rendimiento del 50 % y un ee del 96 %. Estos mismos valores requerirían s = 200 para una resolución cinética simple. Como tal, la promesa de PKR continúa atrayendo mucha atención. La reducción CBS de Kishi sigue siendo uno de los pocos ejemplos que cumplen esta promesa.

Véase también

Referencias

  1. ^ Fiaud, JC; Kagan, HB (1988). "Resolución cinética". En Eliel, EL; Wilen, SH (eds.). Temas de estereoquímica . Vol. 18. Nueva York: John Wiley and Sons, Inc., págs. 249–340.
  2. ^ Robinson, DEJE; Bull, SD (2005). "Estrategias de resolución cinética utilizando catalizadores no enzimáticos". Tetrahedron: Asymmetry . 14 (11): 1407–1446. doi :10.1016/S0957-4166(03)00209-X.
  3. ^ Pasteur, LC (1858). "Mémoire sur la fermentation de l'acide tartrique". CR Acad. Ciencia. París . 46 : 615–618.
  4. ^ Marckwald, W.; McKenzie, A. (1899). "Ueber eine principiell neue Methode zur Spaltung racemischer Verbindungen in die activen Bestandtheile". Ber. Alemán. Química. Ges . 32 (2): 2130–2136. doi :10.1002/cber.189903202130.
  5. ^ Roger, R.; Read, J. (1952). "Alexander McKenzie: 1869-1951". Esquelas de miembros de la Royal Society . 8 (21): 206–228. doi : 10.1098/rsbm.1952.0014 .
  6. ^ ab Keith, JM; Larrow, JF; Jacobsen, EN (2001). "Consideraciones prácticas en reacciones de resolución cinética". Adv. Synth. Catal . 343 : 5–26. doi :10.1002/1615-4169(20010129)343:1<5::AID-ADSC5>3.0.CO;2-I.
  7. ^ Wurz, RP; Lee, EC; Ruble, JC; Fu, GC (2007). "Síntesis y resolución de derivados quirales planos de 4-(dimetilamino)piridina". Adv. Synth. Catal . 349 (14–15): 2345–2352. doi :10.1002/adsc.200700219.
  8. ^ Ruble, JC; Latham, HA; Fu, GC (1997). "Resolución cinética efectiva de alcoholes secundarios con un análogo planar-quiral de 4-(dimetilamino)piridina. Uso del grupo Fe(C 5 Ph 5 ) en catálisis asimétrica". J. Am. Chem. Soc . 119 (6): 1492–1493. doi :10.1021/ja963835b.
  9. ^ Ruble, JC; Tweddell, J.; Fu, GC (1998). "Resolución cinética de arilalquilcarbinoles catalizada por un derivado planar-quiral de DMAP: un nuevo parámetro de referencia para la acilación no enzimática". J. Org. Chem . 63 (9): 2794–2795. doi :10.1021/jo980183w.
  10. ^ Tao, B.; Ruble, JC; Hoic, DA; Fu, GC (1999). "Resolución cinética no enzimática de alcoholes propargílicos mediante un derivado DMAP planar-quiral: caracterización cristalográfica del catalizador acilado". J. Am. Chem. Soc . 121 (21): 2091–5092. doi :10.1021/ja9906958.
  11. ^ Bellemin-Laponnaz, S.; Tweddell, J.; Ruble, JC; Breitling, FM; Fu, GC (2000). "La resolución cinética de alcoholes alílicos mediante un catalizador de acilación no enzimático; aplicación a la síntesis de productos naturales". Chem. Commun. (12): 2091–5092. doi :10.1039/B002041I.
  12. ^ Arai, S.; Bellemin-Laponnaz, S.; Fu, GC (2001). "Resolución cinética de aminas mediante un catalizador de acilación no enzimático". Angew. Chem. Int. Ed . 133 (1): 240–242. doi :10.1002/1521-3757(20010105)113:1<240::AID-ANGE240>3.0.CO;2-E.
  13. ^ Arp, FO; Fu, GC (2006). "Resoluciones cinéticas de inolinas mediante un catalizador de acilación no enzimático". J. Am. Chem. Soc . 128 (44): 14264–14265. doi :10.1021/ja0657859. PMC 2569996. PMID  17076493 . 
  14. ^ Katsuki, T.; Sharpless, KB (1980). "El primer método práctico para la epoxidación asimétrica". J. Am. Chem. Soc . 102 (18): 5974–5976. doi :10.1021/ja00538a077.
  15. ^ Martin, V.; Woodard, S.; Katsuki, T.; Yamada, Y.; Ikeda, M.; Sharpless, KB (1981). "Resolución cinética de alcoholes alílicos racémicos mediante epoxidación enantioselectiva. ¿Una ruta hacia sustancias de pureza enantiomérica absoluta?". J. Am. Chem. Soc . 103 (23): 6237–6240. doi :10.1021/ja00410a053.
  16. ^ Gao, Yun; Klunder, JM; Hanson, RM; Masamune, H.; Ko, SY; Sharpless, KB (1987). "Epoxidación catalítica asimétrica y resolución cinética: procedimientos modificados que incluyen derivatización in situ". J. Am. Chem. Soc . 109 (19): 5765–5780. doi :10.1021/ja00253a032.
  17. ^ Kitano, Y.; Matsumoto, T.; Sato, F. (1988). "Una resolución cinética altamente eficiente de alcoholes alílicos secundarios γ- y β- trimetilsilil mediante la epoxidación asimétrica sin distorsión". Tetrahedron . 44 (13): 4073–4086. doi :10.1016/S0040-4020(01)86657-6.
  18. ^ VanNieuwenhze, MS; Sharpless, KB (1993). "Resolución cinética de olefinas racémicas mediante dihidroxilación asimétrica". J. Am. Chem. Soc . 115 (17): 7864–7865. doi :10.1021/ja00070a037.
  19. ^ Corey, EJ; Noe, MC; Guzman-Perez, A. (1995). "Resolución cinética por dihidroxilación enantioselectiva de ésteres alílicos secundarios de 4-metoxibenzoato utilizando un catalizador de alcaloide de cinchona diseñado mecánicamente". J. Am. Chem. Soc . 117 (44): 10817–10824. doi :10.1021/ja00149a004.
  20. ^ Lorenz, JC; Frohn, M.; Zhou, X.; Zhang, J.-R.; Tang, Y.; Burke, C.; Shi, Y. (2005). "Estudios de estados de transición sobre la epoxidación asimétrica mediada por dioxirano mediante resolución cinética y desimetrización". J. Org. Chem . 70 (8): 2904–2911. doi :10.1021/jo048217p. PMID  15822948.
  21. ^ Larrow, JF; Schaus, SE; Jacobsen, EN (1996). "Resolución cinética de epóxidos terminales mediante apertura de anillo altamente regioselectiva y enantioselectiva con TMSN3. Una ruta catalítica eficiente para 1,2-aminoalcoholes". J. Am. Chem. Soc . 118 (31): 7420–7421. doi :10.1021/ja961708+.
  22. ^ Tokunaga, M.; Larrow, JF; Kakiuchi, F.; Jacobsen, EN (1997). "Catálisis asimétrica con agua: resolución cinética eficiente de epóxidos terminales mediante hidrólisis catalítica". Science . 277 (5328): 936–938. doi :10.1126/science.277.5328.936. PMID  9252321.
  23. ^ Brandes, BD; Jacobsen, EN (1997). "Síntesis de óxido de 3-cloroestireno enantiopuro mediante una secuencia de resolución cinética de epoxidación-hidrolítica asimétrica". Tet. Asymm . 8 (23): 3927–3933. doi :10.1016/S0957-4166(97)00568-5.
  24. ^ Sudalai, A.; Karabal, PU; Devalankar, DA (2013). "γ-butirolactonas ópticamente puras y ésteres epoxi a través de dos HKR estereocentrados de ésteres epoxi 3-sustituidos: una síntesis formal de (−)-paroxetina, Ro 67-8867 y (+)-eldanolida". Org. Biomol. Química . 11 (8): 1280–1285. doi :10.1039/c3ob27321k. PMID  23334653.
  25. ^ Hashiguchi, S.; Fujii, A.; Haack, K.-J.; Matsumura, K.; Ikariya, T.; Noyori, R. (1997). "Resolución cinética de alcoholes secundarios racémicos mediante transferencia de hidrógeno catalizada por RuII". Angew. Chem. Int. Ed . 36 (3): 288–290. doi :10.1002/anie.199702881.
  26. ^ Hashiguchi, S.; Fujii, A.; Takehara, J.; Ikariya, T.; Noyori, R. (1995). "Hidrogenación por transferencia asimétrica de cetonas aromáticas catalizada por complejos quirales de rutenio(II)". J. Am. Chem. Soc . 117 (28): 7562–7563. doi :10.1021/ja00133a037.
  27. ^ Nishibayashi, Y.; Takei, I.; Uemura, S.; Hidai, M. (1999). "Reacción redox enantioselectiva extremadamente alta de cetonas y alcoholes catalizada por RuCl2(PPh3)(oxazolinilferrocenilfosfina)". Organometallics . 18 (12): 2291–2293. doi :10.1021/om990210o.
  28. ^ Kitamura, M.; Kasahara, I.; Manabe, K.; Noyori, R.; Takaya, H. (1988). "Resolución cinética de alcoholes alílicos racémicos mediante hidrogenación catalizada por BINAP-rutenio(II)". J. Org. Chem . 53 (3): 708–710. doi :10.1021/jo00238a048.
  29. ^ Hoveyda, AH; Schrock, RR (2001). "Metátesis catalítica asimétrica de olefinas". Chem. Eur. J. 7 ( 5): 945–950. doi :10.1002/1521-3765(20010302)7:5<945::AID-CHEM945>3.0.CO;2-3. PMID  11303874.
  30. ^ Patente estadounidense 6656710, Bommarius & Verseck, "Proceso para la producción de aminoácidos utilizando racemasa y acilato", asignada a Degussa AG 
  31. ^ Ghanem, A.; Aboul-Enein, HY (2005). "Aplicación de lipasas en la resolución cinética de racematos". Quiralidad . 17 (1): 1–15. doi :10.1002/chir.20089. PMID  15515046.
  32. ^ "Tecnología quiral: biocatálisis industrial con enzimas hidrolíticas estándar". Revista de productos químicos especializados . 27 (8): 38. 2007.
  33. ^ Ghanem, A.; Schurig, V. (2003). "Transesterificación irreversible catalizada por lipasa de alcoholes secundarios utilizando acetato de isopropenilo" (PDF) . Monatshefte für Chemie . 134 (8): 1151-1157. doi :10.1007/s00706-003-0025-1. S2CID  96922176.
  34. ^ Santaniello, E.; Ferraboschi, P.; Grisenti, P.; Manzocchi, A. (1992). "El enfoque biocatalítico para la preparación de bloques de construcción quirales enantioméricamente puros". Chem . Rev. 92 (5): 1071–1140. doi :10.1021/cr00013a016.
  35. ^ Ticozzi, C.; Zanarotti, Antonio (1989). "Reducción microbiana enantioselectiva de 5-acetilisoxazolinas: un nuevo método para el control estereoquímico de la reducción en levaduras". Liebigs Ann. Chem . 1989 (12): 1257–1259. doi :10.1002/jlac.198919890299.
  36. ^ Fantin, G.; Fogagnolo, M.; Medici, A.; Pedrini, P.; Poli, S. (1993). "Resolución cinética de etanoles 1-aril- y 1-heteroaril mediante oxidación con levadura de panadería". Tetrahedron Lett . 34 (5): 883–884. doi :10.1016/0040-4039(93)89039-S. hdl :11392/462444.
  37. ^ Brooks, DW; Wilson, M.; Webb, M. (1987). "Diferentes reacciones enzimáticas de un par enantiomérico: resolución cinética dual simultánea de un éster ceto por levadura de panadería". J. Org. Chem . 52 (11): 2244–2248. doi :10.1021/jo00387a026.
  38. ^ Pellissier, H. (2008). "Desarrollos recientes en resolución cinética dinámica". Tetrahedron . 64 (8): 1563–1601. doi :10.1016/j.tet.2007.10.080.
  39. ^ Pellissier, H. (2003). "Resolución cinética dinámica". Tetrahedron . 59 (42): 8291–8327. doi :10.1016/S0040-4020(03)01022-6.
  40. ^ Ward, RS (1995). "Resolución cinética dinámica". Tetrahedron: Asymmetry . 6 (7): 1475–1490. doi :10.1016/0957-4166(95)00179-S.
  41. ^ Kitamura, M.; Tokunaga, M.; Noyori, R. (1993). "Expresión cuantitativa de la resolución cinética dinámica de enantiómeros quirales lábiles: hidrogenación estereoselectiva de ésteres carboxílicos 3-oxo sustituidos en 2 catalizados por complejos BINAP-rutenio(II)". J. Am. Chem. Soc . 115 (1): 144–152. doi :10.1021/ja00054a020.
  42. ^ Noyori, R.; Ikeda, T.; Ohkuma, T.; Widhalm, M.; Kitamura, M.; Takaya, H.; Akutagawa, S.; Sayo, N.; Saito, T. (1989). "Hidrogenación estereoselectiva mediante resolución cinética dinámica". J. Am. Chem. Soc . 111 (25): 9134–9135. doi :10.1021/ja00207a038.
  43. ^ de Paule, SD; Jeulin, S.; Ratovelomanana-Vidal, V.; Genêt, JP.; Champion, N.; Dellis, P. (2003). "Estudios de síntesis y modelado molecular de SYNPHOS®, un nuevo y eficiente ligando de difosfano para la hidrogenación asimétrica catalizada por rutenio". Eur. J. Org. Chem . 2003 (10): 1931–1941. doi :10.1002/ejoc.200200634.
  44. ^ Mordant, C.; Ratovelomanana-Vidal, V.; Dünkelmann, P.; Genêt, J.-P. (2004). "Una ruta versátil para sintetizar y anti-α-amino β-hidroxiésteres a partir de β-cetoésteres mediante resolución cinética dinámica con el catalizador Ru-SYNPHOS®". Eur. J. Org. Chem . 2004 (14): 3017–3026. doi :10.1002/ejoc.200400078.
  45. ^ Lee, SY; Murphy, JM; Ukai, A.; Fu, GC (2012). "Resolución cinética dinámica no enzimática de alcoholes secundarios mediante acilación enantioselectiva: estudios sintéticos y mecanísticos". J. Am. Chem. Soc . 134 (36): 15149–15153. doi :10.1021/ja307425g. PMC 3447740. PMID  22934603 . 
  46. ^ Pellissier, H. (2003). "Transesterificación dinámica mediada por lipasa y trietilamina de una aciloína tricíclica con una mesoestructura latente: una nueva ruta hacia el oxodiciclopentadieno ópticamente puro". Tetrahedron . 59 (42): 8291–9327. doi :10.1016/S0040-4020(03)01022-6.
  47. ^ Taniguchi, T.; Ogasawara, K. (1997). "Transesterificación dinámica mediada por lipasa y trietilamina de una aciloína tricíclica con una mesoestructura latente: una nueva ruta para obtener oxodiciclopentadieno ópticamente puro". Chemical Communications (15): 1399–1400. doi :10.1039/A702910A.
  48. ^ Crawford, JB; Skerlj, RT; Bridger, GJ (2007). "Resolución cinética dinámica espontánea mediada enzimáticamente de 8-amino-5,6,7,8-tetrahidroquinolina". J. Org. Chem . 72 (2): 669–671. doi :10.1021/jo062037t. PMID  17221995.
  49. ^ Pàmies, O.; Bäckvall, J.-E. (2004). "Resolución cinética dinámica quimioenzimática". Tendencias en biotecnología . 22 (3): 130–135. doi :10.1016/j.tibtech.2004.01.005. PMID  15036863.
  50. ^ Pàmies, O.; Bäckvall, J.-E. (2002). "Resolución cinética enzimática y resolución cinética dinámica quimioenzimática de δ-hidroxiésteres. Una ruta eficiente para las δ-lactonas quirales". J. Org. Chem . 67 (4): 1261–1265. doi :10.1021/jo016096c. PMID  11846671.
  51. ^ Martín-Matute, B.; Edin, M.; Bogár, K.; Kaynak, FB; Bäckvall, J.-E. (2005). "Catálisis combinada de rutenio(II) y lipasa para una resolución cinética dinámica eficiente de alcoholes secundarios. Una perspectiva del mecanismo de racemización". J. Am. Chem. Soc . 127 (64): 8817–8825. doi :10.1021/ja051576x. PMID  15954789.
  52. ^ Choi, YK; Suh, JH; Lee, D.; Lim, IT; Jung, JY; Kim, M.-J. (1999). "Resolución cinética dinámica de acetatos alílicos acíclicos utilizando lipasa y paladio". J. Org. Chem . 64 (22): 8423–8424. doi :10.1021/jo990956w. PMID  11674772.
  53. ^ Lee, D.; Huh, EA; Kim, M.-J.; Jung, HM; Koh, JH; Park, J. (2000). "Resolución cinética dinámica de alcoholes alílicos mediada por catalizadores basados ​​en rutenio y lipasa". Org. Lett . 2 (15): 2377–2379. doi :10.1021/ol006159y. PMID  10930288.
  54. ^ Eames, J. (2000). "Resoluciones cinéticas paralelas". Angew. Chem. Int. Ed . 39 (5): 885–888. doi :10.1002/(SICI)1521-3773(20000303)39:5<885::AID-ANIE885>3.0.CO;2-2. PMID  10760881.
  55. ^ Dehil, JR; Gotor, V. (2002). "Resolución cinética paralela de mezclas racémicas: ¿una nueva estrategia para la preparación de compuestos enantiopuros?". Chem. Soc. Rev. 31 ( 6): 365–370. doi :10.1039/B205280F. PMID  12491751.
  56. ^ Vedejs, E.; Jure, M. (2005). "Eficiencia en la resolución cinética no enzimática". Angew. Chem. Int. Ed . 44 (5): 3974–4001. doi :10.1002/anie.200460842. PMID  15942973.
  57. ^ Kurosu, M.; Kishi, Y. (1998). "Un nuevo ejemplo de resolución óptica de cetonas racémicas originadas a partir de la síntesis de batracotoxina". J. Org. Chem . 63 (18): 6100–6101. doi :10.1021/jo981416m. PMID  11672234.
  58. ^ Dehil, JR; Gotor, V. (2002). "Preparación de cetonas y alcoholes enantiopuros que contienen un estereocentro cuaternario mediante resolución cinética paralela de β-cetonitrilos". J. Org. Chem . 67 (5): 1716–1718. doi :10.1021/jo011092t. PMID  11871913.
  59. ^ Tanaka, K.; Fu, GC (2003). "Resolución cinética paralela de 4-alquinales catalizada por Rh(I)/Tol-BINAP: síntesis de ciclobutanonas y ciclopentenonas enantioenriquecidas". J. Am. Chem. Soc . 125 (27): 8078–8079. doi :10.1021/ja035489l. PMID  12837058.

Lectura adicional

  • Resoluciones cinéticas dinámicas. Reunión del grupo MacMillan. Jake Wiener Link
  • Resolución cinética dinámica: un enfoque eficaz para la síntesis asimétrica. Reunión del supergrupo de Erik Alexanian del 30 de marzo de 2005 Enlace
  • Resolución cinética dinámica: aplicaciones prácticas en síntesis. Seminario de tercer año de Valerie Keller 1 de noviembre de 2001 Enlace
  • Resolución cinética. Seminario de literatura del grupo David Ebner Stoltz. 4 de junio de 2003. Enlace
  • Resoluciones cinéticas. Presentación de UT Southwestern. Enlace
Retrieved from "https://en.wikipedia.org/w/index.php?title=Kinetic_resolution&oldid=1237581484"