Ecuación de Arrhenius
Fórmula para la dependencia de la temperatura de las velocidades de las reacciones químicas

En química física , la ecuación de Arrhenius es una fórmula para la dependencia de la temperatura de las velocidades de reacción . La ecuación fue propuesta por Svante Arrhenius en 1889, basada en el trabajo del químico holandés Jacobus Henricus van 't Hoff , quien había notado en 1884 que la ecuación de van 't Hoff para la dependencia de la temperatura de las constantes de equilibrio sugiere una fórmula de este tipo para las velocidades de reacciones tanto directas como inversas. Esta ecuación tiene una aplicación vasta e importante en la determinación de la velocidad de las reacciones químicas y para el cálculo de la energía de activación . Arrhenius proporcionó una justificación física e interpretación para la fórmula. [1] [2] [3] [4] Actualmente, se ve mejor como una relación empírica . [5] : 188  Se puede utilizar para modelar la variación de temperatura de los coeficientes de difusión , la población de vacantes de cristales , las velocidades de fluencia y muchos otros procesos y reacciones inducidos térmicamente. La ecuación de Eyring , desarrollada en 1935, también expresa la relación entre la velocidad y la energía.

Ecuación

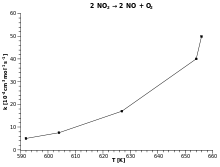
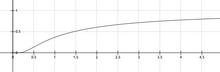
En casi todos los casos prácticos, y k aumenta rápidamente con T . mi a ≫ R yo {\displaystyle E_{a}\gg RT}
Matemáticamente, a temperaturas muy altas tales que , k se estabiliza y se aproxima a A como límite, pero este caso no ocurre en condiciones prácticas. mi a ≪ R yo {\displaystyle E_{a}\ll RT}

La ecuación de Arrhenius describe la dependencia exponencial de la constante de velocidad de una reacción química con respecto a la temperatura absoluta como donde a = A mi − mi a R yo , {\displaystyle k=Ae^{\frac {-E_{\text{a}}}{RT}},}

Alternativamente, la ecuación puede expresarse como donde k = A e − E a k B T , {\displaystyle k=Ae^{\frac {-E_{\text{a}}}{k_{\text{B}}T}},}

La única diferencia es la unidad de E a : la primera forma utiliza energía por mol , que es común en química, mientras que la segunda forma utiliza energía por molécula directamente, que es común en física. Las diferentes unidades se tienen en cuenta al utilizar la constante de los gases , R , o la constante de Boltzmann , k B , como multiplicador de la temperatura T .

La unidad del factor preexponencial A es idéntica a la de la constante de velocidad y variará dependiendo del orden de la reacción. Si la reacción es de primer orden, tiene la unidad s −1 , y por esa razón a menudo se le llama factor de frecuencia o frecuencia de intento de la reacción. De manera más simple, k es el número de colisiones que resultan en una reacción por segundo, A es el número de colisiones (que conducen a una reacción o no) por segundo que ocurren con la orientación adecuada para reaccionar [7] y es la probabilidad de que cualquier colisión dada resulte en una reacción. Se puede ver que ya sea aumentar la temperatura o disminuir la energía de activación (por ejemplo, mediante el uso de catalizadores ) resultará en un aumento en la velocidad de reacción. e − E a R T {\displaystyle e^{\frac {-E_{\text{a}}}{RT}}}

Dado el pequeño rango de temperatura de los estudios cinéticos, es razonable aproximar la energía de activación como independiente de la temperatura. De manera similar, bajo un amplio rango de condiciones prácticas, la débil dependencia de la temperatura del factor preexponencial es insignificante en comparación con la dependencia de la temperatura del factor ⁠ ⁠ e − E a R T {\displaystyle e^{\frac {-E_{\text{a}}}{RT}}} ; excepto en el caso de reacciones limitadas por difusión "sin barreras" , en cuyo caso el factor preexponencial es dominante y es directamente observable.

Con esta ecuación se puede estimar aproximadamente que la velocidad de reacción aumenta en un factor de aproximadamente 2 a 3 por cada 10 °C de aumento de temperatura, para valores comunes de energía de activación y rango de temperatura. [8]

El factor denota la fracción de moléculas con energía mayor o igual a . [9] e − E a R T {\displaystyle e^{\frac {-E_{a}}{RT}}} E a {\displaystyle E_{a}}

Derivación

Van't Hoff argumentó que la temperatura de una reacción y la constante de equilibrio estándar exhiben la relación: T {\displaystyle T} k e 0 {\displaystyle k_{\text{e}}^{0}}

d ln ⁡ k e 0 d T = Δ U 0 R T 2 {\displaystyle {\frac {d\ln k_{\text{e}}^{0}}{dT}}={\frac {\Delta U^{0}}{RT^{2}}}} ( 1 )

donde denota el valor de cambio de energía interna estándar apropiado . Δ U 0 {\displaystyle \Delta U^{0}}

Sean y respectivamente las velocidades de reacción hacia adelante y hacia atrás de la reacción de interés, luego ⁠ ⁠ , [10] una ecuación de la cual se sigue naturalmente. k f {\displaystyle k_{\text{f}}} k b {\displaystyle k_{\text{b}}} k e 0 = k f k b {\displaystyle k_{\text{e}}^{0}={\frac {k_{\text{f}}}{k_{\text{b}}}}} ln ⁡ k e 0 = ln ⁡ k f − ln ⁡ k b {\displaystyle \ln k_{\text{e}}^{0}=\ln k_{\text{f}}-\ln k_{\text{b}}}

Sustituyendo la expresión en la ecuación ( 1 ), obtenemos ⁠ ⁠ . ln ⁡ k e 0 {\displaystyle \ln k_{\text{e}}^{0}} d ln ⁡ k f d T − d ln ⁡ k b d T = Δ U 0 R T 2 {\displaystyle {\frac {d\ln k_{\text{f}}}{dT}}-{\frac {d\ln k_{\text{b}}}{dT}}={\frac {\Delta U^{0}}{RT^{2}}}}

La ecuación anterior se puede descomponer en las dos ecuaciones siguientes:

d ln ⁡ k f d T = constant + E f R T 2 {\displaystyle {\frac {d\ln k_{\text{f}}}{dT}}={\text{constant}}+{\frac {E_{\text{f}}}{RT^{2}}}} ( 2 )

y

d ln ⁡ k b d T = constant + E b R T 2 {\displaystyle {\frac {d\ln k_{\text{b}}}{dT}}={\text{constant}}+{\frac {E_{\text{b}}}{RT^{2}}}} ( 3 )

donde y son las energías de activación asociadas con las reacciones hacia adelante y hacia atrás respectivamente, con . E f {\displaystyle E_{\text{f}}} E b {\displaystyle E_{\text{b}}} Δ U 0 = E f − E b {\displaystyle \Delta U^{0}=E_{\text{f}}-E_{\text{b}}}

Los hallazgos experimentales sugieren que las constantes en las ecuaciones ( 2 ) y ( 3 ) pueden tratarse como iguales a cero, de modo que

d ln ⁡ k f d T = E f R T 2 {\displaystyle {\frac {d\ln k_{\text{f}}}{dT}}={\frac {E_{\text{f}}}{RT^{2}}}} ()

y

d ln ⁡ k b d T = E b R T 2 {\displaystyle {\frac {d\ln k_{\text{b}}}{dT}}={\frac {E_{\text{b}}}{RT^{2}}}} ()

Integrando estas ecuaciones y tomando el exponencial se obtienen los resultados ⁠ ⁠ k f = A f e − E f / R T {\displaystyle k_{\text{f}}=A_{\text{f}}e^{-E_{\text{f}}/RT}} y ⁠ ⁠ k b = A b e − E b / R T {\displaystyle k_{\text{b}}=A_{\text{b}}e^{-E_{\text{b}}/RT}} , donde cada factor preexponencial o es matemáticamente el exponencial de la constante de integración para la respectiva integral indefinida en cuestión. [11] A f {\displaystyle A_{\text{f}}} A b {\displaystyle A_{\text{b}}}

El complot de Arrhenius

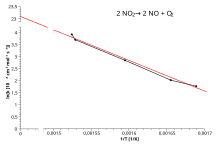
Gráfica lineal de Arrhenius: ln  k contra 1/ T .

Tomando el logaritmo natural de la ecuación de Arrhenius se obtiene: ln ⁡ k = ln ⁡ A − E a R 1 T . {\displaystyle \ln k=\ln A-{\frac {E_{\text{a}}}{R}}{\frac {1}{T}}.}

Reordenando los rendimientos: ln ⁡ k = − E a R ( 1 T ) + ln ⁡ A . {\displaystyle \ln k={\frac {-E_{\text{a}}}{R}}\left({\frac {1}{T}}\right)+\ln A.}

Esto tiene la misma forma que una ecuación para una línea recta: donde x es el recíproco de T . y = a x + b , {\displaystyle y=ax+b,}

Por lo tanto, cuando una reacción tiene una constante de velocidad que obedece a la ecuación de Arrhenius, una gráfica de ln  k en función de T −1 da una línea recta, cuya pendiente e intersección se pueden utilizar para determinar E a y A respectivamente. Este procedimiento es común en la cinética química experimental. La energía de activación se obtiene simplemente multiplicando por (− R ) la pendiente de la línea recta dibujada a partir de una gráfica de ln  k en función de (1/ T ): E a ≡ − R [ ∂ ln ⁡ k ∂ ( 1 / T ) ] P . {\displaystyle E_{\text{a}}\equiv -R\left[{\frac {\partial \ln k}{\partial (1/T)}}\right]_{P}.}

Ecuación de Arrhenius modificada

La ecuación de Arrhenius modificada [12] hace explícita la dependencia de la temperatura del factor preexponencial. La ecuación modificada suele tener la forma k = A T n e − E a R T . {\displaystyle k=AT^{n}e^{\frac {-E_{\text{a}}}{RT}}.}

La expresión original de Arrhenius anterior corresponde a n = 0. Las constantes de velocidad ajustadas se encuentran típicamente en el rango −1 < n < 1. Los análisis teóricos producen varias predicciones para n . Se ha señalado que "no es factible establecer, sobre la base de estudios de temperatura de la constante de velocidad, si la dependencia T 1/2 predicha del factor preexponencial se observa experimentalmente". [5] : 190  Sin embargo, si hay evidencia adicional disponible, de la teoría y/o del experimento (como la dependencia de la densidad), no hay obstáculo para pruebas incisivas de la ley de Arrhenius.

Otra modificación común es la forma exponencial estirada [ cita requerida ] donde β es un número adimensional de orden 1. Esto generalmente se considera como una corrección puramente empírica o un factor de ajuste para hacer que el modelo se ajuste a los datos, pero puede tener un significado teórico, por ejemplo, mostrando la presencia de un rango de energías de activación o en casos especiales como el salto de rango de la variable Mott . k = A exp ⁡ [ − ( E a R T ) β ] , {\displaystyle k=A\exp \left[-\left({\frac {E_{a}}{RT}}\right)^{\beta }\right],}

Interpretación teórica de la ecuación

El concepto de energía de activación de Arrhenius

Arrhenius argumentó que para que los reactivos se transformen en productos, primero deben adquirir una cantidad mínima de energía, llamada energía de activación E a . A una temperatura absoluta T , la fracción de moléculas que tienen una energía cinética mayor que E a se puede calcular a partir de la mecánica estadística . El concepto de energía de activación explica la naturaleza exponencial de la relación y, de una forma u otra, está presente en todas las teorías cinéticas.

Los cálculos de las constantes de velocidad de reacción implican un promedio de energía sobre una distribución de Maxwell-Boltzmann con un límite inferior y, por lo tanto, a menudo son del tipo de funciones gamma incompletas , que resultan ser proporcionales a . E a {\displaystyle E_{\text{a}}} e − E a R T {\displaystyle e^{\frac {-E_{\text{a}}}{RT}}}

Teoría de colisiones

Un enfoque es la teoría de colisión de las reacciones químicas, desarrollada por Max Trautz y William Lewis en los años 1916-18. En esta teoría, se supone que las moléculas reaccionan si chocan con una energía cinética relativa a lo largo de su línea de centros que excede E a . Se encuentra que el número de colisiones binarias entre dos moléculas diferentes por segundo por unidad de volumen es [13] donde N A es la constante de Avogadro , d AB es el diámetro promedio de A y B , T es la temperatura que se multiplica por la constante de Boltzmann k B para convertirla en energía, y μ AB es la masa reducida . z A B = N A d A B 2 8 π k B T μ A B , {\displaystyle z_{AB}=N_{\text{A}}d_{AB}^{2}{\sqrt {\frac {8\pi k_{\text{B}}T}{\mu _{AB}}}},}

La constante de velocidad se calcula entonces como ⁠ ⁠ k = z A B e − E a R T {\displaystyle k=z_{AB}e^{\frac {-E_{\text{a}}}{RT}}} , de modo que la teoría de colisiones predice que el factor preexponencial es igual al número de colisiones z AB . Sin embargo, para muchas reacciones esto no concuerda bien con el experimento, por lo que la constante de velocidad se escribe en cambio como ⁠ ⁠ k = ρ z A B e − E a R T {\displaystyle k=\rho z_{AB}e^{\frac {-E_{\text{a}}}{RT}}} . Aquí hay un factor estérico empírico , a menudo mucho menor que 1,00, que se interpreta como la fracción de colisiones suficientemente energéticas en las que las dos moléculas tienen la orientación mutua correcta para reaccionar. [13] ρ {\displaystyle \rho }

Teoría del estado de transición

La ecuación de Eyring , otra expresión similar a la de Arrhenius, aparece en la " teoría de estados de transición " de las reacciones químicas, formulada por Eugene Wigner , Henry Eyring , Michael Polanyi y MG Evans en la década de 1930. La ecuación de Eyring puede escribirse: donde es la energía de activación de Gibbs, es la entropía de activación , es la entalpía de activación, es la constante de Boltzmann y es la constante de Planck . [14] k = k B T h e − Δ G ‡ R T = k B T h e Δ S ‡ R e − Δ H ‡ R T , {\displaystyle k={\frac {k_{\text{B}}T}{h}}e^{-{\frac {\Delta G^{\ddagger }}{RT}}}={\frac {k_{\text{B}}T}{h}}e^{\frac {\Delta S^{\ddagger }}{R}}e^{-{\frac {\Delta H^{\ddagger }}{RT}}},} Δ G ‡ {\displaystyle \Delta G^{\ddagger }} Δ S ‡ {\displaystyle \Delta S^{\ddagger }} Δ H ‡ {\displaystyle \Delta H^{\ddagger }} k B {\displaystyle k_{\text{B}}} h {\displaystyle h}

A primera vista, esto parece una exponencial multiplicada por un factor que es lineal en temperatura. Sin embargo, la energía libre es en sí misma una cantidad dependiente de la temperatura. La energía libre de activación es la diferencia de un término de entalpía y un término de entropía multiplicado por la temperatura absoluta. El factor preexponencial depende principalmente de la entropía de activación. La expresión general toma nuevamente la forma de una exponencial de Arrhenius (de entalpía en lugar de energía) multiplicada por una función de variación lenta de T . La forma precisa de la dependencia de la temperatura depende de la reacción y se puede calcular utilizando fórmulas de mecánica estadística que involucran las funciones de partición de los reactivos y del complejo activado. Δ G ‡ = Δ H ‡ − T Δ S ‡ {\displaystyle \Delta G^{\ddagger }=\Delta H^{\ddagger }-T\Delta S^{\ddagger }}

Limitaciones de la idea de la energía de activación de Arrhenius

Tanto la energía de activación de Arrhenius como la constante de velocidad k se determinan experimentalmente y representan parámetros macroscópicos específicos de la reacción que no están simplemente relacionados con las energías umbral y el éxito de las colisiones individuales a nivel molecular. Consideremos una colisión particular (una reacción elemental) entre las moléculas A y B. El ángulo de colisión, la energía de traslación relativa, la energía interna (particularmente vibracional) determinarán la probabilidad de que la colisión produzca una molécula de producto AB. Las mediciones macroscópicas de E y k son el resultado de muchas colisiones individuales con diferentes parámetros de colisión. Para investigar las velocidades de reacción a nivel molecular, se realizan experimentos en condiciones cercanas a la colisión y este tema a menudo se denomina dinámica de reacción molecular. [15]

Otra situación en la que la explicación de los parámetros de la ecuación de Arrhenius no es suficiente es en la catálisis heterogénea , especialmente para las reacciones que muestran una cinética de Langmuir-Hinshelwood . Claramente, las moléculas en las superficies no "chocan" directamente, y una simple sección transversal molecular no se aplica aquí. En cambio, el factor preexponencial refleja el recorrido a través de la superficie hacia el sitio activo. [16]

Existen desviaciones de la ley de Arrhenius durante la transición vítrea en todas las clases de materia formadora de vidrio. [17] La ​​ley de Arrhenius predice que el movimiento de las unidades estructurales (átomos, moléculas, iones, etc.) debería desacelerarse a un ritmo más lento a través de la transición vítrea de lo que se observa experimentalmente. En otras palabras, las unidades estructurales desaceleran a un ritmo más rápido de lo que predice la ley de Arrhenius. Esta observación se hace razonable suponiendo que las unidades deben superar una barrera de energía por medio de una energía de activación térmica. La energía térmica debe ser lo suficientemente alta como para permitir el movimiento de traslación de las unidades que conduce al flujo viscoso del material.

Véase también

Referencias

  1. ^ ab Arrhenius, SA (1889). "Über die Dissociationswärme und den Einfluß der Temperatur auf den Dissociationsgrad der Elektrolyte". Z. Phys. Química. 4 : 96-116. doi :10.1515/zpch-1889-0408. S2CID  202553486.
  2. ^ ab Arrhenius, SA (1889). "Über die Reaktionsgeschwindigkeit bei der Inversion von Rohrzucker durch Säuren". Z. Phys. Química. 4 : 226–48. doi :10.1515/zpch-1889-0416. S2CID  100032801.
  3. ^ Laidler, KJ (1984). "El desarrollo de la ecuación de Arrhenius". J. Chem. Educ. 61 (6): 494–498. Código Bibliográfico :1984JChEd..61..494L. doi :10.1021/ed061p494.
  4. ^ ab Laidler, KJ (1987) Cinética química , tercera edición, Harper & Row, pág. 42
  5. ^ de Kenneth Connors, Chemical Kinetics, 1990, VCH Publishers Cinética química: el estudio de las velocidades de reacción en solución en Google Books
  6. ^ Definición de la ecuación de Arrhenius según el Libro de Oro de la IUPAC.
  7. ^ Silberberg, Martin S. (2006). Química (cuarta edición). Nueva York: McGraw-Hill. pág. 696. ISBN 0-07-111658-3.
  8. ^ Avery, HE (1974). "4. Dependencia de la velocidad con la temperatura". Basic Reaction Kinetics and Mechanisms. Springer. págs. 47–58 . Consultado el 18 de diciembre de 2023. Sin embargo, la velocidad de reacción varía mucho con la temperatura, ya que para un proceso típico la velocidad se duplica o triplica para un aumento de temperatura de 10 °C.
  9. ^ "6.2.3.3: La ley de Arrhenius – Energías de activación". Chemistry LibreTexts . 2013-10-02.
  10. ^ "15.2: La constante de equilibrio (K)". Chemistry LibreTexts . 2016-03-11 . Consultado el 2023-06-27 .
  11. ^ "Ecuación de Arrhenius" (PDF) . Universidad de Pensilvania . Consultado el 27 de junio de 2023 .
  12. ^ Definición del Libro de Oro de la IUPAC de la ecuación de Arrhenius modificada.
  13. ^ ab Laidler, Keith J.; Meiser, John H. (1982). Química Física (1ª ed.). Benjamín/Cummings. págs. 376–78. ISBN 0-8053-5682-7.
  14. ^ Laidler, Keith J.; Meiser, John H. (1982). Química física (1.ª ed.). Benjamin/Cummings. págs. 378–83. ISBN 0-8053-5682-7.
  15. ^ Levine, RD (2005) Dinámica de reacciones moleculares , Cambridge University Press
  16. ^ Slot, Thierry K.; Riley, Nathan; Shiju, N. Raveendran; Medlin, J. Will; Rothenberg, Gadi (2020). "Un enfoque experimental para controlar los efectos de confinamiento en las interfaces del catalizador". Chemical Science . 11 (40): 11024–11029. doi : 10.1039/D0SC04118A . ISSN  2041-6520. PMC 8162257 . PMID  34123192. 
  17. ^ Bauer, Th.; Lunkenheimer, P.; Loidl, A. (2013). "Cooperatividad y congelamiento del movimiento molecular en la transición vítrea". Physical Review Letters . 111 (22): 225702. arXiv : 1306.4630 . Bibcode :2013PhRvL.111v5702B. doi :10.1103/PhysRevLett.111.225702. PMID  24329455. S2CID  13720989.

Bibliografía

  • Pauling, LC (1988). Química general . Publicaciones de Dover.
  • Laidler, KJ (1987). Cinética química (3.ª ed.). Harper & Row.
  • Laidler, KJ (1993). El mundo de la química física . Oxford University Press.
  • Solubilidad del dióxido de carbono en polietileno: uso de la ecuación de Arrhenius para calcular la solubilidad de las especies en polímeros
Retrieved from "https://en.wikipedia.org/w/index.php?title=Arrhenius_equation&oldid=1251379655"