Reflectancia
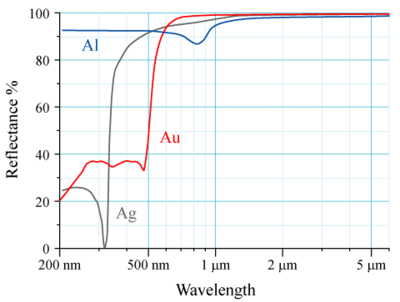
La reflectancia de la superficie de un material es su eficacia para reflejar la energía radiante . Es la fracción de la potencia electromagnética incidente que se refleja en el límite. La reflectancia es un componente de la respuesta de la estructura electrónica del material al campo electromagnético de la luz y, en general, es una función de la frecuencia o longitud de onda de la luz, su polarización y el ángulo de incidencia . La dependencia de la reflectancia con respecto a la longitud de onda se denomina espectro de reflectancia o curva de reflectancia espectral .
Definiciones matemáticas
Reflectancia hemisférica
La reflectancia hemisférica de una superficie, denotada R , se define como [1] donde Φ e r es el flujo radiante reflejado por esa superficie y Φ e i es el flujo radiante recibido por esa superficie.
Reflectancia hemisférica espectral
La reflectancia hemisférica espectral en frecuencia y la reflectancia hemisférica espectral en longitud de onda de una superficie, denotadas R ν y R λ respectivamente, se definen como [1] donde
- Φ e, ν r es el flujo radiante espectral en frecuencia reflejado por esa superficie;
- Φ e, ν i es el flujo radiante espectral en frecuencia recibido por esa superficie;
- Φ e, λ r es el flujo radiante espectral en longitud de onda reflejado por esa superficie;
- Φ e, λ i es el flujo radiante espectral en longitud de onda recibido por esa superficie.
Reflectancia direccional
La reflectancia direccional de una superficie, denotada R Ω , se define como [1] donde
- L e,Ω r es la radiancia reflejada por esa superficie;
- L e,Ω i es la radiancia recibida por esa superficie.
Esto depende tanto de la dirección reflejada como de la dirección entrante. En otras palabras, tiene un valor para cada combinación de direcciones entrantes y salientes. Está relacionado con la función de distribución de reflectancia bidireccional y su límite superior es 1. Otra medida de reflectancia, que depende solo de la dirección saliente, es I / F , donde I es la radiancia reflejada en una dirección dada y F es la radiancia entrante promediada en todas las direcciones, en otras palabras, el flujo total de radiación que golpea la superficie por unidad de área, dividido por π. [2] Esto puede ser mayor que 1 para una superficie brillante iluminada por una fuente como el sol, con la reflectancia medida en la dirección de máxima radiancia (ver también efecto Seeliger ).
Reflectancia direccional espectral
La reflectancia direccional espectral en frecuencia y la reflectancia direccional espectral en longitud de onda de una superficie, denotadas R Ω, ν y R Ω, λ respectivamente, se definen como [1] donde
- L e,Ω, ν r es la radiancia espectral en frecuencia reflejada por esa superficie;
- L e,Ω, ν i es la radiancia espectral recibida por esa superficie;
- L e,Ω, λ r es la radiancia espectral en longitud de onda reflejada por esa superficie;
- L e,Ω, λ i es la radiancia espectral en longitud de onda recibida por esa superficie.
Nuevamente, también se puede definir un valor de I / F (ver arriba) para una longitud de onda dada. [3]
Reflectividad

Para materiales homogéneos y semi-infinitos (ver semiespacio ), la reflectividad es lo mismo que la reflectancia. La reflectividad es el cuadrado de la magnitud del coeficiente de reflexión de Fresnel , [4] que es la relación entre el campo eléctrico reflejado y el campo eléctrico incidente ; [5] como tal, el coeficiente de reflexión se puede expresar como un número complejo según lo determinado por las ecuaciones de Fresnel para una sola capa, mientras que la reflectancia es siempre un número real positivo .
En el caso de medios finitos y estratificados, según la CIE , [ cita requerida ] la reflectividad se distingue de la reflectancia por el hecho de que la reflectancia es un valor que se aplica a objetos reflectantes gruesos . [6] Cuando la reflexión se produce a partir de capas delgadas de material, los efectos de reflexión interna pueden hacer que la reflectancia varíe con el espesor de la superficie. La reflectividad es el valor límite de la reflectancia a medida que la muestra se vuelve más gruesa; es la reflectancia intrínseca de la superficie, por lo tanto, independientemente de otros parámetros como la reflectancia de la superficie trasera. Otra forma de interpretar esto es que la reflectancia es la fracción de potencia electromagnética reflejada desde una muestra específica, mientras que la reflectividad es una propiedad del material en sí, que se mediría en una máquina perfecta si el material llenara la mitad de todo el espacio. [7]
Tipo de superficie
Dado que la reflectancia es una propiedad direccional, la mayoría de las superficies se pueden dividir en aquellas que dan reflexión especular y aquellas que dan reflexión difusa .
En el caso de superficies especulares, como el vidrio o el metal pulido, la reflectancia es casi nula en todos los ángulos, excepto en el ángulo reflejado apropiado; es decir, el mismo ángulo con respecto a la normal de la superficie en el plano de incidencia , pero en el lado opuesto. Cuando la radiación incide de forma normal a la superficie, se refleja de nuevo en la misma dirección.
En el caso de superficies difusas, como la pintura blanca mate, la reflectancia es uniforme; la radiación se refleja en todos los ángulos de manera igual o casi igual. Se dice que estas superficies son lambertianas .
La mayoría de los objetos prácticos exhiben una combinación de propiedades reflectantes difusas y especulares.
Reflectancia del agua

La reflexión se produce cuando la luz pasa de un medio con un índice de refracción a un segundo medio con un índice de refracción diferente.
La reflexión especular de un cuerpo de agua se calcula mediante las ecuaciones de Fresnel . [8] La reflexión de Fresnel es direccional y, por lo tanto, no contribuye significativamente al albedo , que principalmente difunde la reflexión.
Una superficie de agua real puede ser ondulada. La reflectancia, que supone una superficie plana como la que proporcionan las ecuaciones de Fresnel , se puede ajustar para tener en cuenta la ondulación .
Eficiencia de la rejilla
La generalización de la reflectancia a una rejilla de difracción , que dispersa la luz por longitud de onda , se denomina eficiencia de difracción .
Otros coeficientes radiométricos
| Cantidad | Unidades del SI | Notas | |
|---|---|---|---|
| Nombre | Simb. | ||
| Emisividad hemisférica | mi | — | Excitancia radiante de una superficie , dividida por la de un cuerpo negro a la misma temperatura que esa superficie. |
| Emisividad hemisférica espectral | ε ν ε λ | — | Excitancia espectral de una superficie , dividida por la de un cuerpo negro a la misma temperatura que esa superficie. |
| Emisividad direccional | εΩ | — | Radiancia emitida por una superficie , dividida por la emitida por un cuerpo negro a la misma temperatura que esa superficie. |
| Emisividad direccional espectral | εΩ , ν εΩ , λ | — | Radiancia espectral emitida por una superficie , dividida por la de un cuerpo negro a la misma temperatura que esa superficie. |
| Absorbancia hemisférica | A | — | Flujo radiante absorbido por una superficie , dividido por el que recibe dicha superficie. No debe confundirse con " absorbancia ". |
| Absorción hemisférica espectral | Una ν Una λ | — | Flujo espectral absorbido por una superficie , dividido por el que recibe dicha superficie. No debe confundirse con la " absorbancia espectral ". |
| Absorbancia direccional | Un Ω | — | Radiancia absorbida por una superficie , dividida por la radiancia incidente sobre esa superficie. No debe confundirse con " absorbancia ". |
| Absorbancia direccional espectral | Un Ω, ν Un Ω, λ | — | Radiancia espectral absorbida por una superficie , dividida por la radiancia espectral incidente sobre esa superficie. No debe confundirse con " absorbancia espectral ". |
| Reflectancia hemisférica | R | — | Flujo radiante reflejado por una superficie , dividido por el recibido por esa superficie. |
| Reflectancia hemisférica espectral | R ν R λ | — | Flujo espectral reflejado por una superficie , dividido por el recibido por esa superficie. |
| Reflectancia direccional | RΩ | — | Radiancia reflejada por una superficie , dividida por la recibida por esa superficie. |
| Reflectancia direccional espectral | RΩ , ν RΩ , λ | — | Radiancia espectral reflejada por una superficie , dividida por la recibida por esa superficie. |
| Transmitancia hemisférica | yo | — | Flujo radiante transmitido por una superficie , dividido por el recibido por esa superficie. |
| Transmitancia hemisférica espectral | Tν Tλ | — | Flujo espectral transmitido por una superficie , dividido por el recibido por esa superficie. |
| Transmitancia direccional | TΩ | — | Radiancia transmitida por una superficie , dividida por la recibida por esa superficie. |
| Transmitancia direccional espectral | TΩ ,ν TΩ , λ | — | Radiancia espectral transmitida por una superficie , dividida por la recibida por esa superficie. |
| Coeficiente de atenuación hemisférico | micras | m -1 | Flujo radiante absorbido y dispersado por un volumen por unidad de longitud, dividido por el recibido por ese volumen. |
| Coeficiente de atenuación hemisférica espectral | μνμλ | m -1 | Flujo radiante espectral absorbido y dispersado por un volumen por unidad de longitud, dividido por el recibido por ese volumen. |
| Coeficiente de atenuación direccional | μΩ | m -1 | Radiancia absorbida y dispersada por un volumen por unidad de longitud, dividida por la recibida por ese volumen. |
| Coeficiente de atenuación direccional espectral | μΩ , ν μΩ , λ | m -1 | Radiancia espectral absorbida y dispersada por un volumen por unidad de longitud, dividida por la recibida por ese volumen. |
Véase también
- Función de distribución de reflectancia bidireccional
- Colorimetría
- Emisividad
- Ley del coseno de Lambert
- Transmitancia
- Camino del sol
- Valor de reflectancia de la luz
- Albedo
- Efecto de la radiación de reposo
- Relación Lyddane-Sachs-Teller
Referencias
- ^ abcd «Aislamiento térmico. Transferencia de calor por radiación. Magnitudes físicas y definiciones». ISO 9288:1989 . Catálogo ISO . 1989. Consultado el 15 de marzo de 2015 .
- ^ Cuzzi, Jeffrey; Chambers, Lindsey; Hendrix, Amanda (21 de octubre de 2016). "Superficies rugosas: ¿la materia oscura es solo sombra?". Icarus . 289 : 281–294. doi :10.1016/j.icarus.2016.10.018. PMC 6839776 . PMID 31708591.
- ^ Véase, por ejemplo, PGJ Irwin; et al. (12 de enero de 2022). "Mundos azules brumosos: un modelo holístico de aerosoles para Urano y Neptuno, incluidas las manchas oscuras". Revista de investigación geofísica: planetas . 127 (6): e2022JE007189. arXiv : 2201.04516 . Bibcode : 2022JGRE..12707189I . doi : 10.1029/2022JE007189 . hdl : 1983/65ee78f0-1d28-4017-bbd9-1b49b24700d7 . PMC 9286428 . PMID 35865671. S2CID 245877540 .
- ^ E. Hecht (2001). Óptica (4ª ed.). Educación Pearson. ISBN 0-8053-8566-5 .
- ^ IUPAC , Compendio de terminología química , 2.ª edición (el "Libro de oro") (1997). Versión corregida en línea: (2006–) "Reflectancia". doi :10.1351/goldbook.R05235
- ^ "Vocabulario internacional de iluminación CIE". Archivado desde el original el 16 de junio de 2016. Consultado el 4 de diciembre de 2010 .
- ^ Palmer y Grant, El arte de la radiometría
- ^ Ottaviani, M. y Stamnes, K. y Koskulics, J. y Eide, H. y Long, SR y Su, W. y Wiscombe, W., 2008: 'Reflexión de la luz de las ondas de agua: configuración adecuada para una investigación polarimétrica en condiciones de laboratorio controladas' . Revista de tecnología atmosférica y oceánica, 25 (5) , 715--728.
Enlaces externos
- Reflectividad de los metales Archivado el 4 de marzo de 2016 en Wayback Machine .
- Datos de reflectancia.






