Longitud de onda

En física y matemáticas , la longitud de onda o período espacial de una onda o función periódica es la distancia sobre la cual se repite la forma de la onda. ^{[1] [2]} En otras palabras, es la distancia entre puntos consecutivos correspondientes de la misma fase en la onda, como dos crestas, valles o cruces por cero adyacentes . La longitud de onda es una característica tanto de las ondas viajeras como de las ondas estacionarias , así como de otros patrones de ondas espaciales. ^{[3] [4]} La inversa de la longitud de onda se llama frecuencia espacial . La longitud de onda se designa comúnmente con la letra griega lambda ( λ ). El término "longitud de onda" también se aplica a veces a las ondas moduladas y a las envolventes sinusoidales de las ondas moduladas o las ondas formadas por la interferencia de varias sinusoides. ^[5]

Suponiendo una onda sinusoidal que se mueve a una velocidad de onda fija, la longitud de onda es inversamente proporcional a la frecuencia de la onda: las ondas con frecuencias más altas tienen longitudes de onda más cortas y las frecuencias más bajas tienen longitudes de onda más largas. ^[6]

La longitud de onda depende del medio (por ejemplo, vacío, aire o agua) por el que viaja una onda. Ejemplos de ondas son las ondas sonoras , la luz , las ondas de agua y las señales eléctricas periódicas en un conductor . Una onda sonora es una variación en la presión del aire , mientras que en la luz y otras radiaciones electromagnéticas la fuerza del campo eléctrico y magnético varía. Las ondas de agua son variaciones en la altura de una masa de agua. En una vibración de red cristalina , las posiciones atómicas varían.

El rango de longitudes de onda o frecuencias de los fenómenos ondulatorios se denomina espectro . El nombre se originó con el espectro de luz visible , pero ahora se puede aplicar a todo el espectro electromagnético , así como al espectro del sonido o al espectro de vibración .

En medios lineales , cualquier patrón de onda puede describirse en términos de la propagación independiente de componentes sinusoidales. La longitud de onda λ de una forma de onda sinusoidal que viaja a velocidad constante está dada por ^[7]${\estilo de visualización v}$

${\displaystyle \lambda ={\frac {v}{f}}\,\,,}$

donde se denomina velocidad de fase (magnitud de la velocidad de fase ) de la onda y es la frecuencia de la onda . En un medio dispersivo , la velocidad de fase depende de la frecuencia de la onda, lo que hace que la relación entre longitud de onda y frecuencia no sea lineal.${\estilo de visualización v}$${\estilo de visualización f}$

En el caso de la radiación electromagnética —como la luz— en el espacio libre , la velocidad de fase es la velocidad de la luz , aproximadamente3 × 10 ⁸  m/s . Por lo tanto, la longitud de onda de una onda electromagnética (radio) de 100 MHz es aproximadamente:3 × 10 ⁸  m/s dividido por10 ⁸  Hz = 3 m. La longitud de onda de la luz visible varía desde el rojo intenso , aproximadamente 700  nm , hasta el violeta , aproximadamente 400 nm (para otros ejemplos, consulte espectro electromagnético ).

En el caso de las ondas sonoras en el aire, la velocidad del sonido es de 343 m/s (a temperatura ambiente y presión atmosférica ). Las longitudes de onda de las frecuencias sonoras audibles para el oído humano (20  Hz – 20 kHz) se encuentran, por tanto, entre aproximadamente 17  m y 17  mm , respectivamente. Los murciélagos utilizan frecuencias algo más altas para poder distinguir objetos de menos de 17 mm. Las longitudes de onda del sonido audible son mucho mayores que las de la luz visible.

Una onda estacionaria es un movimiento ondulatorio que permanece en un lugar. Una onda estacionaria sinusoidal incluye puntos estacionarios sin movimiento, llamados nodos , y la longitud de onda es el doble de la distancia entre nodos.

La figura superior muestra tres ondas estacionarias en una caja. Se considera que las paredes de la caja requieren que la onda tenga nodos en las paredes de la caja (un ejemplo de condiciones de contorno ), lo que determina las longitudes de onda permitidas. Por ejemplo, para una onda electromagnética, si la caja tiene paredes conductoras ideales, la condición para los nodos en las paredes se cumple porque las paredes conductoras no pueden soportar un campo eléctrico tangencial, lo que obliga a la onda a tener una amplitud cero en la pared.

La onda estacionaria puede considerarse como la suma de dos ondas sinusoidales que viajan con velocidades opuestas. ^[8] En consecuencia, la longitud de onda, el período y la velocidad de onda están relacionados, al igual que en el caso de una onda viajera. Por ejemplo, la velocidad de la luz puede determinarse a partir de la observación de ondas estacionarias en una caja de metal que contiene un vacío ideal.

Las ondas sinusoidales que viajan a menudo se representan matemáticamente en términos de su velocidad v (en la dirección x), frecuencia f y longitud de onda λ como:

${\displaystyle y(x,\t)=A\cos \left(2\pi \left({\frac {x}{\lambda }}-ft\right)\right)=A\cos \left({\frac {2\pi }{\lambda }}(x-vt)\right)}$

donde y es el valor de la onda en cualquier posición x y tiempo t , y A es la amplitud de la onda. También se expresan comúnmente en términos de número de onda k (2π multiplicado por el recíproco de la longitud de onda) y frecuencia angular ω (2π multiplicado por la frecuencia) como:

${\displaystyle y(x,\t)=A\cos \left(kx-\omega t\right)=A\cos \left(k(x-vt)\right)}$

en el que la longitud de onda y el número de onda están relacionados con la velocidad y la frecuencia como:

${\displaystyle k={\frac {2\pi }{\lambda }}={\frac {2\pi f}{v}}={\frac {\omega }{v}},}$

o

${\displaystyle \lambda ={\frac {2\pi }{k}}={\frac {2\pi v}{\omega }}={\frac {v}{f}}.}$

En la segunda forma dada arriba, la fase ( kx − ωt ) se generaliza a menudo a ( k ⋅ r − ωt ) , reemplazando el número de onda k con un vector de onda que especifica la dirección y el número de onda de una onda plana en el espacio tridimensional , parametrizado por el vector de posición r . En ese caso, el número de onda k , la magnitud de k , todavía está en la misma relación con la longitud de onda como se muestra arriba, con v siendo interpretado como velocidad escalar en la dirección del vector de onda. La primera forma, usando la longitud de onda recíproca en la fase, no se generaliza tan fácilmente a una onda en una dirección arbitraria.

También son comunes las generalizaciones a senos de otras fases y a exponenciales complejas; véase onda plana . La convención típica de utilizar la fase del coseno en lugar de la fase del seno al describir una onda se basa en el hecho de que el coseno es la parte real de la exponencial compleja en la onda.

${\displaystyle Ae^{i\left(kx-\omega t\right)}.}$

La velocidad de una onda depende del medio en el que se propaga. En particular, la velocidad de la luz en un medio es menor que en el vacío , lo que significa que la misma frecuencia corresponderá a una longitud de onda más corta en el medio que en el vacío, como se muestra en la figura de la derecha.

Este cambio de velocidad al entrar en un medio provoca la refracción , o un cambio en la dirección de las ondas que encuentran la interfaz entre los medios en un ángulo. ^[9] Para las ondas electromagnéticas , este cambio en el ángulo de propagación está regido por la ley de Snell .

La velocidad de onda en un medio no sólo puede ser diferente a la de otro, sino que también varía con la longitud de onda. Como resultado, el cambio de dirección al entrar en un medio diferente cambia con la longitud de onda de la onda.

Para las ondas electromagnéticas, la velocidad en un medio está determinada por su índice de refracción según

${\displaystyle v={\frac {c}{n(\lambda _ {0})}},}$

donde c es la velocidad de la luz en el vacío y n ( λ ₀ ) es el índice de refracción del medio en la longitud de onda λ ₀ , donde este último se mide en el vacío en lugar de en el medio. La longitud de onda correspondiente en el medio es

${\displaystyle \lambda ={\frac {\lambda _{0}}{n(\lambda _{0})}}.}$

Cuando se indican longitudes de onda de radiación electromagnética, normalmente se hace referencia a la longitud de onda en el vacío, a menos que se identifique específicamente que la longitud de onda es la longitud de onda en algún otro medio. En acústica, donde un medio es esencial para que existan las ondas, el valor de la longitud de onda se proporciona para un medio específico.

La variación de la velocidad de la luz con la longitud de onda se conoce como dispersión y también es responsable del fenómeno conocido en el que la luz se separa en colores componentes por un prisma . La separación se produce cuando el índice de refracción dentro del prisma varía con la longitud de onda, por lo que las diferentes longitudes de onda se propagan a diferentes velocidades dentro del prisma, lo que hace que se refracten en diferentes ángulos. La relación matemática que describe cómo varía la velocidad de la luz dentro de un medio con la longitud de onda se conoce como relación de dispersión .

La longitud de onda puede ser un concepto útil incluso si la onda no es periódica en el espacio. Por ejemplo, en una ola oceánica que se acerca a la costa, como se muestra en la figura, la onda entrante ondula con una longitud de onda local variable que depende en parte de la profundidad del fondo marino en comparación con la altura de la ola. El análisis de la onda puede basarse en la comparación de la longitud de onda local con la profundidad del agua local. ^[10]

Las ondas que son sinusoidales en el tiempo pero que se propagan a través de un medio cuyas propiedades varían con la posición (un medio no homogéneo ) pueden propagarse a una velocidad que varía con la posición y, como resultado, pueden no ser sinusoidales en el espacio. La figura de la derecha muestra un ejemplo. A medida que la onda se ralentiza, la longitud de onda se acorta y la amplitud aumenta; después de un lugar de respuesta máxima, la longitud de onda corta se asocia con una pérdida alta y la onda se extingue.

El análisis de ecuaciones diferenciales de tales sistemas se realiza a menudo de forma aproximada, utilizando el método WKB (también conocido como el método de Liouville-Green ). El método integra la fase a través del espacio utilizando un número de onda local , que puede interpretarse como una indicación de una "longitud de onda local" de la solución en función del tiempo y el espacio. ^{[11] [12]} Este método trata el sistema localmente como si fuera uniforme con las propiedades locales; en particular, la velocidad de onda local asociada con una frecuencia es lo único necesario para estimar el número de onda o longitud de onda local correspondiente. Además, el método calcula una amplitud que cambia lentamente para satisfacer otras restricciones de las ecuaciones o del sistema físico, como la conservación de la energía en la onda.

Las ondas en los sólidos cristalinos no son continuas, porque están compuestas por vibraciones de partículas discretas dispuestas en una red regular. Esto produce aliasing porque se puede considerar que la misma vibración tiene una variedad de longitudes de onda diferentes, como se muestra en la figura. ^[13] Las descripciones que utilizan más de una de estas longitudes de onda son redundantes; es convencional elegir la longitud de onda más larga que se ajuste al fenómeno. El rango de longitudes de onda suficiente para proporcionar una descripción de todas las ondas posibles en un medio cristalino corresponde a los vectores de onda confinados a la zona de Brillouin . ^[14]

Esta indeterminación de la longitud de onda en los sólidos es importante para el análisis de fenómenos ondulatorios como las bandas de energía y las vibraciones reticulares . Es matemáticamente equivalente al aliasing de una señal que se muestrea a intervalos discretos.

El concepto de longitud de onda se aplica con mayor frecuencia a ondas sinusoidales o casi sinusoidales, porque en un sistema lineal la sinusoide es la única forma que se propaga sin cambio de forma, solo un cambio de fase y potencialmente un cambio de amplitud. ^[15] La longitud de onda (o alternativamente el número de onda o el vector de onda ) es una caracterización de la onda en el espacio, que está funcionalmente relacionada con su frecuencia, según lo restringido por la física del sistema. Las sinusoides son las soluciones de onda viajera más simples , y se pueden construir soluciones más complejas por superposición .

En el caso especial de medios libres de dispersión y uniformes, las ondas distintas de las sinusoides se propagan con una forma invariable y una velocidad constante. En determinadas circunstancias, también pueden producirse ondas de forma invariable en medios no lineales; por ejemplo, la figura muestra ondas oceánicas en aguas poco profundas que tienen crestas más pronunciadas y valles más planos que los de una sinusoide, típicas de una onda cnoidal ^[16] , una onda viajera llamada así porque se describe mediante la función elíptica de Jacobi de orden m , normalmente denotada como cn ( x ; m ) . ^[17] Las ondas oceánicas de gran amplitud con determinadas formas pueden propagarse sin cambios, debido a las propiedades del medio de ondas superficiales no lineales. ^[18]

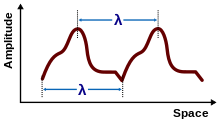
Si una onda viajera tiene una forma fija que se repite en el espacio o en el tiempo, es una onda periódica . ^[19] A veces se considera que estas ondas tienen una longitud de onda aunque no sean sinusoidales. ^[20] Como se muestra en la figura, la longitud de onda se mide entre puntos correspondientes consecutivos en la forma de onda.

Los paquetes de ondas localizados , "ráfagas" de acción de las ondas en las que cada paquete de ondas viaja como una unidad, encuentran aplicación en muchos campos de la física. Un paquete de ondas tiene una envolvente que describe la amplitud general de la onda; dentro de la envolvente, la distancia entre picos o valles adyacentes a veces se denomina longitud de onda local . ^{[21] [22]} En la figura se muestra un ejemplo. En general, la envolvente del paquete de ondas se mueve a una velocidad diferente de las ondas constituyentes. ^[23]

Utilizando el análisis de Fourier , los paquetes de ondas se pueden analizar en sumas infinitas (o integrales) de ondas sinusoidales de diferentes números de onda o longitudes de onda. ^[24]

Louis de Broglie postuló que todas las partículas con un valor específico de momento p tienen una longitud de onda λ = h / p , donde h es la constante de Planck . Esta hipótesis fue la base de la mecánica cuántica . Hoy en día, esta longitud de onda se llama longitud de onda de De Broglie . Por ejemplo, los electrones en una pantalla CRT tienen una longitud de onda de De Broglie de aproximadamente10 ⁻¹³  m . Para evitar que la función de onda de una partícula de este tipo se extienda por todo el espacio, de Broglie propuso utilizar paquetes de ondas para representar partículas que están localizadas en el espacio. ^[25] La extensión espacial del paquete de ondas y la extensión de los números de onda de las sinusoides que forman el paquete corresponden a las incertidumbres en la posición y el momento de la partícula, cuyo producto está limitado por el principio de incertidumbre de Heisenberg . ^[24]

Cuando las formas de onda sinusoidales se suman, pueden reforzarse entre sí (interferencia constructiva) o cancelarse entre sí (interferencia destructiva) dependiendo de su fase relativa. Este fenómeno se utiliza en el interferómetro . Un ejemplo sencillo es un experimento debido a Young donde la luz pasa a través de dos rendijas . ^[26] Como se muestra en la figura, la luz pasa a través de dos rendijas y brilla sobre una pantalla. La trayectoria de la luz a una posición en la pantalla es diferente para las dos rendijas, y depende del ángulo θ que la trayectoria forma con la pantalla. Si suponemos que la pantalla está lo suficientemente lejos de las rendijas (es decir, s es grande en comparación con la separación de rendijas d ), entonces las trayectorias son casi paralelas, y la diferencia de trayectorias es simplemente d sen θ . En consecuencia, la condición para la interferencia constructiva es: ^[27]

${\displaystyle d\sin \theta =m\lambda \ ,}$

donde m es un número entero, y para la interferencia destructiva es:

${\displaystyle d\sin \theta =(m+1/2)\lambda \ .}$

Así, si se conoce la longitud de onda de la luz, se puede determinar la separación de las rendijas a partir del patrón de interferencia o franjas , y viceversa .

Para ranuras múltiples, el patrón es ^[28]

${\displaystyle I_{q}=I_{1}\sin ^{2}\left({\frac {q\pi g\sin \alpha }{\lambda }}\right)/\sin ^{2}\left({\frac {\pi g\sin \alpha }{\lambda }}\right)\ ,}$

donde q es el número de rendijas y g es la constante de la rejilla. El primer factor, I ₁ , es el resultado de una sola rendija, que modula el segundo factor, que varía más rápidamente y depende del número de rendijas y su espaciamiento. En la figura, I ₁ se ha establecido en la unidad, una aproximación muy aproximada.

El efecto de la interferencia es redistribuir la luz, de modo que la energía contenida en ella no se altera, sólo aparece donde aparece. ^[29]

La noción de diferencia de trayectorias e interferencia constructiva o destructiva utilizada anteriormente para el experimento de la doble rendija se aplica también a la visualización de una única rendija de luz interceptada en una pantalla. El resultado principal de esta interferencia es la dispersión de la luz procedente de la rendija estrecha en una imagen más amplia en la pantalla. Esta distribución de la energía de las ondas se denomina difracción .

Se distinguen dos tipos de difracción según la separación entre la fuente y la pantalla: difracción de Fraunhofer o difracción de campo lejano a grandes separaciones y difracción de Fresnel o difracción de campo cercano a pequeñas separaciones.

En el análisis de la rendija única se tiene en cuenta el ancho distinto de cero de la rendija y cada punto de la abertura se toma como la fuente de una contribución al haz de luz ( wavelets de Huygens ). En la pantalla, la luz que llega desde cada posición dentro de la rendija tiene una longitud de recorrido diferente, aunque posiblemente una diferencia muy pequeña. En consecuencia, se producen interferencias.

En el patrón de difracción de Fraunhofer suficientemente alejado de una sola rendija, dentro de una aproximación de ángulo pequeño , la dispersión de intensidad S está relacionada con la posición x a través de una función sinc al cuadrado : ^[30]

${\displaystyle S(u)=\mathrm {sinc} ^{2}(u)=\left({\frac {\sin \pi u}{\pi u}}\right)^{2}\ ;}$  con  ${\displaystyle u={\frac {xL}{\lambda R}}\ ,}$

donde L es el ancho de la rendija, R es la distancia del patrón (en la pantalla) desde la rendija y λ es la longitud de onda de la luz utilizada. La función S tiene ceros donde u es un entero distinto de cero, donde son valores x con una separación proporcional a la longitud de onda.

La difracción es la limitación fundamental del poder de resolución de los instrumentos ópticos, como los telescopios (incluidos los radiotelescopios ) y los microscopios . ^[31] Para una apertura circular, el punto de imagen limitado por difracción se conoce como disco de Airy ; la distancia x en la fórmula de difracción de rendija única se reemplaza por la distancia radial r y el seno se reemplaza por 2 J ₁ , donde J ₁ es una función de Bessel de primer orden . ^[32]

El tamaño espacial resoluble de los objetos observados a través de un microscopio está limitado según el criterio de Rayleigh , el radio del primer nulo del disco de Airy, a un tamaño proporcional a la longitud de onda de la luz utilizada, y dependiendo de la apertura numérica : ^[33]

${\displaystyle r_{Airy}=1.22{\frac {\lambda }{2\,\mathrm {NA} }}\ ,}$

donde la apertura numérica se define como θ siendo el semiángulo del cono de rayos aceptado por el objetivo del microscopio .${\displaystyle \mathrm {NA} =n\sin \theta \;}$

El tamaño angular de la porción brillante central (radio del primer nulo del disco de Airy ) de la imagen difractada por una apertura circular, una medida más comúnmente utilizada para telescopios y cámaras, es: ^[34]

${\displaystyle \delta =1,22{\frac {\lambda }{D}}\ ,}$

donde λ es la longitud de onda de las ondas que se enfocan para la obtención de imágenes, D es el diámetro de la pupila de entrada del sistema de obtención de imágenes, en las mismas unidades, y la resolución angular δ está en radianes.

Al igual que con otros patrones de difracción, el patrón se escala en proporción a la longitud de onda, por lo que las longitudes de onda más cortas pueden generar una mayor resolución.

El término sublongitud de onda se utiliza para describir un objeto que tiene una o más dimensiones menores que la longitud de onda con la que interactúa el objeto. Por ejemplo, el término fibra óptica de diámetro sublongitud de onda significa una fibra óptica cuyo diámetro es menor que la longitud de onda de la luz que se propaga a través de ella.

Una partícula de sublongitud de onda es una partícula más pequeña que la longitud de onda de la luz con la que interactúa (ver dispersión de Rayleigh ). Las aberturas de sublongitud de onda son agujeros más pequeños que la longitud de onda de la luz que se propaga a través de ellos. Estas estructuras tienen aplicaciones en la transmisión óptica extraordinaria y en las guías de onda de modo cero , entre otras áreas de la fotónica .

La sublongitud de onda también puede referirse a un fenómeno que involucra objetos de sublongitud de onda; por ejemplo, imágenes de sublongitud de onda .

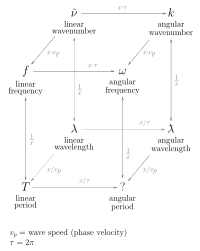
Una cantidad relacionada con la longitud de onda es la longitud de onda angular (también conocida como longitud de onda reducida ), usualmente simbolizada por ƛ ("lambda-barra" o lambda barrada ). Es igual a la longitud de onda ordinaria reducida por un factor de 2π ( ƛ = λ /2π ), con unidades del SI de metro por radián. Es la inversa del número de onda angular ( k = 2π/ λ ). Usualmente se encuentra en mecánica cuántica, donde se usa en combinación con la constante de Planck reducida (símbolo  ħ , h-barra) y la frecuencia angular (símbolo  ω = 2π f ).

• Espectro de emisión
• Envolvente (ondas)
• Líneas de Fraunhofer : líneas oscuras en el espectro solar, utilizadas tradicionalmente como referencias de longitud de onda óptica estándar
• Índice de artículos sobre olas
• Medición de longitud
• Línea espectral
• Espectroscopia
• Espectro

Wikimedia Commons tiene medios relacionados con Longitud de onda .

• Conversión: Longitud de onda a frecuencia y viceversa – Ondas sonoras y ondas de radio
• Recurso didáctico para niños de 14 a 16 años sobre el sonido, incluida la longitud de onda Archivado el 13 de marzo de 2012 en Wayback Machine.
• El espectro electromagnético visible mostrado en colores web con longitudes de onda correspondientes