Plano inclinado
Superficie de apoyo plana inclinada

Rampa para sillas de ruedas , Hotel Montescot, Chartres, Francia
Demostración del plano inclinado utilizado en la educación, Museo Galileo , Florencia.

Un plano inclinado , también conocido como rampa , es una superficie de apoyo plana inclinada en un ángulo con respecto a la dirección vertical , con un extremo más alto que el otro, que se utiliza como ayuda para subir o bajar una carga. [1] [2] [3] El plano inclinado es una de las seis máquinas simples clásicas definidas por los científicos del Renacimiento. Los planos inclinados se utilizan para mover cargas pesadas sobre obstáculos verticales. Los ejemplos varían desde una rampa utilizada para cargar mercancías en un camión, hasta una persona que sube una rampa para peatones, hasta un automóvil o un tren que sube una pendiente. [3]

Para mover un objeto por un plano inclinado se necesita menos fuerza que para levantarlo en línea recta, pero se aumenta la distancia recorrida. [4] La ventaja mecánica de un plano inclinado, el factor por el cual se reduce la fuerza, es igual a la relación entre la longitud de la superficie inclinada y la altura que abarca. Debido a la conservación de la energía , se requiere la misma cantidad de energía mecánica ( trabajo ) para levantar un objeto dado una distancia vertical dada , sin tener en cuenta las pérdidas por fricción , pero el plano inclinado permite realizar el mismo trabajo con una fuerza menor ejercida sobre una distancia mayor. [5] [6]

El ángulo de fricción , [7] también llamado a veces ángulo de reposo , [8] es el ángulo máximo en el que una carga puede permanecer inmóvil sobre un plano inclinado debido a la fricción sin deslizarse hacia abajo. Este ángulo es igual a la arcotangente del coeficiente de fricción estática μ s entre las superficies. [8]

A menudo se considera que otras dos máquinas simples se derivan del plano inclinado. [9] La cuña puede considerarse un plano inclinado móvil o dos planos inclinados conectados en la base. [5] El tornillo consiste en un plano inclinado estrecho que envuelve un cilindro . [5]

El término también puede referirse a una implementación específica; una rampa recta cortada en una ladera empinada para transportar mercancías hacia arriba y hacia abajo por la colina. Esto puede incluir automóviles sobre rieles o tirados por un sistema de cable; un funicular o un teleférico , como el Johnstown Inclined Plane .

Usos

Los planos inclinados se utilizan ampliamente en forma de rampas de carga para cargar y descargar mercancías en camiones, barcos y aviones. [3] Las rampas para sillas de ruedas se utilizan para permitir que las personas en sillas de ruedas superen obstáculos verticales sin exceder su fuerza. Las escaleras mecánicas y las cintas transportadoras inclinadas también son formas de plano inclinado. [6] En un funicular o teleférico, un vagón de ferrocarril se sube por un plano inclinado pronunciado mediante cables. Los planos inclinados también permiten que objetos pesados ​​y frágiles, incluidos los humanos, bajen de forma segura una distancia vertical utilizando la fuerza normal del avión para reducir la fuerza gravitacional . Los toboganes de evacuación de aeronaves permiten que las personas lleguen al suelo de forma rápida y segura desde la altura de un avión de pasajeros .

Otros planos inclinados se construyen en estructuras permanentes. Las carreteras para vehículos y ferrocarriles tienen planos inclinados en forma de pendientes graduales, rampas y calzadas para permitir que los vehículos superen obstáculos verticales como colinas sin perder tracción en la superficie de la carretera. [3] De manera similar, los caminos peatonales y las aceras tienen rampas suaves para limitar su pendiente, para garantizar que los peatones puedan mantener la tracción. [1] [4] Los planos inclinados también se utilizan como entretenimiento para que la gente se deslice de manera controlada, en toboganes de juegos , toboganes de agua , pistas de esquí y parques de patinetas .


Historia

La prueba de Stevin
En 1586, el ingeniero flamenco Simon Stevin (Stevinus) dedujo la ventaja mecánica del plano inclinado mediante un argumento que utilizaba una sarta de cuentas. [10] Imaginó dos planos inclinados de igual altura pero con diferentes pendientes, colocados uno detrás del otro como en un prisma ( A, B, C arriba). Un bucle de cuerda con cuentas a intervalos iguales se coloca sobre los planos inclinados, con una parte de la cuerda colgando hacia abajo. Las cuentas que descansan sobre los planos actúan como cargas sobre los planos, sostenidas por la fuerza de tensión de la cuerda en el punto T. El argumento de Stevin es el siguiente: [10] [11] [12]
  • La cuerda debe estar estacionaria, en equilibrio estático . Si la cuerda fuera más pesada en un lado que en el otro, y comenzara a deslizarse hacia la derecha o hacia la izquierda por su propio peso, cuando cada cuenta se hubiera movido a la posición de la cuenta anterior, la cuerda sería indistinguible de su posición inicial y, por lo tanto, continuaría desequilibrada y deslizándose. Este argumento podría repetirse indefinidamente, lo que daría como resultado un movimiento perpetuo circular , lo cual es absurdo. Por lo tanto, es estacionaria, con las fuerzas en los dos lados en el punto T ( arriba ) iguales.
  • La parte de la cadena que cuelga debajo de los planos inclinados es simétrica, con un número igual de cuentas en cada lado. Ejerce una fuerza igual en cada lado de la cuerda. Por lo tanto, esta parte de la cuerda se puede cortar en los bordes de los planos (puntos S y V) , dejando solo las cuentas apoyadas en los planos inclinados, y esta parte restante seguirá estando en equilibrio estático.
  • Como las cuentas están a intervalos iguales en la cuerda, el número total de cuentas soportadas por cada plano, la carga total, es proporcional a la longitud del plano. Como la fuerza de soporte de entrada, la tensión en la cuerda, es la misma para ambos, la ventaja mecánica de cada plano es proporcional a su longitud oblicua.

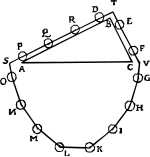
Como señala Dijksterhuis, [13] el argumento de Stevin no es completamente sólido. Las fuerzas ejercidas por la parte colgante de la cadena no necesitan ser simétricas porque la parte colgante no necesita conservar su forma cuando se suelta. Incluso si la cadena se suelta con un momento angular cero, el movimiento, incluidas las oscilaciones, es posible a menos que la cadena esté inicialmente en su configuración de equilibrio, una suposición que haría que el argumento fuera circular.

Los planos inclinados han sido utilizados por las personas desde tiempos prehistóricos para mover objetos pesados. [14] [15] Los caminos inclinados y las calzadas construidas por civilizaciones antiguas como los romanos son ejemplos de planos inclinados tempranos que han sobrevivido y muestran que entendieron el valor de este dispositivo para mover cosas cuesta arriba. Se cree que las piedras pesadas utilizadas en antiguas estructuras de piedra como Stonehenge [16] se movieron y colocaron en su lugar utilizando planos inclinados hechos de tierra, [17] aunque es difícil encontrar evidencia de tales rampas de construcción temporales. Las pirámides egipcias se construyeron utilizando planos inclinados, [18] [19] [20] Las rampas de asedio permitieron a los ejércitos antiguos superar los muros de las fortalezas. Los antiguos griegos construyeron una rampa pavimentada de 6 km (3,7 millas) de largo, el Diolkos , para arrastrar barcos por tierra a través del istmo de Corinto . [4]

Sin embargo, el plano inclinado fue la última de las seis máquinas simples clásicas en ser reconocida como una máquina. Esto se debe probablemente a que es un dispositivo pasivo e inmóvil (la carga es la parte móvil), [21] y también porque se encuentra en la naturaleza en forma de pendientes y colinas. Aunque entendían su uso para levantar objetos pesados, los filósofos griegos antiguos que definieron las otras cinco máquinas simples no incluyeron el plano inclinado como una máquina. [22] Esta visión persistió entre algunos científicos posteriores; tan tarde como en 1826 Karl von Langsdorf escribió que un plano inclinado " ... no es más una máquina que la pendiente de una montaña ". [21] El problema de calcular la fuerza necesaria para empujar un peso hacia arriba en un plano inclinado (su ventaja mecánica) fue intentado por los filósofos griegos Herón de Alejandría (c. 10 - 60 d. C.) y Pappus de Alejandría (c. 290 - 350 d. C.), pero sus soluciones eran incorrectas. [23] [24] [25]

No fue hasta el Renacimiento que el plano inclinado fue resuelto matemáticamente y clasificado con las otras máquinas simples. El primer análisis correcto del plano inclinado apareció en la obra del autor del siglo XIII Jordanus de Nemore , [26] [27] sin embargo su solución aparentemente no fue comunicada a otros filósofos de la época. [24] Girolamo Cardano (1570) propuso la solución incorrecta de que la fuerza de entrada es proporcional al ángulo del plano. [10] Luego, a fines del siglo XVI, se publicaron tres soluciones correctas en diez años, por Michael Varro (1584), Simon Stevin (1586) y Galileo Galilei (1592). [24] Aunque no fue la primera, la derivación del ingeniero flamenco Simon Stevin [25] es la más conocida, debido a su originalidad y al uso de un collar de cuentas (ver recuadro). [12] [26] En 1600, el científico italiano Galileo Galilei incluyó el plano inclinado en su análisis de máquinas simples en Le Meccaniche ("Sobre la mecánica"), mostrando su similitud subyacente con las otras máquinas como amplificador de fuerza. [28]

Las primeras reglas elementales de fricción por deslizamiento en un plano inclinado fueron descubiertas por Leonardo da Vinci (1452-1519), pero permanecieron inéditas en sus cuadernos. [29] Fueron redescubiertas por Guillaume Amontons (1699) y desarrolladas posteriormente por Charles-Augustin de Coulomb (1785). [29] Leonhard Euler (1750) demostró que la tangente del ángulo de reposo en un plano inclinado es igual al coeficiente de fricción . [30]

Terminología

Pendiente

La ventaja mecánica de un plano inclinado depende de su pendiente , es decir, de su gradiente o inclinación. Cuanto menor sea la pendiente, mayor será la ventaja mecánica y menor será la fuerza necesaria para elevar un peso determinado. La pendiente de un plano s es igual a la diferencia de altura entre sus dos extremos, o " elevación ", dividida por su longitud horizontal, o " recorrido ". [31] También se puede expresar mediante el ángulo que forma el plano con la horizontal, . θ {\estilo de visualización \theta}

La geometría del plano inclinado se basa en un triángulo rectángulo . [31] La longitud horizontal a veces se denomina Run y ​​el cambio vertical en altura Rise .
θ = broncearse − 1 ⁡ ( Elevar Correr ) {\displaystyle \theta =\tan ^{-1}{\bigg (}{\frac {\text{Ascenso}}{\text{Carrera}}}{\bigg )}\,}

Ventaja mecánica

La ventaja mecánica de una máquina simple se define como la relación entre la fuerza de salida ejercida sobre la carga y la fuerza de entrada aplicada. En el plano inclinado, la fuerza de salida de la carga es simplemente la fuerza gravitacional del objeto de carga sobre el plano, su peso . La fuerza de entrada es la fuerza ejercida sobre el objeto, paralela al plano, para moverlo hacia arriba del plano. La ventaja mecánica es METRO A {\displaystyle \mathrm {MA}} F el {\displaystyle F_{\text{w}}} F i {\displaystyle F_{\text{i}}}

METRO A = F el F i {\displaystyle \mathrm {MA} ={\frac {F_{\text{w}}}{F_{\text{i}}}}\,}

La MA de un plano inclinado ideal sin fricción a veces se denomina ventaja mecánica ideal , mientras que la MA cuando se incluye fricción se denomina ventaja mecánica real . [32] METRO A {\displaystyle \mathrm {MA}} I METRO A {\displaystyle \mathrm {IMA} } A METRO A {\displaystyle \mathrm {AMA} }

Plano inclinado sin fricción

Plano inclinado instrumentado utilizado para la enseñanza de la física, alrededor de 1900. El peso de la izquierda proporciona la fuerza de carga . El peso de la derecha proporciona la fuerza de entrada que tira del rodillo hacia arriba del plano. F el {\displaystyle F_{\text{w}}} F i {\displaystyle F_{\text{i}}}

Si no hay fricción entre el objeto que se mueve y el plano, el dispositivo se denomina plano inclinado ideal . Esta condición se puede alcanzar si el objeto rueda como un barril o se apoya sobre ruedas o ruedecillas . Debido a la conservación de la energía , para un plano inclinado sin fricción, el trabajo realizado sobre la carga que lo levanta, , es igual al trabajo realizado por la fuerza de entrada, [33] [34] [35] Yo afuera {\displaystyle W_{\text{fuera}}} Yo en {\displaystyle W_{\text{en}}}

Yo o tú a = Yo i norte {\displaystyle W_{\rm {salida}}=W_{\rm {entrada}}\,}

El trabajo se define como la fuerza multiplicada por el desplazamiento que recorre un objeto. El trabajo realizado sobre la carga es igual a su peso multiplicado por el desplazamiento vertical que asciende, que es la "elevación" del plano inclinado.

Yo o tú a = F el ⋅ Elevar {\displaystyle W_{\rm {salida}}=F_{\rm {w}}\cdot {\text{Aumento}}\,}

El trabajo de entrada es igual a la fuerza sobre el objeto multiplicada por la longitud diagonal del plano inclinado. F i {\displaystyle F_{\text{i}}}

Yo i norte = F i ⋅ Longitud {\displaystyle W_{\rm {in}}=F_{\rm {i}}\cdot {\text{Longitud}}\,}

Sustituyendo estos valores en la ecuación de conservación de energía anterior y reorganizando

MAMÁ = F el F i = Longitud Elevar {\displaystyle {\text{MA}}={\frac {F_{\rm {w}}}{F_{\rm {i}}}}={\frac {\text{Longitud}}{\text{Elevación}}}\,}

Para expresar la ventaja mecánica por el ángulo del plano, [34] se puede ver en el diagrama (arriba) que θ {\estilo de visualización \theta}

pecado ⁡ θ = Elevar Longitud {\displaystyle \sin \theta ={\frac {\text{Altura}}{\text{Longitud}}}\,}

Entonces

MAMÁ = F el F i = 1 pecado ⁡ θ {\displaystyle {\text{MA}}={\frac {F_{\rm {w}}}{F_{\rm {i}}}}={\frac {1}{\sin \theta }}\,}

Por lo tanto, la ventaja mecánica de un plano inclinado sin fricción es igual al recíproco del seno del ángulo de pendiente. La fuerza de entrada de esta ecuación es la fuerza necesaria para mantener la carga inmóvil en el plano inclinado o empujarla hacia arriba a una velocidad constante. Si la fuerza de entrada es mayor que esto, la carga se acelerará hacia arriba en el plano. Si la fuerza es menor, se acelerará hacia abajo en el plano. F i {\displaystyle F_{\rm {i}}}

Plano inclinado con fricción

Cuando hay fricción entre el plano y la carga, como por ejemplo cuando una caja pesada se desliza por una rampa, parte del trabajo aplicado por la fuerza de entrada se disipa en forma de calor por fricción, por lo que se realiza menos trabajo sobre la carga. Debido a la conservación de la energía , la suma del trabajo de salida y las pérdidas de energía por fricción es igual al trabajo de entrada. Yo fricción {\displaystyle W_{\text{fric}}}

Yo en = Yo fricción + Yo afuera {\displaystyle W_{\text{entrada}}=W_{\text{fric}}+W_{\text{salida}}\,}

Por lo tanto, se requiere una mayor fuerza de entrada y la ventaja mecánica es menor que si no hubiera fricción. Con fricción, la carga solo se moverá si la fuerza neta paralela a la superficie es mayor que la fuerza de fricción que se le opone. [8] [36] [37] La ​​fuerza de fricción máxima está dada por F F {\displaystyle F_{\text{f}}}

F F = micras F norte {\displaystyle F_{f}=\mu F_{n}\,}

donde es la fuerza normal entre la carga y el plano, dirigida de forma normal a la superficie, y es el coeficiente de fricción estática entre las dos superficies, que varía con el material. Cuando no se aplica ninguna fuerza de entrada, si el ángulo de inclinación del plano es menor que un valor máximo, el componente de la fuerza gravitacional paralela al plano será demasiado pequeño para vencer la fricción, y la carga permanecerá inmóvil. Este ángulo se llama ángulo de reposo y depende de la composición de las superficies, pero es independiente del peso de la carga. A continuación se muestra que la tangente del ángulo de reposo es igual a F norte {\displaystyle F_{\text{n}}} micras {\estilo de visualización \mu} θ {\estilo de visualización \theta} ϕ {\estilo de visualización \phi} ϕ {\estilo de visualización \phi} micras {\estilo de visualización \mu}

ϕ = broncearse − 1 ⁡ micras {\displaystyle \phi =\tan ^{-1}\mu \,}

Con fricción, siempre hay un cierto rango de fuerza de entrada para el cual la carga es estacionaria, sin deslizarse hacia arriba o hacia abajo en el plano, mientras que con un plano inclinado sin fricción solo hay un valor particular de fuerza de entrada para el cual la carga es estacionaria. F i {\displaystyle F_{\text{i}}}

Análisis

Clave: F n = N = Fuerza normal que es perpendicular al plano, F i = f = fuerza de entrada, F w = mg = peso de la carga, donde m = masa , g = gravedad

Una carga que reposa sobre un plano inclinado, cuando se considera como un cuerpo libre, tiene tres fuerzas que actúan sobre ella: [8] [36] [37]

  • La fuerza aplicada, ejercida sobre la carga para moverla, que actúa paralela al plano inclinado. F i {\displaystyle F_{\text{i}}}
  • El peso de la carga, , que actúa verticalmente hacia abajo F w {\displaystyle F_{\text{w}}}
  • La fuerza que ejerce el avión sobre la carga. Se puede descomponer en dos componentes:
    • Fuerza normal del plano inclinado sobre la carga que lo soporta. Está dirigida perpendicularmente ( normal ) a la superficie. F n {\displaystyle F_{\text{n}}}
    • La fuerza de rozamiento del plano sobre la carga actúa paralela a la superficie y siempre en dirección opuesta al movimiento del objeto. Es igual a la fuerza normal multiplicada por el coeficiente de rozamiento estático μ entre las dos superficies. F f {\displaystyle F_{\text{f}}}

Si se aplica la segunda ley de movimiento de Newton, la carga estará estacionaria o en movimiento constante si la suma de las fuerzas que actúan sobre ella es cero. Como la dirección de la fuerza de fricción es opuesta para el caso del movimiento ascendente y descendente, estos dos casos deben considerarse por separado:

  • Movimiento cuesta arriba: la fuerza total sobre la carga es hacia el lado cuesta arriba, por lo que la fuerza de fricción se dirige hacia abajo del plano, oponiéndose a la fuerza de entrada.
Derivación de la ventaja mecánica para el movimiento cuesta arriba
Las ecuaciones de equilibrio para fuerzas paralelas y perpendiculares al plano son
∑ F ‖ = F i − F f − F w sin ⁡ θ = 0 {\displaystyle \sum F_{\|}=F_{i}-F_{f}-F_{w}\sin \theta =0\,}
∑ F ⊥ = F n − F w cos ⁡ θ = 0 {\displaystyle \sum F_{\perp }=F_{n}-F_{w}\cos \theta =0\,}
Sustituyendo en la primera ecuación F f = μ F n {\displaystyle F_{f}=\mu F_{n}\,}
F i − μ F n − F w sin ⁡ θ = 0 {\displaystyle F_{i}-\mu F_{n}-F_{w}\sin \theta =0\,}
Resolviendo la segunda ecuación para obtener y sustituyendo en la ecuación anterior F n = F w cos ⁡ θ {\displaystyle F_{n}=F_{w}\cos \theta \,}
F i − μ F w cos ⁡ θ − F w sin ⁡ θ = 0 {\displaystyle F_{i}-\mu F_{w}\cos \theta -F_{w}\sin \theta =0\,}
F w F i = 1 sin ⁡ θ + μ cos ⁡ θ {\displaystyle {\frac {F_{w}}{F_{i}}}={\frac {1}{\sin \theta +\mu \cos \theta }}\,}
Definiendo μ = tan ⁡ ϕ {\displaystyle \mu =\tan \phi \,}
F w F i = 1 sin ⁡ θ + tan ⁡ ϕ cos ⁡ θ = 1 sin ⁡ θ + sin ⁡ ϕ cos ⁡ ϕ cos ⁡ θ = cos ⁡ ϕ sin ⁡ θ cos ⁡ ϕ + cos ⁡ θ sin ⁡ ϕ {\displaystyle {\frac {F_{w}}{F_{i}}}={\frac {1}{\sin \theta +\tan \phi \cos \theta }}={\dfrac {1}{\sin \theta +{\dfrac {\sin \phi }{\cos \phi }}\cos \theta }}={\frac {\cos \phi }{\sin \theta \cos \phi +\cos \theta \sin \phi }}\,}
Utilizando una identidad trigonométrica de suma de ángulos en el denominador,
La ventaja mecánica es
M A = F w F i = cos ⁡ ϕ sin ⁡ ( θ + ϕ ) {\displaystyle \mathrm {MA} ={\frac {F_{w}}{F_{i}}}={\frac {\cos \phi }{\sin(\theta +\phi )}}\,}
donde . Esta es la condición para el movimiento inminente hacia arriba en el plano inclinado. Si la fuerza aplicada F i es mayor que la dada por esta ecuación, la carga se moverá hacia arriba en el plano. ϕ = tan − 1 ⁡ μ {\displaystyle \phi =\tan ^{-1}\mu \,}
  • Movimiento cuesta abajo: la fuerza total sobre la carga es hacia el lado cuesta abajo, por lo que la fuerza de fricción se dirige hacia arriba del plano.
Derivación de la ventaja mecánica para el movimiento cuesta abajo
Las ecuaciones de equilibrio son
∑ F ‖ = F i + F f − F w sin ⁡ θ = 0 {\displaystyle \sum F_{\|}=F_{i}+F_{f}-F_{w}\sin \theta =0\,}
∑ F ⊥ = F n − F w cos ⁡ θ = 0 {\displaystyle \sum F_{\perp }=F_{n}-F_{w}\cos \theta =0\,}
Sustituyendo en la primera ecuación F f = μ F n {\displaystyle F_{f}=\mu F_{n}\,}
F i + μ F n − F w sin ⁡ θ = 0 {\displaystyle F_{i}+\mu F_{n}-F_{w}\sin \theta =0\,}
Resolviendo la segunda ecuación para obtener y sustituyendo en la ecuación anterior F n = F w cos ⁡ θ {\displaystyle F_{n}=F_{w}\cos \theta \,}
F i + μ F w cos ⁡ θ − F w sin ⁡ θ = 0 {\displaystyle F_{i}+\mu F_{w}\cos \theta -F_{w}\sin \theta =0\,}
F w F i = 1 sin ⁡ θ − μ cos ⁡ θ {\displaystyle {\frac {F_{w}}{F_{i}}}={\frac {1}{\sin \theta -\mu \cos \theta }}\,}
Sustituyendo y simplificando como se indica arriba μ = tan ⁡ ϕ {\displaystyle \mu =\tan \phi \,}
F w F i = cos ⁡ ϕ sin ⁡ θ cos ⁡ ϕ − cos ⁡ θ sin ⁡ ϕ {\displaystyle {\frac {F_{w}}{F_{i}}}={\frac {\cos \phi }{\sin \theta \cos \phi -\cos \theta \sin \phi }}\,}
Usando otra identidad trigonométrica en el denominador,
La ventaja mecánica es
M A = F w F i = cos ⁡ ϕ sin ⁡ ( θ − ϕ ) {\displaystyle \mathrm {MA} ={\frac {F_{w}}{F_{i}}}={\frac {\cos \phi }{\sin(\theta -\phi )}}\,}
Esta es la condición para que se produzca un movimiento inminente hacia abajo en el plano: si la fuerza aplicada F i es menor que la indicada en esta ecuación, la carga se deslizará hacia abajo en el plano. Existen tres casos:
  1. θ < ϕ {\displaystyle \theta <\phi \,} :La ventaja mecánica es negativa. Si no se aplica ninguna fuerza, la carga permanecerá inmóvil y se requiere aplicar alguna fuerza negativa (cuesta abajo) para deslizarse hacia abajo.
  2. θ = ϕ {\displaystyle \theta =\phi \,} :El " ángulo de reposo ". La ventaja mecánica es infinita. Sin fuerza aplicada, la carga no se deslizará, pero la más mínima fuerza negativa (cuesta abajo) hará que se deslice.
  3. θ > ϕ {\displaystyle \theta >\phi \,} :La ventaja mecánica es positiva. En ausencia de fuerza aplicada, la carga se deslizará hacia abajo del plano y se requiere cierta fuerza positiva (cuesta arriba) para mantenerla inmóvil.

Ventaja mecánica usando potencia

Clave: N = Fuerza normal que es perpendicular al plano, W=mg, donde m = masa , g = gravedad y θ ( theta ) = Ángulo de inclinación del plano

La ventaja mecánica de un plano inclinado es la relación entre el peso de la carga sobre la rampa y la fuerza necesaria para subirla por ella. Si no se disipa ni se almacena energía en el movimiento de la carga, esta ventaja mecánica se puede calcular a partir de las dimensiones de la rampa.

Para demostrar esto, sea la posición r de un vagón de ferrocarril a lo largo de la rampa con un ángulo θ , por encima de la horizontal dada por

r = R ( cos ⁡ θ , sin ⁡ θ ) , {\displaystyle \mathbf {r} =R(\cos \theta ,\sin \theta ),}

donde R es la distancia a lo largo de la rampa. La velocidad del automóvil en la rampa es ahora

v = V ( cos ⁡ θ , sin ⁡ θ ) . {\displaystyle \mathbf {v} =V(\cos \theta ,\sin \theta ).}

Como no hay pérdidas, la potencia utilizada por la fuerza F para mover la carga por la rampa es igual a la potencia de salida, que es la elevación vertical del peso W de la carga.

La potencia de entrada que impulsa el automóvil por la rampa está dada por

P i n = F V , {\displaystyle P_{\mathrm {in} }=FV,\!}

y se apaga la luz

P o u t = W ⋅ v = ( 0 , W ) ⋅ V ( cos ⁡ θ , sin ⁡ θ ) = W V sin ⁡ θ . {\displaystyle P_{\mathrm {out} }=\mathbf {W} \cdot \mathbf {v} =(0,W)\cdot V(\cos \theta ,\sin \theta )=WV\sin \theta .}

Iguale la potencia de entrada con la potencia de salida para obtener la ventaja mecánica como

M A = W F = 1 sin ⁡ θ . {\displaystyle \mathrm {MA} ={\frac {W}{F}}={\frac {1}{\sin \theta }}.}

La ventaja mecánica de un plano inclinado también se puede calcular a partir de la relación entre la longitud de la rampa L y su altura H, porque el seno del ángulo de la rampa viene dado por

sin ⁡ θ = H L , {\displaystyle \sin \theta ={\frac {H}{L}},}

por lo tanto,

M A = W F = L H . {\displaystyle \mathrm {MA} ={\frac {W}{F}}={\frac {L}{H}}.}
Disposición del sistema de accionamiento por cable para el plano inclinado Liverpool Minard.

Ejemplo: Si la altura de una rampa es H = 1 metro y su longitud es L = 5 metros, entonces la ventaja mecánica es

M A = W F = 5 , {\displaystyle \mathrm {MA} ={\frac {W}{F}}=5,}

lo que significa que una fuerza de 20 libras levantará una carga de 100 libras.

El plano inclinado Liverpool Minard tiene unas dimensiones de 1804 metros por 37,50 metros, lo que proporciona una ventaja mecánica de

M A = W F = 1804 / 37.50 = 48.1 , {\displaystyle \mathrm {MA} ={\frac {W}{F}}=1804/37.50=48.1,}

Por lo tanto, una fuerza de tensión de 100 lb sobre el cable levantará una carga de 4810 lb. La pendiente de esta inclinación es del 2 %, lo que significa que el ángulo θ es lo suficientemente pequeño como para que sen θ ≈ tan θ.

Véase también

Referencias

  1. ^ ab Cole, Matthew (2005). Explore Science, 2.ª edición, Pearson Education, pág. 178. ISBN 978-981-06-2002-8.
  2. ^ Diccionario colegiado de Merriam-Webster, 11.ª edición . Merriam-Webster. 2003. págs. 629. ISBN 978-0-87779-809-5Diccionario de definiciones de plano inclinado .
  3. ^ abcd "El plano inclinado". Centro de actividades de matemáticas y ciencias . Edinformatics. 1999. Consultado el 11 de marzo de 2012 .
  4. ^ abc Silverman, Buffy (2009). Máquinas simples: fuerzas en acción, 4.ª ed. EE. UU.: Heinemann-Raintree Classroom. pág. 7. ISBN 978-1-4329-2317-4.
  5. ^ abc Ortleb, Edward P.; Richard Cadice (1993). Máquinas y trabajo. Lorenz Educational Press. pp. iv. ISBN 978-1-55863-060-4.
  6. ^ ab Reilly, Travis (24 de noviembre de 2011). "Lección 04: Deslizarse hacia la derecha usando un plano inclinado". Teach Engineering . Facultad de Ingeniería, Universidad de Colorado en Boulder. Archivado desde el original el 8 de mayo de 2012 . Consultado el 8 de septiembre de 2012 .
  7. ^ Scott, John S. (1993). Diccionario de ingeniería civil. Chapman & Hill. pág. 14. ISBN 978-0-412-98421-1. ángulo de fricción [mec.] en el estudio de cuerpos que se deslizan sobre superficies planas, el ángulo entre la perpendicular a la superficie y la fuerza resultante (entre el cuerpo y la superficie) cuando el cuerpo comienza a deslizarse. ángulo de reposo [sm] para cualquier material granular dado el ángulo más pronunciado con la horizontal en el que una superficie apilada permanecerá en condiciones determinadas.
  8. ^ abcd Ambekar, AG (2007). Mecanismo y teoría de máquinas. PHI Learning. pág. 446. ISBN 978-81-203-3134-1El ángulo de reposo es el ángulo límite de inclinación de un plano cuando un cuerpo, colocado sobre el plano inclinado, apenas comienza a deslizarse hacia abajo por el plano .
  9. ^ Rosen, Joe; Lisa Quinn Gothard (2009). Enciclopedia de ciencias físicas, volumen 1. Infobase Publishing. pág. 375. ISBN 978-0-8160-7011-4.
  10. ^ abc Koetsier, Teun (2010). "Simon Stevin y el surgimiento de la mecánica de Arquímedes en el Renacimiento". El genio de Arquímedes: 23 siglos de influencia en las matemáticas, la ciencia y la ingeniería: Actas de una conferencia internacional celebrada en Siracusa, Italia, del 8 al 10 de junio de 2010. Springer. págs. 94–99. ISBN 978-90-481-9090-4.
  11. ^ Devreese, Jozef T.; Guido Vanden Berghe (2008). 'La magia no es magia': El maravilloso mundo de Simon Stevin. WIT Press. pp. 136–139. ISBN 978-1-84564-391-1.
  12. ^ ab Feynman, Richard P.; Robert B. Leighton; Matthew Sands (1963). Las conferencias Feynman sobre física, vol. I. EE. UU.: Instituto Tecnológico de California. págs. 4.4-4.5. ISBN 978-0-465-02493-3.
  13. ^ EJDijksterhuis: Simon Stevin 1943
  14. ^ Therese McGuire, Light on Sacred Stones (Luz sobre las piedras sagradas) , en Conn, Marie A.; Therese Benedict McGuire (2007). Not grabado en piedra: ensayos sobre la memoria ritual, el alma y la sociedad. University Press of America. pág. 23. ISBN 978-0-7618-3702-2.
  15. ^ Dutch, Steven (1999). "Pre-Greek Accomplishments". Legacy of the Ancient World . Página del profesor Steve Dutch, Universidad de Wisconsin en Green Bay. Archivado desde el original el 21 de agosto de 2016. Consultado el 13 de marzo de 2012 .
  16. ^ Moffett, Marian; Michael W. Fazio; Lawrence Wodehouse (2003). Una historia mundial de la arquitectura. Laurence King Publishing. pág. 9. ISBN 978-1-85669-371-4.
  17. ^ Peet, T. Eric (2006). Monumentos de piedra tosca y sus constructores. Echo Library. págs. 11-12. ISBN 978-1-4068-2203-8.
  18. ^ Thomas, Burke (2005). "Transporte y plano inclinado". Construcción de las pirámides de Giza . world-mysteries.com. Archivado desde el original el 13 de marzo de 2012. Consultado el 10 de marzo de 2012 .
  19. ^ Isler, Martin (2001). Palos, piedras y sombras: la construcción de las pirámides egipcias . Estados Unidos: University of Oklahoma Press. pp. 211–216. ISBN 978-0-8061-3342-3.
  20. ^ Sprague de Camp, L. (1990). Los ingenieros antiguos. Estados Unidos: Barnes & Noble. pág. 43. ISBN 978-0-88029-456-0.
  21. ^ de Karl von Langsdorf (1826) Machinenkunde , citado en Reuleaux, Franz (1876). La cinemática de la maquinaria: Esbozos de una teoría de las máquinas. MacMillan. págs. 604.
  22. ^ Por ejemplo, las listas de máquinas simples que dejaron el arquitecto romano Vitruvio (c. 80-15 a. C.) y el filósofo griego Herón de Alejandría (c. 10-70 d. C.) constan de las cinco máquinas simples clásicas, excluyendo el plano inclinado. – Smith, William (1848). Dictionary of Greek and Roman antiquities. Londres: Walton and Maberly; John Murray. pág. 722.Usher , Abbott Payson (1988). Una historia de las invenciones mecánicas. Estados Unidos: Courier Dover Publications. pp. 98, 120. ISBN. 978-0-486-25593-4.
  23. ^ Heath, Thomas Little (1921). Una historia de las matemáticas griegas, vol. 2. Reino Unido: The Clarendon Press. págs. 349, 433–434.
  24. ^ abc Egidio Festa y Sophie Roux , El enigma del plano inclinado en Laird, Walter Roy; Sophie Roux (2008). Mecánica y filosofía natural antes de la revolución científica. Estados Unidos: Springer. pp. 195–221. ISBN 978-1-4020-5966-7.
  25. ^ ab Meli, Domenico Bertoloni (2006). Pensar con objetos: la transformación de la mecánica en el siglo XVII. JHU Press. pp. 35–39. ISBN 978-0-8018-8426-9.
  26. ^ de Boyer, Carl B.; Uta C. Merzbach (2010). Una historia de las matemáticas, 3.ª edición. John Wiley and Sons. ISBN 978-0-470-63056-3.
  27. ^ Usher, Abbott Payson (1988). Una historia de las invenciones mecánicas. Courier Dover Publications. pág. 106. ISBN 978-0-486-25593-4.
  28. ^ Machamer, Peter K. (1998). The Cambridge Companion to Galileo. Londres: Cambridge University Press. pp. 47–48. ISBN 978-0-521-58841-6.
  29. ^ ab Armstrong-Hélouvry, Brian (1991). Control de máquinas por fricción. EE.UU.: Springer. p. 10. ISBN 978-0-7923-9133-3.
  30. ^ Meyer, Ernst (2002). Nanociencia: fricción y reología a escala nanométrica. World Scientific. pág. 7. ISBN 978-981-238-062-3.
  31. ^ ab Handley, Brett; David M. Marshall; Craig Coon (2011). Principios de ingeniería. Cengage Learning. págs. 71–73. ISBN 978-1-4354-2836-2.
  32. ^ Dennis, Johnnie T. (2003). Guía completa de física para idiotas. Penguin. pp. 116-117. ISBN 978-1-59257-081-2.
  33. ^ Nave, Carl R. (2010). "The Incline". Hiperfísica . Departamento de Física y Astronomía, Universidad Estatal de Georgia . Consultado el 8 de septiembre de 2012 .
  34. ^ ab Martin, Lori (2010). "Lab Mech14: The Inclined Plane - A Simple Machine" (PDF) . Science in Motion . Westminster College . Consultado el 8 de septiembre de 2012 .
  35. ^ Pearson (2009). Física, clase 10. Serie de fundamentos del IIT. Nueva Delhi: Pearson Education India. pág. 69. ISBN 978-81-317-2843-7.
  36. ^ ab Bansal, RK (2005). Mecánica de ingeniería y resistencia de materiales. Laxmi Publications. págs. 165-167. ISBN 978-81-7008-094-7.
  37. ^ ab Esto deriva en ecuaciones ligeramente más generales que cubren la fuerza aplicada en cualquier ángulo: Gujral, IS (2008). Ingeniería mecánica. Firewall Media. pp. 275–277. ISBN 978-81-318-0295-3.
Wikimedia Commons alberga una categoría multimedia sobre Planos inclinados .
  • Una simulación interactiva del plano inclinado de Física
Retrieved from "https://en.wikipedia.org/w/index.php?title=Inclined_plane&oldid=1229154611"