Diámetro angular
Este artículo necesita citas adicionales para su verificación . ( septiembre de 2009 ) |
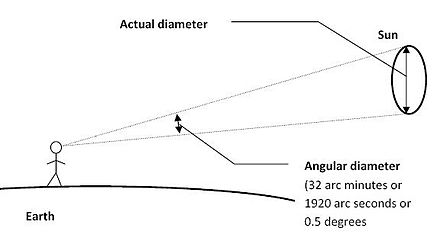
El diámetro angular , tamaño angular , diámetro aparente o tamaño aparente es una distancia angular que describe cuán grande parece una esfera o un círculo desde un punto de vista determinado. En las ciencias de la visión , se denomina ángulo visual y, en óptica , es la apertura angular (de una lente ). El diámetro angular también se puede considerar como el desplazamiento angular a través del cual un ojo o una cámara deben rotar para mirar desde un lado de un círculo aparente al lado opuesto. Los humanos pueden resolver con sus ojos desnudos diámetros de hasta aproximadamente 1 minuto de arco (aproximadamente 0,017° o 0,0003 radianes). [1] Esto corresponde a 0,3 m a una distancia de 1 km, o a percibir Venus como un disco en condiciones óptimas.
Fórmula

El diámetro angular de un círculo cuyo plano es perpendicular al vector de desplazamiento entre el punto de vista y el centro de dicho círculo se puede calcular mediante la fórmula [2] [3]
donde es el diámetro angular en grados , y es el diámetro real del objeto, y es la distancia al objeto. Cuando , tenemos , [4] y el resultado obtenido está en radianes .
Para un objeto esférico cuyo diámetro real es igual a y donde es la distancia al centro de la esfera, el diámetro angular se puede encontrar mediante la siguiente fórmula modificada [ cita requerida ]
La diferencia se debe a que los bordes aparentes de una esfera son sus puntos tangentes, que están más cerca del observador que el centro de la esfera y tienen una distancia entre ellos que es menor que el diámetro real. La fórmula anterior se puede encontrar entendiendo que en el caso de un objeto esférico, se puede construir un triángulo rectángulo de modo que sus tres vértices sean el observador, el centro de la esfera y uno de los puntos tangentes de la esfera, con como hipotenusa y como seno. [ cita requerida ]
La diferencia es significativa sólo para objetos esféricos de gran diámetro angular, ya que las siguientes aproximaciones de ángulos pequeños son válidas para valores pequeños de : [5]
Estimación del diámetro angular usando la mano

Se pueden obtener estimaciones del diámetro angular sosteniendo la mano en ángulo recto con el brazo completamente extendido , como se muestra en la figura. [6] [7] [8]
Uso en astronomía
.jpg/440px-thumbnail.jpg)
En astronomía , los tamaños de los objetos celestes se dan a menudo en términos de su diámetro angular visto desde la Tierra , en lugar de sus tamaños reales. Dado que estos diámetros angulares son típicamente pequeños, es común presentarlos en segundos de arco (″). Un segundo de arco es 1/3600 de un grado (1°) y un radián es 180/ π grados. Por lo tanto, un radián equivale a 3600 × 180/ segundos de arco, que son aproximadamente 206 265 segundos de arco (1 rad ≈ 206 264,806247"). Por lo tanto, el diámetro angular de un objeto con diámetro físico d a una distancia D , expresado en segundos de arco, viene dado por: [9]
- .
Estos objetos tienen un diámetro angular de 1″:
- un objeto de 1 cm de diámetro a una distancia de 2,06 km
- un objeto de diámetro 725,27 km a una distancia de 1 unidad astronómica (UA)
- un objeto de diámetro 45 866 916 km a 1 año luz
- un objeto de diámetro 1 UA (149 597 871 km) a una distancia de 1 parsec (pc)
Por lo tanto, el diámetro angular de la órbita de la Tierra alrededor del Sol visto desde una distancia de 1 pc es 2″, ya que 1 UA es el radio medio de la órbita de la Tierra.
El diámetro angular del Sol, desde una distancia de un año luz , es de 0,03″, y el de la Tierra, de 0,0003″. El diámetro angular de 0,03″ del Sol indicado anteriormente es aproximadamente el mismo que el de un cuerpo humano a una distancia del diámetro de la Tierra.
Esta tabla muestra los tamaños angulares de cuerpos celestes notables vistos desde la Tierra:
| Objeto celeste | Diámetro o tamaño angular | Tamaño relativo |
|---|---|---|
| Corriente de Magallanes | Más de 100° | |
| Nebulosa de la goma | 36° | |
| vía Láctea | 30° (por 360°) | |
| Ancho de la mano extendida con el brazo estirado | 20° | 353 metros a 1 km de distancia |
| Grieta Serpens-Aquila | 20° por 10° | |
| Sobredensidad del can mayor | 12° por 12° | |
| La nube de Smith | 11° | |
| Gran Nube de Magallanes | 10,75° por 9,17° | Nota: la galaxia más brillante , aparte de la Vía Láctea, en el cielo nocturno ( magnitud aparente (V) 0,9 ) |
| El bucle de Barnard | 10° | |
| Nebulosa Zeta Ophiuchi Sh2-27 | 10° | |
| Ancho del puño con el brazo estirado | 10° | 175 metros a 1 km de distancia |
| Galaxia enana esferoidal de Sagitario | 7,5° por 3,6° | |
| Nebulosa Saco de Carbón del Norte | 7° por 5° [10] | |
| Nebulosa del saco de carbón | 7° por 5° | |
| Cisne OB7 | 4° por 7° [11] | |
| Complejo de nubes Rho Ophiuchi | 4,5° por 6,5° | |
| Híades | 5°30 ′ | Nota: cúmulo estelar más brillante del cielo nocturno, magnitud aparente (V) 0,5 |
| Pequeña Nube de Magallanes | 5°20 ′ por 3°5 ′ | |
| Galaxia de Andrómeda | 3°10 ′ por 1° | Aproximadamente seis veces el tamaño del Sol o la Luna. Solo el núcleo, mucho más pequeño, es visible sin necesidad de fotografías de larga exposición . |
| Caronte (desde la superficie de Plutón ) | 3°9' | |
| Nebulosa del Velo | 3° | |
| Nebulosa del corazón | 2,5° por 2,5° | |
| Westerhout 5 | 2,3° por 1,25° | |
| Sh2-54 | 2,3° | |
| Nebulosa Carina | 2° por 2° | Nota: nebulosa más brillante del cielo nocturno, magnitud aparente (V) 1,0 |
| Nebulosa de América del Norte | 2° por 100 ′ | |
| La Tierra en el cielo de la Luna | 2° - 1°48 ′ [12] | Aparece aproximadamente tres o cuatro veces más grande que la Luna en el cielo de la Tierra. |
| El Sol en el cielo de Mercurio | 1,15° - 1,76° | [13] |
| Nebulosa de Orión | 1°5 ′ por 1° | |
| Ancho del dedo meñique con el brazo estirado | 1° | 17,5 metros a 1 km de distancia |
| El Sol en el cielo de Venus | 0,7° | [13] [14] |
| Ío (visto desde la “superficie” de Júpiter) | 35' 35” | |
| Luna | 34 ′ 6″ – 29 ′ 20″ | 32,5–28 veces el valor máximo de Venus (barra naranja a continuación) / 2046–1760″ la Luna tiene un diámetro de 3.474 km |
| Sol | 32 ′ 32″ – 31 ′ 27″ | 31–30 veces el valor máximo de Venus (barra naranja a continuación) / 1952–1887″ el Sol tiene un diámetro de 1.391.400 km |
| Tritón (desde la “superficie” de Neptuno) | 28' 11” | |
| Tamaño angular de la distancia entre la Tierra y la Luna vista desde Marte , en conjunción inferior | unos 25 ′ | |
| Ariel (desde la “superficie” de Urano) | 24' 11” | |
| Ganimedes (desde la “superficie” de Júpiter) | 18' 6” | |
| Europa (desde la “superficie” de Júpiter) | 17' 51” | |
| Umbriel (de la “superficie” de Urano) | 16' 42” | |
| Nebulosa de la hélice | aproximadamente 16 ′ por 28 ′ | |
| Júpiter si estuviera tan cerca de la Tierra como Marte | 9,0 ′ – 1,2 ′ | |
| Aguja en la Nebulosa del Águila | 4 ′ 40″ | La longitud es de 280″ |
| Fobos visto desde Marte | 4.1 ′ | |
| Venus | 1 ′ 6″ – 0 ′ 9.7″ | |
| Estación Espacial Internacional (ISS) | 1 ′ 3″ | [15] La ISS tiene un ancho de unos 108 m. |
| Diámetro mínimo resoluble por el ojo humano | 1 ′ | [16] 0,3 metros a 1 km de distancia [17]
|
| A unos 100 km de la superficie de la Luna | 1 ′ | Comparable en tamaño a características como los grandes cráteres lunares, como el cráter Copérnico , un punto brillante prominente en la parte oriental del Oceanus Procellarum en el lado menguante, o el cráter Tycho dentro de un área brillante en el sur del lado cercano de la Luna . |
| Júpiter | 50,1″ – 29,8″ | |
| La Tierra vista desde Marte | 48,2″ [13] – 6,6″ | |
| Mínimo espacio resoluble entre dos líneas por el ojo humano | 40″ | un espacio de 0,026 mm visto desde una distancia de 15 cm [16] [17] |
| Marte | 25,1″ – 3,5″ | |
| Tamaño aparente del Sol, visto desde 90377 Sedna en el afelio | 20,4" | |
| Saturno | 20,1″ – 14,5″ | |
| Mercurio | 13,0″ – 4,5″ | |
| La Luna de la Tierra vista desde Marte | 13,27″ – 1,79″ | |
| Urano | 4,1″ – 3,3″ | |
| Neptuno | 2,4″ – 2,2″ | |
| Ganimedes | 1,8″ – 1,2″ | Ganimedes tiene un diámetro de 5.268 km. |
| Un astronauta (~1,7 m) a una distancia de 350 km, la altitud media de la ISS | 1″ | |
| Diámetro mínimo resoluble por los telescopios refractores más grandes de 38 mm de Galileo Galilei | ~1″ | [18] Nota: aumento de 30x [19] , comparable a binoculares terrestres contemporáneos muy potentes |
| Ceres | 0,84″ – 0,33″ | |
| Vesta | 0,64″ – 0,20″ | |
| Plutón | 0,11″ – 0,06″ | |
| Eris | 0,089″ – 0,034″ | |
| R Dorado | 0,062″ – 0,052″ | Nota: Se cree que R Doradus es la estrella extrasolar con el mayor tamaño aparente visto desde la Tierra. |
| Betelgeuse | 0,060″ – 0,049″ | |
| Alfard | 0,00909″ | |
| Alfa Centauri A | 0,007″ | |
| Canopo | 0,006″ | |
| Sirio | 0,005936″ | |
| Altair | 0,003″ | |
| Rho Casiopea | 0,0021″ [20] | |
| Deneb | 0,002″ | |
| Próxima Centauri | 0,001″ | |
| Alnitak | 0,0005″ | |
| Próxima Centauri b | 0,00008″ | |
| Horizonte de sucesos del agujero negro M87* en el centro de la galaxia M87, fotografiado por el Event Horizon Telescope en 2019. | 0,000025″ (2,5 × 10 −5 ) | Comparable a una pelota de tenis en la Luna |
| Una estrella como Alnitak a una distancia donde el telescopio espacial Hubble apenas podría verla [21] | 6 × 10 −10 segundos de arco |



El diámetro angular del Sol, visto desde la Tierra, es aproximadamente 250.000 veces el de Sirio . (Sirio tiene el doble de diámetro y su distancia es 500.000 veces mayor; el Sol es 10 10 veces más brillante, lo que corresponde a una relación de diámetro angular de 10 5 , por lo que Sirio es aproximadamente 6 veces más brillante por unidad de ángulo sólido .)
El diámetro angular del Sol también es aproximadamente 250.000 veces el de Alfa Centauri A (tiene aproximadamente el mismo diámetro y la distancia es 250.000 veces mayor; el Sol es 4×10 10 veces más brillante, lo que corresponde a una relación de diámetro angular de 200.000, por lo que Alfa Centauri A es un poco más brillante por unidad de ángulo sólido).
El diámetro angular del Sol es aproximadamente el mismo que el de la Luna . (El diámetro del Sol es 400 veces mayor y su distancia también; el Sol es entre 200.000 y 500.000 veces más brillante que la Luna llena (las cifras varían), lo que corresponde a una relación de diámetro angular de 450 a 700, por lo que un cuerpo celeste con un diámetro de 2,5–4″ y el mismo brillo por unidad de ángulo sólido tendría el mismo brillo que la Luna llena).
Aunque Plutón es físicamente más grande que Ceres, cuando se lo observa desde la Tierra (por ejemplo, a través del telescopio espacial Hubble ) Ceres tiene un tamaño aparente mucho mayor.
Los tamaños angulares medidos en grados son útiles para áreas más grandes del cielo. (Por ejemplo, las tres estrellas del Cinturón cubren aproximadamente 4,5° de tamaño angular). Sin embargo, se necesitan unidades mucho más precisas para medir los tamaños angulares de galaxias, nebulosas u otros objetos del cielo nocturno .
Los grados, por tanto, se subdividen de la siguiente manera:
- 360 grados (°) en un círculo completo
- 60 minutos de arco ( ′ ) en un grado
- 60 segundos de arco (″) en un minuto de arco
Para poner esto en perspectiva, la Luna llena vista desde la Tierra tiene un ángulo de aproximadamente 1 ⁄ 2 °, o 30 ′ (o 1800″). El movimiento de la Luna a través del cielo se puede medir en tamaño angular: aproximadamente 15° cada hora, o 15″ por segundo. Una línea de una milla de largo pintada en la cara de la Luna parecería desde la Tierra tener aproximadamente 1″ de longitud.
En astronomía, suele ser difícil medir directamente la distancia a un objeto, aunque el objeto puede tener un tamaño físico conocido (quizás es similar a un objeto más cercano con una distancia conocida) y un diámetro angular medible. En ese caso, la fórmula del diámetro angular se puede invertir para obtener la distancia del diámetro angular a objetos distantes como
En el espacio no euclidiano, como nuestro universo en expansión, la distancia del diámetro angular es solo una de varias definiciones de distancia, de modo que puede haber diferentes "distancias" al mismo objeto. Véase Medidas de distancia (cosmología) .
Objetos no circulares
Muchos objetos del cielo profundo, como las galaxias y las nebulosas, parecen no circulares y, por lo tanto, se les asignan dos medidas de diámetro: eje mayor y eje menor. Por ejemplo, la Pequeña Nube de Magallanes tiene un diámetro visual aparente de 5° 20′ × 3° 5′.
Defecto de iluminación
El defecto de iluminación es el ancho angular máximo de la parte no iluminada de un cuerpo celeste que ve un observador determinado. Por ejemplo, si un objeto tiene un arco de 40″ de ancho y está iluminado en un 75 %, el defecto de iluminación es de 10″.
Véase también
- Distancia de diámetro angular
- Resolución angular
- Angulo solido
- Agudeza visual
- Angulo visual
- Ángulo visual percibido
- Lista de estrellas con imágenes resueltas
- Magnitud aparente
Referencias
- ^ Yanoff, Myron; Duker, Jay S. (2009). Oftalmología, 3.ª edición. MOSBY Elsevier. pág. 54. ISBN 978-0444511416.
- ^ Esto se puede obtener utilizando la fórmula para la longitud de una cuerda que se encuentra en "Segmento circular". Archivado desde el original el 21 de diciembre de 2014. Consultado el 23 de enero de 2015 .
- ^ "Diámetro angular | Repositorio de fórmulas de Wolfram". resources.wolframcloud.com . Consultado el 10 de abril de 2024 .
- ^ "Notas 7A: Tamaño angular/Distancia y áreas" (PDF) .
- ^ "Una serie de Taylor para el funcionarco" (PDF) . Archivado desde el original (PDF) el 18 de febrero de 2015. Consultado el 23 de enero de 2015 .
- ^ "Sistemas de coordenadas". Archivado desde el original el 21 de enero de 2015. Consultado el 21 de enero de 2015 .
- ^ "Fotografiando satélites". 8 de junio de 2013. Archivado desde el original el 21 de enero de 2015.
- ^ Wikiversidad: Laboratorios de Física y Astronomía/Tamaño angular
- ^ Michael A. Seeds; Dana E. Backman (2010). Estrellas y galaxias (7.ª ed.). Brooks Cole. pág. 39. ISBN 978-0-538-73317-5.
- ^ O'Meara, Stephen James (6 de agosto de 2019). "Los sacos de carbón de Cygnus". Astronomy.com . Consultado el 10 de febrero de 2023 .
- ^ Dobashi, Kazuhito; Matsumoto, Tomoaki; Shimoikura, Tomomi; Saito, Hiro; Akisato, Ko; Ohashi, Kenjiro; Nakagomi, Keisuke (24 de noviembre de 2014). "Filamentos en colisión y un núcleo denso masivo en la nube molecular Cygnus Ob 7". La revista astrofísica . 797 (1). Sociedad Astronómica Estadounidense: 58. arXiv : 1411.0942 . Código Bib : 2014ApJ...797...58D. doi :10.1088/0004-637x/797/1/58. ISSN 1538-4357. S2CID 118369651.
- ^ Gorkavyi, Nick; Krotkov, Nickolay; Marshak, Alexander (24 de marzo de 2023). "Observaciones de la Tierra desde la superficie de la Luna: dependencia de la libración lunar". Técnicas de medición atmosférica . 16 (6). Copernicus GmbH: 1527–1537. Bibcode :2023AMT....16.1527G. doi : 10.5194/amt-16-1527-2023 . ISSN 1867-8548.
- ^ abc "El Sol y los tránsitos vistos desde los planetas". RASC Calgary Centre . 2018-11-05 . Consultado el 2024-08-23 .
- ^ "¿Qué tan grande se ve el Sol desde Mercurio y Venus, en comparación con cómo lo vemos desde la Tierra?". Revista Astronomy . 2018-05-31 . Consultado el 2024-08-23 .
- ^ "Problema 346: La Estación Espacial Internacional y una mancha solar: exploración de escalas angulares" (PDF) . Matemáticas espaciales @ NASA ! . 2018-08-19 . Consultado el 2022-05-20 .
- ^ ab Wong, Yan (24 de enero de 2016). "¿Qué tan pequeño puede ver el ojo desnudo?". BBC Science Focus Magazine . Consultado el 23 de mayo de 2022 .
- ^ ab "Ojos agudos: ¿qué tan bien podemos ver realmente?". Science in School – scienceinschool.org . 2016-09-07 . Consultado el 2022-05-23 .
- ^ Graney, Christopher M. (10 de diciembre de 2006). "La precisión de las observaciones de Galileo y la búsqueda temprana de paralaje estelar". arXiv : physics/0612086 . doi :10.1007/3-540-50906-2_2.
{{cite journal}}: Requiere citar revista|journal=( ayuda ) - ^ "El telescopio de Galileo: cómo funciona". Esposizioni on-line - Istituto e Museo di Storia della Scienza (en italiano) . Consultado el 21 de mayo de 2022 .
- ^ Anugu, Narsireddy; Baron, Fabien; Monnier, John D.; Gies, Douglas R.; Roettenbacher, Rachael M.; Schaefer, Gail H.; Montargès, Miguel; Kraus, Stefan; Bouquin, Jean-Baptiste Le (5 de agosto de 2024). "Imágenes de infrarrojo cercano de CHARA de la estrella hipergigante amarilla $\rho$ Cassiopeiae: células de convección y envoltura circunestelar". arXiv.org . Consultado el 12 de agosto de 2024 .
- ^ Su diámetro angular es 800 000 veces menor que el de Alnitak visto desde la Tierra. Alnitak es una estrella azul, por lo que emite mucha luz para su tamaño. Si estuviera 800 000 veces más lejos, su magnitud sería 31,5, el límite de lo que el Hubble puede ver.
Enlaces externos
- Fórmula de ángulo pequeño (archivada el 7 de octubre de 1997)
- Ayuda visual para el tamaño aparente de los planetas





















