Politopo integral

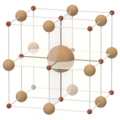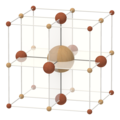Cubo	Cuboctaedro	Octaedro	Octaedro truncado
(±1, ±1, ±1)	(0, ±1, ±1)	(0, 0, ±1)	(0, ±1, ±2)
Cuatro politopos integrales en tres dimensiones

En geometría y combinatoria poliédrica , un politopo integral es un politopo convexo cuyos vértices tienen todos coordenadas cartesianas enteras . ^[1] Es decir, es un politopo que es igual a la envoltura convexa de sus puntos enteros . ^[2] Los politopos integrales también se denominan politopos reticulares o politopos Z. Los casos especiales de politopos integrales bidimensionales y tridimensionales pueden denominarse polígonos o poliedros en lugar de politopos, respectivamente.

Un símplex regular -dimensional puede representarse como un politopo entero en , la envoltura convexa de los puntos enteros para los cuales una coordenada es uno y el resto son cero. ^{[ cita requerida ]} Otro tipo importante de símplex integral, el ortosquema , puede formarse como la envoltura convexa de puntos enteros cuyas coordenadas comienzan con algún número de unos consecutivos seguidos de ceros en todas las coordenadas restantes. El cubo unitario -dimensional en tiene como vértices todos los puntos enteros cuyas coordenadas son cero o uno. Un permutaedro tiene vértices cuyas coordenadas se obtienen aplicando todas las permutaciones posibles al vector . Un asociaedro en la realización convexa de Loday es también un politopo entero y una deformación del permutaedro.${\estilo de visualización n}$${\displaystyle \mathbb {R} ^{n+1}}$${\estilo de visualización n}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle (1,2,...,n)}$

En el contexto de la programación lineal y los problemas relacionados con la optimización matemática , los politopos convexos suelen describirse mediante un sistema de desigualdades lineales que sus puntos deben obedecer. Cuando un politopo es integral, se puede utilizar la programación lineal para resolver problemas de programación entera para el sistema de desigualdades dado, un problema que de otro modo puede ser más difícil.

Algunos poliedros que surgen de problemas de optimización combinatoria son automáticamente integrales. Por ejemplo, esto es cierto para el politopo de orden de cualquier conjunto parcialmente ordenado , un politopo definido por desigualdades por pares entre coordenadas correspondientes a elementos comparables en el conjunto. ^[3] Otro politopo bien conocido en optimización combinatoria es el politopo de emparejamiento . Claramente, uno busca encontrar emparejamientos algorítmicamente y una técnica es la programación lineal. El politopo descrito por el programa lineal que limita superiormente la suma de aristas tomadas por vértice es integral en el caso de grafos bipartitos , es decir, describe exactamente el politopo de emparejamiento, mientras que para grafos generales es no integral. ^[4] Por lo tanto, para grafos bipartitos, basta con resolver el programa lineal correspondiente para obtener un emparejamiento válido . Para grafos generales, sin embargo, hay otras dos caracterizaciones del politopo de emparejamiento, una de las cuales hace uso de la desigualdad de Blossom para subconjuntos impares de vértices y, por lo tanto, permite relajar el programa entero a un programa lineal mientras se obtienen emparejamientos válidos. ^[5] Estas caracterizaciones son de mayor interés en el famoso algoritmo Blossom de Edmonds utilizado para encontrar dichas correspondencias en gráficos generales.

En el caso de un politopo descrito por desigualdades lineales, cuando el politopo no es integral, se puede demostrar su falta de integralidad hallando un vértice cuyas coordenadas no sean números enteros. Dicho vértice se puede describir de forma combinatoria especificando un subconjunto de desigualdades que, al convertirse en un sistema de ecuaciones lineales , tienen una solución única, y verificando que este punto de solución obedece a todas las demás desigualdades. Por lo tanto, la comprobación de la integralidad pertenece a la clase de complejidad coNP de problemas para los que se puede demostrar fácilmente una respuesta negativa. Más específicamente, es coNP-completo . ^[6]

Muchas de las propiedades importantes de un politopo integral, incluido su volumen y número de vértices, están codificadas por su polinomio de Ehrhart . ^[7]

Los politopos integrales ocupan un lugar destacado en la teoría de variedades tóricas , donde corresponden a variedades tóricas proyectivas polarizadas. Por ejemplo, la variedad tórica correspondiente a un símplex es un espacio proyectivo . La variedad tórica correspondiente a un cubo unitario es la incrustación de Segre del producto de pliegues de la línea proyectiva. ^{[ cita requerida ]}${\estilo de visualización n}$

En geometría algebraica , un ejemplo importante de politopos reticulares llamados politopos de Newton son las envolturas convexas de vectores que representan los exponentes de cada variable en los términos de un polinomio . Por ejemplo, el polinomio tiene cuatro términos, con vector exponente (1,1), con vector exponente (2,0), con vector exponente (0,5) y con vector exponente (0,0). Su politopo de Newton es la envoltura convexa de los cuatro puntos (1,1), (2,0), (0,5) y (0,0). Esta envoltura es un triángulo integral con el punto (1,1) interior al triángulo y los otros tres puntos como sus vértices.$Estilo de visualización xy+2x^{2}+y^{5}+4}$${\estilo de visualización xy}$$Estilo de visualización 2x^{2}}$${\displaystyle y^{5}}$${\estilo de visualización 4}$

• Politopo de Delzant
• Tetraedro de Reeve