Politopo semirregular

Las cifras de Gosset

Panales 3D
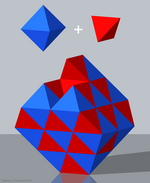Comprobación tetraédrica simple	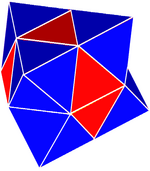Comprobación tetraédrica compleja
Politopos 4D
Tetroctaédrico	Octicosaédrico	Tetricosaédrico

En geometría , según la definición de Thorold Gosset , un politopo semirregular suele ser un politopo que es transitivo por vértices y tiene todas sus facetas siendo politopos regulares . EL Elte compiló una lista más larga en 1912 llamada Los politopos semirregulares de los hiperespacios que incluía una definición más amplia.

En el espacio tridimensional y en dimensiones inferiores, los términos politopo semirregular y politopo uniforme tienen significados idénticos, porque todos los polígonos uniformes deben ser regulares . Sin embargo, como no todos los poliedros uniformes son regulares , el número de politopos semirregulares en dimensiones superiores a tres es mucho menor que el número de politopos uniformes en el mismo número de dimensiones.

Los tres politopos semirregulares convexos de 4 celdas son el de 5 celdas rectificado , el de 24 celdas chato y el de 600 celdas rectificado . Los únicos politopos semirregulares en dimensiones superiores son los politopos k _{de 21} celdas , donde el de 5 celdas rectificado es el caso especial de k = 0. Todos ellos fueron enumerados por Gosset, pero no se publicó una prueba de la exhaustividad de esta lista hasta el trabajo de Makarov (1988) para cuatro dimensiones, y Blind & Blind (1991) para dimensiones superiores.

Los 4-politopos de Gosset (con sus nombres entre paréntesis)

Rectificado de 5 celdas (tetroctaédrico),

Rectificado de 600 celdas (Octicosaédrico),

Recortado de 24 celdas (tetricosaédrico),,o

Politopos E semirregulares en dimensiones superiores

5-demicube (5-ic semirregular), un 5-politopo ,↔

2 ₂₁ politopo (6-ic semirregular), un 6-politopo ,o

3 ₂₁ politopo (7-ic semirregular), un 7-politopo ,

4 ₂₁ politopo (8-ic semirregular), un 8-politopo ,

Los politopos semirregulares pueden extenderse a panales semirregulares . Los panales euclidianos semirregulares son el panal tetraédrico-octaédrico (3D), el panal cúbico alternado girado (3D) y el panal 5 ₂₁ (8D).

Panales de Gosset :

1. Panal tetraédrico-octaédrico o panal cúbico alternado (comprobación tetroctaédrica simple),↔(También politopo cuasirregular )
2. Panal cúbico alternado girado (complejo tetroctaédrico),

Panal electrónico semirregular:

• 5 ₂₁ panal (control 9-ic) (panal euclidiano 8D),

Gosset (1900) también admitió panales euclidianos como facetas de panales euclidianos de dimensiones superiores, dando las siguientes cifras adicionales:

1. Prisma de panal hipercúbico, denominado por Gosset como el semijaque ( n – 1)-ico (análogo a una sola fila o fila de un tablero de ajedrez)
2. Panal de abeja con losas hexagonales alternadas (semi-check tetroctahédrico),

También existen panales hiperbólicos uniformes compuestos únicamente de celdas regulares (Coxeter y Whitrow 1950), entre ellos:

• Panales hiperbólicos uniformes , panales 3D:
  1. Panal cúbico de orden alterno 5 ,↔(También politopo cuasirregular )
  2. Panal tetraédrico-octaédrico ,
  3. Panal de abeja tetraédrico- icosaédrico
• Panales uniformes paracompactos , panales tridimensionales, que incluyen teselas uniformes como celdas:
  1. Panal tetraédrico de orden 6 rectificado ,
  2. Revestimiento cuadrado rectificado en forma de panal ,
  3. Pedido rectificado - 4 baldosas cuadradas en forma de panal ,↔
  4. Orden alterno - 6 panales cúbicos↔(También cuasirregular)
  5. Panal de abeja con mosaico hexagonal alternado .↔
  6. Orden alterno - 4 mosaicos hexagonales en forma de panal↔
  7. Orden alterno-5 mosaico hexagonal en forma de panal ,↔
  8. Orden alterno - 6 mosaicos hexagonales en forma de panal↔
  9. Panal de abeja con mosaico cuadrado alternado ,↔(También cuasirregular)
  10. Panal de abeja con revestimiento cúbico-cuadrado .
  11. Orden-4 baldosas cuadradas en forma de panal ,=
  12. Panal de abeja con teselación tetraédrica-triangular .
• Panal paracompacto hiperbólico 9D:
  1. 6 ₂₁ panal (control 10-ic),

• Poliedro semirregular

• Ciego, G.; Ciego, R. (1991). "Los politopos semirregulares". Comentarios Mathematici Helvetici . 66 (1): 150-154. doi :10.1007/BF02566640. SEÑOR  1090169. S2CID  119695696.
• Coxeter, HSM (1973). Politopos regulares (3.ª ed.). Nueva York: Dover Publications. ISBN 0-486-61480-8.
• Coxeter, HSM ; Whitrow, GJ (1950). "Estructura mundial y panales no euclidianos". Actas de la Royal Society . 201 (1066): 417–437. Bibcode :1950RSPSA.201..417C. doi :10.1098/rspa.1950.0070. MR  0041576. S2CID  120322123.
• Elte, EL (1912). Los politopos semirregulares de los hiperespacios . Groningen: Universidad de Groningen. ISBN 1-4181-7968-X.
• Gosset, Thorold (1900). "Sobre las figuras regulares y semirregulares en el espacio de n dimensiones". Messenger of Mathematics . 29 : 43–48.
• Makarov, PV (1988). "Sobre la derivación de politopos semirregulares cuatridimensionales". Voprosy Diskret. Geom. Mat. Issled. Akad. Nauk. Mold . 103 : 139–150, 177. MR  0958024.