Resonador de anillo dividido
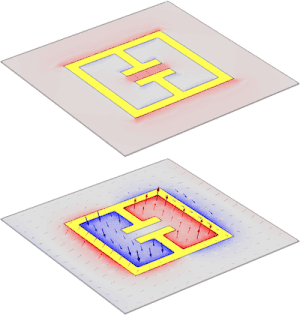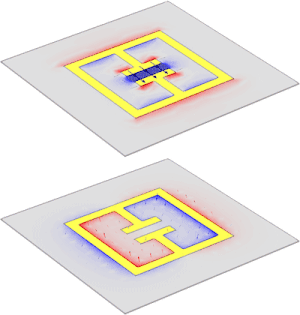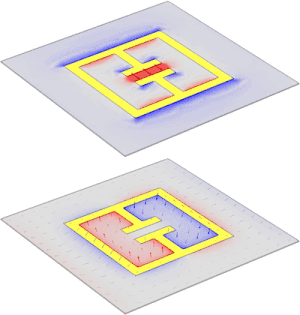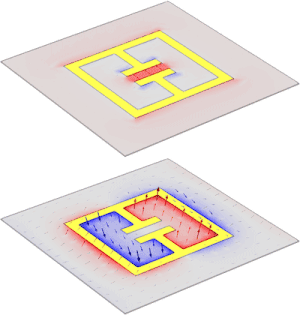
Un resonador
Un ejemplo de resonador de anillo dividido que consta de un cuadrado interior con una hendidura en un lado incrustado en un cuadrado exterior con una hendidura en el otro lado. Los resonadores de anillo dividido se encuentran en las superficies frontal y derecha de la rejilla cuadrada, y los cables verticales individuales se encuentran en las superficies posterior e izquierda. [1] [2]
Campo eléctrico (arriba) y campo magnético (abajo) de un SRR eléctrico bajo excitación eléctrica resonante. La respuesta magnética surge [ dudosa – discutir ] de la simetría de los bucles de corriente. [3]

Un resonador de anillo dividido ( SRR ) es una estructura producida artificialmente común en los metamateriales . Su propósito es producir la susceptibilidad magnética deseada (respuesta magnética) en varios tipos de metamateriales hasta 200 terahercios .

Fondo

Un resonador de anillo dividido. Observe que la corriente, indicada por la letra "i", circula en el sentido de las agujas del reloj.

Los resonadores de anillo dividido (SRR) consisten en un par de anillos metálicos concéntricos , grabados en un sustrato dieléctrico , con ranuras grabadas en lados opuestos. Los SRR pueden producir el efecto de ser eléctricamente más pequeños cuando responden a un campo electromagnético oscilante . Estos resonadores se han utilizado para la síntesis de medios de índice de refracción negativo y levógiro, donde el valor necesario de la permeabilidad efectiva negativa se debe a la presencia de los SRR. Cuando una matriz de SRR eléctricamente pequeños se excita por medio de un campo magnético variable en el tiempo , la estructura se comporta como un medio efectivo con permeabilidad efectiva negativa en una banda estrecha por encima de la resonancia SRR . Los SRR también se han acoplado a líneas de transmisión planas para la síntesis de líneas de transmisión de metamateriales. [4] [5] [6] [7] Estos medios crean el fuerte acoplamiento magnético necesario a un campo electromagnético aplicado que de otro modo no estaría disponible en materiales convencionales. Por ejemplo, un efecto como la permeabilidad negativa se produce con una matriz periódica de resonadores de anillo dividido. [8]

Un SRR de una sola celda tiene un par de bucles cerrados con divisiones en los extremos opuestos. Los bucles están hechos de un metal no magnético como el cobre y tienen un pequeño espacio entre ellos. Los bucles pueden ser concéntricos o cuadrados, y tener un espacio entre ellos según sea necesario. Un flujo magnético que penetra en los anillos de metal inducirá corrientes rotatorias en los anillos, que producen su propio flujo para mejorar u oponerse al campo incidente (dependiendo de las propiedades resonantes del SRR). Este patrón de campo es dipolar . Los pequeños espacios entre los anillos producen grandes valores de capacitancia , lo que reduce la frecuencia de resonancia . Por lo tanto, las dimensiones de la estructura son pequeñas en comparación con la longitud de onda resonante . Esto da como resultado bajas pérdidas radiativas y factores de calidad muy altos . [8] [9] [10]

El resonador de anillo dividido fue un diseño de microestructura que se presentó en el artículo de Pendry et al. en 1999 llamado "Magnetismo de conductores y fenómenos no lineales mejorados". [11] Propuso que el diseño del resonador de anillo dividido, construido a partir de material no magnético, podría mejorar la actividad magnética no observada en materiales naturales. En el diseño de microestructura simple, se muestra que en una matriz de cilindros conductores , con un campo externo aplicado paralelo a los cilindros, la permeabilidad efectiva se puede escribir de la siguiente manera. (Este modelo es muy limitado y la permeabilidad efectiva no puede ser menor que cero ni mayor que uno). [5] yo 0 Estilo de visualización H_{0}

micras mi F F = 1 − π a 2 a 2   ( 1 + i 2 σ ω a micras 0   ) − 1 {\displaystyle \mu _{eff}=1-{\frac {\pi r^{2}}{a^{2}}}\ \left(1+i{\frac {2\sigma }{\omega r\mu _{0}}}\ \right)^{-1}}

Donde es la resistencia de la superficie del cilindro por unidad de área, a es el espaciamiento de los cilindros, es la frecuencia angular, es la permeabilidad del espacio libre y r es el radio. Además, cuando se introducen espacios en un diseño de doble cilindro similar a la imagen de arriba, vemos que los espacios producen una capacitancia. Este diseño de microestructura de capacitor e inductor introduce una resonancia que amplifica el efecto magnético. La nueva forma de la permeabilidad efectiva se asemeja a una respuesta familiar [12] conocida en materiales plasmónicos. σ {\estilo de visualización \sigma} ω {\estilo de visualización \omega} micras 0 {\displaystyle \mu_{0}}

micras mi F F = 1 − π a 2 a 2   1 + 2 σ i ω a micras 0   − 3 d do 0 2 π 2 ω 2 a 3     {\displaystyle \mu _{eff}=1-{\frac {{\frac {\pi r^{2}}{a^{2}}}\ }{1+{\frac {2\sigma i}{\omega r\mu _{0}}}\ -{\frac {3dc_{0}^{2}}{\pi ^{2}\omega ^{2}r^{3}}}\ }}\ }

Donde d es el espaciamiento de las láminas conductoras concéntricas [ aclaración necesaria ] . El diseño final reemplaza los cilindros concéntricos dobles con un par de láminas planas concéntricas en forma de C, colocadas a cada lado de una celda unitaria. Las celdas unitarias están apiladas una sobre otra por una longitud l. El resultado final de la permeabilidad efectiva se puede ver a continuación.

micras mi F F = 1 − π a 2 a 2   1 + 2 yo σ 1 i ω a micras 0   − 3 yo do 0 2 π ω 2 a 3 yo norte ( 2 do d   )     {\displaystyle \mu _{eff}=1-{\frac {{\frac {\pi r^{2}}{a^{2}}}\ }{1+{\frac {2l\sigma _{1}i}{\omega r\mu _{0}}}\ -{\frac {3lc_{0}^{2}}{\pi \omega ^{2}r^{3}ln({\frac {2c}{d}}\ )}}\ }}\ }

donde c es el espesor de la lámina en forma de C y es la resistencia de la unidad de longitud de las láminas medida alrededor de la circunferencia. [5] σ {\estilo de visualización \sigma}

Características

El resonador de anillo dividido y el propio metamaterial son materiales compuestos. Cada SRR tiene una respuesta individual y personalizada al campo electromagnético. Sin embargo, la construcción periódica de muchas celdas SRR es tal que la onda electromagnética interactúa como si se tratara de materiales homogéneos . Esto es similar a cómo la luz interactúa realmente con los materiales cotidianos; los materiales como el vidrio o las lentes están hechos de átomos, se produce un efecto de promediado o macroscópico.

El SRR está diseñado para imitar la respuesta magnética de los átomos [ aclaración necesaria ] , solo que en una escala mucho mayor. Además, como parte de la estructura periódica compuesta, el SRR está diseñado para tener un acoplamiento magnético más fuerte que el que se encuentra en la naturaleza. La escala más grande permite un mayor control sobre la respuesta magnética, mientras que cada unidad es más pequeña que la onda electromagnética radiada .

Los SRR son mucho más activos [ aclaración necesaria ] que los materiales ferromagnéticos que se encuentran en la naturaleza. La respuesta magnética pronunciada en estos materiales livianos [ aclaración necesaria ] demuestra una ventaja sobre los materiales más pesados ​​que se encuentran en la naturaleza. Cada unidad puede diseñarse para que tenga su propia respuesta magnética. La respuesta puede mejorarse o reducirse según se desee. Además, el efecto general reduce los requisitos de energía. [8] [13]

Configuración de SRR

Existen diversos resonadores de anillos partidos y estructuras periódicas : anillos partidos de varilla, anillos partidos anidados, anillos partidos simples, anillos partidos deformados, anillos partidos en espiral y estructuras S extendidas. Las variaciones de los resonadores de anillos partidos han logrado diferentes resultados, incluidas estructuras más pequeñas y de mayor frecuencia. Las investigaciones que involucran algunos de estos tipos se analizan a lo largo del artículo. [14]

Hasta la fecha (diciembre de 2009) no se ha logrado la capacidad para obtener los resultados deseados en el espectro visible . Sin embargo, en 2005 se observó que, físicamente, un resonador de anillo dividido circular anidado debe tener un radio interno de 30 a 40 nanómetros para tener éxito en el rango medio del espectro visible. [14] Las técnicas de microfabricación y nanofabricación pueden utilizar escritura directa con haz de láser o litografía con haz de electrones según la resolución deseada. [14]

Varias configuraciones

Un conjunto de resonadores de anillo dividido está configurado como un material que produce un índice de refracción negativo . Se construyó con resonadores de anillo dividido de cobre y cables montados sobre láminas entrelazadas de una placa de circuito de fibra de vidrio. El conjunto total consta de 3 celdas unitarias de 20×20 con dimensiones generales de 10×100×100 mm. [1] [15]

Los resonadores de anillo dividido (SRR) son uno de los elementos más comunes utilizados para fabricar metamateriales . [16] Los resonadores de anillo dividido son materiales no magnéticos , que inicialmente se fabricaron a partir de material de placa de circuito para crear metamateriales. [17]

Mirando la imagen directamente a la derecha, se puede ver que al principio un SRR único parece un objeto con dos perímetros cuadrados, con cada perímetro con una pequeña sección eliminada. Esto da como resultado formas de "C" cuadradas en el material de la placa de circuito impreso de fibra de vidrio . [16] [17] En este tipo de configuración, en realidad son dos bandas concéntricas de material conductor no magnético . [16] Hay un espacio en cada banda colocada 180° una con respecto a la otra. [16] El espacio en cada banda le da la forma distintiva de "C", en lugar de una forma totalmente circular o cuadrada. [16] [17] Luego, se fabrican múltiples celdas de esta configuración de doble banda sobre el material de la placa de circuito mediante una técnica de grabado y se recubren con conjuntos de tiras de alambre de cobre. [17] Después del procesamiento, las placas se cortan y se ensamblan en una unidad entrelazada. [17] Se construye en una matriz periódica con una gran cantidad de SRR. [17]

Actualmente existen varias configuraciones diferentes que utilizan la nomenclatura SRR.

Manifestaciones

Se utilizó una matriz periódica de SRR para la primera demostración de un índice de refracción negativo . [17] Para esta demostración, se fabricaron SRR de forma cuadrada , con las configuraciones de alambre alineado, en una estructura de celda periódica y dispuesta. [17] Esta es la sustancia del metamaterial. [17] Luego se cortó un prisma metamaterial de este material. [17] El experimento del prisma demostró un índice de refracción negativo por primera vez en el año 2000; el artículo sobre la demostración se envió a la revista Science el 8 de enero de 2001, se aceptó el 22 de febrero de 2001 y se publicó el 6 de abril de 2001. [17]

Justo antes de este experimento con prismas, Pendry et al. pudieron demostrar que una matriz tridimensional de cables delgados que se entrecruzaban podía usarse para crear valores negativos de ε. En una demostración posterior, una matriz periódica de resonadores de anillo dividido de cobre podía producir un μ negativo efectivo. En 2000, Smith et al. fueron los primeros en combinar con éxito las dos matrices y producir un material denominado zurdo , que tiene valores negativos de ε y μ para una banda de frecuencias en el rango de GHz. [17]

Los SRR se utilizaron por primera vez para fabricar metamateriales zurdos para el rango de microondas , [17] y varios años después para el rango de terahercios . [18] Para 2007, muchos grupos habían logrado una demostración experimental de esta estructura en frecuencias de microondas. [19] Además, los SRR se han utilizado para la investigación en metamateriales acústicos. [20] Los SRR y cables dispuestos del primer metamaterial zurdo se fusionaron en capas alternas. [21] Este concepto y metodología se aplicaron luego a materiales (dieléctricos) con resonancias ópticas que producen permitividad efectiva negativa para ciertos intervalos de frecuencia, lo que resulta en " frecuencias de banda prohibida fotónicas ". [20] Otro análisis mostró que los materiales zurdos se fabrican a partir de constituyentes no homogéneos, lo que sin embargo da como resultado un material macroscópicamente homogéneo . [20] Los SRR se habían utilizado para enfocar una señal desde una fuente puntual, lo que aumenta la distancia de transmisión para ondas de campo cercano . [20] Además, otro análisis mostró SRR con un índice de refracción negativo capaz de una respuesta magnética de alta frecuencia , lo que creó un dispositivo magnético artificial compuesto de materiales no magnéticos (placa de circuito dieléctrico). [17] [20] [21]

Los fenómenos de resonancia que se producen en este sistema son esenciales para lograr los efectos deseados. [19]

Los SRR también exhiben una respuesta eléctrica resonante además de su respuesta magnética resonante. [21] La respuesta, cuando se combina con una matriz de cables idénticos, se promedia sobre toda la estructura compuesta, lo que da como resultado valores efectivos, incluido el índice de refracción. [22] La lógica original detrás de los SRR específicamente, y los metamateriales en general, era crear una estructura que imitara una estructura atómica ordenada solo que en una escala mucho mayor.

Varios tipos de SRR

En la investigación basada en metamateriales, y específicamente en índices de refracción negativos , existen diferentes tipos de resonadores de anillos partidos. De los ejemplos que se mencionan a continuación, la mayoría de ellos tienen un hueco en cada anillo. En otras palabras, con una estructura de doble anillo, cada anillo tiene un hueco. [23]

Existe la estructura de anillo dividido unidimensional con dos anillos cuadrados , uno dentro del otro. Un conjunto de dimensiones de " celda unitaria " citadas sería un cuadrado exterior de 2,62 mm y un cuadrado interior de 0,25 mm. Las estructuras unidimensionales como ésta son más fáciles de fabricar en comparación con la construcción de una estructura bidimensional rígida. [23]

La estructura de anillo simétrico es otro ejemplo clásico. Descrita por la nomenclatura, se trata de dos configuraciones rectangulares cuadradas de tipo D, exactamente del mismo tamaño, que se encuentran planas, una al lado de la otra, en la celda unitaria . Además, no son concéntricas . Un conjunto de dimensiones citadas son 2 mm en el lado más corto y 3,12 mm en el lado más largo. Los espacios en cada anillo se enfrentan entre sí, en la celda unitaria. [23]

La Estructura Omega , como describe la nomenclatura, tiene una estructura de anillo en forma de Ω. [24] Hay dos de estos, en posición vertical, uno al lado del otro, en lugar de estar planos, en la celda unitaria. En 2005, se los consideró un nuevo tipo de metamaterial. Un conjunto de dimensiones citadas son los parámetros anulares de R = 1,4 mm y r = 1 mm, y el borde recto es de 3,33 mm. [23]

Otro nuevo metamaterial que se descubrió en 2005 fue una estructura acoplada en forma de S. Hay dos estructuras verticales en forma de S, una al lado de la otra, en una celda unitaria. No hay un espacio como en la estructura de anillo; sin embargo, hay un espacio entre las partes superior e intermedia de la S y un espacio entre la parte intermedia y la parte inferior de la S. Además, todavía tiene las propiedades de tener una frecuencia de plasma eléctrico y una frecuencia de resonancia magnética. [23] [25]

Investigación

El 1 de mayo de 2000 se publicó una investigación sobre un experimento que implicaba colocar cables conductores simétricamente dentro de cada celda de un conjunto periódico de resonadores de anillo dividido . Esto logró de manera efectiva una permeabilidad y permitividad negativas para las ondas electromagnéticas en el régimen de microondas . El concepto se utilizó y todavía se utiliza para construir elementos interactuantes más pequeños que la radiación electromagnética aplicada. Además, el espaciamiento entre los resonadores es mucho menor que la longitud de onda de la radiación aplicada. [26]

Además, las divisiones en el anillo permiten que la unidad SRR logre resonancia en longitudes de onda mucho mayores que el diámetro del anillo. La unidad está diseñada para generar una gran capacitancia, reducir la frecuencia de resonancia y concentrar el campo eléctrico. La combinación de unidades crea un diseño como un medio periódico. Además, la estructura de unidades múltiples tiene un fuerte acoplamiento magnético con bajas pérdidas radiativas. [26] La investigación también ha cubierto variaciones en resonancias magnéticas para diferentes configuraciones de SRR. [27] [28] [29] La investigación ha continuado en radiaciones de terahercios con SRR [30] Otro trabajo relacionado diseñó configuraciones metamateriales con fractales [24] y estructuras no SRR. Estas pueden construirse con materiales como cruces metálicas periódicas o estructuras de anillo concéntrico cada vez más ancho conocidas como rollos suizos. [31] [32] [33] [34] Se ha analizado la permeabilidad solo para la longitud de onda roja a 780 nm y junto con otros trabajos relacionados. [35] [36] [37]

Véase también

Revistas académicas
Libros sobre metamateriales

Referencias

  1. ^ ab Smith, DR; Padilla, WJ; Vier, DC; Nemat-Nasser, SC; Schultz, S (2000). "Medio compuesto con permeabilidad y permitividad negativas simultáneas". Physical Review Letters . 84 (18): 4184–7. Bibcode :2000PhRvL..84.4184S. doi : 10.1103/PhysRevLett.84.4184 . PMID  10990641.
  2. ^ Shelby, RA; Smith, DR; Nemat-Nasser, SC; Schultz, S. (2001). "Transmisión de microondas a través de un metamaterial bidimensional, isotrópico y zurdo". Applied Physics Letters . 78 (4): 489. Bibcode :2001ApPhL..78..489S. doi :10.1063/1.1343489.
  3. ^ Degl'Innocenti, R. (2014). "Modulador de amplitud de terahercios de baja polarización basado en resonadores de anillo dividido y grafeno". ACS Nano . 8 (3): 2548–2554. doi :10.1021/nn406136c. PMID  24558983.
  4. ^ Naqui, Jordi; Durán-Sindreu, Miguel; Martín, Ferran (2011). "Nuevos sensores basados ​​en las propiedades de simetría de los resonadores de anillo partido (SRR)". Sensores . 11 (12): 7545–7553. Bibcode :2011Senso..11.7545N. doi : 10.3390/s110807545 . ISSN  1424-8220. PMC 3231717 . PMID  22164031. 
  5. ^ abc Pendry, JB; Holden, AJ; Robbins, DJ; Stewart, WJ (1999). "Magnetismo de conductores y fenómenos no lineales mejorados". IEEE Transactions on Microwave Theory and Techniques . 47 (11): 2075–2084. Bibcode :1999ITMTT..47.2075P. CiteSeerX 10.1.1.564.7060 . doi :10.1109/22.798002. ISSN  0018-9480. 
  6. ^ Smith, D.; Padilla, Willie; Vier, D.; Nemat-Nasser, S.; Schultz, S. (2000). "Medio compuesto con permeabilidad y permitividad negativas simultáneas". Physical Review Letters . 84 (18): 4184–4187. Bibcode :2000PhRvL..84.4184S. doi : 10.1103/PhysRevLett.84.4184 . ISSN  0031-9007. PMID  10990641.
  7. ^ Shelby, RA (2001). "Verificación experimental de un índice negativo de refracción". Science . 292 (5514): 77–79. Bibcode :2001Sci...292...77S. CiteSeerX 10.1.1.119.1617 . doi :10.1126/science.1058847. ISSN  0036-8075. PMID  11292865. S2CID  9321456. 
  8. ^ abc Gay-Balmaz, Philippe; Martin, Olivier JF (2002). "Resonancias electromagnéticas en resonadores de anillo dividido individuales y acoplados" (descarga gratuita en PDF) . Journal of Applied Physics . 92 (5): 2929. Bibcode :2002JAP....92.2929G. doi :10.1063/1.1497452.
  9. ^ Baena, JD; Bonache, J.; Martín, F.; Sillero, RM; Falcone, F.; Lopetegi, T.; Laso, MAG; García-García, J.; et al. (2005). "Modelos de circuito equivalente para resonadores de anillo dividido y resonadores de anillo dividido complementarios acoplados a líneas de transmisión planas" (PDF) . IEEE Transactions on Microwave Theory and Techniques . 53 (4): 1451–1461. Bibcode :2005ITMTT..53.1451B. doi :10.1109/TMTT.2005.845211. S2CID  18406919. Archivado desde el original (descarga gratuita en PDF) el 14 de octubre de 2009.
  10. ^ Marqués, R.; Martel, J.; Mesa, F.; Medina, F. (2002). "Simulación y transmisión de ondas electromagnéticas en medios zurdos en guías de ondas metálicas cargadas con resonador de anillo dividido de sublongitud de onda" (PDF) . Physical Review Letters . 89 (18): 183901. Bibcode :2002PhRvL..89r3901M. doi :10.1103/PhysRevLett.89.183901. hdl :11441/62810. PMID  12398601. S2CID  32685189. Archivado desde el original (descarga gratuita en PDF) el 14 de octubre de 2009.
  11. ^ John Brian Pendry; Anthony J. Holden; DJ Robbins; William James Stewart (1999). "Magnetismo de conductores y fenómenos no lineales mejorados". IEEE Transactions on Microwave Theory and Techniques . 47 (11): 2075–2084. Bibcode :1999ITMTT..47.2075P. doi :10.1109/22.798002.
  12. ^ Parsons, J.; Hendry, E.; Sambles, JR; Barnes, WL (23 de diciembre de 2009). "Resonancias de plasmón superficial localizadas e índice de refracción negativo en metamateriales electromagnéticos nanoestructurados". Physical Review B . 80 (24): 245117. Bibcode :2009PhRvB..80x5117P. doi :10.1103/PhysRevB.80.245117. ISSN  1098-0121.
  13. ^ Pendry, John B.; AJ Holden; DJ Robbins; WJ Stewart (3 de febrero de 1999). "Magnetismo de conductores y fenómenos no lineales mejorados" (PDF) . IEEE Trans. Microw. Theory Tech . 47 (11): 2075–2084. Bibcode :1999ITMTT..47.2075P. CiteSeerX 10.1.1.564.7060 . doi :10.1109/22.798002. Archivado desde el original (Descarga gratuita en PDF. Citado por 2136 artículos. PDF alternativo aquí Nov. 1999) el 2011-07-17 . Consultado el 2009-12-10 .  {{cite journal}}: Enlace externo en |format=( ayuda )
  14. ^ abc Moser, HO; et al. (8 de julio de 2005). Metamateriales electromagnéticos en todo el rango de THz: logros y perspectivas (Descarga gratuita en PDF, haga clic en el enlace) . p. 18. doi :10.1142/9789812701718_0003. ISBN 978-981-256-411-5. Consultado el 21 de octubre de 2009 . {{cite book}}: |journal=ignorado ( ayuda )
  15. ^ Shelby, RA; Smith DR; Shultz S.; Nemat-Nasser SC (2001). "Transmisión de microondas a través de un metamaterial bidimensional, isotrópico y zurdo" (PDF) . Applied Physics Letters . 78 (4): 489. Bibcode :2001ApPhL..78..489S. doi :10.1063/1.1343489.
  16. ^ abcde Lee, Yun-Shik (2008). Principios de la ciencia y la tecnología de los terahercios. Vol. Apuntes de clases de física. Nueva York: Springer-Verlag New York, LLC. págs. 1–3, 191. ISBN 978-0-387-09539-4.
  17. ^ abcdefghijklmn Shelby, RA; Smith, DR; Schultz, S (2001). "Verificación experimental de un índice negativo de refracción". Science . 292 (5514): 77–9. Bibcode :2001Sci...292...77S. CiteSeerX 10.1.1.119.1617 . doi :10.1126/science.1058847. PMID  11292865. S2CID  9321456. 
  18. ^ Yen, TJ; et al. (2004). "Respuesta magnética de terahercios de materiales artificiales". Science . 303 (5663): 1494–1496. Bibcode :2004Sci...303.1494Y. doi :10.1126/science.1094025. PMID  15001772. S2CID  14262927.
  19. ^ ab Kamil, Boratay Alici; Ekmel Özbay (22 de marzo de 2007). "Propiedades de radiación de un resonador de anillo dividido y un compuesto monopolar" (PDF) . Physica Status Solidi B . 244 (4): 1192–1196. Bibcode :2007PSSBR.244.1192A. doi :10.1002/pssb.200674505. hdl : 11693/49278 . S2CID  5348103 . Consultado el 17 de septiembre de 2009 .
  20. ^ abcde Movchan, AB; S. Guenneau (2004). "Resonadores de anillo dividido y modos localizados" (PDF) . Phys. Rev. B . 70 (12): 125116. Bibcode :2004PhRvB..70l5116M. doi :10.1103/PhysRevB.70.125116. Archivado desde el original (PDF) el 22 de febrero de 2016 . Consultado el 27 de agosto de 2009 .
  21. ^ abc Katsarakis, N.; T. Koschny; M. Kafesaki; EN Economou; CM Soukoulis (2004). "Acoplamiento eléctrico a la resonancia magnética de resonadores de anillo dividido" (PDF) . Appl. Phys. Lett . 84 (15): 2943–2945. arXiv : cond-mat/0407369 . Código Bibliográfico :2004ApPhL..84.2943K. doi :10.1063/1.1695439. S2CID  27509585 . Consultado el 15 de septiembre de 2009 .
  22. ^ Smith, DR; JJ Mock; AF Starr; D. Schurig (17 de marzo de 2005). "Un metamaterial de índice de gradiente". Phys. Rev. E . 71 (3): 036609. arXiv : physics/0407063 . Bibcode :2005PhRvE..71c6609S. doi :10.1103/PhysRevE.71.036609. PMID  15903607. S2CID  6121436.
  23. ^ abcde Wu, B.-I.; W. Wang; J. Pacheco; X. Chen; T. Grzegorczyk; JA Kong (2005). "Un estudio sobre el uso de metamateriales como sustrato de antena para mejorar la ganancia". Progreso en la investigación electromagnética . 51 : 295–328. doi : 10.2528/PIER04070701 .
  24. ^ ab Slyusar VI Metamateriales en soluciones de antena.// 7ma Conferencia Internacional sobre Teoría y Técnicas de Antenas ICATT'09, Lviv, Ucrania, 6 al 9 de octubre de 2009. - Pp. 19 - 24 [1]
  25. ^ J. Lezec, Henri; Jennifer A. Dionne; Harry A. Atwater (20 de abril de 2007). "Refracción negativa en frecuencias visibles" (PDF) . Science . 316 (5823): 430–2. Bibcode :2007Sci...316..430L. CiteSeerX 10.1.1.422.9475 . doi :10.1126/science.1139266. PMID  17379773. S2CID  35189301 . Consultado el 6 de octubre de 2009 . 
  26. ^ ab Smith DR, et al. (1 de mayo de 2000). "Medio compuesto con permeabilidad y permitividad negativas simultáneas". Physical Review Letters . 84 (18): 4184–7. Bibcode :2000PhRvL..84.4184S. doi : 10.1103/PhysRevLett.84.4184 . PMID  10990641.
  27. ^ Aydin, Koray; Irfan Bulu; Kaan Guven; Maria Kafesaki; Costas M Soukoulis; Ekmel Ozbay (8 de agosto de 2005). "Investigación de resonancias magnéticas para diferentes parámetros y diseños de SRR". New Journal of Physics . 7 (168): 168. Bibcode :2005NJPh....7..168A. doi : 10.1088/1367-2630/7/1/168 .
  28. ^ Prati, Prati (20 de febrero de 2004). "Cruce entre el tamaño de la celda y la longitud de onda de la radiación incidente en un metamaterial" (PDF) . Microwave and Optical Technology Letters . 40 (4): 269–272. doi :10.1002/mop.11349. S2CID  110004449. Archivado desde el original (PDF) el 23 de julio de 2011.
  29. ^ Wang, Bingnan; Jiangfeng Zhou; Thomas Koschny; Costas M. Soukoulis (24 de septiembre de 2008). "Propiedades no lineales de resonadores de anillo dividido" (PDF) . Optics Express . 16 (20): 16058–. arXiv : 0809.4045 . Bibcode :2008OExpr..1616058W. doi :10.1364/OE.16.016058. PMID  18825245. S2CID  9428274. Archivado desde el original (PDF) el 27 de mayo de 2010 . Consultado el 25 de octubre de 2009 .
  30. ^ Casse BD, et al. (2007). Towards 3D Electromagnetic Metamaterials in the THz Range (PDF) (Hacia metamateriales electromagnéticos tridimensionales en el rango de THz) . Novena conferencia internacional sobre instrumentación de radiación sincronotrón. Vol. 879. págs. 1462–1465. Código bibliográfico :2007AIPC..879.1462C. doi :10.1063/1.2436340. Archivado desde el original (PDF) el 12 de marzo de 2020. Consultado el 4 de diciembre de 2009 .
  31. ^ Dolling, G.; et al. (1 de diciembre de 2005). "Pares de hilos cortados y pares de placas como átomos magnéticos para metamateriales ópticos" (PDF) . Optics Letters . 30 (23): 3198–3200. arXiv : physics/0507045 . Bibcode :2005OptL...30.3198D. doi :10.1364/OL.30.003198. PMID  16342719. S2CID  7537807. Archivado desde el original (Descarga gratuita en PDF) el 2010-04-15 . Consultado el 2009-10-31 .
  32. ^ Paul, Oliver; et al. (28 de abril de 2008). "Metamaterial de índice negativo a granel en frecuencias de terahercios" (Descarga gratuita en PDF) . Optics Express . 16 (9): 6736–44. Bibcode :2008OExpr..16.6736P. doi : 10.1364/OE.16.006736 . PMID:  18545376. Consultado el 1 de noviembre de 2009 .
  33. ^ Pendry, J., "Los nuevos materiales electromagnéticos enfatizan lo negativo", Archivado el 17 de julio de 2011 en Wayback Machine , Physics World, 1–5, 2001
  34. ^ Wiltshire, MCK; Hajnal, J; Pendry, J; Edwards, D; Stevens, C (7 de abril de 2003). "Endoscopio metamaterial para transferencia de campo magnético: imágenes de campo cercano con cables magnéticos". Opt Express . 11 (7): 709–15. Bibcode :2003OExpr..11..709W. doi : 10.1364/OE.11.000709 . PMID  19461782.
  35. ^ Yuan, Hsiao-Kuan; et al. (5 de febrero de 2007). "Un material con permeabilidad negativa a la luz roja". Optics Express . 15 (3): 1076–83. arXiv : physics/0610118 . Código Bibliográfico :2007OExpr..15.1076Y. doi :10.1364/OE.15.001076. PMID  19532335. S2CID  5928393.
  36. ^ Cai, Wenshan; Chettiar, Reino Unido; Yuan, Hong Kong; De Silva, VC; Kildischev, AV; Drachev, vicepresidente; Shalaev, VM (2007). "Metamagnéticos con los colores del arcoíris". Óptica Express . 15 (6): 3333–3341. Código Bib : 2007OExpr..15.3333C. doi : 10.1364/OE.15.003333 . PMID  19532574 . Consultado el 21 de octubre de 2009 .
  37. ^ Enkrich, C.; et al. (2005). "Metamateriales magnéticos en frecuencias de telecomunicaciones y visibles". Phys. Rev. Lett . 95 (20): 203901. arXiv : cond-mat/0504774 . Bibcode :2005PhRvL..95t3901E. doi :10.1103/PhysRevLett.95.203901. PMID  16384056. S2CID  2975455.

Lectura adicional

  • Ates, Damla; Cakmak, Atilla Ozgur; Colak, Evrim; Zhao, Rongkuo; Soukoulis, CM; Ozbay, Ekmel (2010). "Mejora de la transmisión a través de aperturas profundas de sublongitud de onda utilizando resonadores de anillo dividido conectados" (Descarga gratuita en PDF) . Optics Express . 18 (4): 3952–66. Bibcode :2010OExpr..18.3952A. doi : 10.1364/OE.18.003952 . hdl :11693/13284. PMID  20389408.
  • Shepard, KW et al. Resonador de anillo dividido para el amplificador superconductor de iones pesados ​​Argonne. IEEE Transactions on Nuclear Science, VoL. NS-24, N0.3, JUNIO DE 1977.
Busque metamateriales en Wikcionario, el diccionario libre.
Busque resonador de anillo dividido en Wikcionario, el diccionario libre.
Wikimedia Commons tiene medios relacionados con Metamateriales.
Wikimedia Commons tiene medios relacionados con metamateriales .
  • Vídeo: Conferencia de John Pendry: La ciencia de la invisibilidad Abril 2009, SlowTV
  • Calculadora de resonador de anillo dividido: herramienta en línea para calcular el circuito equivalente LC y la frecuencia de resonancia de las topologías SRR y CSRR.
Obtenido de "https://es.wikipedia.org/w/index.php?title=Resonador_de_anillo_dividido&oldid=1242896666"