Engranaje

Un engranaje ^{[1] [2]} o rueda dentada ^{[3] [4] [5]} es una pieza de una máquina rotatoria que se utiliza normalmente para transmitir movimiento rotatorio y/o par mediante una serie de dientes que se acoplan con dientes compatibles de otro engranaje u otra pieza. Los dientes pueden ser salientes o cavidades integrales mecanizadas en la pieza, o clavijas separadas insertadas en ella. En este último caso, el engranaje suele denominarse rueda dentada . Un piñón puede ser una de esas clavijas ^{[6] [7] [8]} o el engranaje completo. ^{[9] [6] [8]} Dos o más engranajes engranados se denominan tren de engranajes .

El miembro más pequeño de un par de engranajes engranados se suele llamar piñón . Por lo general, los engranajes y los trenes de engranajes se pueden utilizar para intercambiar par por velocidad de rotación entre dos ejes u otras piezas giratorias y/o para cambiar el eje de rotación y/o para invertir el sentido de rotación. Un engranaje también se puede utilizar para transmitir fuerza lineal y/o movimiento lineal a una cremallera , una barra recta con una fila de dientes compatibles.

Los engranajes se encuentran entre las piezas mecánicas más comunes. Vienen en una gran variedad de formas y materiales, y se utilizan para muchas funciones y aplicaciones diferentes. Los diámetros pueden variar desde unos pocos μm en micromáquinas , ^[10] a unos pocos mm en relojes y juguetes a más de 10 metros en algunos equipos de minería. ^[11] Otros tipos de piezas que son algo similares en forma y función a los engranajes incluyen la rueda dentada , que está destinada a engranar con una cadena de eslabones en lugar de otro engranaje, y la polea de distribución , destinada a engranar una correa de distribución . La mayoría de los engranajes son redondos y tienen dientes iguales, diseñados para funcionar lo más suavemente posible; pero hay varias aplicaciones para engranajes no circulares , y el mecanismo de Ginebra tiene un funcionamiento extremadamente desigual, por diseño.

Los engranajes pueden considerarse como ejemplos de la "máquina" de palanca básica. ^[12] Cuando un engranaje pequeño impulsa a uno más grande, la ventaja mecánica de esta palanca ideal hace que el par T aumente pero la velocidad de rotación ω disminuya. El efecto opuesto se obtiene cuando un engranaje grande impulsa a uno pequeño. Los cambios son proporcionales a la relación de transmisión r , la relación de los números de dientes: es decir ,T2_​/T1_​⁠ = r = ⁠N º ₂/N° ₁⁠ , y ⁠ω2_​/ω ₁⁠ = ⁠1/a⁠ = ⁠N° ₁/N º ₂⁠ . Dependiendo de la geometría del par, el sentido de giro también puede invertirse (de horario a antihorario, o viceversa).

La mayoría de los vehículos tienen una transmisión o "caja de cambios" que contiene un conjunto de engranajes que pueden engranarse en múltiples configuraciones. La caja de cambios permite al operador variar el par que se aplica a las ruedas sin cambiar la velocidad del motor. Las cajas de cambios también se utilizan en muchas otras máquinas, como tornos y cintas transportadoras . En todos esos casos, términos como "primera marcha", "marcha alta" y "marcha atrás" se refieren a las relaciones de par generales de diferentes configuraciones de engrane, en lugar de a engranajes físicos específicos. Estos términos pueden aplicarse incluso cuando el vehículo no contiene realmente engranajes, como en una transmisión continuamente variable . ^[13]

Los primeros engranajes supervivientes datan del siglo IV a. C. en China ^[14] (época Zhan Guo – finales de la dinastía Zhou oriental ), y se han conservado en el Museo de Luoyang de la provincia de Henan, China .

En Europa, Aristóteles menciona engranajes alrededor del 330 a. C., como las ruedas motrices de los molinetes. Observó que la dirección de rotación se invierte cuando una rueda dentada impulsa a otra rueda dentada. Filón de Bizancio fue uno de los primeros en utilizar engranajes en dispositivos para elevar el agua. ^[15] Los engranajes aparecen en obras relacionadas con Herón de Alejandría , en el Egipto romano alrededor del año 50 d. C., ^[16] pero se remontan a la mecánica de la Biblioteca de Alejandría en el Egipto ptolemaico del siglo III a. C. , y fueron desarrollados en gran medida por el erudito griego Arquímedes (287-212 a. C.). ^[17] Los primeros engranajes supervivientes en Europa se encontraron en el mecanismo de Anticitera , un ejemplo de un dispositivo con engranajes muy temprano e intrincado, diseñado para calcular las posiciones astronómicas del sol, la luna y los planetas, y predecir eclipses . Su tiempo de construcción se estima ahora entre 150 y 100 a. C. ^{[18] [19] [20]}

El ingeniero chino Ma Jun ( c.  200-265 ) describió un carro que apuntaba hacia el sur . Un conjunto de engranajes diferenciales conectados a las ruedas y a un puntero en la parte superior del carro mantenían la dirección del carro inalterada mientras éste giraba. ^[21]

Otro ejemplo antiguo que sobrevive de mecanismo de engranajes es un complejo dispositivo calendárico que muestra la fase de la Luna, el día del mes y los lugares del Sol y la Luna en el Zodíaco, inventado en el imperio bizantino a principios del siglo VI. ^{[22] [23]}

Los relojes de agua mecánicos con engranajes se construyeron en China hacia el año 725. ^{[ cita requerida ]}

Alrededor de 1221, se construyó en Isfahán un astrolabio con engranajes que mostraba la posición de la luna en el zodíaco y su fase , y el número de días desde la luna nueva. ^[24]

El engranaje helicoidal fue inventado en el subcontinente indio , para su uso en desmotadoras de algodón , en algún momento entre los siglos XIII y XIV. ^[25]

Entre 1348 y 1364 , Giovanni Dondi dell'Orologio construyó un complejo reloj astronómico, llamado Astrarium . Tenía siete caras y 107 piezas móviles; mostraba las posiciones del sol, la luna y los cinco planetas conocidos entonces, así como los días festivos religiosos. ^[26] El reloj de la catedral de Salisbury , construido en 1386, es el reloj mecánico de engranajes más antiguo del mundo que todavía funciona.

El fabricante de relojes británico Joseph Williamson utilizó engranajes diferenciales en 1720. ^{[ cita requerida ]}

Sin embargo, los engranajes funcionales más antiguos fueron creados por la Naturaleza y se observan en las patas traseras de las ninfas del insecto cigarra Issus coleoptratus .

La palabra engranaje probablemente proviene del nórdico antiguo gørvi (plural gørvar ) 'vestimenta, engranaje', relacionado con gøra , gørva 'hacer, construir, construir; poner en orden, preparar', un verbo común en nórdico antiguo, "usado en una amplia gama de situaciones, desde escribir un libro hasta aderezar carne". En este contexto, el significado de 'rueda dentada en maquinaria' se atestiguó por primera vez en la década de 1520; el sentido mecánico específico de 'partes por las que un motor comunica movimiento' es de 1814; específicamente de un vehículo (bicicleta, automóvil, etc.) en 1888. ^[27]

Un cog es un diente de una rueda. Del inglés medio cogge, del nórdico antiguo (compárese con el noruego kugg ('cog'), el sueco kugg , kugge ('cog, diente')), del protogermánico * kuggō (compárese con el holandés kogge (' cojinete '), el alemán Kock ), del protoindoeuropeo * gugā ('joroba, bola') (compárese con el lituano gugà ('pomo, joroba, colina'), del PIE * gēw- ('doblar, arquear'). ^[28] Se usó por primera vez c. 1300 en el sentido de 'una rueda que tiene dientes o ruedas dentadas; finales del siglo XIV, 'diente en una rueda'; rueda dentada, principios del siglo XV. ^[29]

Los engranajes del mecanismo de Antikythera están hechos de bronce , y los primeros engranajes chinos que se conservan están hechos de hierro. Estos metales, así como el estaño , se han utilizado generalmente para relojes y mecanismos similares hasta el día de hoy.

Históricamente, los engranajes grandes, como los que se usaban en los molinos de harina , solían estar hechos de madera en lugar de metal. Eran ruedas dentadas, que se hacían insertando una serie de clavijas o piñones de madera alrededor del borde de una rueda. Los piñones solían estar hechos de madera de arce .

Los engranajes de madera han sido reemplazados gradualmente por otros de metal, como el hierro fundido al principio, luego el acero y el aluminio . El acero es el más comúnmente utilizado debido a su alta relación resistencia-peso y bajo costo. El aluminio no es tan fuerte como el acero para la misma geometría, pero es más liviano y más fácil de mecanizar. La pulvimetalurgia se puede utilizar con aleaciones que no se pueden fundir o mecanizar fácilmente.

Aun así, debido al costo u otras consideraciones, algunos de los primeros engranajes de metal tenían ruedas dentadas de madera, y cada diente formaba un tipo de unión de mortaja y espiga especializada "pasante" ^[30].

Más recientemente, los plásticos de ingeniería y los materiales compuestos han estado reemplazando a los metales en muchas aplicaciones, especialmente aquellas con velocidad y par moderados. No son tan fuertes como el acero, pero son más baratos, pueden fabricarse en masa mediante moldeo por inyección ^[31] y no necesitan lubricación. Los engranajes de plástico pueden incluso estar diseñados intencionalmente para ser la parte más débil de un mecanismo, de modo que en caso de atascamiento fallen primero y así evitar daños a partes más costosas. Estos engranajes de sacrificio pueden ser una alternativa más simple a otros dispositivos de protección contra sobrecargas, como embragues y motores con par o corriente limitados.

A pesar de las ventajas del metal y el plástico, la madera siguió utilizándose para engranajes de gran tamaño hasta hace un par de siglos, debido al coste, el peso, la tradición u otras consideraciones. En 1967, la Thompson Manufacturing Company de Lancaster, New Hampshire, todavía tenía un negocio muy activo en el suministro de decenas de miles de dientes de engranajes de arce al año, principalmente para su uso en fábricas de papel y molinos de harina , algunos de los cuales databan de hace más de 100 años. ^[32]

Las técnicas más comunes para la fabricación de engranajes son la fundición por inyección , en arena y a la cera perdida , la pulvimetalurgia , el troquelado y el tallado de engranajes .

A partir de 2014, se estima que el 80% de todos los engranajes producidos en todo el mundo se producen mediante moldeo de forma neta . Los engranajes moldeados generalmente se realizan mediante pulvimetalurgia, inyección de plástico o fundición a presión de metal. ^[33] Los engranajes producidos mediante pulvimetalurgia a menudo requieren un paso de sinterización después de retirarlos del molde. Los engranajes fundidos requieren tallado de engranajes u otro mecanizado para dar forma a los dientes con la precisión necesaria. La forma más común de tallado de engranajes es el tallado con fresa madre , pero se pueden utilizar en su lugar el moldeado de engranajes , el fresado y el brochado .

En los engranajes metálicos destinados a operaciones de servicio pesado, como las transmisiones de automóviles y camiones, los dientes reciben un tratamiento térmico para endurecerlos y hacerlos más resistentes al desgaste , dejando el núcleo blando pero resistente . Para los engranajes grandes que son propensos a deformarse, se utiliza una prensa de temple .

Los engranajes se pueden fabricar mediante impresión 3D ; sin embargo, esta alternativa normalmente se utiliza solo para prototipos o cantidades de producción muy limitadas, debido a su alto costo, baja precisión y resistencia relativamente baja de la pieza resultante.

Además de los trenes de engranajes, otros métodos alternativos de transmisión de torque entre partes no coaxiales incluyen cadenas de eslabones accionadas por ruedas dentadas, transmisiones por fricción , correas y poleas , acoplamientos hidráulicos y correas de distribución .

Una de las principales ventajas de los engranajes es que su cuerpo rígido y el enclavamiento perfecto de los dientes garantizan un seguimiento preciso de la rotación a lo largo del tren de engranajes, limitado únicamente por el juego y otros defectos mecánicos. Por este motivo, se los prefiere en aplicaciones de precisión, como los relojes. Los trenes de engranajes también pueden tener menos piezas separadas (solo dos) y tienen una pérdida de potencia mínima, un desgaste mínimo y una larga vida útil. Los engranajes también suelen ser la forma más eficiente y compacta de transmitir par entre dos ejes no paralelos.

Por otra parte, los engranajes son más caros de fabricar, pueden requerir lubricación periódica y pueden tener mayor masa e inercia rotacional que las poleas equivalentes. Más importante aún, la distancia entre los ejes de los engranajes acoplados es limitada y no se puede cambiar una vez que se fabrican. También hay aplicaciones en las que el deslizamiento por sobrecarga o transitorios (como ocurre con las correas, los sistemas hidráulicos y las ruedas de fricción) no solo es aceptable sino deseable.

Para fines de análisis básico, cada engranaje puede idealizarse como un cuerpo perfectamente rígido que, en funcionamiento normal, gira alrededor de un eje de rotación que está fijo en el espacio, sin deslizarse a lo largo de él. Así, cada punto del engranaje puede moverse solo a lo largo de un círculo que es perpendicular a su eje y centrado en él. En cualquier momento t , todos los puntos del engranaje estarán girando alrededor de ese eje con la misma velocidad angular ω ( t ), en el mismo sentido. La velocidad no necesita ser constante a lo largo del tiempo.

La superficie de acción del engranaje consta de todos los puntos de su superficie que, en funcionamiento normal, pueden entrar en contacto con el engranaje correspondiente con presión positiva . Todas las demás partes de la superficie son irrelevantes (excepto que no pueden ser cruzadas por ninguna parte del engranaje correspondiente). En un engranaje con N dientes, la superficie de trabajo tiene simetría rotacional N veces mayor sobre el eje, lo que significa que es congruente ^{[ se necesita desambiguación ]} consigo misma cuando el engranaje gira por ⁠1/norte⁠ de una vuelta.

Si el engranaje está destinado a transmitir o recibir par con un sentido definido solamente (en el sentido de las agujas del reloj o en sentido contrario con respecto a algún punto de referencia), la superficie de acción consta de N parches separados, las caras de los dientes ; que tienen la misma forma y están posicionadas de la misma manera en relación con el eje, espaciadas1/norte⁠ apartarse.

Si el par de torsión en cada engranaje puede tener ambos sentidos, la superficie de acción tendrá dos conjuntos de N caras de dientes; cada conjunto será efectivo solo mientras el par de torsión tenga un sentido específico, y los dos conjuntos se pueden analizar independientemente el uno del otro. Sin embargo, en este caso, el engranaje generalmente también tiene simetría de "inversión", de modo que los dos conjuntos de caras de dientes son congruentes después de que el engranaje se invierte. Esta disposición garantiza que los dos engranajes estén firmemente bloqueados juntos, en todo momento, sin juego .

Durante el funcionamiento, cada punto p de cada cara de diente entrará en contacto en algún momento con una cara de diente del engranaje correspondiente en algún punto q de una de sus caras de diente. En ese momento y en esos puntos, las dos caras deben tener la misma dirección perpendicular pero orientación opuesta. Pero como los dos engranajes giran alrededor de ejes diferentes, los puntos p y q se mueven a lo largo de círculos diferentes; por lo tanto, el contacto no puede durar más de un instante y p se deslizará entonces sobre la otra cara o dejará de estar en contacto con ella por completo.

Por otra parte, en cualquier momento dado hay al menos un par de puntos de contacto; normalmente más de uno, incluso una línea o superficie entera de contacto.

Los engranajes reales difieren de este modelo en muchos aspectos: no son perfectamente rígidos, su montaje no garantiza que el eje de rotación esté perfectamente fijado en el espacio, los dientes pueden tener formas y espaciados ligeramente diferentes, las caras de los dientes no son perfectamente lisas, etc. Sin embargo, estas desviaciones del modelo ideal se pueden ignorar para un análisis básico del funcionamiento de un conjunto de engranajes.

Un criterio para clasificar los engranajes es la posición relativa y la dirección de los ejes o la rotación de los engranajes que se van a engranar entre sí.

En la configuración más habitual, los ejes de rotación de los dos engranajes son paralelos y, por lo general, sus tamaños son tales que entran en contacto cerca de un punto entre los dos ejes. En esta configuración, los dos engranajes giran en sentidos opuestos.

En ocasiones, los ejes son paralelos pero un engranaje está encajado dentro del otro. En esta configuración, ambos engranajes giran en el mismo sentido.

Si los dos engranajes están cortados por un plano imaginario perpendicular a los ejes, cada sección de un engranaje interactuará únicamente con la sección correspondiente del otro engranaje. Por lo tanto, el tren de engranajes tridimensional puede entenderse como una pila de engranajes planos e infinitesimalmente delgados, es decir, esencialmente bidimensionales.

En una disposición cruzada , los ejes de rotación de los dos engranajes no son paralelos, sino que se cruzan en un ángulo arbitrario excepto cero o 180 grados.

Para un funcionamiento óptimo, cada rueda debe ser un engranaje cónico , cuya forma general es como una rebanada ( trunco ) de un cono cuyo vértice es el punto de encuentro de los dos ejes.

Los engranajes cónicos con igual número de dientes y ejes a 90 grados se denominan engranajes ingleteadores (EE. UU.) o ingleteadores (Reino Unido).

Independientemente del ángulo entre los ejes, el mayor de dos engranajes cónicos desiguales puede ser interno o externo, dependiendo del sentido de rotación relativo deseado. ^[34]

Si los dos engranajes están cortados por una esfera imaginaria cuyo centro es el punto donde se cruzan los dos ejes, cada sección permanecerá en la superficie de esa esfera mientras el engranaje gira, y la sección de un engranaje interactuará solo con la sección correspondiente del otro engranaje. De esta manera, un par de engranajes 3D engranados puede entenderse como una pila de engranajes anidados infinitamente delgados en forma de copa.

Se dice que los engranajes de un par coincidente están torcidos si sus ejes de rotación son líneas torcidas , es decir, ni paralelas ni se cruzan.

En este caso, la mejor forma para cada superficie de paso no es ni cilíndrica ni cónica, sino una porción de un hiperboloide de revolución. ^{[35] [36]} Estos engranajes se denominan hipoides para abreviar. Los engranajes hipoides se encuentran más comúnmente con ejes a 90 grados.

El contacto entre los dientes de los engranajes hipoides puede ser incluso más suave y gradual que con los dientes de los engranajes cónicos espirales, pero también tienen una acción deslizante a lo largo de los dientes engranados a medida que giran y, por lo tanto, generalmente requieren algunos de los tipos más viscosos de aceite para engranajes para evitar que se extruya de las caras de los dientes acoplados, el aceite normalmente se designa HP (para hipoide) seguido de un número que indica la viscosidad. Además, el piñón se puede diseñar con menos dientes que un piñón cónico espiral, con el resultado de que las relaciones de transmisión de 60:1 y más son factibles usando un solo juego de engranajes hipoides. ^[37] Este estilo de engranaje es más común en los trenes de transmisión de vehículos de motor, en conjunto con un diferencial . Mientras que un juego de engranajes de anillo y piñón regular (no hipoide) es adecuado para muchas aplicaciones, no es ideal para los trenes de transmisión de vehículos porque genera más ruido y vibración que un hipoide. Llevar los engranajes hipoides al mercado para aplicaciones de producción en masa fue una mejora de ingeniería de la década de 1920.

Se dice que un engranaje es externo si sus dientes están orientados generalmente lejos del eje de rotación, e interno en caso contrario. ^[34] En un par de ruedas iguales, solo una de ellas (la más grande) puede ser interna.

Una corona dentada o engranaje de contramarcha es aquella cuyos dientes sobresalen en ángulo recto respecto del plano. Una corona dentada también suele estar engranada con un mecanismo de escape, como los que se encuentran en los relojes mecánicos.

Los dientes de los engranajes suelen extenderse por todo el espesor del engranaje. Otro criterio para clasificar los engranajes es la dirección general de los dientes en esa dimensión. Este atributo se ve afectado por la posición relativa y la dirección de los ejes o la rotación de los engranajes que se van a engranar.

En un engranaje cilíndrico recto o de corte recto , las caras de los dientes son rectas a lo largo de la dirección paralela al eje de rotación. Cualquier cilindro imaginario con el mismo eje cortará los dientes a lo largo de líneas rectas paralelas.

Los dientes pueden ser internos o externos. Dos engranajes rectos engranan correctamente solo si se colocan en ejes paralelos. ^[38] Las cargas sobre los dientes no generan empuje axial. Los engranajes rectos son excelentes a velocidades moderadas, pero tienden a ser ruidosos a velocidades altas. ^[39]

En el caso de engranajes con ejes cruzados no paralelos, las caras de un engranaje de corte recto son partes de una superficie cónica general cuyas líneas generatrices pasan por el punto de encuentro de los dos ejes, lo que da como resultado un engranaje cónico . Dichos engranajes se utilizan generalmente solo a velocidades inferiores a 5 m/s (980 ft/min) o, para engranajes pequeños, 1000 rpm . ^[40]

En un engranaje fijo helicoidal o seco , las paredes de los dientes no son paralelas al eje de rotación, sino que están dispuestas en ángulo. Una superficie de paso imaginaria (cilindro, cono o hiperboloide, según las posiciones relativas del eje) intersecta cada cara del diente a lo largo de un arco de hélice . Los engranajes helicoidales pueden engranarse en orientaciones paralelas o paralelas. La primera se refiere a cuando los ejes son paralelos entre sí; esta es la orientación más común. En la segunda, los ejes no son paralelos y, en esta configuración, los engranajes a veces se conocen como "engranajes oblicuos".

Los dientes en ángulo se acoplan más gradualmente que los dientes de los engranajes rectos, lo que hace que giren de manera más suave y silenciosa. ^[41] Con engranajes helicoidales paralelos, cada par de dientes primero hace contacto en un solo punto en un lado de la rueda dentada; luego, una curva de contacto en movimiento crece gradualmente a través de la cara del diente hasta un máximo, luego retrocede hasta que los dientes rompen el contacto en un solo punto en el lado opuesto. En los engranajes rectos, los dientes se encuentran repentinamente en un contacto lineal en todo su ancho, lo que causa tensión y ruido. Los engranajes rectos producen un zumbido característico a altas velocidades. Por esta razón, los engranajes rectos se utilizan en aplicaciones de baja velocidad y en situaciones donde el control del ruido no es un problema, y ​​los engranajes helicoidales se utilizan en aplicaciones de alta velocidad, transmisión de gran potencia o donde la reducción del ruido es importante. ^[42] La velocidad se considera alta cuando la velocidad de la línea de paso supera los 25 m/s. ^[43]

Una desventaja de los engranajes helicoidales es el empuje resultante a lo largo del eje del engranaje, que debe absorberse mediante cojinetes de empuje adecuados . Sin embargo, este problema se puede evitar utilizando un engranaje de espiga o un engranaje helicoidal doble , que no tiene empuje axial y también proporciona autoalineación de los engranajes. Esto da como resultado un empuje axial menor que un engranaje recto comparable.

Una segunda desventaja de los engranajes helicoidales es también un mayor grado de fricción deslizante entre los dientes engranados, que a menudo se soluciona con aditivos en el lubricante.

Para una configuración "cruzada" o "sesgada", los engranajes deben tener el mismo ángulo de presión y paso normal; sin embargo, el ángulo de hélice y la orientación pueden ser diferentes. La relación entre los dos ejes está definida en realidad por el ángulo de hélice de los dos ejes y la orientación, como se define: ^[44]

${\displaystyle E=\beta _ {1}+\beta _ {2}}$para engranajes de la misma lateralidad,

${\displaystyle E=\beta _ {1}-\beta _ {2}}$para engranajes de sentido opuesto,

donde es el ángulo de hélice del engranaje. La configuración cruzada es menos sólida mecánicamente porque solo hay un contacto puntual entre los engranajes, mientras que en la configuración paralela hay un contacto lineal. ^[44]${\estilo de visualización \beta}$

Muy comúnmente, los engranajes helicoidales se utilizan con el ángulo de hélice de uno que tiene el negativo del ángulo de hélice del otro; a un par de estos también se lo puede denominar como que tiene una hélice dextrógira y una hélice levógira de ángulos iguales. Los dos ángulos iguales pero opuestos suman cero: el ángulo entre los ejes es cero, es decir, los ejes son paralelos . Cuando la suma o la diferencia (como se describe en las ecuaciones anteriores) no es cero, los ejes están cruzados . Para los ejes cruzados en ángulos rectos, los ángulos de hélice son del mismo tipo porque deben sumar 90 grados. (Este es el caso de los engranajes en la ilustración anterior: engranan correctamente en la configuración cruzada: para la configuración paralela, uno de los ángulos de hélice debe invertirse. Los engranajes ilustrados no pueden engranar con los ejes paralelos).

• Animación 3D de engranajes helicoidales (ejes paralelos)
• Animación 3D de engranajes helicoidales (eje cruzado)

Los engranajes helicoidales dobles superan el problema del empuje axial que presentan los engranajes helicoidales simples mediante el uso de un doble juego de dientes, inclinados en direcciones opuestas. Un engranaje helicoidal doble puede considerarse como dos engranajes helicoidales especulares montados muy juntos sobre un eje común. Esta disposición anula el empuje axial neto, ya que cada mitad del engranaje empuja en la dirección opuesta, lo que da como resultado una fuerza axial neta de cero. Esta disposición también puede eliminar la necesidad de cojinetes de empuje. Sin embargo, los engranajes helicoidales dobles son más difíciles de fabricar debido a su forma más complicada.

Los engranajes en espiga son un tipo especial de engranajes helicoidales. No tienen una ranura en el medio como otros engranajes helicoidales dobles; los dos engranajes helicoidales en espejo están unidos de modo que sus dientes forman una V. Esto también se puede aplicar a los engranajes cónicos , como en la transmisión final del Citroën Tipo A. Otro tipo de engranaje helicoidal doble es el engranaje Wüst .

Para ambas direcciones de rotación posibles, existen dos posibles disposiciones para los engranajes helicoidales o caras de engranajes orientados en sentido opuesto. Una disposición se denomina estable y la otra inestable. En una disposición estable, las caras de los engranajes helicoidales están orientadas de modo que cada fuerza axial se dirige hacia el centro del engranaje. En una disposición inestable, ambas fuerzas axiales se dirigen en dirección contraria al centro del engranaje. En cualquiera de las disposiciones, la fuerza axial total (o neta ) sobre cada engranaje es cero cuando los engranajes están alineados correctamente. Si los engranajes se desalinean en la dirección axial, la disposición inestable genera una fuerza neta que puede provocar el desmontaje del tren de engranajes, mientras que la disposición estable genera una fuerza correctiva neta. Si se invierte la dirección de rotación, también se invierte la dirección de los empujes axiales, por lo que una configuración estable se vuelve inestable y viceversa.

Los engranajes helicoidales dobles estables se pueden intercambiar directamente con engranajes rectos sin necesidad de cojinetes diferentes.

Los gusanos se parecen a tornillos . Un gusano está engranado con una rueda helicoidal , que parece similar a un engranaje recto .

Los conjuntos de engranajes sinfín son una forma sencilla y compacta de lograr una relación de transmisión de alta torsión y baja velocidad. Por ejemplo, los engranajes helicoidales normalmente están limitados a relaciones de transmisión de menos de 10:1, mientras que los conjuntos de engranajes sinfín varían de 10:1 a 500:1. ^[45] Una desventaja es el potencial de una acción de deslizamiento considerable, lo que conduce a una baja eficiencia. ^[46]

Un engranaje helicoidal es una especie de engranaje helicoidal, pero su ángulo de hélice suele ser algo grande (cerca de 90 grados) y su cuerpo suele ser bastante largo en la dirección axial. Estos atributos le dan cualidades similares a las de un tornillo. La distinción entre un tornillo sin fin y un engranaje helicoidal es que al menos un diente persiste durante una rotación completa alrededor de la hélice. Si esto ocurre, es un "sinfín"; si no, es un "engranaje helicoidal". Un sinfín puede tener tan solo un diente. Si ese diente persiste durante varias vueltas alrededor de la hélice, el sinfín parece, superficialmente, tener más de un diente, pero lo que uno ve de hecho es el mismo diente reapareciendo a intervalos a lo largo de la longitud del sinfín. Se aplica la nomenclatura habitual de los tornillos: un sinfín con un solo diente se llama de rosca simple o de entrada simple ; un sinfín con más de un diente se llama de rosca múltiple o de entrada múltiple . El ángulo de hélice de un sinfín no suele especificarse. En su lugar, se da el ángulo de avance, que es igual a 90 grados menos el ángulo de la hélice.

En un conjunto de tornillo sin fin y engranaje, el tornillo sin fin siempre puede accionar el engranaje. Sin embargo, si el engranaje intenta accionar el tornillo sin fin, puede que lo consiga o no . En particular, si el ángulo de avance es pequeño, los dientes del engranaje pueden simplemente bloquearse contra los dientes del tornillo sin fin, porque el componente de fuerza circunferencial al tornillo sin fin no es suficiente para superar la fricción. Sin embargo, en las cajas de música tradicionales , el engranaje acciona el tornillo sin fin, que tiene un ángulo de hélice grande. Esta malla acciona las paletas del limitador de velocidad que están montadas en el eje del tornillo sin fin.

Los conjuntos de tornillo sin fin y engranaje que se bloquean se denominan autoblocantes , lo que puede resultar ventajoso, por ejemplo, cuando se desea fijar la posición de un mecanismo girando el tornillo sin fin y que el mecanismo mantenga esa posición. Un ejemplo es el clavijero que se encuentra en algunos tipos de instrumentos de cuerda .

Si el engranaje de un conjunto de tornillo sin fin y engranaje es un engranaje helicoidal ordinario, solo se logra un único punto de contacto. ^{[37] [47]} Si se desea una transmisión de potencia media a alta, se modifica la forma de los dientes del engranaje para lograr un contacto más íntimo haciendo que ambos engranajes se envuelvan parcialmente entre sí. Esto se hace haciendo que ambos sean cóncavos y uniéndolos en un punto de silla de montar ; esto se llama accionamiento cónico ^[48] o "doble envolvente".

Los engranajes helicoidales pueden ser de giro a derechas o a izquierdas, siguiendo la práctica establecida desde hace mucho tiempo para las roscas de tornillo. ^[34]

Otro criterio para clasificar los engranajes es el perfil del diente , la forma de la sección transversal de la cara de un diente mediante un corte imaginario perpendicular a la superficie de paso, como el plano transversal, normal o axial.

El perfil de los dientes es crucial para la suavidad y uniformidad del movimiento de los engranajes coincidentes, así como para la fricción y el desgaste.

Los dientes de los engranajes antiguos o artesanales que se cortaban a mano a partir de material laminado, como los del mecanismo de Antikhytera, generalmente tenían perfiles simples, como triángulos. ^[49] Los dientes de los engranajes más grandes, como los utilizados en los molinos de viento, generalmente eran clavijas con formas simples como cilindros, paralelepípedos o prismas triangulares insertados en una rueda lisa de madera o metal; o eran agujeros con formas igualmente simples cortados en dicha rueda.

Debido a su perfil subóptimo, la relación de transmisión efectiva de estos engranajes artesanales no era constante, sino que fluctuaba en cada ciclo de diente, lo que generaba vibraciones, ruido y desgaste acelerado.

Un engranaje de jaula , también llamado engranaje de linterna o piñón de linterna, es uno de esos engranajes artesanales que tienen varillas cilíndricas en lugar de dientes, paralelas al eje y dispuestas en un círculo alrededor de él, como las barras de una jaula de pájaros o linterna redonda. El conjunto se mantiene unido mediante discos en cada extremo, en los que se colocan las varillas dentadas y el eje. Los engranajes de jaula son más eficientes que los piñones sólidos, ^{[ cita requerida ]} y la suciedad puede caer a través de las varillas en lugar de quedar atrapada y aumentar el desgaste. Se pueden construir con herramientas muy simples, ya que los dientes no se forman cortando o fresando, sino perforando agujeros e insertando varillas.

En ocasiones, los engranajes de jaula se utilizan en relojes y siempre deben ser accionados por una rueda dentada, no como elemento impulsor. Los fabricantes de relojes conservadores no los favorecieron inicialmente, pero se hicieron populares en los relojes de torreta, donde las condiciones de trabajo sucias eran más habituales. Los mecanismos de relojería domésticos estadounidenses los utilizaban a menudo. ^{[ cita requerida ]}

En la mayoría de los engranajes modernos, el perfil de los dientes no suele ser recto ni circular, sino de una forma especial diseñada para lograr una relación de velocidad angular constante.

Existe una variedad infinita de perfiles de dientes que permiten lograr este objetivo. De hecho, dada una forma de diente bastante arbitraria, es posible desarrollar un perfil de diente para el engranaje de acoplamiento que lo logre.

Sin embargo, dos perfiles de dientes de velocidad constante son los más utilizados en la actualidad para engranajes con ejes paralelos o cruzados, basados ​​en las curvas cicloides e involutas .

Los engranajes cicloidales fueron más comunes hasta finales del siglo XIX. Desde entonces, la involuta la ha reemplazado en gran medida, particularmente en aplicaciones de transmisión. La cicloide es en algunos aspectos la forma más interesante y flexible; sin embargo, la involuta tiene dos ventajas: es más fácil de fabricar y permite que el espaciado entre centros de los engranajes varíe en un rango determinado sin arruinar la constancia de la relación de velocidad. Los engranajes cicloidales solo funcionan correctamente si el espaciado entre centros es exactamente el correcto. Los engranajes cicloidales todavía se utilizan comúnmente en los relojes mecánicos.

Para ejes no paralelos con cortes de dientes no rectos, el mejor perfil de diente es una de varias formas de engranaje cónico espiral . Estas incluyen los tipos Gleason (arco circular con profundidad de diente no constante), los tipos Oerlikon y Curvex (arco circular con profundidad de diente constante), Klingelnberg Cyclo-Palloid (Epicicloide con profundidad de diente constante) o Klingelnberg Palloid. ^[40]

Las caras de los dientes en estos tipos de engranajes no son cilindros o conos evolventes, sino parches de superficies octoidales. ^{[50] La fabricación de dichas caras de dientes puede requerir una} fresadora de 5 ejes .

Los engranajes cónicos espirales tienen las mismas ventajas y desventajas en relación con sus primos de corte recto que los engranajes helicoidales en relación con los engranajes rectos, como menor ruido y vibración. ^[40] Los engranajes cónicos calculados de manera simplificada sobre la base de un engranaje cilíndrico equivalente en sección normal con una forma de diente evolvente muestran una forma de diente desviada con una resistencia de diente reducida en un 10-28% sin desplazamiento y en un 45% con desplazamiento. ^[51]

Una cremallera es una barra o varilla dentada que puede considerarse como un engranaje sectorial con un radio de curvatura infinitamente grande . El par se puede convertir en fuerza lineal al engranar una cremallera con un engranaje redondo llamado piñón : el piñón gira, mientras que la cremallera se mueve en línea recta. Este mecanismo se utiliza en la dirección de los automóviles para convertir la rotación del volante en el movimiento de izquierda a derecha de la (s) barra (s) de dirección que están unidas a las ruedas delanteras.

Las cremalleras también forman parte de la teoría de la geometría de los engranajes, donde, por ejemplo, la forma de los dientes de un conjunto intercambiable de engranajes puede especificarse para la cremallera (radio infinito), y las formas de los dientes para engranajes de radios reales particulares se derivan de eso. El tipo de engranaje de cremallera y piñón también se utiliza en un ferrocarril de cremallera .

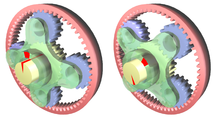
En los engranajes epicicloidales, uno o más de los ejes del engranaje se mueven. Algunos ejemplos son los engranajes planetarios (ver a continuación), la transmisión cicloidal , las transmisiones automáticas y los diferenciales mecánicos .

El engranaje solar y planetario es un método para convertir el movimiento alternativo en movimiento rotatorio que se utilizaba en las máquinas de vapor . James Watt lo utilizó en sus primeras máquinas de vapor para evitar la patente de la manivela , pero también proporcionó la ventaja de aumentar la velocidad del volante de inercia para que Watt pudiera utilizar un volante de inercia más ligero.

En la ilustración, el sol es amarillo, el planeta rojo, el brazo alternativo es azul, el volante es verde y el eje de transmisión es gris.

Los engranajes no circulares están diseñados para fines especiales. Mientras que un engranaje regular está optimizado para transmitir par a otro miembro acoplado con mínimo ruido y desgaste y máxima eficiencia , el objetivo principal de un engranaje no circular puede ser variaciones de relación , oscilaciones de desplazamiento de ejes y más. Las aplicaciones comunes incluyen máquinas textiles, potenciómetros y transmisiones continuamente variables .

La mayoría de los engranajes son cuerpos rígidos ideales que transmiten par y movimiento a través del principio de palanca y las fuerzas de contacto entre los dientes. Es decir, el par aplicado a un engranaje hace que gire como un cuerpo rígido, de modo que sus dientes empujan contra los del engranaje correspondiente, que a su vez gira como un cuerpo rígido y transmite el par a su eje. Sin embargo, algunos engranajes especializados escapan a este patrón.

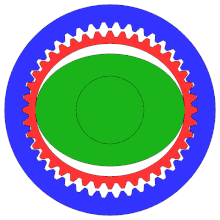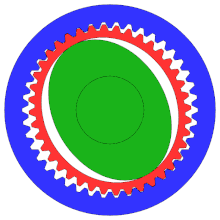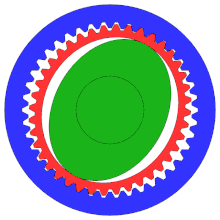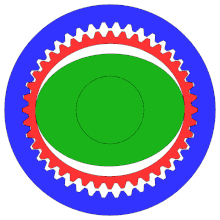
Un engranaje armónico o engranaje de onda de tensión es un mecanismo de engranaje especializado que se utiliza a menudo en el control de movimiento industrial , la robótica y la industria aeroespacial por sus ventajas sobre los sistemas de engranajes tradicionales, incluida la falta de juego, la compacidad y las altas relaciones de transmisión.

Aunque el diagrama no demuestra la configuración correcta, se trata de un "engranaje de distribución", convencionalmente con muchos más dientes que un engranaje tradicional para garantizar un mayor grado de precisión.

En un par de engranajes magnéticos no hay contacto entre los dos miembros; el par se transmite a través de campos magnéticos. Los dientes de cada engranaje son imanes constantes con alternancia periódica de polos magnéticos opuestos en superficies de acoplamiento. Los componentes del engranaje están montados con una capacidad de juego similar a otros engranajes mecánicos. Aunque no pueden ejercer tanta fuerza como un engranaje tradicional debido a los límites de la intensidad del campo magnético, estos engranajes funcionan sin tocarse y, por lo tanto, son inmunes al desgaste, tienen muy poco ruido, pérdidas mínimas de potencia por fricción y pueden deslizarse sin sufrir daños, lo que los hace muy confiables. ^[52] Se pueden utilizar en configuraciones que no son posibles para engranajes que deben estar en contacto físico y pueden funcionar con una barrera no metálica que separa completamente la fuerza motriz de la carga. El acoplamiento magnético puede transmitir fuerza a un recinto herméticamente sellado sin utilizar un sello de eje radial , que puede tener fugas.

Frecuencia de rotación , n

Medido en rotación a lo largo del tiempo, como revoluciones por minuto (RPM o rpm).

Frecuencia angular , ω

Medido en radianes por segundo . 1  RPM = 2 π  rad/minuto =π/30rad  /segundo.

Número de dientes, N

Cuántos dientes tiene un engranaje, un número entero . En el caso de los sinfines, es el número de entradas de rosca que tiene el sinfín.

Engranaje, rueda

El más grande de dos engranajes en interacción o un engranaje solo.

Piñón

El más pequeño de dos engranajes en interacción.

Ruta de contacto

Trayectoria seguida por el punto de contacto entre dos dientes de engranaje que engranan.

Línea de acción, línea de presión.

Línea a lo largo de la cual se dirige la fuerza entre dos dientes de engranaje engranados. Tiene la misma dirección que el vector de fuerza. En general, la línea de acción cambia de un momento a otro durante el período de engrane de un par de dientes. Sin embargo, para los engranajes evolventes , la fuerza entre dientes siempre se dirige a lo largo de la misma línea, es decir, la línea de acción es constante. Esto implica que, para los engranajes evolventes, la trayectoria de contacto también es una línea recta, coincidente con la línea de acción, como de hecho es el caso.

Eje

Eje de revolución del engranaje; línea central del eje.

Punto de lanzamiento

Punto donde la línea de acción cruza una línea que une los dos ejes del engranaje.

Círculo primitivo, línea primitiva

Círculo centrado y perpendicular al eje, que pasa por el punto de paso. Posición diametral predefinida en el engranaje donde se definen el espesor del diente circular, el ángulo de presión y los ángulos de hélice.

Diámetro de paso, d

Una posición diametral predefinida en el engranaje donde se definen el espesor circular del diente, el ángulo de presión y los ángulos de hélice. El diámetro de paso estándar es una dimensión de diseño y no se puede medir, sino que es una ubicación donde se realizan otras mediciones. Su valor se basa en el número de dientes ( N ), el módulo normal ( m _n ; o paso diametral normal, P _d ) y el ángulo de hélice ( ):${\estilo de visualización \psi}$

${\displaystyle d={\frac {Nm_{n}}{\cos \psi }}}$en unidades métricas o en unidades imperiales. ^[53]${\displaystyle d={\frac {N}{P_{d}\cos \psi }}}$

Módulo o módulo, m

Dado que no resulta práctico calcular el paso circular con números irracionales , los ingenieros mecánicos suelen utilizar un factor de escala que lo reemplaza por un valor regular. Esto se conoce como módulo de la rueda y se define simplemente como:

${\displaystyle m={\frac {p}{\pi }}}$

donde m es el módulo y p el paso circular. Las unidades del módulo son habitualmente milímetros ; a veces se utiliza un módulo inglés con las unidades de pulgadas . Cuando el paso diametral, DP, está en unidades inglesas,

${\displaystyle m={\frac {25.4}{DP}}}$en unidades métricas convencionales.

La distancia entre los dos ejes se convierte en:

${\displaystyle a={\frac {m}{2}}(z_{1}+z_{2})}$

donde a es la distancia entre ejes, z ₁ y z ₂ son el número de engranajes (piñones) para cada una de las dos ruedas (engranajes). Estos números (o al menos uno de ellos) se eligen a menudo entre primos para crear un contacto uniforme entre cada engranaje de ambas ruedas y, de ese modo, evitar desgaste y daños innecesarios. Se logra un desgaste uniforme de los engranajes al asegurar que el número de dientes de los dos engranajes que engranan entre sí sea relativamente primo entre sí; esto ocurre cuando el máximo común divisor (MCD) de cada número de dientes de engranaje es igual a 1, p. ej., MCD(16,25)=1; si se desea una relación de engranajes de 1:1, se puede insertar un engranaje relativamente primo entre los dos engranajes; esto mantiene la relación 1:1 pero invierte la dirección del engranaje; también se podría insertar un segundo engranaje relativamente primo para restaurar la dirección de rotación original mientras se mantiene un desgaste uniforme con los 4 engranajes en este caso. Los ingenieros mecánicos, al menos en Europa continental, suelen utilizar el módulo en lugar del paso circular. El módulo, al igual que el paso circular, se puede utilizar para todo tipo de engranajes, no solo para engranajes rectos basados ​​en Evolutionnt . ^[54]

Diámetros de paso de operación

Diámetros determinados a partir del número de dientes y la distancia entre centros a los que operan los engranajes. ^[34] Ejemplo de piñón:

${\displaystyle d_{w}={\frac {2a}{u+1}}={\frac {2a}{{\frac {z_{2}}{z_{1}}}+1}}.}$

Superficie del terreno de juego

En los engranajes cilíndricos, cilindro formado al proyectar un círculo primitivo en dirección axial. En términos más generales, superficie formada por la suma de todos los círculos primitivos a medida que uno se mueve a lo largo del eje. En los engranajes cónicos, es un cono.

Angulo de accion

Ángulo con vértice en el centro del engranaje, una pata en el punto donde los dientes acoplados hacen contacto por primera vez, la otra pata en el punto donde se desenganchan.

Arco de acción

Segmento de un círculo primitivo subtendido por el ángulo de acción.

Ángulo de presión , θ

Complemento del ángulo entre la dirección en la que los dientes ejercen fuerza entre sí y la línea que une los centros de los dos engranajes. En el caso de los engranajes evolventes, los dientes siempre ejercen fuerza a lo largo de la línea de acción, que, en el caso de los engranajes evolventes, es una línea recta; por lo tanto, en el caso de los engranajes evolventes, el ángulo de presión es constante.

Diámetro exterior, D _o

Diámetro del engranaje, medido desde la parte superior de los dientes.

Diámetro de la raíz

Diámetro del engranaje, medido en la base del diente.

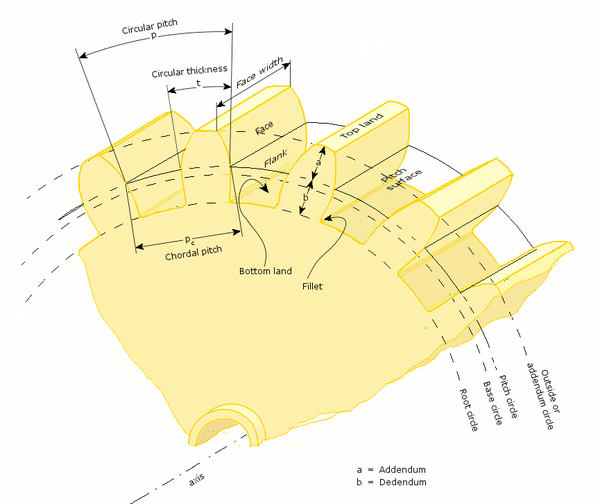
Adenda, una

Distancia radial desde la superficie de paso hasta el punto más externo del diente.${\displaystyle a={\frac {1}{2}}(D_{o}-D)}$

Dedendum, b

Distancia radial desde la profundidad del canal del diente hasta la superficie de paso.${\displaystyle b={\frac {1}{2}}(D-{\text{diámetro de la raíz}})}$

Profundidad total, h _t

La distancia desde la parte superior del diente hasta la raíz; es igual a addendum más dedendum o a profundidad de trabajo más espacio libre.

Autorización

Distancia entre el círculo raíz de un engranaje y el círculo superior de su pareja.

Profundidad de trabajo

Profundidad de engrane de dos engranajes, es decir, la suma de sus adendas de funcionamiento.

Paso circular, p

Distancia desde una cara de un diente a la cara correspondiente de un diente adyacente en el mismo engranaje, medida a lo largo del círculo primitivo.

Paso diametral, DP

${\displaystyle DP={\frac {N}{d}}={\frac {\pi }{p}}}$

Relación entre el número de dientes y el diámetro de paso. Puede medirse en dientes por pulgada o dientes por centímetro, pero convencionalmente tiene unidades de por pulgada de diámetro. Donde el módulo, m , está en unidades métricas .

${\displaystyle DP={\frac {25.4}{m}}}$en unidades imperiales

Circulo base

En los engranajes evolventes, el perfil de los dientes se genera por la evolvente del círculo base. El radio del círculo base es algo menor que el del círculo primitivo.

Tono base, tono normal, p _b

En engranajes evolventes, distancia desde una cara de un diente a la cara correspondiente de un diente adyacente en el mismo engranaje, medida a lo largo del círculo base.

Interferencia

Contacto entre dientes que no sean en las partes previstas de sus superficies

Conjunto intercambiable

Un conjunto de engranajes, cualquiera de los cuales se acopla correctamente con cualquier otro.

Ángulo de hélice, ψ

Ángulo formado por una tangente a la hélice y el eje del engranaje. Es cero en el caso límite de un engranaje recto, aunque también puede considerarse como el ángulo de la hipotenusa.

Paso circular normal, p _n

Paso circular en el plano normal a los dientes.

Paso circular transversal, p

Paso circular en el plano de rotación del engranaje. A veces se lo denomina simplemente "paso circular".

${\displaystyle p_{n}=p\cos(\psi)}$

Se pueden observar otros parámetros de la hélice en el plano normal o en el plano transversal. El subíndice n suele indicar el plano normal.

Dirigir

Distancia desde cualquier punto de una rosca hasta el punto correspondiente en la siguiente vuelta de la misma rosca, medida paralelamente al eje.

Paso lineal, p

Distancia desde cualquier punto de una rosca hasta el punto correspondiente de la rosca adyacente, medida en paralelo al eje. Para un sinfín de una sola rosca, el paso de avance y el paso lineal son iguales.

Ángulo de avance, λ

Ángulo entre una tangente a la hélice y un plano perpendicular al eje. Nótese que el complemento del ángulo de la hélice se suele indicar para los engranajes helicoidales.

Diámetro de paso, d _w

Igual que lo descrito anteriormente en esta lista. Tenga en cuenta que, en el caso de un sinfín, se sigue midiendo en un plano perpendicular al eje del engranaje, no en un plano inclinado.

El subíndice w denota el gusano, el subíndice g denota el engranaje.

• 
  Línea de contacto
• 
  Camino de acción
• 
  Línea de acción
• 
  Plano de acción
• 
  Líneas de contacto (engranaje helicoidal)
• 
  Arco de acción
• 
  Duración de la acción
• 
  Diámetro límite
• 
  Avance de cara
• 
  Zona de acción

Punto de contacto

Cualquier punto en el que dos perfiles de dientes se tocan.

Línea de contacto

Una línea o curva a lo largo de la cual dos superficies dentales son tangentes entre sí.

Camino de acción

Lugar de los puntos de contacto sucesivos entre un par de dientes de engranaje, durante la fase de acoplamiento. En el caso de los dientes de engranaje conjugados, la trayectoria de acción pasa por el punto de paso. Es la traza de la superficie de acción en el plano de rotación.

Línea de acción

La trayectoria de acción de los engranajes evolventes es la línea recta que pasa por el punto de paso y es tangente a ambos círculos de base.

Superficie de acción

Superficie imaginaria en la que se produce el contacto entre dos superficies dentarias en contacto. Es la suma de las trayectorias de acción en todas las secciones de los dientes en contacto.

Plano de acción

Superficie de acción de los engranajes evolventes de ejes paralelos con dientes rectos o helicoidales. Es tangente a los cilindros de base.

Zona de acción (zona de contacto)

Para engranajes evolventes de ejes paralelos con dientes rectos o helicoidales, el área rectangular en el plano de acción está limitada por la longitud de acción y el ancho efectivo de la cara .

Ruta de contacto

La curva en cualquiera de las superficies de los dientes a lo largo de la cual se produce un contacto teórico de un solo punto durante el acoplamiento de engranajes con superficies de dientes abombadas o engranajes que normalmente se acoplan con un solo punto de contacto.

Duración de la acción

La distancia en la línea de acción a través de la cual se mueve el punto de contacto durante la acción del perfil del diente.

Arco de acción, Q _t

El arco del círculo primitivo a través del cual se mueve un perfil de diente desde el principio hasta el final del contacto con un perfil de acoplamiento.

Arco de aproximación, Q _a

El arco del círculo primitivo a través del cual se mueve un perfil de diente desde su inicio de contacto hasta que el punto de contacto llega al punto de paso.

Arco de receso, Q _r

El arco del círculo primitivo a través del cual se mueve un perfil de diente desde el contacto en el punto de paso hasta que finaliza el contacto.

Relación de contacto, m _c o ε

Número de pasos angulares que recorre la superficie de un diente desde el inicio hasta el final del contacto. De forma sencilla, se puede definir como una medida del número promedio de dientes en contacto durante el período en el que un diente entra y sale del contacto con el engranaje acoplado.

Relación de contacto transversal, m _p o ε _α

Relación de contacto en un plano transversal. Es la relación entre el ángulo de acción y el paso angular. En el caso de los engranajes evolventes, se obtiene de forma más directa como la relación entre la longitud de acción y el paso de base.

Relación de contacto facial, m _F o ε _β

Relación de contacto en un plano axial o relación entre el ancho de la cara y el paso axial. En el caso de los engranajes cónicos e hipoides, es la relación entre el avance de la cara y el paso circular.

Relación de contacto total, m _t o ε _γ

La suma de la relación de contacto transversal y la relación de contacto frontal.

${\displaystyle \epsilon _{\gamma }=\epsilon _{\alpha }+\epsilon _{\beta }}$

${\displaystyle m_{\rm {t}}=m_{\rm {p}}+m_{\rm {F}}}$

Relación de contacto modificada, m _o

Para engranajes cónicos, la raíz cuadrada de la suma de los cuadrados de las relaciones de contacto transversal y frontal.

${\displaystyle m_{\rm {o}}={\sqrt {m_{\rm {p}}^{2}+m_{\rm {F}}^{2}}}}$

Diámetro límite

Diámetro de un engranaje en el que la línea de acción intersecta el círculo de adición máximo (o mínimo en el caso de un piñón interno) del engranaje de acoplamiento. Esto también se conoce como inicio del perfil activo, inicio del contacto, final del contacto o final del perfil activo.

Inicio de perfil activo (SAP)

Intersección del diámetro límite y el perfil involuto.

Avance de cara

Distancia en un círculo primitivo a través de la cual un diente helicoidal o espiral se mueve desde la posición en la que comienza el contacto en un extremo de la traza del diente en la superficie primitiva hasta la posición donde cesa el contacto en el otro extremo.

• 
  Grosor del diente
• 
  Relaciones de espesor
• 
  Espesor de la cuerda
• 
  Medición del espesor de los dientes sobre pasadores
• 
  Medición de tramo
• 
  Dientes apéndices largos y cortos

Espesor circular

Longitud del arco entre los dos lados de un diente de engranaje, en el círculo de referencia especificado.

Espesor circular transversal

Espesor circular en el plano transversal.

Espesor circular normal

Espesor circular en el plano normal. En un engranaje helicoidal puede considerarse como la longitud del arco a lo largo de una hélice normal.

Espesor axial

En engranajes helicoidales y sinfines, espesor del diente en una sección transversal axial en el diámetro de paso estándar.

Espesor circular de la base

En dientes involutos, longitud del arco en el círculo base entre las dos curvas involutas que forman el perfil de un diente.

Espesor normal de la cuerda

Longitud de la cuerda que subtiende un arco de espesor circular en el plano normal a la hélice primitiva. Se puede seleccionar cualquier diámetro de medición conveniente, no necesariamente el diámetro primitivo estándar.

Adenda cordal (altura de la cuerda)

Altura desde la parte superior del diente hasta la cuerda que subtiende el arco de espesor circular. Se puede seleccionar cualquier diámetro de medición conveniente, no necesariamente el diámetro de paso estándar.

Cambio de perfil

Desplazamiento de la línea de referencia de la cremallera básica desde el cilindro de referencia, que se vuelve adimensional al dividirlo por el módulo normal. Se utiliza para especificar el espesor del diente, a menudo para que no haya juego.

Cambio de cremallera

Desplazamiento de la línea de referencia de la herramienta respecto del cilindro de referencia, que se vuelve adimensional al dividirlo por el módulo normal. Se utiliza para especificar el espesor del diente.

Medición sobre pines

Medición de la distancia tomada entre un pasador colocado en un espacio entre dientes y una superficie de referencia. La superficie de referencia puede ser el eje de referencia del engranaje, una superficie de referencia o uno o dos pasadores colocados en el espacio entre dientes o espacios opuestos al primero. Esta medición se utiliza para determinar el espesor del diente.

Medición de tramo

Medición de la distancia entre varios dientes en un plano normal. Siempre que el dispositivo de medición tenga superficies de medición paralelas que entren en contacto con una porción no modificada de la evolvente, la medición se realizará a lo largo de una línea tangente al cilindro base. Se utiliza para determinar el espesor de los dientes.

Dientes de adenda modificados

Dientes de engranajes engranados, uno o ambos de los cuales tienen un apéndice no estándar.

Dientes de profundidad completa

Dientes en los que la profundidad de trabajo es igual a 2.000 dividido por el paso diametral normal.

Dientes de muñón

Dientes en los que la profundidad de trabajo es inferior a 2.000 dividido por el paso diametral normal.

Dientes de adición iguales

Dientes en los que dos engranajes engranados tienen adendas iguales.

Dientes de apéndice largo y corto

Dientes en los que los apéndices de dos engranajes engranados son desiguales.

Vender a menor precio que

Un socavado es una condición en los dientes de engranaje generados cuando cualquier parte de la curva de filete se encuentra dentro de una línea trazada tangente al perfil de trabajo en su punto de unión con el filete. El socavado puede introducirse deliberadamente para facilitar las operaciones de acabado. Con el socavado, la curva de filete intersecta el perfil de trabajo. Sin el socavado, la curva de filete y el perfil de trabajo tienen una tangente común.

Filete de raíz

o curva de filete, la porción cóncava del perfil del diente donde se une a la parte inferior del espacio del diente.2

El paso es la distancia entre un punto de un diente y el punto correspondiente de un diente adyacente. ^[34] Es una dimensión medida a lo largo de una línea o curva en dirección transversal, normal o axial. El uso de la palabra paso sin calificación puede ser ambiguo y, por esta razón, es preferible utilizar designaciones específicas como paso circular transversal, paso de base normal o paso axial.

• 
  Paso
• 
  Paso de dientes
• 
  Relaciones de tono base
• 
  Principales lanzamientos

Paso circular, p

Distancia de arco a lo largo de un círculo primitivo o una línea primitiva especificada entre perfiles correspondientes de dientes adyacentes.

Paso circular transversal, p _t

Paso circular en el plano transversal.

Paso circular normal, p _n , p _e

Paso circular en el plano normal, y también longitud del arco a lo largo de la hélice de paso normal entre dientes o roscas helicoidales.

Paso axial, p _x

Paso lineal en un plano axial y en una superficie de paso. En los engranajes helicoidales y sinfines, el paso axial tiene el mismo valor en todos los diámetros. En los engranajes de otros tipos, el paso axial puede limitarse a la superficie de paso y puede ser una medida circular. Se prefiere el término paso axial al término paso lineal. El paso axial de un sinfín helicoidal y el paso circular de su engranaje sinfín son iguales.

Paso base normal, p _N , p _bn

Un engranaje helicoidal evolvente es el paso base en el plano normal. Es la distancia normal entre superficies helicoidales evolventes paralelas en el plano de acción en el plano normal, o es la longitud del arco en la hélice de base normal. Es una distancia constante en cualquier engranaje helicoidal evolvente.

Paso de base transversal, p _b , p _bt

En un engranaje evolvente, el paso se encuentra en el círculo de base o a lo largo de la línea de acción. Los lados correspondientes de los dientes del engranaje evolvente son curvas paralelas y el paso de base es la distancia constante y fundamental entre ellos a lo largo de una normal común en un plano transversal.

Paso diametral (transversal), P _d

Relación entre el número de dientes y el diámetro de paso estándar en pulgadas.

${\displaystyle P_{\rm {d}}={\frac {N}{d}}={\frac {25.4}{m}}={\frac {\pi }{p}}}$

Paso diametral normal, P _nd

Valor del paso diametral en un plano normal de un engranaje helicoidal o sinfín.

${\displaystyle P_{\rm {nd}}={\frac {P_{\rm {d}}}{\cos \psi }}}$

Paso angular, θ _N , τ

Ángulo subtendido por el paso circular, expresado habitualmente en radianes.

${\displaystyle \tau ={\frac {360}{z}}}$grados o radianes${\displaystyle {\frac {2\pi }{z}}}$

El juego es el error de movimiento que se produce cuando los engranajes cambian de dirección. Existe porque siempre hay un espacio entre la cara posterior del diente impulsor y la cara delantera del diente que se encuentra detrás de él en el engranaje impulsado, y ese espacio debe cerrarse antes de que se pueda transferir fuerza en la nueva dirección. El término "juego" también se puede utilizar para referirse al tamaño del espacio, no solo al fenómeno que causa; por lo tanto, se podría decir que un par de engranajes tiene, por ejemplo, "0,1 mm de juego". Un par de engranajes podría diseñarse para que no tuviera juego, pero esto presupondría perfección en la fabricación, características de expansión térmica uniformes en todo el sistema y ausencia de lubricante. Por lo tanto, los pares de engranajes están diseñados para tener algo de juego. Por lo general, se consigue reduciendo el grosor de los dientes de cada engranaje a la mitad de la distancia de espacio deseada. Sin embargo, en el caso de un engranaje grande y un piñón pequeño, el juego suele eliminarse por completo del engranaje y se le dan al piñón dientes de tamaño completo. El juego también se puede conseguir separando más los engranajes. El juego de un tren de engranajes es igual a la suma del juego de cada par de engranajes, por lo que en trenes largos el juego puede convertirse en un problema.

En situaciones que requieren precisión, como la instrumentación y el control, el juego puede minimizarse mediante una de varias técnicas. Por ejemplo, el engranaje puede dividirse a lo largo de un plano perpendicular al eje, una mitad fijada al eje de la manera habitual, la otra mitad colocada a lo largo de él, libre para girar alrededor del eje, pero con resortes entre las dos mitades que proporcionan un par relativo entre ellas, de modo que se logra, en efecto, un solo engranaje con dientes expansibles. Otro método implica estrechar los dientes en la dirección axial y dejar que el engranaje se deslice en la dirección axial para compensar la holgura.

Aunque los engranajes pueden fabricarse con cualquier paso, por conveniencia e intercambiabilidad se utilizan con frecuencia pasos estándar. El paso es una propiedad asociada con las dimensiones lineales y, por lo tanto, difiere si los valores estándar están en el sistema imperial (pulgadas) o métrico . Utilizando medidas en pulgadas , se eligen valores de paso diametral estándar con unidades de "por pulgada"; el paso diametral es el número de dientes en un engranaje de un diámetro de paso de una pulgada. Los valores estándar comunes para engranajes rectos son 3, 4, 5, 6, 8, 10, 12, 16, 20, 24, 32, 48, 64, 72, 80, 96, 100, 120 y 200. ^[55] Ciertos pasos estándar, como 1 ⁄ 10 y 1 ⁄ 20 en medidas de pulgada, que encajan con la cremallera lineal, son en realidad valores de paso circular (lineal) con unidades de "pulgadas" ^[55]

Cuando las dimensiones de los engranajes están en el sistema métrico, la especificación del paso generalmente se hace en términos de módulo o módulo , que es efectivamente una medida de longitud a lo largo del diámetro de paso . El término módulo se entiende como el diámetro de paso en milímetros dividido por el número de dientes. Cuando el módulo se basa en medidas en pulgadas, se conoce como módulo inglés para evitar confusiones con el módulo métrico. El módulo es una dimensión directa ("milímetros por diente"), a diferencia del paso diametral, que es una dimensión inversa ("dientes por pulgada"). Por lo tanto, si el diámetro de paso de un engranaje es de 40 mm y el número de dientes es de 20, el módulo es 2, lo que significa que hay 2 mm de diámetro de paso para cada diente. ^[56] Los valores de módulo estándar preferidos son 0,1, 0,2, 0,3, 0,4, 0,5, 0,6, 0,8, 1,0, 1,25, 1,5, 2,0, 2,5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40 y 50. ^[57]

La física moderna adoptó el modelo de engranajes de diferentes maneras. En el siglo XIX, James Clerk Maxwell desarrolló un modelo de electromagnetismo en el que las líneas de campo magnético eran tubos giratorios de fluido incompresible. Maxwell utilizó una rueda dentada y la llamó "rueda loca" para explicar la corriente eléctrica como una rotación de partículas en direcciones opuestas a la de las líneas de campo giratorias. ^[58]

Más recientemente, la física cuántica utiliza en su modelo "engranajes cuánticos". Un grupo de engranajes puede servir como modelo para varios sistemas diferentes, como un dispositivo nanomecánico construido artificialmente o un grupo de moléculas en forma de anillo. ^[59]

La hipótesis de las tres ondas compara la dualidad onda-partícula con un engranaje cónico. ^[60]

El mecanismo de engranajes se consideraba anteriormente exclusivamente artificial, pero ya en 1957, se habían reconocido engranajes en las patas traseras de varias especies de chicharritas ^[61] y científicos de la Universidad de Cambridge caracterizaron su importancia funcional en 2013 al realizar fotografías de alta velocidad de las ninfas de Issus coleoptratus en la Universidad de Cambridge. ^{[62] [63]} Estos engranajes se encuentran solo en las formas de ninfa de todas las chicharritas, y se pierden durante la muda final a la etapa adulta. ^[64] En I. coleoptratus , cada pata tiene una tira de dientes de 400 micrómetros, un radio de paso de 200 micrómetros, con 10 a 12 dientes de engranaje de tipo espolón completamente entrelazados, incluidas curvas fileteadas en la base de cada diente para reducir el riesgo de cizallamiento. ^[65] La articulación gira como engranajes mecánicos y sincroniza las patas traseras de Issus cuando salta con una precisión de 30 microsegundos, lo que evita la rotación de guiñada. ^{[66] [67] [62]} Los engranajes no están conectados todo el tiempo. Uno está ubicado en cada una de las patas traseras del insecto juvenil, y cuando se prepara para saltar, los dos juegos de dientes se bloquean entre sí. Como resultado, las patas se mueven casi al unísono, lo que le da al insecto más potencia a medida que los engranajes giran hasta su punto de parada y luego se desbloquean. ^[66]

• Caja de cambios
• Rueda de espigas
• Diferencial
• Principio de superposición
• Cadena cinemática

Bibliografía

• McGraw-Hill (2007), Enciclopedia McGraw-Hill de Ciencia y Tecnología (10.ª ed.), McGraw-Hill Professional, ISBN 978-0-07-144143-8.
• Norton, Robert L. (2004), Diseño de maquinaria (3.ª ed.), McGraw-Hill Professional, ISBN 978-0-07-121496-4.
• Vallance, Alex; Doughtie, Venton Levy (1964), Diseño de miembros de máquinas (4ª ed.), McGraw-Hill.
• Prensa industrial (2012), Manual de maquinaria (29.ª edición), ISBN 978-0-8311-2900-2 
• Ingenieros Edge, diseño de engranajes y datos de ingeniería.

• Asociación Estadounidense de Fabricantes de Engranajes ; Instituto Nacional Estadounidense de Normas (2005), Nomenclatura de engranajes: definiciones de términos con símbolos (ANSI/AGMA 1012-F90 ed.), Asociación Estadounidense de Fabricantes de Engranajes, ISBN 978-1-55589-846-5.
• Buckingham, Earle (1949), Mecánica analítica de engranajes , McGraw-Hill Book Co..
• Coy, John J.; Townsend, Dennis P.; Zaretsky, Erwin V. (1985), Gearing (PDF) , División de Información Científica y Técnica de la NASA , NASA-RP-1152; Informe técnico AVSCOM 84-C-15.
• Kravchenko AI, Bovda AM Engranaje con par magnético. Patente de Ucrania N. 56700 – Bul. N. 2, 2011 – F16H 49/00.
• Sclater, Neil. (2011). "Engranajes: dispositivos, accionamientos y mecanismos". Mecanismos y dispositivos mecánicos. Libro de consulta. 5.ª ed. Nueva York: McGraw Hill. pp. 131–174. ISBN 9780071704427. Dibujos y diseños de varios engranajes. 
• "Ruedas que no pueden patinar". Popular Science , febrero de 1945, págs. 120-125.

Wikimedia Commons tiene medios relacionados con Engranajes.

• Geararium. Museo de engranajes y ruedas dentadas: engranajes antiguos y vintage, ruedas dentadas, carracas y otros objetos relacionados con los engranajes.
• Biblioteca digital de modelos cinemáticos para el diseño (KMODDL): películas y fotografías de cientos de modelos en funcionamiento en la Universidad de Cornell
• Breve relato histórico sobre la aplicación de la geometría analítica a la forma de los dientes de los engranajes
• Tutorial matemático sobre engranajes (relacionado con la robótica)
• Asociación Estadounidense de Fabricantes de Engranajes
• Gear Technology, la revista especializada en fabricación de engranajes