Punto de Misiurewicz

En matemáticas , un punto de Misiurewicz es un valor de parámetro en el conjunto de Mandelbrot (el espacio de parámetros de las aplicaciones cuadráticas complejas ) y también en aplicaciones cuadráticas reales del intervalo ^[1] para las que el punto crítico es estrictamente preperiódico (es decir, se vuelve periódico después de un número finito de iteraciones pero no es periódico en sí mismo). Por analogía, el término punto de Misiurewicz también se utiliza para parámetros en un conjunto multibrot donde el único punto crítico es estrictamente preperiódico. Este término tiene menos sentido para las aplicaciones en mayor generalidad que tienen más de un punto crítico libre porque algunos puntos críticos pueden ser periódicos y otros no. Estos puntos reciben su nombre del matemático polaco-estadounidense Michał Misiurewicz , quien fue el primero en estudiarlos. ^[2]

Un parámetro es un punto de Misiurewicz si satisface las ecuaciones:${\estilo de visualización c}$$Estilo de visualización M_{k,n}$

${\displaystyle f_{c}^{(k)}(z_{cr})=f_{c}^{(k+n)}(z_{cr})}$

y:

${\displaystyle f_{c}^{(k-1)}(z_{cr})\neq f_{c}^{(k+n-1)}(z_{cr})}$

entonces:

${\displaystyle M_{k,n}=c:f_{c}^{(k)}(z_{cr})=f_{c}^{(k+n)}(z_{cr})}$

dónde:

• ${\displaystyle z_{cr}}$es un punto crítico de ,$Estilo de visualización f_{c}$
• ${\estilo de visualización k}$y son números enteros positivos,${\estilo de visualización n}$
• ${\displaystyle f_{c}^{(k)}}$denota la -ésima iteración de .${\estilo de visualización k}$$Estilo de visualización f_{c}$

El término "punto de Misiurewicz" se utiliza de forma ambigua: Misiurewicz investigó originalmente mapas en los que todos los puntos críticos eran no recurrentes; es decir, en los que existe un entorno para cada punto crítico que no es visitado por la órbita de este punto crítico. Este significado está firmemente establecido en el contexto de la dinámica de los mapas de intervalos iterados. ^[3] Solo en casos muy especiales un polinomio cuadrático tiene un punto crítico estrictamente periódico y único. En este sentido restringido, el término se utiliza en dinámica compleja; un sentido más apropiado sería puntos de Misiurewicz-Thurston (en honor a William Thurston , quien investigó mapas racionales finitos poscríticos).

Un polinomio cuadrático complejo tiene un solo punto crítico. Mediante una conjugación adecuada , cualquier polinomio cuadrático puede transformarse en una función de la forma que tiene un único punto crítico en . Los puntos de Misiurewicz de esta familia de funciones son raíces de las ecuaciones:${\displaystyle P_{c}(z)=z^{2}+c}$${\displaystyle z=0}$

${\displaystyle P_{c}^{(k)}(0)=P_{c}^{(k+n)}(0),}$

Sujeto a la condición de que el punto crítico no sea periódico, donde:

• k es el pre-periodo
• n es el periodo
• ${\displaystyle P_{c}^{(n)}=P_{c}(P_{c}^{(n-1)})}$denota la composición n -vez de consigo mismo, es decir, la n- ^ésima iteración de .${\displaystyle P_{c}(z)=z^{2}+c}$ $Estilo de visualización P_{c}$

Por ejemplo, los puntos de Misiurewicz con k = 2 y n = 1, denotados por M _2,1 , son raíces de:

${\displaystyle {\begin{aligned}&P_{c}^{(2)}(0)=P_{c}^{(3)}(0)\\\Rightarrow {}&c^{2}+c=(c^{2}+c)^{2}+c\\\Rightarrow {}&c^{4}+2c^{3}=0.\end{aligned}}}$

La raíz c = 0 no es un punto de Misiurewicz porque el punto crítico es un punto fijo cuando c = 0 y, por lo tanto, es periódico en lugar de preperiódico. Esto deja un único punto de Misiurewicz M _2,1 en c = −2.

Los puntos de Misiurewicz pertenecen y son densos en el límite del conjunto de Mandelbrot. ^{[4] [5]}

Si es un punto de Misiurewicz, entonces el conjunto de Julia lleno asociado es igual al conjunto de Julia y significa que el conjunto de Julia lleno no tiene interior .${\estilo de visualización c}$

Si es un punto de Misiurewicz, entonces en el conjunto de Julia correspondiente todos los ciclos periódicos son repulsivos (en particular el ciclo en el que cae la órbita crítica).${\estilo de visualización c}$

El conjunto de Mandelbrot y el conjunto de Julia son localmente asintóticamente autosimilares alrededor de los puntos de Misiurewicz. ^[6]$Estilo de visualización J_{c}}$

Los puntos de Misiurewicz en el contexto del conjunto de Mandelbrot se pueden clasificar en función de varios criterios. Uno de ellos es el número de rayos externos que convergen en dicho punto. ^[4] Los puntos de ramificación, que pueden dividir el conjunto de Mandelbrot en dos o más subregiones, tienen tres o más argumentos externos (o ángulos) . Los puntos que no son de ramificación tienen exactamente dos rayos externos (estos corresponden a puntos que se encuentran en arcos dentro del conjunto de Mandelbrot). Estos puntos que no son de ramificación son generalmente más sutiles y difíciles de identificar en representaciones visuales. Los puntos finales, o puntas de las ramas, tienen solo un rayo externo que converge en ellos. Otro criterio para clasificar los puntos de Misiurewicz es su aparición dentro de un gráfico de un subconjunto del conjunto de Mandelbrot. Los puntos de Misiurewicz se pueden encontrar en los centros de espirales, así como en los puntos donde se encuentran dos o más ramas. ^[7] Según el Teorema de la Rama del conjunto de Mandelbrot, ^[5] todos los puntos de ramificación del conjunto de Mandelbrot son puntos de Misiurewicz. ^{[4] [5]}

La mayoría de los parámetros de Misiurewicz dentro del conjunto de Mandelbrot exhiben un "centro de espiral". ^[8] Esto ocurre debido al comportamiento en un parámetro de Misiurewicz donde el valor crítico salta a un ciclo periódico de repulsión después de un número finito de iteraciones. En cada punto durante el ciclo, el conjunto de Julia exhibe autosimilitud asintótica a través de la multiplicación compleja por la derivada de este ciclo. Si la derivada no es real, implica que el conjunto de Julia cerca del ciclo periódico tiene una estructura espiral. En consecuencia, una estructura espiral similar ocurre en el conjunto de Julia cerca del valor crítico, y por el teorema de Tan Lei , también en el conjunto de Mandelbrot cerca de cualquier parámetro de Misiurewicz para el cual la órbita de repulsión tiene un multiplicador no real. La visibilidad de la forma espiral depende del valor de este multiplicador. El número de brazos en la espiral corresponde al número de ramas en el parámetro de Misiurewicz, que a su vez es igual al número de ramas en el valor crítico en el conjunto de Julia. Incluso el punto principal de Misiurewicz en el tercio de rama, ubicado al final de los rayos paramétricos en los ángulos 9/56, 11/56 y 15/56, es asintóticamente una espiral con infinitas vueltas, aunque esto es difícil de discernir sin aumento. ^{[ cita requerida ]}

Los argumentos externos de los puntos de Misiurewicz, medidos en turnos , son:

• Números racionales
• Fracciones propias con denominador par
  • Fracciones diádicas con denominador y expansión finita ( terminal ):${\displaystyle =2^{b}}$$${\displaystyle {\frac {1}{2}}_{10}=0.5_{10}=0.1_{2}}$$
  • Fracciones con denominador y expansión repetida : ^[9]${\displaystyle =a\cdot 2^{b}}$ $${\displaystyle {\frac {1}{6}}_{10}={\frac {1}{2\times 3}}_{10}=0,16666..._{10}=0,0(01)..._{2}.}$$

donde: a y b son números enteros positivos y b es impar, el número subíndice muestra la base del sistema numérico .

El punto se considera un punto final ya que es la punta de un filamento, ^[10] y el punto de aterrizaje del rayo externo para el ángulo 1/6. Su órbita crítica es . ^[11]$estilo de visualización c=M_{2,2}=i}$${\displaystyle \{0,i,i-1,-i,i-1,-i...\}}$

El punto se considera un punto final ya que es el punto final de la antena principal del conjunto de Mandelbrot. ^[12] y el punto de aterrizaje de un solo rayo externo (rayo de parámetro) de ángulo 1/2. También se considera un punto final porque su órbita crítica es , ^[11] siguiendo la secuencia simbólica = CLRRR ... con un preperiodo de 2 y un periodo de 1.$estilo de visualización c=M_{2,1}=-2}$${\displaystyle \{0,-2,2,2,2,...\}}$

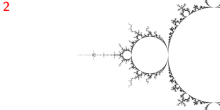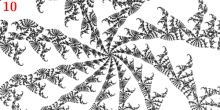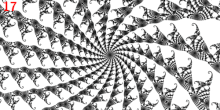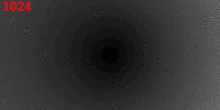
El punto se considera un punto de ramificación porque es un punto principal de Misiurewicz del limbo 1/3 y tiene 3 rayos externos: 9/56, 11/56 y 15/56.${\displaystyle c=-0,10109636384562...+i\,0,95628651080914...=M_{4,1}}$

Se trata de puntos que no son ramificaciones ni puntos finales.

El punto está cerca de un punto de Misiurewicz . Esto se puede ver porque es el centro de una espiral de dos brazos, el punto de aterrizaje de dos rayos externos con ángulos: y donde el denominador es , y tiene un punto preperiódico con preperiodo y periodo .${\displaystyle c=-0.77568377+i\,0.13646737}$$Estilo de visualización M_{23,2}$${\displaystyle {\frac {8388611}{25165824}}}$${\displaystyle {\frac {8388613}{25165824}}}$$Estilo de visualización 3*2^{23}}$${\estilo de visualización k=23}$${\estilo de visualización n=2}$

El punto está cerca de un punto Misiurewicz , ya que es el punto de aterrizaje de un par de rayos: , y tiene preperiodo y período .${\displaystyle c=-1.54368901269109}$$Estilo de visualización M_{3,1}$${\displaystyle {\frac {5}{12}}}$${\displaystyle {\frac {7}{12}}}$${\displaystyle k=3}$${\estilo de visualización n=1}$

• Dinámica aritmética
• Punto de Feigenbaum
• Dendrita (matemáticas)

Wikilibros tiene un libro sobre el tema: Fractales

• Puntos preperiódicos (Misiurewicz) en el conjunto de Mandelbrot de Evgeny Demidov
• Similitud de conjuntos M y J para puntos preperiódicos. Teorema de Lei de Douglas C. Ravenel
• Punto Misiurewicz del mapa logístico de JC Sprott