Necesidad y suficiencia

En lógica y matemáticas , necesidad y suficiencia son términos utilizados para describir una relación condicional o implicacional entre dos enunciados . Por ejemplo, en el enunciado condicional : "Si P entonces Q ", Q es necesaria para P , porque la verdad de Q está garantizada por la verdad de P. (Equivalentemente, es imposible tener P sin Q , o la falsedad de Q asegura la falsedad de P. ) ^[1] De manera similar, P es suficiente para Q , porque el hecho de que P sea verdadero siempre implica que Q es verdadero, pero el hecho de que P no sea verdadero no siempre implica que Q no sea verdadero. ^[2]

En general, una condición necesaria es aquella (posiblemente una de varias condiciones) que debe estar presente para que ocurra otra condición, mientras que una condición suficiente es aquella que produce dicha condición. ^[3] La afirmación de que un enunciado es una condición "necesaria y suficiente" de otro significa que el primer enunciado es verdadero si y solo si el segundo es verdadero. Es decir, los dos enunciados deben ser simultáneamente verdaderos o simultáneamente falsos. ^{[4] [5] [6]}

En inglés corriente (también lenguaje natural ) "necesario" y "suficiente" indican relaciones entre condiciones o estados de cosas, no enunciados. Por ejemplo, ser hombre es una condición necesaria para ser hermano, pero no es suficiente, mientras que ser hombre hermano es una condición necesaria y suficiente para ser hermano. Cualquier enunciado condicional consta de al menos una condición suficiente y al menos una condición necesaria.

En el análisis de datos , la necesidad y la suficiencia pueden referirse a diferentes lógicas causales , ^[7] donde el análisis de condiciones necesarias y el análisis comparativo cualitativo pueden usarse como técnicas analíticas para examinar la necesidad y la suficiencia de las condiciones para un resultado particular de interés.

En el enunciado condicional "si S , entonces N ", la expresión representada por S se denomina antecedente y la expresión representada por N se denomina consecuente . Este enunciado condicional puede escribirse de varias formas equivalentes, como " N si S ", " S sólo si N ", " S implica N ", " N está implícito en S ", S → N , S ⇒ N y " N siempre que S ". ^[8]

En la situación anterior de "N siempre que S", se dice que N es una condición necesaria para S. En lenguaje común, esto es equivalente a decir que si el enunciado condicional es un enunciado verdadero, entonces el consecuente N debe ser verdadero, si S ha de ser verdadero (véase la tercera columna de la " tabla de verdad " inmediatamente debajo). En otras palabras, el antecedente S no puede ser verdadero sin que N sea verdadero. Por ejemplo, para que alguien se llame Sócrates , es necesario que ese alguien sea Nom bre. De manera similar, para que los seres humanos vivan, es necesario que tengan aire. ^[9]

También se puede decir que S es una condición suficiente para N (consulte nuevamente la tercera columna de la tabla de verdad que aparece inmediatamente debajo). Si el enunciado condicional es verdadero, entonces si S es verdadero, N debe ser verdadero; mientras que si el enunciado condicional es verdadero y N es verdadero, entonces S puede ser verdadero o falso. En términos comunes, "la verdad de S garantiza la verdad de N ". ^[9] Por ejemplo, siguiendo con el ejemplo anterior, se puede decir que saber que alguien se llama Sócrates es suficiente para saber que alguien tiene un Nombre .

Una condición necesaria y suficiente requiere que se cumplan ambas implicaciones y (la última de las cuales también puede escribirse como ). La primera implicación sugiere que S es una condición suficiente para N , mientras que la segunda implicación sugiere que S es una condición necesaria para N . Esto se expresa como " S es necesario y suficiente para N ", " S si y solo si N ", o .${\displaystyle S\Flecha derecha N}$${\displaystyle N\Flecha derecha S}$${\displaystyle S\Flecha izquierda N}$ ${\displaystyle S\Flecha izquierda derecha N}$

Tabla de verdad

S	norte	${\displaystyle S\Flecha derecha N}$	${\displaystyle S\Flecha izquierda N}$	${\displaystyle S\Flecha izquierda derecha N}$
yo	yo	yo	yo	yo
yo	F	F	yo	F
F	yo	yo	F	F
F	F	yo	yo	yo

La afirmación de que Q es necesaria para P es coloquialmente equivalente a " P no puede ser verdadero a menos que Q sea verdadero" o "si Q es falso, entonces P es falso". ^{[9] [1]} Por contraposición , esto es lo mismo que "siempre que P es verdadero, también lo es Q ".

La relación lógica entre P y Q se expresa como "si P , entonces Q " y se denota " P ⇒ Q " ( P implica Q ). También puede expresarse como cualquiera de " P sólo si Q ", " Q , si P ", " Q siempre que P " y " Q cuando P ". A menudo se encuentran, en la prosa matemática, por ejemplo, varias condiciones necesarias que, tomadas en conjunto, constituyen una condición suficiente (es decir, individualmente necesarias y conjuntamente suficientes ^[9] ), como se muestra en el Ejemplo 5.

Ejemplo 1

Para que sea verdad que "Juan es soltero", es necesario que también sea verdad que es

1. soltero,
2. masculino,
3. adulto,

ya que afirmar "Juan es soltero" implica que Juan tiene cada uno de esos tres predicados adicionales .

Ejemplo 2

Para los números enteros mayores que dos, es necesario ser impar para ser primo, ya que dos es el único número entero que es a la vez par y primo.

Ejemplo 3

Consideremos el trueno, el sonido causado por el relámpago. Se dice que el trueno es necesario para el relámpago, ya que el relámpago nunca se produce sin truenos. Siempre que hay relámpago, hay trueno. El trueno no causa el relámpago (ya que el relámpago causa truenos), pero como el relámpago siempre viene con el trueno, decimos que el trueno es necesario para el relámpago. (Es decir, en su sentido formal, la necesidad no implica causalidad).

Ejemplo 4

Para ser senador de Estados Unidos es necesario tener al menos 30 años. Si tienes menos de 30 años, no podrás ser senador. Es decir, si eres senador, se deduce que debes tener al menos 30 años.

Ejemplo 5

En álgebra , para algún conjunto S junto con una operación para formar un grupo , es necesario que Failed to parse (SVG (MathML se puede habilitar a través del complemento del navegador): respuesta no válida ("La extensión Math no puede conectarse a Restbase") del servidor "http://localhost:6011/en.wikipedia.org/v1/":): {\displaystyle \star} sea asociativo . También es necesario que S incluya un elemento especial e tal que para cada x en S , sea el caso de que e x y x e sean ambos iguales a x . También es necesario que para cada x en S exista un elemento correspondiente x″ , tal que tanto x x″ como x″ x sean iguales al elemento especial e . Ninguna de estas tres condiciones necesarias por sí sola es suficiente, pero la conjunción de las tres sí lo es.${\estilo de visualización \estrella}$ ${\estilo de visualización \estrella}$ ${\estilo de visualización \estrella}$ ${\estilo de visualización \estrella}$ ${\estilo de visualización \estrella}$

Si P es suficiente para Q , entonces saber que P es verdadero es motivo adecuado para concluir que Q es verdadero; sin embargo, saber que P es falso no satisface una necesidad mínima para concluir que Q es falso.

La relación lógica se expresa, como antes, como "si P , entonces Q " o " P ⇒ Q ". Esto también se puede expresar como " P sólo si Q ", " P implica Q " o varias otras variantes. Puede darse el caso de que varias condiciones suficientes, tomadas en conjunto, constituyan una única condición necesaria (es decir, individualmente suficientes y conjuntamente necesarias), como se ilustra en el ejemplo 5.

Ejemplo 1

"Juan es un rey" implica que Juan es un hombre. Por lo tanto, saber que Juan es un rey es suficiente para saber que es un hombre.

Ejemplo 2

Que un número sea divisible por 4 es suficiente (pero no necesario) para que sea par, pero que sea divisible por 2 es suficiente y necesario para que sea par.

Ejemplo 3

La ocurrencia de un trueno es condición suficiente para la ocurrencia de un rayo en el sentido de que oír un trueno y reconocerlo inequívocamente como tal justifica concluir que ha habido un rayo.

Ejemplo 4

Si el Congreso de los Estados Unidos aprueba un proyecto de ley, basta con que el presidente lo firme para que se convierta en ley. Cabe señalar que el caso en el que el presidente no haya firmado el proyecto de ley, por ejemplo, mediante el ejercicio de un veto presidencial , no significa que el proyecto de ley no se haya convertido en ley (por ejemplo, podría haberse convertido en ley mediante una anulación del Congreso ).

Ejemplo 5

Para que una carta sea un as es suficiente que el centro de la misma esté marcado con una sola espada grande (♠). Otras tres condiciones suficientes son que el centro de la carta esté marcado con un solo diamante (♦), corazón (♥) o trébol (♣). Ninguna de estas condiciones es necesaria para que la carta sea un as, pero sí lo es su disyunción , ya que ninguna carta puede ser un as sin cumplir al menos (de hecho, exactamente) una de estas condiciones.

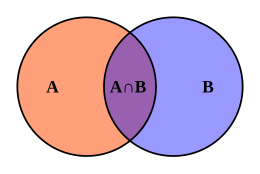
Una condición puede ser necesaria o suficiente sin ser la otra. Por ejemplo, ser un mamífero ( N ) es necesario pero no suficiente para ser un humano ( S ), y que un número sea racional ( S ) es suficiente pero no necesario para ser un número real ( N ) (ya que hay números reales que no son racionales).${\estilo de visualización x}$ ${\estilo de visualización x}$

Una condición puede ser necesaria y suficiente. Por ejemplo, en la actualidad, "hoy es el 4 de julio " es una condición necesaria y suficiente para "hoy es el Día de la Independencia de los Estados Unidos ". De manera similar, una condición necesaria y suficiente para la invertibilidad de una matriz M es que M tenga un determinante distinto de cero .

Matemáticamente hablando, la necesidad y la suficiencia son duales entre sí. Para cualquier enunciado S y N , la afirmación de que " N es necesario para S " es equivalente a la afirmación de que " S es suficiente para N ". Otra faceta de esta dualidad es que, como se ilustró anteriormente, las conjunciones (usando "y") de condiciones necesarias pueden lograr la suficiencia, mientras que las disyunciones (usando "o") de condiciones suficientes pueden lograr la necesidad. Para una tercera faceta, identifique cada predicado matemático N con el conjunto T ( N ) de objetos, eventos o enunciados para los cuales N es verdadero; entonces, afirmar la necesidad de N para S es equivalente a afirmar que T ( N ) es un superconjunto de T ( S ), mientras que afirmar la suficiencia de S para N es equivalente a afirmar que T ( S ) es un subconjunto de T ( N ).

Desde el punto de vista psicológico, la necesidad y la suficiencia son aspectos clave de la concepción clásica de los conceptos. Según la teoría clásica de los conceptos, la forma en que las mentes humanas representan una categoría X da lugar a un conjunto de condiciones individualmente necesarias que definen X. En conjunto, estas condiciones individualmente necesarias son suficientes para ser X. ^[10] Esto contrasta con la teoría probabilística de los conceptos, que afirma que ninguna característica definitoria es necesaria o suficiente, sino que las categorías se asemejan a una estructura de árbol genealógico.

Decir que P es necesario y suficiente para Q es decir dos cosas:

1. que P es necesario para Q , , y que P es suficiente para Q , .${\displaystyle P\Flecha izquierda Q}$${\displaystyle P\Flecha derecha Q}$
2. de manera equivalente, se puede entender que P y Q son necesarios el uno para el otro, lo que también se puede afirmar como que cada uno es suficiente para el otro o implica al otro.${\displaystyle P\Flecha derecha Q\land Q\Flecha derecha P}$

Se pueden resumir cualquiera, y por lo tanto todos, estos casos mediante la afirmación " P si y sólo si Q ", que se denota por , mientras que los casos nos dicen que es idéntico a .${\displaystyle P\Flecha izquierda derecha Q}$${\displaystyle P\Flecha izquierda derecha Q}$${\displaystyle P\Flecha derecha Q\land Q\Flecha derecha P}$

Por ejemplo, en teoría de grafos, un grafo G se llama bipartito si es posible asignar a cada uno de sus vértices el color negro o blanco de tal manera que cada arista de G tenga un extremo de cada color. Y para que cualquier grafo sea bipartito, es una condición necesaria y suficiente que no contenga ciclos de longitud impar . Por lo tanto, descubrir si un grafo tiene ciclos impares nos dice si es bipartito y viceversa. Un filósofo ^[11] podría caracterizar este estado de cosas así: "Aunque los conceptos de bipartidismo y ausencia de ciclos impares difieren en intención , tienen idéntica extensión ". ^[12]

En matemáticas, los teoremas a menudo se enuncian en la forma " P es verdadero si y sólo si Q es verdadero".

Porque, como se explicó en la sección anterior, la necesidad de uno para el otro es equivalente a la suficiencia del otro para el primero, es decir, es equivalente a , si P es necesario y suficiente para Q , entonces Q es necesario y suficiente para P . Podemos escribir y decir que las afirmaciones " P es verdadero si y solo si Q , es verdadero" y " Q es verdadero si y solo si P es verdadero" son equivalentes.${\displaystyle P\Flecha izquierda Q}$ ${\displaystyle Q\Flecha derecha P}$${\displaystyle P\Flecha izquierda derecha Q\equiv Q\Flecha izquierda derecha P}$

Wikimedia Commons tiene medios relacionados con Necesidad y suficiencia .

• Tutorial web de pensamiento crítico: Condiciones necesarias y suficientes
• Universidad Simon Fraser: conceptos y ejemplos