Octagrama
| Octagrama regular | |
|---|---|
 Un octagrama regular | |
| Tipo | Polígono estrellado regular |
| Aristas y vértices | 8 |
| Símbolo de Schläfli | {8/3} y{4/3} |
| Diagramas de Coxeter-Dynkin |       |
| Grupo de simetría | Diédrico (D 8 ) |
| Angulo interno ( grados ) | 45° |
| Propiedades | estrella , cíclica , equilátera , isogonal , isotoxal |
| Polígono dual | ser |
| Polígonos estelares |
|---|
En geometría , un octagrama es un polígono estrellado de ocho ángulos .
El nombre octagrama combina el prefijo numeral griego octa- con el sufijo griego -gramo . El sufijo -gramo deriva de γραμμή ( grammḗ ) que significa "línea". [1]
Detalle
En general, un octagrama es cualquier octógono ( polígono de 8 lados ) que se interseca consigo mismo.
El octagrama regular está marcado con el símbolo Schläfli {8/3}, que significa una estrella de 8 lados, conectados por cada tercer punto.
Variaciones
Estas variaciones tienen una simetría diedro inferior, Dih 4 :
 Angosto  Amplio (rotación de 45 grados) |   Isotoxal |  Una antigua bandera de Chile contenía esta geometría de estrella octogonal con los bordes eliminados (el Guñelve ). |  La estrella octogonal regular es muy popular como símbolo de los clubes de remo de la región de Baja Colonia , como se ve en la bandera del club de remo de Colonia . |  La geometría se puede ajustar para que tres bordes se crucen en un solo punto, como el símbolo de Auseklis. |  Una rosa de los vientos de 8 puntas puede verse como una estrella octogonal, con 4 puntas primarias y 4 puntas secundarias. |
El símbolo Rub el Hizb es un glifo Unicode ۞ en U+06DE.
Como un cuadrado cuasi truncado
Truncamientos más profundos del cuadrado pueden producir formas poligonales isogonales (transitivas de vértice) intermedias con vértices espaciados de manera uniforme y dos longitudes de arista. Un cuadrado truncado es un octágono, t{4}={8}. Un cuadrado cuasitruncado, invertido como {4/3}, es un octagrama, t{4/3}={8/3}. [2]
El poliedro estrellado uniforme hexaedro truncado estrellado , t'{4,3}=t{4/3,3} tiene caras de octagrama construidas a partir del cubo de esta manera. Por esta razón, puede considerarse un análogo tridimensional del octagrama.
| Regular | Cuasiregular | Isogonal | Cuasiregular |
|---|---|---|---|
 {4} |  t{4}={8} |  | 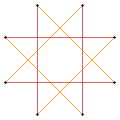 t'{4}=t{4/3}={8/3} |
| Regular | Uniforme | Isogonal | Uniforme |
 {4,3} |  t{4,3} |  |  t'{4,3}=t{4/3,3} |
Otra versión tridimensional del octagrama es el gran rombicuboctaedro no convexo (cuasirrombicuboctaedro), que puede considerarse como un cubo cuasicantelado (cuasiexpandido), t 0,2 {4/3,3}.
Compuestos de polígonos estelares
Existen dos figuras estelares octagrámicas regulares (compuestas) de la forma {8/k}, la primera construida como dos cuadrados {8/2}=2{4}, y la segunda como cuatro dígonos degenerados , {8/4}=4{2}. Existen otros compuestos isogonales e isotoxales que incluyen formas rectangulares y rómbicas.
| Regular | Isogonal | Isotoxal | ||
|---|---|---|---|---|
.svg/1280px-Regular_star_figure_2(4,1).svg.png) un{8}={8/2}=2{4} | .svg/1280px-Regular_star_figure_4(2,1).svg.png) {8/4}=4{2} |  |  |  |
.svg){kind=link}
.svg){kind=link}
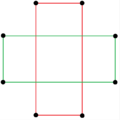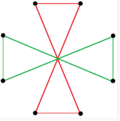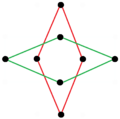{8/2} o 2{4}, como los diagramas de Coxeter +, puede verse como el equivalente 2D del compuesto 3D del cubo y el octaedro ,
+, compuesto 4D de tesseract y 16 celdas,+y compuesto 5D de 5-cubo y 5-ortoplex ; es decir, el compuesto de un n-cubo y un politopo cruzado en sus respectivas posiciones duales.
Otras presentaciones de una estrella octogonal
Una estrella octogonal puede verse como un hexadecágono cóncavo , con la geometría de intersección interna borrada. También puede diseccionarse mediante líneas radiales.
| polígono estrellado | Cóncavo | Disecciones centrales | ||
|---|---|---|---|---|
 Compuesto 2{4} |  |8/2| |  |  |  |
 Regular {8/3} |  |8/3| |  |  |  |
 Isogonal |  |  |  |  |
 Isotoxal |  |  |  |  |
Otros usos
_Commissioning_Image_(jupiter-hi-res-rings).tiff/lossless-page1-1280px-Jupiter%E2%80%99s_Rings_And_Moons_(NIRCam)_Commissioning_Image_(jupiter-hi-res-rings).tiff.png)
- Los picos de difracción de 8 puntas de las imágenes de estrellas del telescopio espacial James Webb se deben a la difracción causada por la forma hexagonal de las secciones del espejo y los puntales que sostienen el espejo secundario. [3]
- Utilizado como parol o estrella para el ID de la estación navideña ABS-CBN de 2010, Ngayong Pasko Magniningning Ang Pilipino ( literalmente , ' Esta Navidad, los filipinos brillarán ' ) debido al uso de un sol de la bandera filipina , lo que lo convierte también en un nacionalismo. y una canción con temática de patriotismo además de ser una canción navideña.
Véase también
- Uso
- Rub el Hizb – Personaje islámico
- Estrella selyúcida
- Shamsa
- Estrella de Ishtar : símbolo de la antigua diosa sumeria Inanna y su contraparte semítica oriental Ishtar y Venus romana .
- Seshat : el jeroglífico de esta antigua diosa egipcia representa una flor de siete pétalos, formando un octagrama con su tallo.
- Estrella de Lakshmi – Personaje indio
- Surya Majapahit : se utilizaba durante la época de Majapahit en Indonesia para representar a los dioses hindúes de las direcciones.
- Rosa de los vientos : se utiliza en brújulas para representar los puntos cardinales de los ocho vientos principales
- Auseklis – uso del octagrama regular por los letones
- Guñelve – representación de Venus en la iconografía mapuche .
- Selburose : uso del octagrama regular en el diseño noruego
- Utu – antiguo símbolo del dios mesopotámico y símbolo del dios Sol
- Las estrellas en general
- Otros
Referencias
- ^ γραμμή, Henry George Liddell, Robert Scott, Un léxico griego-inglés , sobre Perseo
- ^ El lado más luminoso de las matemáticas: Actas de la Conferencia en memoria de Eugène Strens sobre matemáticas recreativas y su historia (1994), Metamorfosis de polígonos , Branko Grünbaum
- ^ Lawrence, Pete (13 de septiembre de 2022). "¿Por qué todas las estrellas tienen 8 puntas en las imágenes de James Webb? Un astrónomo lo explica". BBC Science Focus Magazine . Consultado el 1 de marzo de 2023 .
- Grünbaum, B. y GC Shephard; Azulejos y patrones , Nueva York: WH Freeman & Co., (1987), ISBN 0-7167-1193-1 .
- Grünbaum, B. ; Poliedros con caras huecas, Actas de la Conferencia OTAN-ASI sobre politopos... etc. (Toronto 1993) , ed T. Bisztriczky et al., Kluwer Academic (1994) págs. 43–70.
- John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Capítulo 26, págs. 404: Politopos estelares regulares, dimensión 2)
Enlaces externos
- Weisstein, Eric W. "Octagrama". MathWorld .
