Geometría molecular octaédrica
| Geometría molecular octaédrica | |
|---|---|
 | |
| Ejemplos | SF6 , Mo(CO ) 6 |
| Grupo de puntos | Oh |
| Número de coordinación | 6 |
| Ángulo(s) de enlace | 90° |
| μ (Polaridad) | 0 |
En química , la geometría molecular octaédrica , también llamada bipiramidal cuadrada , [1] describe la forma de compuestos con seis átomos o grupos de átomos o ligandos dispuestos simétricamente alrededor de un átomo central, definiendo los vértices de un octaedro . El octaedro tiene ocho caras, de ahí el prefijo octa . El octaedro es uno de los sólidos platónicos , aunque las moléculas octaédricas suelen tener un átomo en su centro y no hay enlaces entre los átomos de los ligandos. Un octaedro perfecto pertenece al grupo puntual O h . Ejemplos de compuestos octaédricos son el hexafluoruro de azufre SF 6 y el hexacarbonilo de molibdeno Mo(CO) 6 . Los químicos utilizan el término "octaédrico" de forma algo vaga, centrándose en la geometría de los enlaces al átomo central y sin considerar las diferencias entre los propios ligandos. Por ejemplo, [Co(NH 3 ) 6 ] 3+ , que no es octaédrico en el sentido matemático debido a la orientación de los enlaces N−H , se denomina octaédrico. [2]
El concepto de geometría de coordinación octaédrica fue desarrollado por Alfred Werner para explicar las estequiometrías y la isomería en los compuestos de coordinación . Su descubrimiento permitió a los químicos racionalizar el número de isómeros de los compuestos de coordinación. Los complejos octaédricos de metales de transición que contienen aminas y aniones simples se denominan a menudo complejos de tipo Werner .

Isomería en complejos octaédricos
Cuando dos o más tipos de ligandos (L a , L b , ...) están coordinados a un centro metálico octaédrico (M), el complejo puede existir como isómeros. El sistema de denominación de estos isómeros depende del número y la disposición de los diferentes ligandos.
cisytrans
Para MLun
4yoel segundo
2Existen dos isómeros. Estos isómeros de MLun
4yoel segundo
2son cis , si los ligandos L b son mutuamente adyacentes, y trans , si los grupos L b están situados a 180° entre sí. Fue el análisis de tales complejos lo que llevó a Alfred Werner a la postulación de los complejos octaédricos, ganadora del Premio Nobel en 1913.
- cis- [ CoCl2 ( NH3 ) 4 ] +
- trans- [ CoCl2 ( NH3 ) 4 ] +
Isómeros faciales y meridionales
Para MLun
3yoel segundo
3Son posibles dos isómeros: un isómero facial ( fac ) en el que cada conjunto de tres ligandos idénticos ocupa una cara del octaedro que rodea al átomo de metal, de modo que dos de estos tres ligandos son mutuamente cis, y un isómero meridional ( mer ) en el que cada conjunto de tres ligandos idénticos ocupa un plano que pasa a través del átomo de metal.
- factor -[ CoCl3 ( NH3 ) 3 ]
- mer- [ CoCl3 ( NH3 ) 3 ]
Isómeros Δ y Λ
Los complejos con tres ligandos bidentados o dos ligandos bidentados cis pueden existir como pares enantioméricos . A continuación se muestran algunos ejemplos.
- Λ- [Fe(ox) 3 ] 3−
- Δ- [Fe(ox) 3 ] 3−
- Δ - cis -[CoCl 2 (en) 2 ] +
Otro
Para MLun
2yoel segundo
2yoc2
En total son posibles cinco isómeros geométricos y seis estereoisómeros. [3]
- Un isómero en el que los tres pares de ligandos idénticos son trans
- Tres isómeros en los que un par de ligandos idénticos (L a o L b o L c ) es trans mientras que los otros dos pares de ligandos son mutuamente cis .
- Dos pares enantioméricos en los que los tres pares de ligandos idénticos son cis . Estos son equivalentes a los isómeros Δ y Λ mencionados anteriormente.
El número de isómeros posibles puede llegar a 30 para un complejo octaédrico con seis ligandos diferentes (en cambio, para un complejo tetraédrico con cuatro ligandos diferentes solo son posibles dos estereoisómeros). La siguiente tabla enumera todas las combinaciones posibles para ligandos monodentados:
| Fórmula | Número de isómeros | Número de pares enantioméricos |
|---|---|---|
| ML6 | 1 | 0 |
| Mlun 5Lb | 1 | 0 |
| Mlun 4yoel segundo 2 | 2 | 0 |
| Mlun 4LbLc | 2 | 0 |
| Mlun 3yoel segundo 3 | 2 | 0 |
| Mlun 3yoel segundo 2L c | 3 | 0 |
| Mlun 3LbLcLd | 5 | 1 |
| Mlun 2yoel segundo 2yoc2 | 6 | 1 |
| Mlun 2yoel segundo 2LcLd | 8 | 2 |
| Mlun 2LbLcLdLe | 15 | 6 |
| ML a L b L c L d L e L f | 30 | 15 |
Por lo tanto, los 15 diastereómeros de ML a L b L c L d L e L f son quirales, mientras que para MLun
2L b L c L d L e , seis diastereómeros son quirales y tres no (aquellos en los que L a son trans ). Se puede ver que la coordinación octaédrica permite una complejidad mucho mayor que el tetraedro que domina la química orgánica . El tetraedro ML a L b L c L d existe como un único par enantiomérico. Para generar dos diastereómeros en un compuesto orgánico, se requieren al menos dos centros de carbono.
Desviaciones de la simetría ideal
Efecto Jahn-Teller
El término también puede referirse a octaédricos influenciados por el efecto Jahn-Teller , que es un fenómeno común en la química de coordinación . Esto reduce la simetría de la molécula de O h a D 4h y se conoce como distorsión tetragonal.
Geometría octaédrica distorsionada
Algunas moléculas, como XeF 6 o IF−
6, tienen un par solitario que distorsiona la simetría de la molécula de O h a C 3v . [4] [5] La geometría específica se conoce como octaedro monocapa , ya que se deriva del octaedro colocando el par solitario sobre el centro de una cara triangular del octaedro como una "capa" (y cambiando las posiciones de los otros seis átomos para acomodarlo). [6] Ambos representan una divergencia de la geometría predicha por VSEPR, que para AX 6 E 1 predice una forma piramidal pentagonal .
Estructuras bioctaédricas
Los pares de octaedros se pueden fusionar de una manera que preserve la geometría de coordinación octaédrica al reemplazar los ligandos terminales con ligandos puente . Dos motivos para la fusión de octaedros son comunes: compartir aristas y compartir caras. Los bioctaedros con aristas y caras compartidas tienen las fórmulas [M 2 L 8 (μ-L)] 2 y M 2 L 6 (μ-L) 3 , respectivamente. Las versiones poliméricas del mismo patrón de enlace dan las estequiometrías [ML 2 (μ-L) 2 ] ∞ y [M(μ-L) 3 ] ∞ , respectivamente.
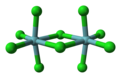
El hecho de compartir una arista o una cara de un octaedro da lugar a una estructura denominada bioctaédrica. Muchos compuestos de pentahaluro y pentaalcóxido metálicos existen en solución y en el sólido con estructuras bioctaédricas. Un ejemplo es el pentacloruro de niobio . Los tetrahaluros metálicos suelen existir como polímeros con octaedros que comparten aristas. El tetracloruro de circonio es un ejemplo. [7] Los compuestos con cadenas octaédricas que comparten caras incluyen MoBr 3 , RuBr 3 y TlBr 3 .
- Modelo de bolas y palos de pentacloruro de niobio , un compuesto de coordinación bioctaédrica.
- Modelo de bolas y palos de tetracloruro de circonio , un polímero inorgánico basado en octaedros que comparten aristas.
- Modelo de bolas y barras de bromuro de molibdeno (III) , un polímero inorgánico basado en octaedros que comparten caras.
- Vista casi a lo largo de la cadena de yoduro de titanio (III) que resalta el eclipse de los ligandos de haluro en dichos octaedros que comparten caras.
Geometría prismática trigonal
Para los compuestos con la fórmula MX 6 , la principal alternativa a la geometría octaédrica es una geometría prismática trigonal, que tiene simetría D 3h . En esta geometría, los seis ligandos también son equivalentes. También hay prismas trigonales distorsionados, con simetría C 3v ; un ejemplo destacado es W(CH 3 ) 6 . Se propone que la interconversión de los complejos Δ y Λ , que suele ser lenta, se realice a través de un intermedio prismático trigonal, un proceso llamado " giro de Bailar ". Una vía alternativa para la racemización de estos mismos complejos es el giro de Ray-Dutt .
Desdoblamiento de las energías de los orbitales d
Para un ion libre, p. ej. Ni 2+ o Mo 0 gaseosos , la energía de los orbitales d es igual en energía; es decir, están "degenerados". En un complejo octaédrico, esta degeneración se elimina. La energía de d z 2 y d x 2 − y 2 , el llamado conjunto e g , que están dirigidos directamente a los ligandos se desestabilizan. Por otro lado, la energía de los orbitales d xz , d xy y d yz , el llamado conjunto t 2g , se estabiliza. Las etiquetas t 2g y e g se refieren a representaciones irreducibles , que describen las propiedades de simetría de estos orbitales. La brecha de energía que separa estos dos conjuntos es la base de la teoría del campo cristalino y la teoría del campo de ligando más completa . La pérdida de degeneración tras la formación de un complejo octaédrico a partir de un ion libre se denomina división del campo cristalino o división del campo de ligando . La brecha de energía se denomina Δ o , que varía según el número y la naturaleza de los ligandos. Si la simetría del complejo es inferior a la octaédrica, los niveles e g y t 2g pueden dividirse aún más. Por ejemplo, los conjuntos t 2g y e g se dividen aún más en trans -MLun
4yoel segundo
2.
La fuerza del ligando tiene el siguiente orden para estos donadores de electrones:
Los llamados "ligandos de campo débil" dan lugar a Δ o pequeños y absorben luz en longitudes de onda más largas .
Reacciones
Dado que existe una variedad prácticamente incontable de complejos octaédricos, no es sorprendente que se hayan descrito una amplia variedad de reacciones. Estas reacciones pueden clasificarse de la siguiente manera:
- Reacciones de sustitución de ligandos (a través de una variedad de mecanismos)
- Reacciones de adición de ligandos, entre las que se incluyen muchas, la protonación.
- Reacciones redox (donde se ganan o pierden electrones)
- Reordenamientos en los que la estereoquímica relativa del ligando cambia dentro de la esfera de coordinación .
Muchas reacciones de complejos de metales de transición octaédricos ocurren en agua. Cuando un ligando aniónico reemplaza una molécula de agua coordinada, la reacción se llama anación . La reacción inversa, cuando el agua reemplaza un ligando aniónico, se llama acuación . Por ejemplo, el [CoCl(NH 3 ) 5 ] 2+ produce lentamente [Co(NH 3 ) 5 (H 2 O)] 3+ en agua, especialmente en presencia de ácido o base. La adición de HCl concentrado convierte el complejo acuoso nuevamente en cloruro, a través de un proceso de anación.
Véase también
Referencias
- ^ "Forma molecular bipiramidal trigonal @ Diccionario y glosario de química". glossary.periodni.com . Consultado el 3 de julio de 2022 .
- ^ Von Zelewsky, A. (1995). Estereoquímica de compuestos de coordinación . Chichester: John Wiley. ISBN 0-471-95599-X.
- ^ Miessler, GL; Tarr, DA (1999). Química inorgánica (2.ª ed.). Prentice-Hall. pág. 290. ISBN 0-13-841891-8.
- ^ Crawford, T. Daniel; Springer, Kristen W.; Schaefer, Henry F. (1994). "Una contribución a la comprensión de la estructura del hexafluoruro de xenón". Journal of Chemical Physics . 102 (8): 3307–3311. Código Bibliográfico :1995JChPh.102.3307C. doi :10.1063/1.468642.
- ^ Mahjoub, Ali R.; Seppelt, Konrad (1991). "La estructura de IF−
6". Edición internacional Angewandte Chemie . 30 (3): 323–324. doi :10.1002/anie.199103231. - ^ Winter, Mark (2015). "VSEPR y más de seis pares de electrones". Universidad de Sheffield: Departamento de Química . Consultado el 25 de septiembre de 2018.
La estructura de XeF
6
se basa en un octaedro distorsionado, probablemente hacia un octaedro monocapado.
- ^ Wells, AF (1984). Química inorgánica estructural . Oxford: Clarendon Press. ISBN 0-19-855370-6.
Enlaces externos
- Ejemplo de geometría octaédrica en 3dCHEM.com
- Centro de Estructura Molecular de la Universidad de Indiana
- Ejemplos de simetría de grupos de puntos
![cis-[CoCl2(NH3)4]+](http://upload.wikimedia.org/wikipedia/commons/thumb/b/be/Cis-dichlorotetraamminecobalt%28III%29.png/120px-Cis-dichlorotetraamminecobalt%28III%29.png)
![trans-[CoCl2(NH3)4]+](http://upload.wikimedia.org/wikipedia/commons/thumb/5/56/Trans-dichlorotetraamminecobalt%28III%29.png/120px-Trans-dichlorotetraamminecobalt%28III%29.png)
![factor-[CoCl3(NH3)3]](http://upload.wikimedia.org/wikipedia/commons/thumb/6/69/Fac-trichlorotriamminecobalt%28III%29.png/109px-Fac-trichlorotriamminecobalt%28III%29.png)
![mer-[CoCl3(NH3)3]](http://upload.wikimedia.org/wikipedia/commons/thumb/5/54/Mer-trichlorotriamminecobalt%28III%29.png/120px-Mer-trichlorotriamminecobalt%28III%29.png)
![Λ-[Fe(ox)3]3−](http://upload.wikimedia.org/wikipedia/commons/thumb/d/df/Delta-tris%28oxalato%29ferrate%28III%29-3D-balls.png/110px-Delta-tris%28oxalato%29ferrate%28III%29-3D-balls.png)
![Δ-[Fe(ox)3]3−](http://upload.wikimedia.org/wikipedia/commons/thumb/6/6e/Lambda-tris%28oxalato%29ferrate%28III%29-3D-balls.png/111px-Lambda-tris%28oxalato%29ferrate%28III%29-3D-balls.png)
![Λ-cis-[CoCl2(en)2]+](http://upload.wikimedia.org/wikipedia/commons/thumb/1/12/Delta-cis-dichlorobis%28ethylenediamine%29cobalt%28III%29.png/78px-Delta-cis-dichlorobis%28ethylenediamine%29cobalt%28III%29.png)
![Δ-cis-[CoCl2(en)2]+](http://upload.wikimedia.org/wikipedia/commons/thumb/8/81/Lambda-cis-dichlorobis%28ethylenediamine%29cobalt%28III%29.png/78px-Lambda-cis-dichlorobis%28ethylenediamine%29cobalt%28III%29.png)