Valor real y nominal

Parte de una serie sobre
Ciencias económicas
Historia Describir Índice
Ramas y clasificaciones Aplicado Econometría Heterodoxo Internacional Micro / Macro Corriente principal Matemático Methodology Political JEL classification codes
Concepts, theory and techniques Economic systems Economic growth Market National accounting Experimental economics Computational economics Game theory Operations research Middle income trap Industrial complex
By application Agricultural Behavioral Business Cultural Democracy Demographic Development Digitization Ecological Education Engineering Environmental Evolutionary Expeditionary Feminist Financial Geographical Happiness Health Historical Humanistic Industrial organization Information Institutional Knowledge Labour Law Managerial Monetary Natural resource Organizational Participation Personnel Planning Policy Public Public choice / Social choice theory Regional Rural Service Socio Sociological Solidarity Statistics Urban Welfare
Notable economists de Mandeville Quesnay Smith Malthus Say Ricardo von Thünen List Bastiat Cournot Mill Gossen Marx Walras Jevons George Menger Marshall Edgeworth Clark Pareto von Böhm-Bawerk von Wieser Veblen Fisher Pigou Heckscher von Mises Schumpeter Keynes Knight Polanyi Frisch Sraffa Myrdal Hayek Kalecki Röpke Kuznets Tinbergen Robinson von Neumann Hicks Lange Leontief Galbraith Koopmans Schumacher Friedman Samuelson Simon Buchanan Arrow Baumol Solow Rothbard Greenspan Sowell Becker Ostrom Sen Lucas Stiglitz Thaler Hoppe Krugman Piketty more
Lists Glossary Economists Publications (journals) Schools
Business portal Money portal
v t e

En economía , el valor nominal se refiere al valor medido en términos de cantidades absolutas de dinero , mientras que el valor real se considera y se mide en relación con los bienes o servicios reales por los que se puede intercambiar en un momento determinado. El valor real tiene en cuenta la inflación y el valor de un activo en relación con su poder adquisitivo .

En macroeconomía, el producto interno bruto real compensa la inflación, de modo que los economistas pueden excluir la inflación de las cifras de crecimiento y ver cuánto crece realmente una economía. El PIB nominal incluiría la inflación y, por lo tanto, sería más alto.

Un paquete de productos es una muestra de bienes que se utiliza para representar la suma total de bienes en toda la economía a la que pertenecen los bienes, con el propósito de realizar comparaciones en diferentes momentos (o lugares).

En un momento dado, un paquete de productos consiste en una lista de bienes, y cada bien de la lista tiene un precio de mercado y una cantidad. El valor de mercado del bien es el precio de mercado multiplicado por la cantidad en ese momento. El valor nominal del paquete de productos en un momento dado es el valor de mercado total del paquete de productos, que depende del precio de mercado y de la cantidad de cada bien del paquete de productos vigentes en ese momento.

Un índice de precios es el precio relativo de un conjunto de productos básicos. Un índice de precios puede medirse a lo largo del tiempo o en diferentes lugares o mercados. Si se mide a lo largo del tiempo, es una serie de valores a lo largo del tiempo . ${\displaystyle P_{t}}$${\displaystyle t}$

Un índice de precios de series temporales se calcula en relación con una fecha base o de referencia . es el valor del índice en la fecha base. Por ejemplo, si la fecha base es (finales de) 1992, es el valor del índice en (finales de) 1992. El índice de precios normalmente se normaliza para comenzar en 100 en la fecha base, por lo que se establece en 100.${\displaystyle P_{0}}$${\displaystyle P_{0}}$${\displaystyle P_{0}}$

El tiempo transcurrido entre cada valor de y el siguiente, normalmente es un intervalo de tiempo regular constante, como un año calendario. es el valor del índice de precios en el tiempo posterior a la fecha base. es igual a 100 veces el valor del paquete de productos en el tiempo , dividido por el valor del paquete de productos en la fecha base.${\displaystyle t}$${\displaystyle P_{t}}$${\displaystyle t}$${\displaystyle P_{t}}$${\displaystyle t}$

Si el precio del paquete de productos ha aumentado un uno por ciento durante el primer período después de la fecha base, entonces P ₁ = 101.

La tasa de inflación entre un momento y otro es el cambio en el índice de precios dividido por el valor del índice de precios en el momento :${\displaystyle i_{t}}$${\displaystyle t-1}$${\displaystyle t}$${\displaystyle t-1}$

${\displaystyle i_{t}={\frac {P_{t}-P_{t-1}}{P_{t-1}}}}$

${\displaystyle ={\frac {P_{t}}{P_{t-1}}}-1}$

expresado como porcentaje.

El valor nominal de un conjunto de productos tiende a cambiar con el tiempo. En cambio, por definición, el valor real del conjunto de productos permanece invariable a lo largo del tiempo. Los valores reales de los bienes o productos individuales pueden aumentar o disminuir entre sí, en términos relativos, pero un conjunto representativo de productos en su conjunto mantiene su valor real como constante de un período a otro.

Los valores reales pueden expresarse, por ejemplo, en dólares constantes de 1992 , con el nivel de precios fijado en 100 en la fecha base.

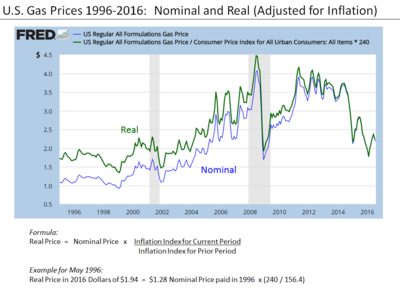
El índice de precios se aplica para ajustar el valor nominal de una cantidad, como los salarios o la producción total, para obtener su valor real. El valor real es el valor expresado en términos de poder adquisitivo en el año base.${\displaystyle Q}$

El precio del índice dividido por su valor del año base da el factor de crecimiento del índice de precios.${\displaystyle P_{t}/P_{0}}$

Los valores reales se pueden hallar dividiendo el valor nominal por el factor de crecimiento de un índice de precios. Si se utiliza el factor de crecimiento del índice de precios como divisor para convertir un valor nominal en un valor real, el valor real en el momento t en relación con la fecha base es:

${\displaystyle {\frac {P_{0}\cdot Q_{t}}{P_{t}}}}$

La tasa de crecimiento real es el cambio en una cantidad nominal en términos reales desde la fecha anterior . Mide cuánto ha cambiado el poder adquisitivo de la cantidad a lo largo de un período único.${\displaystyle r_{t}}$${\displaystyle Q_{t}}$${\displaystyle t-1}$

${\displaystyle r_{t}={\frac {P_{0}\cdot Q_{t}}{P_{t}}}{\Bigg /}{\frac {P_{0}\cdot Q_{t-1}}{P_{t-1}}}-1}$

${\displaystyle ={\frac {P_{t-1}\cdot Q_{t}}{P_{t}\cdot Q_{t-1}}}-1}$

${\displaystyle ={\frac {Q_{t}}{Q_{t-1}}}({\frac {P_{t}}{P_{t-1}}})^{-1}-1}$

${\displaystyle ={\frac {1+g_{t}}{1+i_{t}}}-1}$

donde es la tasa de crecimiento nominal de , y es la tasa de inflación.${\displaystyle g_{t}}$${\displaystyle Q_{t}}$${\displaystyle i_{t}}$

${\displaystyle 1+r_{t}={\frac {1+g_{t}}{1+i_{t}}}}$

Para valores entre −1 y 1 (es decir, ±100 por ciento), tenemos la serie de Taylor${\displaystyle i_{t}}$

${\displaystyle (1+i_{t})^{-1}=1-i_{t}+i_{t}^{2}-i_{t}^{3}+...}$

entonces

${\displaystyle 1+r_{t}=(1+g_{t})(1-i_{t}+i_{t}^{2}-i_{t}^{3}+...)}$

${\displaystyle =1+g_{t}-i_{t}-g_{t}i_{t}+i_{t}^{2}+{\text{higher order terms.}}}$

Por lo tanto, como aproximación de primer orden ( es decir , lineal),

${\displaystyle r_{t}=g_{t}-i_{t}}$

El conjunto de bienes que se utiliza para medir el índice de precios al consumidor (IPC) es aplicable a los consumidores. Por lo tanto, para los asalariados en su calidad de consumidores, una forma adecuada de medir los salarios reales (el poder adquisitivo de los salarios) es dividir el salario nominal (después de impuestos) por el factor de crecimiento del IPC.

El producto interno bruto (PIB) es una medida de la producción agregada. El PIB nominal en un período determinado refleja los precios vigentes en ese momento, mientras que el PIB real compensa la inflación. Los índices de precios y las Cuentas Nacionales de Ingresos y Productos de Estados Unidos se construyen a partir de paquetes de productos básicos y sus respectivos precios. En el caso del PIB, un índice de precios adecuado es el índice de precios del PIB. En las Cuentas Nacionales de Ingresos y Productos de Estados Unidos, el PIB nominal se denomina PIB en dólares corrientes (es decir, en precios vigentes para cada año designado), y el PIB real se denomina PIB en dólares [del año base] (es decir, en dólares que pueden comprar la misma cantidad de productos básicos que en el año base).

Como se mostró en la sección anterior sobre la tasa de crecimiento real,

${\displaystyle 1+r_{t}={\frac {1+g_{t}}{1+i_{t}}}}$

dónde

${\displaystyle r_{t}}$es la tasa de aumento de una cantidad en términos reales,

${\displaystyle g_{t}}$es la tasa de aumento de la misma cantidad en términos nominales, y

${\displaystyle i_{t}}$es la tasa de inflación,

y como aproximación de primer orden,

${\displaystyle r_{t}=g_{t}-i_{t}.}$

En el caso en que la cantidad creciente sea un activo financiero , sea una tasa de interés nominal y sea la tasa de interés real correspondiente , la aproximación de primer orden se conoce como ecuación de Fisher . ^[1]${\displaystyle g_{t}}$${\displaystyle r_{t}}$${\displaystyle r_{t}=g_{t}-i_{t}}$

Si nos remontamos al pasado, la tasa de interés real ex post es aproximadamente la tasa de interés nominal histórica menos la inflación. Si nos adentramos en el futuro, la tasa de interés real esperada es aproximadamente la tasa de interés nominal menos la tasa de inflación esperada.

No sólo los datos de series temporales , como los mencionados anteriormente, sino también los datos transversales que dependen de precios que pueden variar geográficamente, por ejemplo, se pueden ajustar de manera similar. Por ejemplo, el valor total de un bien producido en una región de un país depende tanto de la cantidad como del precio. Para comparar la producción de diferentes regiones, la producción nominal de una región se puede ajustar modificando el precio de los bienes a precios comunes o promedio.

• Diewert, WE (2008) [1987]. "Números índice". Diccionario de economía New Palgrave (2.ª ed.). págs. 1–32. doi :10.1057/978-1-349-95121-5_940-2. ISBN 978-1-349-95121-5.
• O'Donnell, R. (1987). "Cantidades reales y nominales". The New Palgrave: A Dictionary of Economics . Vol. v. 4. págs. 97–98.( La distinción temprana de Adam Smith reivindicada)
• Sen, Amartya (1979). "La base del bienestar en las comparaciones de ingresos reales: una encuesta". Revista de literatura económica . 17 (1): 1–45. JSTOR  2723639.
• Usher, D. (1987). "Ingreso real". The New Palgrave: A Dictionary of Economics . Vol. v. 4. págs. 104–05.

• Conceptos básicos de datos: conversión de los valores nominales en valores reales según el Banco de la Reserva Federal de Dallas
• Calculadora de inflación del IPC de la Oficina de Estadísticas Laborales de EE. UU.