Kelvin
Unidad de temperatura del SI

Kelvin
Temperaturas equivalentes en kelvin (K), Celsius (°C) y Fahrenheit  (°F)
información general
Sistema de unidadesSI
Unidad detemperatura
SímboloK
Llamado en honor aWilliam Thomson, primer barón Kelvin
Definición de 2019kB ≝​1.380 649 × 10 −23 ⁠Yo/K⁠
Conversiones
x  K en ...... corresponde a...
   Celsius   ( x  − 273,15) °C
   Fahrenheit   (1,8  x  − 459,67) °F
   Rango   1,8  x  °Ra

El kelvin (símbolo: K ) es la unidad base de temperatura en el Sistema Internacional de Unidades (SI). La escala Kelvin es una escala de temperatura absoluta que comienza en la temperatura más baja posible ( cero absoluto ), que se toma como 0 K. [1] [2] [3] [4] Por definición, la escala Celsius (símbolo °C) y la escala Kelvin tienen exactamente la misma magnitud; es decir, un aumento de 1 K es igual a un aumento de 1 °C y viceversa, y cualquier temperatura en grados Celsius se puede convertir a kelvin sumando 273,15. [1] [5]

El científico británico del siglo XIX Lord Kelvin fue el primero en desarrollar y proponer la escala. [5] A principios del siglo XX, a menudo se la denominaba escala "Celsius absoluta". [6] El kelvin se agregó formalmente al Sistema Internacional de Unidades en 1954, definiendo 273,16 K como el punto triple del agua . Las escalas Celsius, Fahrenheit y Rankine se redefinieron en términos de la escala Kelvin utilizando esta definición. [2] [7] [8] La revisión de 2019 del SI ahora define el kelvin en términos de energía al establecer la constante de Boltzmann exactamente en 1.380 649 × 10 −23  julios por kelvin; [2] cada cambio de 1 K en la temperatura termodinámica corresponde a un cambio de energía térmica de exactamente1,380 649 × 10 −23  J .

Historia

Precursores

Un baño de agua helada ofrecía un punto de calibración práctico para los termómetros (mostrados aquí en Celsius) antes de que se comprendiera bien la naturaleza física del calor.

Durante el siglo XVIII se desarrollaron múltiples escalas de temperatura , [9] en particular Fahrenheit y centígrados (más tarde Celsius). Estas escalas precedieron a gran parte de la ciencia moderna de la termodinámica , incluida la teoría atómica y la teoría cinética de los gases que sustentan el concepto de cero absoluto. En cambio, eligieron puntos definitorios dentro del rango de la experiencia humana que se podían reproducir fácilmente y con una precisión razonable, pero que carecían de un significado profundo en la física térmica. En el caso de la escala Celsius (y las escalas Newton y Réaumur , que ya no existen desde hace mucho tiempo ), el punto de fusión del hielo sirvió como punto de partida, y Celsius se definió (desde la década de 1740 hasta la de 1940 ) calibrando un termómetro de manera que:

Esta definición supone agua pura a una presión específica elegida para aproximarse a la presión natural del aire al nivel del mar. Por lo tanto, un incremento de 1 °C equivale a ⁠1/100⁠ de la diferencia de temperatura entre los puntos de fusión y ebullición. El mismo intervalo de temperatura se utilizó posteriormente para la escala Kelvin.

Ley de Charles

Entre 1787 y 1802, Jacques Charles (inédito), John Dalton [10] [ 11] y Joseph Louis Gay-Lussac [12] determinaron que, a presión constante, los gases ideales expandían o contraían su volumen linealmente ( ley de Charles ) en aproximadamente 1/273 partes por grado Celsius de cambio de temperatura hacia arriba o hacia abajo, entre 0 °C y 100 °C. La extrapolación de esta ley sugirió que un gas enfriado a aproximadamente -273 °C ocuparía un volumen cero.

Señor Kelvin

Lord Kelvin , el homónimo de la unidad de medida.

Primera escala absoluta

En 1848, William Thomson, quien más tarde fue ennoblecido como Lord Kelvin , publicó un artículo titulado On an Absolute Thermometric Scale (Sobre una escala termométrica absoluta ) . [13] La escala propuesta en el artículo resultó ser insatisfactoria, pero los principios y fórmulas en los que se basaba la escala eran correctos. [14] Por ejemplo, en una nota al pie, Thomson derivó el valor de −273 °C para el cero absoluto calculando el recíproco negativo de 0,00366 (el coeficiente de expansión térmica de un gas ideal por grado Celsius en relación con el punto de hielo). [15] Este valor derivado concuerda con el valor actualmente aceptado de −273,15 °C, lo que permite la precisión e incertidumbre involucradas en el cálculo.

La escala fue diseñada sobre el principio de que "una unidad de calor que desciende de un cuerpo A a la temperatura T ° de esta escala, a un cuerpo B a la temperatura ( T − 1)° , produciría el mismo efecto mecánico, cualquiera que sea el número T ." [16] Específicamente, Thomson expresó la cantidad de trabajo necesario para producir una unidad de calor (la eficiencia térmica ) como , donde es la temperatura en Celsius, es el coeficiente de expansión térmica, y era la "función de Carnot", una cantidad independiente de la sustancia que depende de la temperatura, [17] motivada por una versión obsoleta del teorema de Carnot . [14] [18] La escala se deriva al encontrar un cambio de variables de temperatura tal que sea proporcional a . micras ( a ) ( 1 + mi a ) / mi {\displaystyle \mu (t)(1+Et)/E} a {\estilo de visualización t} mi {\estilo de visualización E} micras ( a ) {\displaystyle \mu(t)} yo 1848 = F ( yo ) Estilo de visualización T_{1848}=f(T)} yo {\estilo de visualización T} d yo 1848 / d yo Estilo de visualización: dT_{1848}/dT micras {\estilo de visualización \mu}

Termómetro que muestra la temperatura en kelvin y grados Celsius

Cuando Thomson publicó su artículo en 1848, solo consideró las mediciones experimentales de Regnault de . [19] Ese mismo año, James Prescott Joule le sugirió a Thomson que la verdadera fórmula para la función de Carnot era [20] donde es "el equivalente mecánico de una unidad de calor", [21] ahora conocida como la capacidad calorífica específica del agua, aproximadamente 771,8 libras-pie fuerza por grado Fahrenheit por libra (4153 J/K/kg). [22] Thomson inicialmente se mostró escéptico sobre las desviaciones de la fórmula de Joule con respecto al experimento, afirmando "Creo que se admitirá generalmente que no puede haber tal inexactitud en la parte de los datos de Regnault, y solo queda la incertidumbre con respecto a la densidad del vapor saturado". [23] Thomson se refirió a la exactitud de la fórmula de Joule como " la hipótesis de Mayer ", debido a que Mayer la había asumido por primera vez. [24] Thomson organizó numerosos experimentos en coordinación con Joule, concluyendo finalmente en 1854 que la fórmula de Joule era correcta y que el efecto de la temperatura en la densidad del vapor saturado explicaba todas las discrepancias con los datos de Regnault. [25] Por lo tanto, en términos de la escala Kelvin moderna , la primera escala podría expresarse de la siguiente manera: [18] Los parámetros de la escala se eligieron arbitrariamente para que coincidieran con la escala Celsius a 0° y 100 °C o 273 y 373 K (los puntos de fusión y ebullición del agua). [26] En esta escala, un aumento de aproximadamente 222 grados corresponde a una duplicación de la temperatura Kelvin, independientemente de la temperatura inicial, y el "frío infinito" ( cero absoluto ) tiene un valor numérico de infinito negativo . [27] micras ( a ) {\displaystyle \mu(t)} micras ( a ) = Yo mi 1 + mi a , {\displaystyle \mu (t)=J{\frac {E}{1+Et}},} Yo {\displaystyle J} T {\displaystyle T} T 1848 = 100 × log ⁡ ( T / 273 K ) log ⁡ ( 373 K / 273 K ) {\displaystyle T_{1848}=100\times {\frac {\log(T/{\text{273 K}})}{\log({\text{373 K}}/{\text{273 K}})}}}

Escala absoluta moderna

Thomson comprendió que con la fórmula propuesta por Joule para , la relación entre el trabajo y el calor para un motor termodinámico perfecto era simplemente la constante . [28] En 1854, Thomson y Joule formularon una segunda escala absoluta que era más práctica y conveniente, y que coincidía con los termómetros de aire para la mayoría de los propósitos. [29] Específicamente, "la medida numérica de la temperatura será simplemente el equivalente mecánico de la unidad térmica dividida por la función de Carnot". [30] μ {\displaystyle \mu } J {\displaystyle J}

Para explicar esta definición, considere un motor de ciclo de Carnot reversible, donde es la cantidad de energía térmica transferida al sistema, es el calor que sale del sistema, es el trabajo realizado por el sistema ( ), es la temperatura del depósito caliente en Celsius, y es la temperatura del depósito frío en Celsius. La función de Carnot se define como , y la temperatura absoluta como . Se encuentra la relación . Al suponer , se obtiene el principio general de una escala de temperatura termodinámica absoluta para el motor de Carnot, . Se puede demostrar que la definición corresponde a la temperatura termométrica de las leyes de los gases ideales . [31] Q H {\displaystyle Q_{H}} Q C {\displaystyle Q_{C}} W {\displaystyle W} Q H − Q C {\displaystyle Q_{H}-Q_{C}} t H {\displaystyle t_{H}} t C {\displaystyle t_{C}} μ = W / Q H / ( t H − t C ) {\displaystyle \mu =W/Q_{H}/(t_{H}-t_{C})} T H = J / μ {\displaystyle T_{H}=J/\mu } T H = J × Q H × ( t H − t C ) / W {\displaystyle T_{H}=J\times Q_{H}\times (t_{H}-t_{C})/W} T H − T C = J × ( t H − t c ) {\displaystyle T_{H}-T_{C}=J\times (t_{H}-t_{c})} Q H / T H = Q C / T C {\displaystyle Q_{H}/T_{H}=Q_{C}/T_{C}}

Esta definición por sí sola no es suficiente. Thomson especificó que la escala debe tener dos propiedades: [32]

  • Los valores absolutos de dos temperaturas son entre sí la proporción del calor absorbido al calor rechazado en un motor termodinámico perfecto que funciona con una fuente y un refrigerador a la temperatura más alta y más baja respectivamente.
  • La diferencia de temperatura entre los puntos de congelación y ebullición del agua bajo presión atmosférica normal se denominará 100 grados (el mismo incremento que en la escala Celsius). Las mejores estimaciones de Thomson en ese momento eran que la temperatura del agua congelada era de 273,7 K y la temperatura del agua hirviendo era de 373,7 K. [33]

Estas dos propiedades se incluirían en todas las versiones futuras de la escala Kelvin, aunque todavía no se la conocía con ese nombre. En las primeras décadas del siglo XX, la escala Kelvin se denominaba a menudo escala " Celsius absoluta ", indicando los grados Celsius contados a partir del cero absoluto en lugar del punto de congelación del agua, y utilizando el mismo símbolo para los grados Celsius normales, °C. [6]

Estándar de triple punto

Diagrama de fases típico . La línea verde continua se aplica a la mayoría de las sustancias; la línea verde discontinua muestra el comportamiento anómalo del agua. La línea de ebullición (azul continua) va desde el punto triple hasta el punto crítico , más allá del cual, si se incrementa aún más la temperatura y la presión, se produce un fluido supercrítico .

En 1873, el hermano mayor de William Thomson, James , acuñó el término punto triple [34] para describir la combinación de temperatura y presión a la que las fases sólida, líquida y gaseosa de una sustancia eran capaces de coexistir en equilibrio termodinámico . Si bien dos fases cualesquiera podrían coexistir a lo largo de un rango de combinaciones de temperatura y presión (por ejemplo, el punto de ebullición del agua puede verse afectado de manera bastante drástica al aumentar o disminuir la presión), la condición de punto triple para una sustancia dada solo puede ocurrir a una sola presión y solo a una sola temperatura. En la década de 1940, se había medido experimentalmente que el punto triple del agua era aproximadamente el 0,6% de la presión atmosférica estándar y muy cerca de 0,01 °C según la definición histórica de Celsius que se usaba entonces.

En 1948, la escala Celsius fue recalibrada asignando a la temperatura del punto triple del agua el valor exacto de 0,01 °C [35] y permitiendo que el punto de fusión a presión atmosférica estándar tuviera un valor determinado empíricamente (y que el punto de fusión real a presión ambiental tuviera un valor fluctuante ) cercano a 0 °C. Esto se justificó con el argumento de que se consideró que el punto triple daba una temperatura de referencia reproducible con mayor precisión que el punto de fusión. [36] El punto triple podía medirse con una precisión de ±0,0001 °C, mientras que el punto de fusión solo con ±0,001 °C. [35]

En 1954, cuando se había determinado experimentalmente que el cero absoluto era aproximadamente -273,15 °C según la definición de °C que se utilizaba entonces, la Resolución 3 de la 10.ª Conferencia General de Pesas y Medidas (CGPM) introdujo una nueva escala Kelvin estandarizada internacionalmente que definía el punto triple exactamente como 273,15 + 0,01 = 273,16 grados Kelvin. [37] [38]

En 1967/1968, la Resolución 3 de la 13ª CGPM renombró la unidad de incremento de temperatura termodinámica "kelvin", símbolo K, reemplazando "grado Kelvin", símbolo °K. [39] [40] [41] La 13ª CGPM también sostuvo en la Resolución 4 que "El kelvin, unidad de temperatura termodinámica, es igual a la fracción1/273,16⁠ de la temperatura termodinámica del punto triple del agua." [4] [42] [43]

Después de la redefinición del metro en 1983 , el kelvin, el segundo y el kilogramo quedaron como las únicas unidades del SI no definidas con referencia a ninguna otra unidad.

En 2005, al observar que el punto triple podía verse influenciado por la relación isotópica del hidrógeno y el oxígeno que componen una muestra de agua y que esta era "ahora una de las principales fuentes de la variabilidad observada entre diferentes realizaciones del punto triple del agua", el Comité Internacional de Pesas y Medidas (CIPM), un comité de la CGPM, afirmó que para los fines de delinear la temperatura del punto triple del agua, la definición del kelvin se referiría al agua que tiene la composición isotópica especificada para el Agua Media del Océano Estándar de Viena . [4] [44] [45]

Redefinición de 2019

Dependencias de las unidades del SI de 2019. El kelvin (K) ahora está fijado en términos de la constante de Boltzmann ( k B ) y el julio . El julio no se muestra porque es una unidad derivada definida por el metro (m), el segundo (s) y el kilogramo (kg). Esas unidades básicas del SI están definidas por las constantes universales de la velocidad de la luz ( c ), la frecuencia de transición hiperfina del cesio-133 ( Δ ν Cs ) y la constante de Planck ( h ). Las flechas negras trazan las dependencias de estas constantes con el kelvin.

En 2005, el CIPM inició un programa para redefinir el kelvin (junto con otras unidades básicas del SI ) utilizando un método experimentalmente más riguroso. En particular, el comité propuso redefinir el kelvin de manera que la constante de Boltzmann ( k B ) tomara el valor exacto1.380 6505 × 10 −23  J/K . [46] El comité esperaba que el programa se completara a tiempo para su adopción por la CGPM en su reunión de 2011, pero en la reunión de 2011 la decisión se pospuso a la reunión de 2014 cuando se consideraría parte de un programa más amplio . [47] Un desafío fue evitar degradar la precisión de las mediciones cercanas al punto triple. La redefinición se pospuso nuevamente en 2014, a la espera de mediciones más precisas de la constante de Boltzmann en términos de la definición actual, [48] pero finalmente se adoptó en la 26.ª CGPM a fines de 2018, con un valor de k B  = 1.380 649 × 10 −23  J⋅K −1 . [49] [46] [1] [2] [4] [50]

Para fines científicos, la principal ventaja de la redefinición es que permite realizar mediciones más precisas a temperaturas muy bajas y muy altas, ya que las técnicas utilizadas dependen de la constante de Boltzmann. La independencia de cualquier sustancia o medición en particular también es una ventaja filosófica. El kelvin ahora solo depende de la constante de Boltzmann y de las constantes universales (ver el diagrama de dependencias de unidades del SI de 2019), lo que permite expresarlo exactamente como: [2]

1 kelvin = ⁠1.380 649 × 10 −23/(6.626 070 15 × 10 −34 )(9 192 631 770 )⁠ ⁠h Δ ν Cs/k B⁠ = ⁠13.806 49/6.091 102 297 113 866 55⁠ ⁠h Δ ν Cs/k B⁠ .

Para efectos prácticos, la redefinición pasó desapercibida; se utilizaron suficientes dígitos para la constante de Boltzmann para garantizar que 273,16 K tenga suficientes dígitos significativos para contener la incertidumbre del punto triple del agua [51] y que el agua todavía se congele normalmente a 0 °C [52] con un alto grado de precisión. Pero antes de la redefinición, el punto triple del agua era exacto y la constante de Boltzmann tenía un valor medido de1.380 649 03 (51) × 10 −23  J/K , con una incertidumbre estándar relativa de3,7 × 10 −7 . [51] Posteriormente, la constante de Boltzmann es exacta y la incertidumbre se transfiere al punto triple del agua, que ahora es273.1600(1) K. [ a]

La nueva definición entró oficialmente en vigor el 20 de mayo de 2019, el 144º aniversario de la Convención del Metro . [50] [1] [2] [4]

Usos prácticos

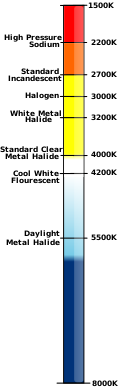
Temperatura de color (derecha) de varias fuentes de luz (izquierda)

Temperatura del color

El kelvin se utiliza a menudo como medida de la temperatura de color de las fuentes de luz. La temperatura de color se basa en el principio de que un radiador de cuerpo negro emite luz con una distribución de frecuencia característica de su temperatura. Los cuerpos negros a temperaturas inferiores a4000 K aparecen rojizos, mientras que los que están por encima de7500 K aparecen azulados. La temperatura de color es importante en los campos de proyección de imágenes y fotografía, donde una temperatura de color de aproximadamenteSe requieren 5600 K para que coincidan con las emulsiones de película de "luz diurna".

En astronomía , la clasificación estelar de las estrellas y su lugar en el diagrama de Hertzsprung-Russell se basan, en parte, en su temperatura superficial, conocida como temperatura efectiva . La fotosfera del Sol , por ejemplo, tiene una temperatura efectiva de5772 K [1][2][3][4] según lo adoptado por la Resolución B3 de la UAI de 2015.

Las cámaras digitales y el software fotográfico suelen utilizar la temperatura de color en K en los menús de edición y configuración. La sencilla regla es que una temperatura de color más alta produce una imagen con tonos blancos y azules más intensos. La reducción de la temperatura de color produce una imagen en la que predominan los colores rojizos y "más cálidos" .

Kelvin como unidad de temperatura de ruido

En electrónica , el kelvin se utiliza como indicador de lo ruidoso que es un circuito en relación con un nivel de ruido final , es decir, la temperatura de ruido . El ruido de Johnson-Nyquist de las resistencias (que produce un ruido kTC asociado cuando se combina con condensadores ) es un tipo de ruido térmico derivado de la constante de Boltzmann y se puede utilizar para determinar la temperatura de ruido de un circuito utilizando las fórmulas de Friis para el ruido .

Unidades derivadas y múltiplos del SI

La única unidad derivada del SI con un nombre especial derivado del kelvin es el grado Celsius. Al igual que otras unidades del SI, el kelvin también se puede modificar añadiéndole un prefijo métrico que lo multiplique por una potencia de 10 :

Múltiplos del kelvin (K) en el SI
SubmúltiplosMúltiplos
ValorSímbolo del SINombreValorSímbolo del SINombre
10 −1  Kesdecikelvin10 1  KDaKdecaquelvin
10 −2  KcKcentikelvin10 2  KHong Konghectokelvin
10 −3  KmKmilikelvin10 3  KkKkilokelvin
10 −6  KmicroKmicrokelvin10 6  KMKmegakelvin
10 −9  KNo soynanokelvin10 9  KG.K.gigakelvin
10 −12  Kpaquetepicokelvin10 12  KConocimiento tradicionalterakelvin
10 −15  Kpor favorfemtokelvin10 15  KPAQUETEpetakelvin
10 −18  KAlaskaattokelvin10 18  KEkexakelvin
10 −21  KzKzeptokelvin10 21  KZKceluloide
10 −24  KSí, sí.yoctokelvin10 24  KSí, síYottakelvin
10 −27  KrKrontokelvin10 27  KR.K.Ronna Kelvin
10 −30  KqKquectokelvin10 30  milQKQuettakelvin

Ortografía

Según la convención del SI, el kelvin nunca se menciona ni se escribe como un grado . La palabra "kelvin" no se escribe con mayúscula cuando se usa como unidad. Puede estar en forma plural según corresponda (por ejemplo, "hay 283 kelvins afuera", como para "hay 50 grados Fahrenheit" y "10 grados Celsius"). [54] [5] [55] [56] El símbolo de la unidad K es una letra mayúscula, [39] según la convención del SI para escribir con mayúscula los símbolos de unidades derivadas del nombre de una persona. [57] Es una convención común escribir Kelvin con mayúscula cuando se hace referencia a Lord Kelvin [5] o la escala Kelvin. [58]

El símbolo de unidad K está codificado en Unicode en el punto de código U+212A K SIGNO DE KELVIN . Sin embargo, este es un carácter de compatibilidad proporcionado para la compatibilidad con codificaciones heredadas. El estándar Unicode recomienda utilizar en su lugar U+004B K LETRA MAYÚSCULA LATINA K ; es decir, una K mayúscula normal . "Se ha dado equivalencia canónica a tres símbolos similares a letras con letras regulares: U+2126 Ω SIGNO DE OHMIO , U+212A K SIGNO DE KELVIN y U+212B Å SIGNO DE ANGSTROM . En los tres casos, se debe utilizar la letra regular". [59]

Véase también

Notas

  1. ^ La incertidumbre absoluta se puede calcular como 273,16 ×3,7 × 10 −7  K , que se puede redondear a0,10 mK para todos los efectos prácticos. [53]

Referencias

  1. ^ abcd BIPM (2019-05-20). "Mise en pratique for the definition of the kelvin in the SI" (Mise en pratique para la definición del kelvin en el SI). BIPM.org . Consultado el 18 de febrero de 2022 .
  2. ^ abcdef «Folleto SI: El Sistema Internacional de Unidades (SI) – Novena edición (actualizado en 2022)». BIPM . Consultado el 7 de septiembre de 2022 .
  3. ^ "Unidad básica del SI: kelvin (K)". BIPM . Consultado el 5 de marzo de 2022 .
  4. ^ abcde "Un punto de inflexión para la humanidad: redefinición del sistema de medición del mundo". NIST . 2018-05-12 . Consultado el 2022-02-21 .
  5. ^ abcd "Kelvin: Introducción". NIST . 2018-05-14 . Consultado el 2022-09-02 .
  6. ^ En las ediciones de la Enciclopedia Británica de los años 1920 y 1950, el artículo "Planetas".
  7. ^ Benham, Elizabeth (6 de octubre de 2020). "Derribando mitos sobre el sistema métrico". NIST . Taking Measure (blog oficial del NIST) . Consultado el 21 de febrero de 2022 .
  8. ^ "Manual 44 – 2022 – Apéndice C – Tablas generales de unidades de medida" (PDF) . nist.gov . NIST . Consultado el 21 de febrero de 2022 .
  9. ^ "Kelvin: Historia". NIST . 2018-05-14 . Consultado el 2022-02-21 .
  10. ^ Dalton, John (1801). "Ensayo II. Sobre la fuerza del vapor de agua y otros líquidos, tanto en vacío como en aire". Memorias de la Sociedad Literaria y Filosófica de Manchester . 5 parte 2: 550–574.
  11. ^ Dalton, John (1801). "Ensayo IV. Sobre la expansión de fluidos elásticos por el calor". Memorias de la Sociedad Literaria y Filosófica de Manchester . 5 parte 2: 595–602.
  12. ^ Gay-Lussac, Joseph Louis (1802), "Recherches sur la dilatation des gaz et des vapeurs", Annales de Chimie , XLIII : 137Traducción al español (extracto).
  13. ^ Thomson 1882, págs. 100–106.
  14. ^ ab Magie, William Francis (1935). Un libro de consulta sobre física. pág. 237.
  15. ^ Thomson 1882, p. 104: "Si llevamos suficientemente lejos el estricto principio de graduación, enunciado anteriormente, llegaríamos a un punto correspondiente al volumen de aire reducido a nada, que estaría marcado como −273° de la escala (−100/·366, si ·366 es el coeficiente de expansión); y por lo tanto −273° del termómetro de aire es un punto que no se puede alcanzar a ninguna temperatura finita, por baja que sea."
  16. ^ Thomson 1882, pág. 104.
  17. ^ Thomson 1882, pág. 187.
  18. ^ desde Thomson 1882, pág. 106.
  19. ^ Thomson 1882, pág. 193.
  20. ^ Thomson 1882, pág. 212.
  21. ^ Thomson 1882, pág. 186.
  22. ^ Thomson 1882, pág. 192.
  23. ^ Thomson 1882, págs. 214-215.
  24. ^ Thomson 1882, pág. 213.
  25. ^ Thomson 1882, pág. 388.
  26. ^ Thomson 1882, p. 105: "Los puntos arbitrarios que coinciden en las dos escalas son 0° y 100°"
  27. ^ Saslow, WM (7 de enero de 2020). "Una historia de la termodinámica: el manual que faltaba". Entropía . 22 (1). eqn. (36). Bibcode :2020Entrp..22...77S. doi : 10.3390/e22010077 . PMC 7516509 . PMID  33285852. 
  28. ^ Thomson 1882, pág. 190, fórmula (7).
  29. ^ Thomson 1882, págs. 106, 232–236.
  30. ^ Thomson 1882, pág. 234.
  31. ^ Wang, Lin-Shu (2020). Un tratado sobre calor y energía . Cham: Springer. pág. 77. ISBN 9783030057466.
  32. ^ Thomson 1882, pág. 235.
  33. ^ Thomson 1882, pág. 236.
  34. ^ Thomson, James (1873). "Una investigación cuantitativa de ciertas relaciones entre los estados gaseoso, líquido y sólido de la sustancia acuosa". Actas de la Royal Society de Londres . 22 : 28. Bibcode :1873RSPS...22...27T. ISSN  0370-1662. y, en consecuencia, que las tres curvas se encontrarían o se cruzarían en un punto, que he llamado el punto triple .
  35. ^ ab Swinton, FL (septiembre de 1967). "El punto triplete del agua". Revista de educación química . 44 (9): 541. Bibcode :1967JChEd..44..541S. doi :10.1021/ed044p541. ISSN  0021-9584.
  36. ^ "Resolución 3 de la 9ª CGPM (1948)". BIPM . Consultado el 21 de febrero de 2022 .
  37. ^ "Resolución 3 de la 10ª CGPM (1954)". BIPM . Consultado el 21 de febrero de 2022 .
  38. ^ "Resolución 3: Definición de la escala termodinámica de temperaturas". Resoluciones de la 10ª CGPM . Bureau International des Poids et Mesures. 1954. Archivado desde el original el 23 de junio de 2007. Consultado el 6 de febrero de 2008 .
  39. ^ ab "Resolución 3 de la 13ª CGPM (1967)". BIPM . Consultado el 21 de febrero de 2022 .
  40. ^ "Resolución 3: Unidad SI de temperatura termodinámica (kelvin)". Resoluciones de la 13.ª CGPM . Bureau International des Poids et Mesures. 1967. Archivado desde el original el 2007-04-21 . Consultado el 2008-02-06 .
  41. ^ Westphal, Wilhelm Heinrich (1952). "Nox, Dunkelleuchtdichte, Skot". En Westphal, Wilhelm H. (ed.). Physikalisches Wörterbuch (en alemán) (1 ed.). Berlín / Gotinga / Heidelberg, Alemania: Springer-Verlag OHG . págs.125, 271, 389. doi :10.1007/978-3-662-12706-3. ISBN 978-3-662-12707-0. Consultado el 16 de marzo de 2023 . págs.271, 389: Dunkelleuchtdichte. […] Unter Zugrundelegung dieser Empfindlichkeitskurve hat man 1940 in Deutschland die Dunkelleuchtdichte mit der Einheit Skot (sk) so festgesetzt, daß bei einem Licht der Farbtemperatur 2360 ° K 1 sk = 10 −3  asb gilt. 1948 ist von der Internationalen Beleuchtungskommission (IBK) die Bezugstemperatur auf 2046 °K, die Erstarrungstemperatur des Platins , festgesetzt worden. Die Bezeichnung Skot wurde von der IBK no übernommen, dafür soll "skotopisches Stilb" gesagt werden. Als höchstzulässiger Grenzwert für die Dunkelleuchtdichte ist in Deutschland 10 Skot festgesetzt worden, um eine Verwendung der Dunkelleuchtdichte im Gebiet des gemischten Zapfen - und Stäbchensehens zu vermeiden, da in diesem Bereich die photometrischen Maßgrößen wegen der allmählich itenden Augenempfindlichkeitskurve ihren Sinn verlieren. [...] Skot, abgek[ürzt] sk, Einheit für die Dunkelleuchtdichte, welche für zahlenmäßige Angaben und zum Anschluß der Dunkelleuchtdichte an die normale Leuchtdichte 1940 von der Deutschen Lichttechnischen Gesellschaft  [de] geschaffen wurde. Für diesen Anschluß wurde die Strahlung des schwarzen Körpers bei T  = 2360 °K, dh eine Strahlung der Farbtemperatur T 1  = 2360 °K vereinbart. Eine Lichtquelle strahlt mit der Dunkelleuchtdichte 1 sk, wenn sie photometrisch gleich einer Strahlung der Farbtemperatur T 2  = 2360 °K und der Leuchtdichte von 10 −3  asb (Apostilb) ist. Bei der Farbtemperatur T 1  = 2360 °K dorado también muere Relación: 1 sk = 10 −3  asb = 10 −7 /π sb.
  42. ^ "Resolución 4 de la 13ª CGPM (1967)". BIPM . Consultado el 21 de febrero de 2022 .
  43. ^ "Resolución 4: Definición de la unidad SI de temperatura termodinámica (kelvin)". Resoluciones de la 13ª CGPM . Bureau International des Poids et Mesures. 1967. Archivado desde el original el 2007-06-15 . Consultado el 2008-02-06 .
  44. ^ "Resolución 10 de la 23ª CGPM (2007)". BIPM . Consultado el 21 de febrero de 2022 .
  45. ^ "Unidad de temperatura termodinámica (kelvin)". Folleto del SI, 8.ª edición . Bureau International des Poids et Mesures. 1967. Sección 2.1.1.5. Archivado desde el original el 26 de septiembre de 2007. Consultado el 6 de febrero de 2008 .
  46. ^ por Ian Mills (29 de septiembre de 2010). "Borrador del capítulo 2 del folleto del SI, tras las redefiniciones de las unidades base" (PDF) . BIPM . CCU. Archivado desde el original (PDF) el 10 de enero de 2011 . Consultado el 1 de enero de 2011 .
  47. ^ "La Conferencia General de Pesas y Medidas aprueba posibles modificaciones del Sistema Internacional de Unidades, incluida la redefinición del kilogramo" (PDF) (Nota de prensa). Sèvres, Francia: Conferencia General de Pesas y Medidas . 23 de octubre de 2011. Archivado desde el original (PDF) el 9 de febrero de 2012. Consultado el 25 de octubre de 2011 .
  48. ^ Wood, B. (3–4 de noviembre de 2014). "Informe sobre la reunión del grupo de trabajo CODATA sobre constantes fundamentales" (PDF) . BIPM . p. 7. Archivado desde el original (PDF) el 13 de octubre de 2015. [El director del BIPM, Martin] Milton respondió a una pregunta sobre qué sucedería si... el CIPM o la CGPM votaran no seguir adelante con la redefinición de la SI. Respondió que sentía que para ese momento la decisión de seguir adelante debería verse como una conclusión inevitable.
  49. ^ "Valor CODATA 2022: constante de Boltzmann". Referencia del NIST sobre constantes, unidades e incertidumbre . NIST . Mayo de 2024. Consultado el 18 de mayo de 2024 .
  50. ^ ab «Resolución 1 de la 26ª CGPM (2018)». BIPM . Consultado el 21 de febrero de 2022 .
  51. ^ ab Newell, DB; Cabiati, F; Fischer, J; Fujii, K; Karshenboim, SG; Margolis, HS; de Mirandés, E; Mohr, PJ; Nez, F; Pachucki, K; Quinn, TJ; Taylor, BN; Wang, M; Wood, BM; Zhang, Z; et al. (Grupo de trabajo sobre constantes fundamentales del Comité de Datos para la Ciencia y la Tecnología (CODATA)) (2018-01-29). "Los valores de h, e, k y NA de CODATA 2017 para la revisión del SI". Metrologia . 55 (1): L13–L16. Bibcode : 2018Metro..55L..13N . doi : 10.1088/1681-7575/aa950a .
  52. ^ "Actualización de la definición del kelvin" (PDF) . BIPM . Archivado desde el original (PDF) el 2008-11-23 . Consultado el 2010-02-23 .
  53. ^ Fischer, J; Fellmuth, B; Gaiser, C; Zandt, T; Pitre, L; Sparasci, F; Plimmer, MD; de Podestá, M; Underwood, R; Sutton, G; Machín, G; Gavioso, RM; Madonna Ripa, D; Steur, PPM; Qu, J; Feng, XJ; Zhang, J; Moldover, señor; Benz, SP; Blanco, República Dominicana; Gianfrani, L; Castrillo, A; Moretti, L; Darquié, B; Moufarej, E; Daussy, C; Briaudeau, S; Kozlova, O; Risegari, L; Segovia, JJ; Martín, MC; del Campo, D (1 de abril de 2018). "El proyecto Boltzmann". Metrología . 55 (2): R1–R20. Código Bib : 2018Metro..55R...1F. doi :10.1088/1681-7575/aaa790. PMC 6508687. PMID 31080297  . 
  54. ^ "Guía del NIST para el SI | Capítulo 9: Reglas y convenciones de estilo para la ortografía de los nombres de las unidades", NIST SP 811 , 28 de enero de 2016. Una unidad derivada suele ser singular en inglés; por ejemplo, el valor 3 m 2 ·K/W suele escribirse como 'tres metros cuadrados kelvin por vatio', y el valor 3 C·m 2 /V suele escribirse como 'tres culombios metros cuadrados por voltio'. Sin embargo, una unidad 'simple' puede ser plural; por ejemplo, el valor 5 kPa se escribe como 'cinco kilopascales', aunque 'cinco kilopascales' es aceptable. Si en un caso de una sola unidad el número es menor que uno, la unidad siempre es singular cuando se escribe con todas sus letras; por ejemplo, 0,5 kPa se escribe como 'cinco décimas de kilopascal'.
  55. ^ "Definición de KELVIN". www.merriam-webster.com . Consultado el 21 de agosto de 2023 .
  56. ^ Guía de estilo del idioma inglés del CERN (PDF) . CERN . 2022. pág. 64.
  57. ^ "Escritura con unidades del SI (sistema métrico)". NIST . 13 de enero de 2010.
  58. ^ Brady, James E.; Senese, Fred (28 de enero de 2008). Química, Guía de estudio para estudiantes: El estudio de la materia y sus cambios. John Wiley & Sons. pág. 15. ISBN 978-0-470-18464-6.
  59. ^ "22.2". El estándar Unicode, versión 8.0 (PDF) . Mountain View, CA, EE. UU.: The Unicode Consortium. Agosto de 2015. ISBN 978-1-936213-10-8Archivado (PDF) del original el 6 de diciembre de 2016. Consultado el 6 de septiembre de 2015 .

Bibliografía

  • Bureau International des Poids et Mesures (2019). "El folleto del Sistema Internacional de Unidades (SI)" (PDF) . Novena edición. Comité Internacional de Pesas y Medidas . Consultado el 28 de abril de 2022 .
  • Thomson, William (Lord Kelvin) (1882). Documentos matemáticos y físicos: Volumen I. Cambridge University Press.
Busque kelvin en Wikcionario, el diccionario libre.
  • Thomson, William (octubre de 1848). «Sobre una escala termométrica absoluta fundada en la teoría de la fuerza motriz del calor de Carnot y calculada a partir de las observaciones de Regnault». zapatopi.net . Revista filosófica. Archivado desde el original el 2008-02-01 . Consultado el 2022-02-21 .
  • Thomson, William (marzo de 1851). "Sobre la teoría dinámica del calor, con resultados numéricos deducidos del equivalente de una unidad térmica del señor Joule y las observaciones de M. Regnault sobre el vapor". zapatopi.net . Transacciones de la Royal Society de Edimburgo . Consultado el 5 de mayo de 2024 .
Retrieved from "https://en.wikipedia.org/w/index.php?title=Kelvin&oldid=1250969846"