Energía mecánica

En las ciencias físicas , la energía mecánica es la suma de la energía potencial y la energía cinética . El principio de conservación de la energía mecánica establece que si un sistema aislado está sujeto únicamente a fuerzas conservativas , entonces la energía mecánica es constante. Si un objeto se mueve en la dirección opuesta de una fuerza neta conservativa, la energía potencial aumentará; y si la rapidez (no la velocidad ) del objeto cambia, la energía cinética del objeto también cambia. Sin embargo, en todos los sistemas reales, estarán presentes fuerzas no conservativas , como las fuerzas de fricción , pero si son de magnitud despreciable , la energía mecánica cambia poco y su conservación es una aproximación útil. En las colisiones elásticas , la energía cinética se conserva, pero en las colisiones inelásticas, parte de la energía mecánica puede convertirse en energía térmica . La equivalencia entre la energía mecánica perdida y un aumento de la temperatura fue descubierta por James Prescott Joule .

Se utilizan muchos dispositivos para convertir energía mecánica en o desde otras formas de energía , por ejemplo, un motor eléctrico convierte energía eléctrica en energía mecánica, un generador eléctrico convierte energía mecánica en energía eléctrica y un motor térmico convierte calor en energía mecánica.

La energía es una cantidad escalar y la energía mecánica de un sistema es la suma de la energía potencial (que se mide por la posición de las partes del sistema) y la energía cinética (que también se llama energía de movimiento): ^{[1] [2]}

$${\displaystyle E_{\text{mecánica}}=U+K}$$

La energía potencial, U , depende de la posición de un objeto sometido a la gravedad o a alguna otra fuerza conservativa . La energía potencial gravitatoria de un objeto es igual al peso W del objeto multiplicado por la altura h del centro de gravedad del objeto con respecto a un punto de referencia arbitrario:

$${\displaystyle U=Wh}$$

La energía potencial de un objeto se puede definir como la capacidad del objeto para realizar trabajo y aumenta a medida que el objeto se mueve en la dirección opuesta a la dirección de la fuerza. ^{[nb 1] [1]} Si F representa la fuerza conservativa y x la posición, la energía potencial de la fuerza entre las dos posiciones x ₁ y x ₂ se define como la integral negativa de F de x ₁ a x ₂ : ^[4]

$${\displaystyle U=-\int _{x_{1}}^{x_{2}}{\vec {F}}\cdot d{\vec {x}}}$$

La energía cinética, K , depende de la velocidad de un objeto y es la capacidad de un objeto en movimiento de realizar trabajo sobre otros objetos cuando choca con ellos. ^{[nb 2] [8]} Se define como la mitad del producto de la masa del objeto por el cuadrado de su velocidad, y la energía cinética total de un sistema de objetos es la suma de las energías cinéticas de los respectivos objetos: ^{[1] [9]}

$${\displaystyle K={1 \sobre 2}mv^{2}}$$

El principio de conservación de la energía mecánica establece que si un cuerpo o sistema está sometido únicamente a fuerzas conservativas , la energía mecánica de ese cuerpo o sistema permanece constante. ^[10] La diferencia entre una fuerza conservativa y una no conservativa es que cuando una fuerza conservativa mueve un objeto de un punto a otro, el trabajo realizado por la fuerza conservativa es independiente de la trayectoria. Por el contrario, cuando una fuerza no conservativa actúa sobre un objeto, el trabajo realizado por la fuerza no conservativa depende de la trayectoria. ^{[11] [12]}

Según el principio de conservación de la energía mecánica, la energía mecánica de un sistema aislado permanece constante en el tiempo, siempre que el sistema esté libre de fricción y otras fuerzas no conservativas. En cualquier situación real, las fuerzas de fricción y otras fuerzas no conservativas están presentes, pero en muchos casos sus efectos sobre el sistema son tan pequeños que el principio de conservación de la energía mecánica puede utilizarse como una aproximación justa . Aunque la energía no puede crearse ni destruirse, puede convertirse en otra forma de energía. ^{[1] [13]}

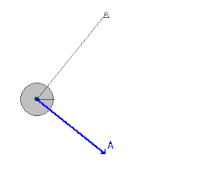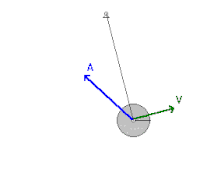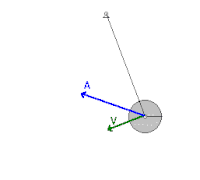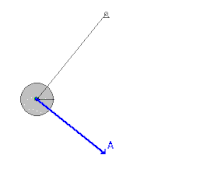
En un sistema mecánico como un péndulo oscilante sometido a la fuerza gravitacional conservativa , donde las fuerzas de fricción como la resistencia del aire y la fricción en el pivote son despreciables, la energía pasa de ida y vuelta entre la energía cinética y la potencial, pero nunca abandona el sistema. El péndulo alcanza su máxima energía cinética y su mínima energía potencial cuando está en posición vertical, porque tendrá la mayor velocidad y estará más cerca de la Tierra en ese punto. Por otro lado, tendrá su menor energía cinética y su mayor energía potencial en las posiciones extremas de su oscilación, porque tiene velocidad cero y está más alejado de la Tierra en esos puntos. Sin embargo, al tener en cuenta las fuerzas de fricción, el sistema pierde energía mecánica con cada oscilación debido al trabajo negativo realizado sobre el péndulo por estas fuerzas no conservativas. ^[2]

Hace ya mucho tiempo que se sabe que la pérdida de energía mecánica en un sistema siempre da como resultado un aumento de la temperatura del sistema, pero fue el físico aficionado James Prescott Joule quien demostró por primera vez experimentalmente cómo una cierta cantidad de trabajo realizado contra la fricción daba como resultado una cantidad definida de calor que debe concebirse como los movimientos aleatorios de las partículas que componen la materia. ^[14] Esta equivalencia entre energía mecánica y calor es especialmente importante cuando se consideran objetos en colisión. En una colisión elástica , la energía mecánica se conserva: la suma de las energías mecánicas de los objetos en colisión es la misma antes y después de la colisión. Sin embargo, después de una colisión inelástica , la energía mecánica del sistema habrá cambiado. Por lo general, la energía mecánica antes de la colisión es mayor que la energía mecánica después de la colisión. En las colisiones inelásticas, parte de la energía mecánica de los objetos en colisión se transforma en energía cinética de las partículas constituyentes. Este aumento de la energía cinética de las partículas constituyentes se percibe como un aumento de la temperatura. La colisión se puede describir diciendo que parte de la energía mecánica de los objetos que chocan se ha convertido en una cantidad igual de calor. Por lo tanto, la energía total del sistema permanece inalterada aunque la energía mecánica del sistema se haya reducido. ^{[1] [15]}

Un satélite de masa a cierta distancia del centro de la Tierra posee tanto energía cinética, , (en virtud de su movimiento) como energía potencial gravitatoria, , (en virtud de su posición dentro del campo gravitatorio de la Tierra; la masa de la Tierra es ). Por lo tanto, la energía mecánica del sistema satélite-Tierra está dada por${\estilo de visualización m}$${\estilo de visualización r}$${\estilo de visualización K}$${\estilo de visualización U}$${\estilo de visualización M}$${\displaystyle E_{\text{mecánico}}}$$${\displaystyle E_{\text{mecánica}}=U+K}$$$${\displaystyle E_{\text{mecánica}}=-G{\frac {Mm}{r}}\ +{\frac {1}{2}}\,mv^{2}}$$

Si el satélite está en órbita circular, la ecuación de conservación de energía se puede simplificar aún más: ya que en el movimiento circular, la segunda ley de movimiento de Newton se puede tomar como$${\displaystyle E_{\text{mecánica}}=-G{\frac {Mm}{2r}}}$$$${\displaystyle G{\frac {Mm}{r^{2}}}\ ={\frac {mv^{2}}{r}}}$$

En la actualidad, existen numerosos dispositivos tecnológicos que convierten la energía mecánica en otras formas de energía o viceversa. Estos dispositivos pueden clasificarse en las siguientes categorías:

• Un motor eléctrico convierte energía eléctrica en energía mecánica. ^{[16] [17] [18]}
• Un generador convierte energía mecánica en energía eléctrica. ^[19]
• Una central hidroeléctrica convierte la energía mecánica del agua en una presa de almacenamiento en energía eléctrica. ^[20]
• Un motor de combustión interna es un motor térmico que obtiene energía mecánica a partir de energía química quemando combustible . A partir de esta energía mecánica, el motor de combustión interna suele generar electricidad. ^[21]
• Una máquina de vapor convierte la energía térmica del vapor en energía mecánica. ^[22]
• Una turbina convierte la energía cinética de una corriente de gas o líquido en energía mecánica. ^[23]

La clasificación de la energía en diferentes tipos a menudo sigue los límites de los campos de estudio de las ciencias naturales.

• La energía química es el tipo de energía potencial "almacenada" en los enlaces químicos y se estudia en química . ^[24]
• La energía nuclear es la energía almacenada en las interacciones entre las partículas del núcleo atómico y se estudia en la física nuclear . ^[25]
• La energía electromagnética se presenta en forma de cargas eléctricas, campos magnéticos y fotones . Se estudia en el electromagnetismo . ^{[26] [27]}
• Diversas formas de energía en la mecánica cuántica ; por ejemplo, los niveles de energía de los electrones en un átomo. ^{[28] [29]}

Notas

Citas

Bibliografía

• Brodie, David; Brown, Wendy; Heslop, Nigel; Ireson, Gren; Williams, Peter (1998). Terry Parkin (ed.). Física . Addison Wesley Longman Limited. ISBN 978-0-582-28736-5.
• Jain, Mahesh C. (2009). Libro de texto de ingeniería física, parte I. Nueva Delhi: PHI Learning Pvt. Ltd. ISBN 978-81-203-3862-3. Consultado el 25 de agosto de 2011 .
• Newton, Isaac (1999). I. Bernard Cohen; Anne Miller Whitman (eds.). Los Principia: principios matemáticos de la filosofía natural . Estados Unidos de América: University of California Press. ISBN 978-0-520-08816-0.