Matriz de rotación

En álgebra lineal , una matriz de rotación es una matriz de transformación que se utiliza para realizar una rotación en el espacio euclidiano . Por ejemplo, utilizando la convención siguiente, la matriz

${\displaystyle R={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}}$

rota puntos en el plano xy en sentido antihorario a través de un ángulo θ alrededor del origen de un sistema de coordenadas cartesianas bidimensionales . Para realizar la rotación en un punto del plano con coordenadas estándar v = ( x , y ) , debe escribirse como un vector columna y multiplicarse por la matriz R :

${\displaystyle R\mathbf {v} ={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}{\begin{bmatrix}x \\y\end{bmatrix}}={\begin{bmatrix}x\cos \theta -y\sin \theta \\x\sin \theta +y\cos \theta \end{bmatrix}}.}$

Si x e y son las coordenadas de los extremos de un vector, donde x es coseno e y es seno, entonces las ecuaciones anteriores se convierten en las fórmulas trigonométricas de suma de ángulos . De hecho, una matriz de rotación puede verse como las fórmulas trigonométricas de suma de ángulos en forma matricial. Una forma de entender esto es decir que tenemos un vector en un ángulo de 30° desde el eje x , y deseamos rotar ese ángulo otros 45°. Simplemente necesitamos calcular las coordenadas del extremo del vector en 75°.

Los ejemplos de este artículo se aplican a rotaciones activas de vectores en sentido antihorario en un sistema de coordenadas diestro ( y en sentido antihorario desde x ) por premultiplicación ( R a la izquierda). Si se cambia alguno de estos (como rotar ejes en lugar de vectores, una transformación pasiva ), entonces se debe utilizar la inversa de la matriz de ejemplo, que coincide con su transpuesta .

Dado que la multiplicación de matrices no tiene efecto sobre el vector cero (las coordenadas del origen), las matrices de rotación describen rotaciones sobre el origen. Las matrices de rotación proporcionan una descripción algebraica de dichas rotaciones y se utilizan ampliamente para cálculos en geometría , física y gráficos por computadora . En alguna literatura, el término rotación se generaliza para incluir rotaciones impropias , caracterizadas por matrices ortogonales con un determinante de −1 (en lugar de +1). Estas combinan rotaciones propias con reflexiones (que invierten la orientación ). En otros casos, donde no se consideran las reflexiones, se puede omitir la etiqueta de propias . Esta última convención se sigue en este artículo.

Las matrices de rotación son matrices cuadradas , con entradas reales . Más específicamente, se pueden caracterizar como matrices ortogonales con determinante  1; es decir, una matriz cuadrada R es una matriz de rotación si y solo si R ^T = R ⁻¹ y det R = 1 . El conjunto de todas las matrices ortogonales de tamaño n con determinante +1 es una representación de un grupo conocido como el grupo ortogonal especial SO( n ) , un ejemplo del cual es el grupo de rotación SO(3) . El conjunto de todas las matrices ortogonales de tamaño n con determinante +1 o −1 es una representación del grupo ortogonal (general) O( n ) .

En dos dimensiones, la matriz de rotación estándar tiene la siguiente forma:

${\displaystyle R(\theta )={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}.}$

Esto rota los vectores columna mediante la siguiente multiplicación de matrices ,

${\displaystyle {\begin{bmatrix}x'\\y'\\\end{bmatrix}}={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \\\end{bmatrix}}{\begin{bmatrix}x\\y\\\end{bmatrix}}.}$

Por lo tanto, las nuevas coordenadas ( x ′, y ′) de un punto ( x , y ) después de la rotación son

${\displaystyle {\begin{aligned}x'&=x\cos \theta -y\sin \theta \,\\y'&=x\sin \theta +y\cos \theta \,\end{aligned}}.}$

Por ejemplo, cuando el vector

${\displaystyle \mathbf {\hat {x}} ={\begin{bmatrix}1\\0\\\end{bmatrix}}}$

se gira un ángulo θ , sus nuevas coordenadas son

${\displaystyle {\begin{bmatrix}\cos \theta \\\sin \theta \\\end{bmatrix}},}$

y cuando el vector

${\displaystyle \mathbf {\hat {y}} ={\begin{bmatrix}0\\1\\\end{bmatrix}}}$

se gira un ángulo θ , sus nuevas coordenadas son

${\displaystyle {\begin{bmatrix}-\sin \theta \\\cos \theta \\\end{bmatrix}}.}$

La dirección de rotación del vector es en sentido antihorario si θ es positivo (por ejemplo, 90°) y en sentido horario si θ es negativo (por ejemplo, −90°) para . Por lo tanto, la matriz de rotación en sentido horario se obtiene como${\displaystyle R(\theta )}$

${\displaystyle R(-\theta )={\begin{bmatrix}\cos \theta &\sin \theta \\-\sin \theta &\cos \theta \\\end{bmatrix}}.}$

El caso bidimensional es el único caso no trivial (es decir, no unidimensional) en el que el grupo de matrices de rotación es conmutativo, de modo que no importa en qué orden se realizan las rotaciones múltiples. Una convención alternativa utiliza ejes rotatorios, ^[1] y las matrices anteriores también representan una rotación de los ejes en el sentido de las agujas del reloj a través de un ángulo θ .

Si se utiliza un sistema de coordenadas cartesiano estándar para diestros , con el eje x a la derecha y el eje y hacia arriba, la rotación R ( θ ) es en sentido antihorario. Si se utiliza un sistema de coordenadas cartesiano para zurdos, con x dirigida a la derecha pero y dirigida hacia abajo, R ( θ ) es en el sentido de las agujas del reloj. Estas orientaciones no estándar rara vez se utilizan en matemáticas, pero son comunes en gráficos de computadora 2D , que a menudo tienen el origen en la esquina superior izquierda y el eje y hacia abajo en la pantalla o página. ^[2]

Consulte a continuación otras convenciones alternativas que pueden cambiar el sentido de la rotación producida por una matriz de rotación.

Especialmente útiles son las matrices

${\displaystyle {\begin{bmatrix}0&-1\\[3pt]1&0\\\end{bmatrix}},\quad {\begin{bmatrix}-1&0\\[3pt]0&-1\\\end{bmatrix}},\quad {\begin{bmatrix}0&1\\[3pt]-1&0\\\end{bmatrix}}}$

para rotaciones en sentido antihorario de 90°, 180° y 270°.

Desde

${\displaystyle {\begin{bmatrix}0&-1\\1&0\end{bmatrix}}^{2}\ =\ {\begin{bmatrix}-1&0\\0&-1\end{bmatrix}}\ =-I,}$

Las matrices de la forma

${\displaystyle {\begin{bmatrix}x&-y\\y&x\end{bmatrix}}}$

forman un anillo isomorfo al cuerpo de los números complejos ⁠ ⁠${\displaystyle \mathbb {C} }$ . Bajo este isomorfismo, las matrices de rotación corresponden al círculo de los números complejos unitarios , los números complejos de módulo 1 .

Si se identifica con a través del isomorfismo lineal la acción de una matriz de la forma anterior sobre vectores de corresponde a la multiplicación por el número complejo x + iy , y las rotaciones corresponden a la multiplicación por números complejos de módulo 1 .${\displaystyle \mathbb {R} ^{2}}$${\displaystyle \mathbb {C} }$ ${\displaystyle (a,b)\mapsto a+ib,}$${\displaystyle \mathbb {R} ^{2}}$

Como toda matriz de rotación se puede escribir

${\displaystyle {\begin{pmatrix}\cos t&-\sin t\\\sin t&\cos t\end{pmatrix}},}$

La correspondencia anterior asocia dicha matriz con el número complejo

${\displaystyle \cos t+i\sin t=e^{it}}$

(esta última igualdad es la fórmula de Euler ).

Una rotación 3D básica (también llamada rotación elemental) es una rotación sobre uno de los ejes de un sistema de coordenadas. Las siguientes tres matrices de rotación básicas rotan vectores en un ángulo θ sobre el eje x , y o z , en tres dimensiones, utilizando la regla de la mano derecha , que codifica sus signos alternos. Observe que la regla de la mano derecha solo funciona cuando se multiplican . (Las mismas matrices también pueden representar una rotación en el sentido de las agujas del reloj de los ejes. ^{[nb 1]} )${\displaystyle R\cdot {\vec {x}}}$

${\displaystyle {\begin{alignedat}{1}R_{x}(\theta )&={\begin{bmatrix}1&0&0\\0&\cos \theta &-\sin \theta \\[3pt]0&\sin \theta &\cos \theta \\[3pt]\end{bmatrix}}\\[6pt]R_{y}(\theta )&={\begin{bmatrix}\cos \theta &0&\sin \theta \\[3pt]0&1&0\\[3pt]-\sin \theta &0&\cos \theta \\\end{bmatrix}}\\[6pt]R_{z}(\theta )&={\begin{bmatrix}\cos \theta &-\sin \theta &0\\[3pt]\sin \theta &\cos \theta &0\\[3pt]0&0&1\\\end{bmatrix}}\end{alignedat}}}$

En el caso de los vectores columna , cada una de estas rotaciones básicas de vector aparece en sentido antihorario cuando el eje sobre el que se producen apunta hacia el observador, el sistema de coordenadas es diestro y el ángulo θ es positivo. R _z , por ejemplo, rotaría hacia el eje y un vector alineado con el eje x , como se puede comprobar fácilmente operando con R _z sobre el vector (1,0,0) :

${\displaystyle R_{z}(90^{\circ }){\begin{bmatrix}1\\0\\0\\\end{bmatrix}}={\begin{bmatrix}\cos 90^{\circ }&-\sin 90^{\circ }&0\\\sin 90^{\circ }&\quad \cos 90^{\circ }&0\\0&0&1\\\end{bmatrix}}{\begin{bmatrix}1\\0\\0\\\end{bmatrix}}={\begin{bmatrix}0&-1&0\\1&0&0\\0&0&1\\\end{bmatrix}}{\begin{bmatrix}1\\0\\0\\\end{bmatrix}}={\begin{bmatrix}0\\1\\0\\\end{bmatrix}}}$

Esto es similar a la rotación producida por la matriz de rotación bidimensional mencionada anteriormente. Vea a continuación convenciones alternativas que pueden, aparentemente o en realidad, invertir el sentido de la rotación producida por estas matrices.

Se pueden obtener otras matrices de rotación 3D a partir de estas tres mediante la multiplicación de matrices . Por ejemplo, el producto

${\displaystyle {\begin{aligned}R=R_{z}(\alpha )\,R_{y}(\beta )\,R_{x}(\gamma )&={\overset {\text{yaw}}{\begin{bmatrix}\cos \alpha &-\sin \alpha &0\\\sin \alpha &\cos \alpha &0\\0&0&1\\\end{bmatrix}}}{\overset {\text{pitch}}{\begin{bmatrix}\cos \beta &0&\sin \beta \\0&1&0\\-\sin \beta &0&\cos \beta \\\end{bmatrix}}}{\overset {\text{roll}}{\begin{bmatrix}1&0&0\\0&\cos \gamma &-\sin \gamma \\0&\sin \gamma &\cos \gamma \\\end{bmatrix}}}\\&={\begin{bmatrix}\cos \alpha \cos \beta &\cos \alpha \sin \beta \sin \gamma -\sin \alpha \cos \gamma &\cos \alpha \sin \beta \cos \gamma +\sin \alpha \sin \gamma \\\sin \alpha \cos \beta &\sin \alpha \sin \beta \sin \gamma +\cos \alpha \cos \gamma &\sin \alpha \sin \beta \cos \gamma -\cos \alpha \sin \gamma \\-\sin \beta &\cos \beta \sin \gamma &\cos \beta \cos \gamma \\\end{bmatrix}}\end{aligned}}}$

representa una rotación cuyos ángulos de guiñada, cabeceo y balanceo son α , β y γ , respectivamente. Más formalmente, es una rotación intrínseca cuyos ángulos de Tait-Bryan son α , β , γ , alrededor de los ejes z , y , x , respectivamente. De manera similar, el producto

${\displaystyle {\begin{aligned}\\R=R_{z}(\gamma )\,R_{y}(\beta )\,R_{x}(\alpha )&={\overset {\text{roll}}{\begin{bmatrix}\cos \gamma &-\sin \gamma &0\\\sin \gamma &\cos \gamma &0\\0&0&1\\\end{bmatrix}}}{\overset {\text{pitch}}{\begin{bmatrix}\cos \beta &0&\sin \beta \\0&1&0\\-\sin \beta &0&\cos \beta \\\end{bmatrix}}}{\overset {\text{yaw}}{\begin{bmatrix}1&0&0\\0&\cos \alpha &-\sin \alpha \\0&\sin \alpha &\cos \alpha \\\end{bmatrix}}}\\&={\begin{bmatrix}\cos \beta \cos \gamma &\sin \alpha \sin \beta \cos \gamma -\cos \alpha \sin \gamma &\cos \alpha \sin \beta \cos \gamma +\sin \alpha \sin \gamma \\\cos \beta \sin \gamma &\sin \alpha \sin \beta \sin \gamma +\cos \alpha \cos \gamma &\cos \alpha \sin \beta \sin \gamma -\sin \alpha \cos \gamma \\-\sin \beta &\sin \alpha \cos \beta &\cos \alpha \cos \beta \\\end{bmatrix}}\end{aligned}}}$

representa una rotación extrínseca cuyos ángulos de Euler (impropios) son α , β , γ , alrededor de los ejes x , y , z .

Estas matrices producen el efecto deseado sólo si se utilizan para premultiplicar vectores columna y (ya que en general la multiplicación de matrices no es conmutativa ) sólo si se aplican en el orden especificado (ver Ambigüedades para más detalles). El orden de las operaciones de rotación es de derecha a izquierda; la matriz adyacente al vector columna es la primera en aplicarse, y luego la de la izquierda. ^[3]

Cada rotación en tres dimensiones está definida por su eje (un vector a lo largo de este eje no cambia con la rotación) y su ángulo , la cantidad de rotación alrededor de ese eje ( teorema de rotación de Euler ).

Existen varios métodos para calcular el eje y el ángulo a partir de una matriz de rotación (véase también la representación eje-ángulo ). Aquí, solo describimos el método basado en el cálculo de los vectores y valores propios de la matriz de rotación. También es posible utilizar la traza de la matriz de rotación.

Dada una matriz de rotación R de 3 × 3 , un vector u paralelo al eje de rotación debe satisfacer

${\displaystyle R\mathbf {u} =\mathbf {u} ,}$

ya que la rotación de u alrededor del eje de rotación debe dar como resultado u . La ecuación anterior se puede resolver para u , que es único hasta un factor escalar a menos que R = I .

Además, la ecuación puede reescribirse

${\displaystyle R\mathbf {u} =I\mathbf {u} \implies \left(R-I\right)\mathbf {u} =0,}$

lo que demuestra que u se encuentra en el espacio nulo de R − I .

Visto de otra manera, u es un vector propio de R correspondiente al valor propio λ = 1. Toda matriz de rotación debe tener este valor propio, siendo los otros dos valores propios conjugados complejos entre sí. De ello se deduce que una matriz de rotación general en tres dimensiones tiene, salvo una constante multiplicativa, un solo vector propio real.

Una forma de determinar el eje de rotación es demostrando que:

${\displaystyle {\begin{aligned}0&=R^{\mathsf {T}}0+0\\&=R^{\mathsf {T}}\left(R-I\right)\mathbf {u} +\left(R-I\right)\mathbf {u} \\&=\left(R^{\mathsf {T}}R-R^{\mathsf {T}}+R-I\right)\mathbf {u} \\&=\left(I-R^{\mathsf {T}}+R-I\right)\mathbf {u} \\&=\left(R-R^{\mathsf {T}}\right)\mathbf {u} \end{aligned}}}$

Dado que ( R − R ^T ) es una matriz antisimétrica , podemos elegir u tal que

${\displaystyle [\mathbf {u} ]_{\times }=\left(R-R^{\mathsf {T}}\right).}$

El producto matriz-vector se convierte en un producto vectorial de un vector consigo mismo, lo que garantiza que el resultado sea cero:

${\displaystyle \left(R-R^{\mathsf {T}}\right)\mathbf {u} =[\mathbf {u} ]_{\times }\mathbf {u} =\mathbf {u} \times \mathbf {u} =0\,}$

Por lo tanto, si

${\displaystyle R={\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\\\end{bmatrix}},}$

entonces

${\displaystyle \mathbf {u} ={\begin{bmatrix}h-f\\c-g\\d-b\\\end{bmatrix}}.}$

La magnitud de u calculada de esta manera es ‖ u ‖ = 2 sen θ , donde θ es el ángulo de rotación.

Esto no funciona si R es simétrico. En el caso anterior, si R − R ^T es cero, todos los pasos subsiguientes son inválidos. En este caso, es necesario diagonalizar R y encontrar el vector propio correspondiente a un valor propio de 1.

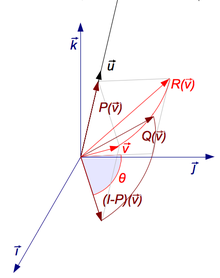
Para hallar el ángulo de una rotación, una vez conocido el eje de rotación, se selecciona un vector v perpendicular al eje. Entonces el ángulo de rotación es el ángulo entre v y R v .

Sin embargo, un método más directo consiste en calcular simplemente la traza : la suma de los elementos diagonales de la matriz de rotación. Se debe tener cuidado de seleccionar el signo correcto para el ángulo θ para que coincida con el eje elegido:

${\displaystyle \operatorname {tr} (R)=1+2\cos \theta ,}$

de lo cual se deduce que el valor absoluto del ángulo es

${\displaystyle |\theta |=\arccos \left({\frac {\operatorname {tr} (R)-1}{2}}\right).}$

Para el eje de rotación , puede obtener el ángulo correcto ^[4] a partir de${\displaystyle \mathbf {n} =(n_{1},n_{2},n_{3})}$

${\displaystyle \left\{{\begin{matrix}\cos \theta &=&{\dfrac {\operatorname {tr} (R)-1}{2}}\\\sin \theta &=&-{\dfrac {\operatorname {tr} (K_{n}R)}{2}}\end{matrix}}\right.}$

dónde

${\displaystyle K_{n}={\begin{bmatrix}0&-n_{3}&n_{2}\\n_{3}&0&-n_{1}\\-n_{2}&n_{1}&0\\\end{bmatrix}}}$

La matriz de una rotación propia R por un ángulo θ alrededor del eje u = ( u _x , u _y , u _z ) , un vector unitario con u^2x
_​+ tú²
_años+ tú^2z
_​= 1 , viene dado por: ^{[5] [6] [7] [8]}

${\displaystyle R={\begin{bmatrix}u_{x}^{2}\left(1-\cos \theta \right)+\cos \theta &u_{x}u_{y}\left(1-\cos \theta \right)-u_{z}\sin \theta &u_{x}u_{z}\left(1-\cos \theta \right)+u_{y}\sin \theta \\u_{x}u_{y}\left(1-\cos \theta \right)+u_{z}\sin \theta &u_{y}^{2}\left(1-\cos \theta \right)+\cos \theta &u_{y}u_{z}\left(1-\cos \theta \right)-u_{x}\sin \theta \\u_{x}u_{z}\left(1-\cos \theta \right)-u_{y}\sin \theta &u_{y}u_{z}\left(1-\cos \theta \right)+u_{x}\sin \theta &u_{z}^{2}\left(1-\cos \theta \right)+\cos \theta \end{bmatrix}}.}$

Una derivación de esta matriz a partir de los primeros principios se puede encontrar en la sección 9.2 aquí. ^[9] La idea básica para derivar esta matriz es dividir el problema en unos pocos pasos simples conocidos.

1. Primero gire el eje dado y el punto de manera que el eje se encuentre en uno de los planos de coordenadas ( xy , yz o zx ).
2. Luego, gire el eje dado y el punto de manera que el eje esté alineado con uno de los dos ejes de coordenadas para ese plano de coordenadas en particular ( x , y o z ).
3. Utilice una de las matrices de rotación fundamentales para rotar el punto dependiendo del eje de coordenadas con el que está alineado el eje de rotación.
4. Gire en sentido inverso el par eje-punto de modo que alcance la configuración final que tenía en el paso 2 (deshaciendo el paso 2)
5. Gire en sentido inverso el par eje-punto que se realizó en el paso 1 (deshaciendo el paso 1)

Esto se puede escribir de forma más concisa como ^[10]

${\displaystyle R=(\cos \theta )\,I+(\sin \theta )\,[\mathbf {u} ]_{\times }+(1-\cos \theta )\,(\mathbf {u} \otimes \mathbf {u} ),}$

donde [ u ] _× es la matriz de producto vectorial de u ; la expresión u ⊗ u es el producto externo e I es la matriz identidad . Alternativamente, las entradas de la matriz son:

${\displaystyle R_{jk}={\begin{cases}\cos ^{2}{\frac {\theta }{2}}+\sin ^{2}{\frac {\theta }{2}}\left(2u_{j}^{2}-1\right),\quad &{\text{if }}j=k\\2u_{j}u_{k}\sin ^{2}{\frac {\theta }{2}}-\varepsilon _{jkl}u_{l}\sin \theta ,\quad &{\text{if }}j\neq k\end{cases}}}$

donde ε _jkl es el símbolo de Levi-Civita con ε ₁₂₃ = 1. Esta es una forma matricial de la fórmula de rotación de Rodrigues (o la fórmula de Euler-Rodrigues equivalente, parametrizada de manera diferente ) con ^{[nb 2]}

${\displaystyle \mathbf {u} \otimes \mathbf {u} =\mathbf {u} \mathbf {u} ^{\mathsf {T}}={\begin{bmatrix}u_{x}^{2}&u_{x}u_{y}&u_{x}u_{z}\\[3pt]u_{x}u_{y}&u_{y}^{2}&u_{y}u_{z}\\[3pt]u_{x}u_{z}&u_{y}u_{z}&u_{z}^{2}\end{bmatrix}},\qquad [\mathbf {u} ]_{\times }={\begin{bmatrix}0&-u_{z}&u_{y}\\[3pt]u_{z}&0&-u_{x}\\[3pt]-u_{y}&u_{x}&0\end{bmatrix}}.}$

En la rotación de un vector x alrededor del eje u un ángulo θ se puede escribir como:${\displaystyle \mathbb {R} ^{3}}$

${\displaystyle R_{\mathbf {u} }(\theta )\mathbf {x} =\mathbf {u} (\mathbf {u} \cdot \mathbf {x} )+\cos \left(\theta \right)(\mathbf {u} \times \mathbf {x} )\times \mathbf {u} +\sin \left(\theta \right)(\mathbf {u} \times \mathbf {x} )}$

o equivalentemente:

${\displaystyle R_{\mathbf {u} }(\theta )\mathbf {x} =\mathbf {x} \cos(\theta )+\mathbf {u} (\mathbf {x} \cdot \mathbf {u} )(1-\cos(\theta ))-\mathbf {x} \times \mathbf {u} \sin {\theta }}$

Esto también se puede escribir en notación tensorial como: ^[11]

${\displaystyle (R_{\mathbf {u} }(\theta )\mathbf {x} )_{i}=(R_{\mathbf {u} }(\theta ))_{ij}{\mathbf {x} }_{j}\quad {\text{with}}\quad (R_{\mathbf {u} }(\theta ))_{ij}=\delta _{ij}\cos(\theta )+\mathbf {u} _{i}\mathbf {u} _{j}(1-\cos(\theta ))-\sin {\theta }\varepsilon _{ijk}\mathbf {u} _{k}}$

Si el espacio 3D es dextrógiro y θ > 0 , esta rotación será en sentido antihorario cuando u apunte hacia el observador ( regla de la mano derecha ). Explícitamente, con una base ortonormal dextrógira,${\displaystyle ({\boldsymbol {\alpha }},{\boldsymbol {\beta }},\mathbf {u} )}$

${\displaystyle R_{\mathbf {u} }(\theta ){\boldsymbol {\alpha }}=\cos \left(\theta \right){\boldsymbol {\alpha }}+\sin \left(\theta \right){\boldsymbol {\beta }},\quad R_{\mathbf {u} }(\theta ){\boldsymbol {\beta }}=-\sin \left(\theta \right){\boldsymbol {\alpha }}+\cos \left(\theta \right){\boldsymbol {\beta }},\quad R_{\mathbf {u} }(\theta )\mathbf {u} =\mathbf {u} .}$

Obsérvense las sorprendentes diferencias, meramente aparentes, con la formulación algebraica de Lie equivalente que aparece a continuación.

Para cualquier matriz de rotación n -dimensional R que actúa sobre${\displaystyle \mathbb {R} ^{n},}$

${\displaystyle R^{\mathsf {T}}=R^{-1}}$(La rotación es una matriz ortogonal )

Resulta que:

${\displaystyle \det R=\pm 1}$

Una rotación se denomina propia si det R = 1 , e impropia (o roto-reflexión) si det R = –1 . Para dimensiones pares n = 2 k , los n valores propios λ de una rotación propia ocurren como pares de conjugados complejos que son raíces de la unidad: λ = e ^{± iθ _j} para j = 1, ..., k , que es real solo para λ = ±1 . Por lo tanto, puede que no haya vectores fijados por la rotación ( λ = 1 ), y por lo tanto no hay eje de rotación. Cualquier vector propio fijo ocurre en pares, y el eje de rotación es un subespacio de dimensión par.

Para dimensiones impares n = 2 k + 1 , una rotación propia R tendrá un número impar de valores propios, con al menos un λ = 1 y el eje de rotación será un subespacio de dimensión impar. Demostración:

${\displaystyle {\begin{aligned}\det \left(R-I\right)&=\det \left(R^{\mathsf {T}}\right)\det \left(R-I\right)=\det \left(R^{\mathsf {T}}R-R^{\mathsf {T}}\right)=\det \left(I-R^{\mathsf {T}}\right)\\&=\det(I-R)=\left(-1\right)^{n}\det \left(R-I\right)=-\det \left(R-I\right).\end{aligned}}}$

Aquí I es la matriz identidad, y usamos det( R ^T ) = det( R ) = 1 , así como (−1) ⁿ = −1 ya que n es impar. Por lo tanto, det( R – I ) = 0 , lo que significa que hay un vector distinto de cero v con ( R – I ) v = 0 , es decir R v = v , un vector propio fijo. También puede haber pares de vectores propios fijos en el subespacio de dimensión par ortogonal a v , por lo que la dimensión total de los vectores propios fijos es impar.

Por ejemplo, en el 2-espacio n = 2 , una rotación por un ángulo θ tiene valores propios λ = e ^iθ y λ = e ^{− iθ} , por lo que no hay eje de rotación excepto cuando θ = 0 , el caso de la rotación nula. En el 3-espacio n = 3 , el eje de una rotación propia no nula es siempre una línea única, y una rotación alrededor de este eje por un ángulo θ tiene valores propios λ = 1, e ^iθ , e ^{− iθ} . En el 4-espacio n = 4 , los cuatro valores propios son de la forma e ^{± iθ} , e ^{± iφ} . La rotación nula tiene θ = φ = 0 . El caso de θ = 0, φ ≠ 0 se denomina rotación simple , con dos valores propios unitarios que forman un plano de eje , y una rotación bidimensional ortogonal al plano de eje. De lo contrario, no hay plano de eje. El caso de θ = φ se denomina rotación isoclínica , que tiene valores propios e ^{± iθ} repetidos dos veces, por lo que cada vector rota un ángulo θ .

La traza de una matriz de rotación es igual a la suma de sus valores propios. Para n = 2 , una rotación en un ángulo θ tiene una traza 2 cos θ . Para n = 3 , una rotación alrededor de cualquier eje en un ángulo θ tiene una traza 1 + 2 cos θ . Para n = 4 , la traza es 2(cos θ + cos φ ) , que se convierte en 4 cos θ para una rotación isoclínica.

En geometría euclidiana , una rotación es un ejemplo de isometría , una transformación que mueve puntos sin cambiar las distancias entre ellos. Las rotaciones se distinguen de otras isometrías por dos propiedades adicionales: dejan (al menos) un punto fijo y dejan la " lateralidad " sin cambios. Por el contrario, una traslación mueve todos los puntos, una reflexión intercambia el orden hacia la izquierda y hacia la derecha, una reflexión de deslizamiento hace ambas cosas y una rotación impropia combina un cambio en la lateralidad con una rotación normal.

Si se toma un punto fijo como origen de un sistema de coordenadas cartesianas , entonces a cada punto se le pueden dar coordenadas como un desplazamiento desde el origen. De este modo, se puede trabajar con el espacio vectorial de desplazamientos en lugar de con los puntos mismos. Ahora supongamos que ( p ₁ , ..., p _n ) son las coordenadas del vector p desde el origen O hasta el punto P . Elijamos una base ortonormal para nuestras coordenadas; entonces, la distancia al cuadrado a P , según Pitágoras , es

${\displaystyle d^{2}(O,P)=\|\mathbf {p} \|^{2}=\sum _{r=1}^{n}p_{r}^{2}}$

que se puede calcular mediante la multiplicación de matrices

${\displaystyle \|\mathbf {p} \|^{2}={\begin{bmatrix}p_{1}\cdots p_{n}\end{bmatrix}}{\begin{bmatrix}p_{1}\\\vdots \\p_{n}\end{bmatrix}}=\mathbf {p} ^{\mathsf {T}}\mathbf {p} .}$

Una rotación geométrica transforma las líneas en líneas y conserva las razones de las distancias entre los puntos. A partir de estas propiedades se puede demostrar que una rotación es una transformación lineal de los vectores y, por lo tanto, se puede escribir en forma matricial , Q p . El hecho de que una rotación conserve, no solo las razones, sino también las distancias mismas, se enuncia como

${\displaystyle \mathbf {p} ^{\mathsf {T}}\mathbf {p} =(Q\mathbf {p} )^{\mathsf {T}}(Q\mathbf {p} ),}$

o

${\displaystyle {\begin{aligned}\mathbf {p} ^{\mathsf {T}}I\mathbf {p} &{}=\left(\mathbf {p} ^{\mathsf {T}}Q^{\mathsf {T}}\right)(Q\mathbf {p} )\\&{}=\mathbf {p} ^{\mathsf {T}}\left(Q^{\mathsf {T}}Q\right)\mathbf {p} .\end{aligned}}}$

Como esta ecuación es válida para todos los vectores, p , se concluye que cada matriz de rotación, Q , satisface la condición de ortogonalidad ,

${\displaystyle Q^{\mathsf {T}}Q=I.}$

Las rotaciones preservan la lateralidad porque no pueden cambiar el orden de los ejes, lo que implica la condición especial de la matriz ,

${\displaystyle \det Q=+1.}$

Igualmente importante es que se puede demostrar que cualquier matriz que satisfaga estas dos condiciones actúa como una rotación.

La inversa de una matriz de rotación es su transpuesta, que también es una matriz de rotación:

${\displaystyle {\begin{aligned}\left(Q^{\mathsf {T}}\right)^{\mathsf {T}}\left(Q^{\mathsf {T}}\right)&=QQ^{\mathsf {T}}=I\\\det Q^{\mathsf {T}}&=\det Q=+1.\end{aligned}}}$

El producto de dos matrices de rotación es una matriz de rotación:

${\displaystyle {\begin{aligned}\left(Q_{1}Q_{2}\right)^{\mathsf {T}}\left(Q_{1}Q_{2}\right)&=Q_{2}^{\mathsf {T}}\left(Q_{1}^{\mathsf {T}}Q_{1}\right)Q_{2}=I\\\det \left(Q_{1}Q_{2}\right)&=\left(\det Q_{1}\right)\left(\det Q_{2}\right)=+1.\end{aligned}}}$

Para n > 2 , la multiplicación de matrices de rotación n × n generalmente no es conmutativa .

${\displaystyle {\begin{aligned}Q_{1}&={\begin{bmatrix}0&-1&0\\1&0&0\\0&0&1\end{bmatrix}}&Q_{2}&={\begin{bmatrix}0&0&1\\0&1&0\\-1&0&0\end{bmatrix}}\\Q_{1}Q_{2}&={\begin{bmatrix}0&-1&0\\0&0&1\\-1&0&0\end{bmatrix}}&Q_{2}Q_{1}&={\begin{bmatrix}0&0&1\\1&0&0\\0&1&0\end{bmatrix}}.\end{aligned}}}$

Observando que cualquier matriz identidad es una matriz de rotación, y que la multiplicación de matrices es asociativa , podemos resumir todas estas propiedades diciendo que las matrices de rotación n × n forman un grupo , que para n > 2 es no abeliano , llamado grupo ortogonal especial , y denotado por SO( n ) , SO( n , R ) , SO _n o SO _n ( R ) , el grupo de matrices de rotación n × n es isomorfo al grupo de rotaciones en un espacio n -dimensional . Esto significa que la multiplicación de matrices de rotación corresponde a la composición de rotaciones, aplicada en orden de izquierda a derecha de sus matrices correspondientes.

La interpretación de una matriz de rotación puede estar sujeta a muchas ambigüedades.

En la mayoría de los casos el efecto de la ambigüedad es equivalente al efecto de una inversión de la matriz de rotación (para estas matrices ortogonales es equivalente la matriz transpuesta ).

Transformación de alias o coartada (pasiva o activa)

Las coordenadas de un punto P pueden cambiar debido a una rotación del sistema de coordenadas CS ( alias ), o una rotación del punto P ( alibi ). En este último caso, la rotación de P también produce una rotación del vector v que representa a P. En otras palabras, o bien P y v son fijos mientras CS rota (alias), o bien CS es fijo mientras P y v rotan (alibi). Cualquier rotación dada puede describirse legítimamente de ambas formas, ya que los vectores y los sistemas de coordenadas en realidad rotan entre sí, alrededor del mismo eje pero en direcciones opuestas. A lo largo de este artículo, elegimos el enfoque alibi para describir las rotaciones. Por ejemplo,

${\displaystyle R(\theta )={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}}$

representa una rotación en sentido antihorario de un vector v en un ángulo θ , o una rotación de CS en el mismo ángulo pero en la dirección opuesta (es decir, en el sentido de las agujas del reloj). Las transformaciones de coartada y alias también se conocen como transformaciones activas y pasivas , respectivamente.

Pre-multiplicación o post-multiplicación

El mismo punto P puede representarse mediante un vector columna v o un vector fila w . Las matrices de rotación pueden premultiplicar los vectores columna ( R v ), o posmultiplicar los vectores fila ( w R ). Sin embargo, R v produce una rotación en la dirección opuesta con respecto a w R . A lo largo de este artículo, las rotaciones producidas en vectores columna se describen mediante una premultiplicación. Para obtener exactamente la misma rotación (es decir, las mismas coordenadas finales del punto P ), el vector fila equivalente debe posmultiplicarse por la transpuesta de R (es decir, w R ^T ).

Coordenadas para diestros o zurdos

La matriz y el vector se pueden representar con respecto a un sistema de coordenadas dextrógiro o levógiro. A lo largo del artículo, asumimos una orientación dextrógira, a menos que se especifique lo contrario.

Vectores o formas

El espacio vectorial tiene un espacio dual de formas lineales , y la matriz puede actuar sobre vectores o formas.

Considere la matriz de rotación 3 × 3

${\displaystyle Q={\begin{bmatrix}0.36&0.48&-0.80\\-0.80&0.60&0.00\\0.48&0.64&0.60\end{bmatrix}}.}$

Si Q actúa en una determinada dirección, v , puramente como una escala por un factor λ , entonces tenemos

${\displaystyle Q\mathbf {v} =\lambda \mathbf {v} ,}$

de modo que

${\displaystyle \mathbf {0} =(\lambda I-Q)\mathbf {v} .}$

Por lo tanto, λ es una raíz del polinomio característico de Q ,

${\displaystyle {\begin{aligned}0&{}=\det(\lambda I-Q)\\&{}=\lambda ^{3}-{\tfrac {39}{25}}\lambda ^{2}+{\tfrac {39}{25}}\lambda -1\\&{}=(\lambda -1)\left(\lambda ^{2}-{\tfrac {14}{25}}\lambda +1\right).\end{aligned}}}$

Dos características son dignas de mención. Primero, una de las raíces (o valores propios ) es 1, lo que nos dice que alguna dirección no se ve afectada por la matriz. Para rotaciones en tres dimensiones, este es el eje de la rotación (un concepto que no tiene significado en ninguna otra dimensión). Segundo, las otras dos raíces son un par de conjugados complejos, cuyo producto es 1 (el término constante de la cuadrática), y cuya suma es 2 cos θ (el término lineal negado). Esta factorización es de interés para matrices de rotación 3 × 3 porque ocurre lo mismo para todas ellas. (Como casos especiales, para una rotación nula los "conjugados complejos" son ambos 1, y para una rotación de 180° son ambos −1.) Además, una factorización similar se cumple para cualquier matriz de rotación n × n . Si la dimensión, n , es impar, habrá un valor propio "colgando" de 1; y para cualquier dimensión el resto de los factores polinomiales en términos cuadráticos como el de aquí (con los dos casos especiales anotados). Tenemos la garantía de que el polinomio característico tendrá grado n y por lo tanto n valores propios. Y como una matriz de rotación conmuta con su transpuesta, es una matriz normal , por lo que se puede diagonalizar. Concluimos que toda matriz de rotación, cuando se expresa en un sistema de coordenadas adecuado, se divide en rotaciones independientes de subespacios bidimensionales, como máximo ⁠norte/2⁠ de ellos.

La suma de las entradas en la diagonal principal de una matriz se llama traza ; no cambia si reorientamos el sistema de coordenadas, y siempre es igual a la suma de los valores propios. Esto tiene la implicación conveniente para las matrices de rotación 2 × 2 y 3 × 3 de que la traza revela el ángulo de rotación , θ , en el espacio bidimensional (o subespacio). Para una matriz 2 × 2 la traza es 2 cos θ , y para una matriz 3 × 3 es 1 + 2 cos θ . En el caso tridimensional, el subespacio consiste en todos los vectores perpendiculares al eje de rotación (la dirección invariante, con valor propio 1). Por lo tanto, podemos extraer de cualquier matriz de rotación 3 × 3 un eje de rotación y un ángulo, y estos determinan completamente la rotación.

Las restricciones de una matriz de rotación 2 × 2 implican que debe tener la forma

${\displaystyle Q={\begin{bmatrix}a&-b\\b&a\end{bmatrix}}}$

con a ² + b ² = 1 . Por lo tanto, podemos establecer a = cos θ y b = sen θ , para algún ángulo θ . Para resolver θ no es suficiente observar a solo o b solo; debemos considerar ambos juntos para colocar el ángulo en el cuadrante correcto , utilizando una función arcotangente de dos argumentos .

Ahora consideremos la primera columna de una matriz de rotación de 3 × 3 ,

${\displaystyle {\begin{bmatrix}a\\b\\c\end{bmatrix}}.}$

Aunque a ² + b ² probablemente no será igual a 1, sino algún valor r ² < 1 , podemos usar una ligera variación del cálculo anterior para encontrar una llamada rotación de Givens que transforma la columna a

${\displaystyle {\begin{bmatrix}r\\0\\c\end{bmatrix}},}$

Poniendo a cero b . Esto actúa sobre el subespacio abarcado por los ejes x e y . Podemos repetir el proceso para el subespacio xz hasta poner a cero c . Al actuar sobre la matriz completa, estas dos rotaciones producen la forma esquemática

${\displaystyle Q_{xz}Q_{xy}Q={\begin{bmatrix}1&0&0\\0&\ast &\ast \\0&\ast &\ast \end{bmatrix}}.}$

Si nos centramos en la segunda columna, una rotación de Givens del subespacio yz puede ahora poner a cero el valor z . Esto hace que la matriz completa adopte la forma

${\displaystyle Q_{yz}Q_{xz}Q_{xy}Q={\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}},}$

que es una matriz identidad. Por lo tanto, hemos descompuesto Q como

${\displaystyle Q=Q_{xy}^{-1}Q_{xz}^{-1}Q_{yz}^{-1}.}$

Una matriz de rotación n × n tendrá ( n − 1) + ( n − 2) + ⋯ + 2 + 1 , o

${\displaystyle \sum _{k=1}^{n-1}k={\frac {1}{2}}n(n-1)}$

entradas debajo de la diagonal a cero. Podemos ponerlas a cero extendiendo la misma idea de recorrer las columnas con una serie de rotaciones en una secuencia fija de planos. Concluimos que el conjunto de matrices de rotación n × n , cada una de las cuales tiene n ² entradas, se puede parametrizar mediante ⁠1/2⁠ n ( n − 1) ángulos.

En tres dimensiones, esto replantea en forma matricial una observación hecha por Euler , por lo que los matemáticos llaman a la secuencia ordenada de tres ángulos ángulos de Euler . Sin embargo, la situación es algo más complicada de lo que hemos indicado hasta ahora. A pesar de la pequeña dimensión, en realidad tenemos una libertad considerable en la secuencia de pares de ejes que usamos; y también tenemos cierta libertad en la elección de los ángulos. Por lo tanto, encontramos muchas convenciones diferentes empleadas cuando se parametrizan rotaciones tridimensionales para física, o medicina, o química, u otras disciplinas. Cuando incluimos la opción de ejes del mundo o ejes del cuerpo, son posibles 24 secuencias diferentes. Y mientras que algunas disciplinas llaman a cualquier secuencia ángulos de Euler, otras dan nombres diferentes (Cardano, Tait–Bryan, balanceo-cabeceo-guiñada ) a diferentes secuencias.

Una razón para la gran cantidad de opciones es que, como se señaló anteriormente, las rotaciones en tres dimensiones (y superiores) no conmutan. Si invertimos una secuencia dada de rotaciones, obtenemos un resultado diferente. Esto también implica que no podemos componer dos rotaciones sumando sus ángulos correspondientes. Por lo tanto, los ángulos de Euler no son vectores , a pesar de una similitud en apariencia como un triplete de números.

Una matriz de rotación de 3 × 3 como

${\displaystyle Q_{3\times 3}={\begin{bmatrix}\cos \theta &-\sin \theta &{\color {CadetBlue}0}\\\sin \theta &\cos \theta &{\color {CadetBlue}0}\\{\color {CadetBlue}0}&{\color {CadetBlue}0}&{\color {CadetBlue}1}\end{bmatrix}}}$

sugiere una matriz de rotación de 2 × 2 ,

${\displaystyle Q_{2\times 2}={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}},}$

Está incrustado en la esquina superior izquierda:

${\displaystyle Q_{3\times 3}=\left[{\begin{matrix}Q_{2\times 2}&\mathbf {0} \\\mathbf {0} ^{\mathsf {T}}&1\end{matrix}}\right].}$

Esto no es una ilusión; no sólo una, sino muchas copias de rotaciones n -dimensionales se encuentran dentro de rotaciones ( n + 1) -dimensionales, como subgrupos . Cada incrustación deja una dirección fija, que en el caso de matrices 3 × 3 es el eje de rotación. Por ejemplo, tenemos

${\displaystyle {\begin{aligned}Q_{\mathbf {x} }(\theta )&={\begin{bmatrix}{\color {CadetBlue}1}&{\color {CadetBlue}0}&{\color {CadetBlue}0}\\{\color {CadetBlue}0}&\cos \theta &-\sin \theta \\{\color {CadetBlue}0}&\sin \theta &\cos \theta \end{bmatrix}},\\[8px]Q_{\mathbf {y} }(\theta )&={\begin{bmatrix}\cos \theta &{\color {CadetBlue}0}&\sin \theta \\{\color {CadetBlue}0}&{\color {CadetBlue}1}&{\color {CadetBlue}0}\\-\sin \theta &{\color {CadetBlue}0}&\cos \theta \end{bmatrix}},\\[8px]Q_{\mathbf {z} }(\theta )&={\begin{bmatrix}\cos \theta &-\sin \theta &{\color {CadetBlue}0}\\\sin \theta &\cos \theta &{\color {CadetBlue}0}\\{\color {CadetBlue}0}&{\color {CadetBlue}0}&{\color {CadetBlue}1}\end{bmatrix}},\end{aligned}}}$

fijando el eje x , el eje y y el eje z , respectivamente. El eje de rotación no necesita ser un eje de coordenadas; si u = ( x , y , z ) es un vector unitario en la dirección deseada, entonces

${\displaystyle {\begin{aligned}Q_{\mathbf {u} }(\theta )&={\begin{bmatrix}0&-z&y\\z&0&-x\\-y&x&0\end{bmatrix}}\sin \theta +\left(I-\mathbf {u} \mathbf {u} ^{\mathsf {T}}\right)\cos \theta +\mathbf {u} \mathbf {u} ^{\mathsf {T}}\\[8px]&={\begin{bmatrix}\left(1-x^{2}\right)c_{\theta }+x^{2}&-zs_{\theta }-xyc_{\theta }+xy&ys_{\theta }-xzc_{\theta }+xz\\zs_{\theta }-xyc_{\theta }+xy&\left(1-y^{2}\right)c_{\theta }+y^{2}&-xs_{\theta }-yzc_{\theta }+yz\\-ys_{\theta }-xzc_{\theta }+xz&xs_{\theta }-yzc_{\theta }+yz&\left(1-z^{2}\right)c_{\theta }+z^{2}\end{bmatrix}}\\[8px]&={\begin{bmatrix}x^{2}(1-c_{\theta })+c_{\theta }&xy(1-c_{\theta })-zs_{\theta }&xz(1-c_{\theta })+ys_{\theta }\\xy(1-c_{\theta })+zs_{\theta }&y^{2}(1-c_{\theta })+c_{\theta }&yz(1-c_{\theta })-xs_{\theta }\\xz(1-c_{\theta })-ys_{\theta }&yz(1-c_{\theta })+xs_{\theta }&z^{2}(1-c_{\theta })+c_{\theta }\end{bmatrix}},\end{aligned}}}$

donde c _θ = cos θ , s _θ = sin θ , es una rotación de ángulo θ dejando fijo el eje u .

Una dirección en un espacio de dimensión ( n + 1) será un vector de magnitud unitaria, que podemos considerar un punto en una esfera generalizada, S ⁿ . Por lo tanto, es natural describir el grupo de rotación SO( n + 1) como una combinación de SO( n ) y S ⁿ . Un formalismo adecuado es el fibrado ,

${\displaystyle SO(n)\hookrightarrow SO(n+1)\to S^{n},}$

donde para cada dirección en el espacio base, S ⁿ , la fibra sobre ella en el espacio total, SO( n + 1) , es una copia del espacio de la fibra, SO( n ) , es decir, las rotaciones que mantienen fija esa dirección.

Así, podemos construir una matriz de rotación n × n comenzando con una matriz 2 × 2 , apuntando su eje fijo a S ² (la esfera ordinaria en el espacio tridimensional), apuntando la rotación resultante a S ³ , y así sucesivamente hasta S ^{n −1} . Se puede seleccionar un punto en S ⁿ usando n números, por lo que nuevamente tenemos ⁠1/2⁠ n ( n − 1) números para describir cualquiermatriz de rotación n × n .

De hecho, podemos considerar la descomposición angular secuencial, analizada previamente, como una inversión de este proceso. La composición de n − 1 rotaciones de Givens lleva la primera columna (y fila) a (1, 0, ..., 0) , de modo que el resto de la matriz es una matriz de rotación de dimensión uno menos, incrustada de modo que (1, 0, ..., 0) quede fija.

Cuando una matriz de rotación n × n Q , no incluye un valor propio −1, por lo que ninguna de las rotaciones planares que comprende son rotaciones de 180°, entonces Q + I es una matriz invertible . La mayoría de las matrices de rotación se ajustan a esta descripción, y para ellas se puede demostrar que ( Q − I )( Q + I ) ⁻¹ es una matriz antisimétrica , A . Por lo tanto A ^T = − A ; y dado que la diagonal es necesariamente cero, y dado que el triángulo superior determina el inferior, A contiene ⁠1/2⁠ n ( n − 1) números independientes.

Convenientemente, I − A es invertible siempre que A sea antisimétrico; por lo tanto, podemos recuperar la matriz original utilizando la transformada de Cayley ,

${\displaystyle A\mapsto (I+A)(I-A)^{-1},}$

que convierte cualquier matriz A antisimétrica en una matriz de rotación. De hecho, aparte de las excepciones señaladas, podemos producir cualquier matriz de rotación de esta manera. Aunque en aplicaciones prácticas difícilmente podemos permitirnos ignorar las rotaciones de 180°, la transformada de Cayley sigue siendo una herramienta potencialmente útil, que proporciona una parametrización de la mayoría de las matrices de rotación sin funciones trigonométricas.

En tres dimensiones, por ejemplo, tenemos (Cayley 1846)

${\displaystyle {\begin{aligned}&{\begin{bmatrix}0&-z&y\\z&0&-x\\-y&x&0\end{bmatrix}}\mapsto \\[3pt]\quad {\frac {1}{1+x^{2}+y^{2}+z^{2}}}&{\begin{bmatrix}1+x^{2}-y^{2}-z^{2}&2xy-2z&2y+2xz\\2xy+2z&1-x^{2}+y^{2}-z^{2}&2yz-2x\\2xz-2y&2x+2yz&1-x^{2}-y^{2}+z^{2}\end{bmatrix}}.\end{aligned}}}$

Si condensamos las entradas oblicuas en un vector, ( x , y , z ) , entonces producimos una rotación de 90° alrededor del eje x para (1, 0, 0), alrededor del eje y para (0, 1, 0), y alrededor del eje z para (0, 0, 1). Las rotaciones de 180° están fuera de alcance; porque, en el límite cuando x → ∞ , ( x , 0, 0) se aproxima a una rotación de 180° alrededor del eje x , y de manera similar para otras direcciones.

Para el caso 2D, una matriz de rotación se puede descomponer en tres matrices de corte (Paeth 1986):

${\displaystyle {\begin{aligned}R(\theta )&{}={\begin{bmatrix}1&-\tan {\frac {\theta }{2}}\\0&1\end{bmatrix}}{\begin{bmatrix}1&0\\\sin \theta &1\end{bmatrix}}{\begin{bmatrix}1&-\tan {\frac {\theta }{2}}\\0&1\end{bmatrix}}\end{aligned}}}$

Esto es útil, por ejemplo, en gráficos de computadora, ya que las operaciones de corte se pueden implementar con menos instrucciones de multiplicación que rotando un mapa de bits directamente. En las computadoras modernas, esto puede no tener importancia, pero puede ser relevante para microprocesadores muy antiguos o de gama baja.

Una rotación también puede escribirse como dos cortes y escalas (Daubechies y Sweldens 1998):

${\displaystyle {\begin{aligned}R(\theta )&{}={\begin{bmatrix}1&0\\\tan \theta &1\end{bmatrix}}{\begin{bmatrix}1&-\sin \theta \cos \theta \\0&1\end{bmatrix}}{\begin{bmatrix}\cos \theta &0\\0&{\frac {1}{\cos \theta }}\end{bmatrix}}\end{aligned}}}$

A continuación se presentan algunos datos básicos sobre el papel de la colección de todas las matrices de rotación de una dimensión fija (aquí principalmente 3) en matemáticas y particularmente en física donde la simetría rotacional es un requisito de cada ley verdaderamente fundamental (debido al supuesto de isotropía del espacio ), y donde la misma simetría, cuando está presente, es una propiedad simplificadora de muchos problemas de naturaleza menos fundamental. Los ejemplos abundan en la mecánica clásica y la mecánica cuántica . El conocimiento de la parte de las soluciones perteneciente a esta simetría se aplica (con salvedades) a todos esos problemas y se puede factorizar de un problema específico en cuestión, reduciendo así su complejidad. Un excelente ejemplo, en matemáticas y física, sería la teoría de los armónicos esféricos . Su papel en la teoría de grupos de los grupos de rotación es el de ser un espacio de representación para todo el conjunto de representaciones irreducibles de dimensión finita del grupo de rotación SO(3). Para este tema, consulte Grupo de rotación SO(3) § Armónicos esféricos .

Para obtener más detalles se hace referencia a los artículos principales enumerados en cada subsección.

Las matrices de rotación n × n para cada n forman un grupo , el grupo ortogonal especial , SO( n ) . Esta estructura algebraica está acoplada con una estructura topológica heredada de de tal manera que las operaciones de multiplicación y toma de la inversa son funciones analíticas de las entradas de la matriz. Por lo tanto, SO( n ) es para cada n un grupo de Lie . Es compacto y conexo , pero no simplemente conexo . También es un grupo semisimple , de hecho un grupo simple con la excepción de SO(4). ^[12] La relevancia de esto es que todos los teoremas y toda la maquinaria de la teoría de variedades analíticas (las variedades analíticas son en particular variedades suaves ) se aplican y la teoría de representación bien desarrollada de grupos semisimples compactos está lista para su uso.${\displaystyle \operatorname {GL} _{n}(\mathbb {R} )}$

El álgebra de Lie so ( n ) de SO( n ) está dada por

${\displaystyle {\mathfrak {so}}(n)={\mathfrak {o}}(n)=\left\{X\in M_{n}(\mathbb {R} )\mid X=-X^{\mathsf {T}}\right\},}$

y es el espacio de matrices antisimétricas de dimensión n , véase grupo clásico , donde o ( n ) es el álgebra de Lie de O( n ) , el grupo ortogonal . Como referencia, la base más común para ( 3) es

${\displaystyle L_{\mathbf {x} }={\begin{bmatrix}0&0&0\\0&0&-1\\0&1&0\end{bmatrix}},\quad L_{\mathbf {y} }={\begin{bmatrix}0&0&1\\0&0&0\\-1&0&0\end{bmatrix}},\quad L_{\mathbf {z} }={\begin{bmatrix}0&-1&0\\1&0&0\\0&0&0\end{bmatrix}}.}$

La conexión del álgebra de Lie con el grupo de Lie es el mapa exponencial , que se define utilizando la serie exponencial matricial estándar para e ^{A [13]} Para cualquier matriz antisimétrica A , exp( A ) es siempre una matriz de rotación. ^{[nb 3]}

Un ejemplo práctico importante es el caso 3 × 3. En el grupo de rotación SO(3) , se muestra que se puede identificar cada A ∈ so (3) con un vector de Euler ω = θ u , donde u = ( x , y , z ) es un vector de magnitud unitaria.

Por las propiedades de la identificación , u está en el espacio nulo de A. Por lo tanto, u queda invariante por exp( A ) y, por lo tanto, es un eje de rotación.${\displaystyle \mathbf {su} (2)\cong \mathbb {R} ^{3}}$

Según la fórmula de rotación de Rodrigues en forma matricial , se obtiene,

${\displaystyle {\begin{aligned}\exp(A)&=\exp {\bigl (}\theta (\mathbf {u} \cdot \mathbf {L} ){\bigr )}\\&=\exp \left({\begin{bmatrix}0&-z\theta &y\theta \\z\theta &0&-x\theta \\-y\theta &x\theta &0\end{bmatrix}}\right)\\&=I+\sin \theta \ \mathbf {u} \cdot \mathbf {L} +(1-\cos \theta )(\mathbf {u} \cdot \mathbf {L} )^{2},\end{aligned}}}$

dónde

${\displaystyle \mathbf {u} \cdot \mathbf {L} ={\begin{bmatrix}0&-z&y\\z&0&-x\\-y&x&0\end{bmatrix}}.}$

Esta es la matriz para una rotación alrededor del eje u con un ángulo θ . Para obtener más detalles, consulte el mapa exponencial SO(3) .

La fórmula BCH proporciona una expresión explícita para Z = log( e ^X e ^Y ) en términos de una expansión en serie de conmutadores anidados de X e Y . ^[14] Esta expansión general se desarrolla como ^{[nb 4]}

${\displaystyle Z=C(X,Y)=X+Y+{\tfrac {1}{2}}[X,Y]+{\tfrac {1}{12}}{\bigl [}X,[X,Y]{\bigr ]}-{\tfrac {1}{12}}{\bigl [}Y,[X,Y]{\bigr ]}+\cdots .}$

En el caso 3 × 3 , la expansión infinita general tiene una forma compacta, ^[15]

${\displaystyle Z=\alpha X+\beta Y+\gamma [X,Y],}$

para coeficientes de funciones trigonométricas adecuados, detallados en la fórmula de Baker–Campbell–Hausdorff para SO(3) .

Como identidad de grupo, lo anterior se cumple para todas las representaciones fieles , incluido el doblete (representación de espinor), que es más simple. La misma fórmula explícita se deduce directamente a través de las matrices de Pauli; véase la derivación 2 × 2 para SU(2) . Para el caso general n × n , se podría utilizar la Ref. ^[16]

El grupo de Lie de matrices de rotación n × n , SO( n ) , no está simplemente conexo , por lo que la teoría de Lie nos dice que es una imagen homomórfica de un grupo de recubrimiento universal . A menudo, el grupo de recubrimiento, que en este caso se denomina grupo de espín denotado por Spin( n ) , es más simple y más natural para trabajar. ^[17]

En el caso de rotaciones planares, SO(2) es topológicamente un círculo , S ¹ . Su grupo de recubrimiento universal, Spin(2), es isomorfo a la línea real , R , bajo la adición. Siempre que se utilizan ángulos de magnitud arbitraria, se aprovecha la conveniencia del recubrimiento universal. Cada matriz de rotación 2 × 2 se produce por una infinidad contable de ángulos, separados por múltiplos enteros de 2 π . En consecuencia, el grupo fundamental de SO(2) es isomorfo a los números enteros, Z .

En el caso de rotaciones espaciales, SO(3) es topológicamente equivalente al espacio proyectivo real tridimensional , RP ³ . Su grupo de recubrimiento universal, Spin(3), es isomorfo a la 3-esfera , S ³ . Toda matriz de rotación 3 × 3 se produce por dos puntos opuestos en la esfera. En consecuencia, el grupo fundamental de SO(3) es isomorfo al grupo de dos elementos, Z ₂ .

También podemos describir Spin(3) como isomorfo a los cuaterniones de norma unitaria bajo multiplicación, o a ciertas matrices reales de 4 × 4 , o a matrices unitarias especiales complejas de 2 × 2 , a saber, SU(2). Las funciones de recubrimiento para el primer y el último caso se dan por

${\displaystyle \mathbb {H} \supset \{q\in \mathbb {H} :\|q\|=1\}\ni w+\mathbf {i} x+\mathbf {j} y+\mathbf {k} z\mapsto {\begin{bmatrix}1-2y^{2}-2z^{2}&2xy-2zw&2xz+2yw\\2xy+2zw&1-2x^{2}-2z^{2}&2yz-2xw\\2xz-2yw&2yz+2xw&1-2x^{2}-2y^{2}\end{bmatrix}}\in \mathrm {SO} (3),}$

y

${\displaystyle \mathrm {SU} (2)\ni {\begin{bmatrix}\alpha &\beta \\-{\overline {\beta }}&{\overline {\alpha }}\end{bmatrix}}\mapsto {\begin{bmatrix}{\frac {1}{2}}\left(\alpha ^{2}-\beta ^{2}+{\overline {\alpha ^{2}}}-{\overline {\beta ^{2}}}\right)&{\frac {i}{2}}\left(-\alpha ^{2}-\beta ^{2}+{\overline {\alpha ^{2}}}+{\overline {\beta ^{2}}}\right)&-\alpha \beta -{\overline {\alpha }}{\overline {\beta }}\\{\frac {i}{2}}\left(\alpha ^{2}-\beta ^{2}-{\overline {\alpha ^{2}}}+{\overline {\beta ^{2}}}\right)&{\frac {i}{2}}\left(\alpha ^{2}+\beta ^{2}+{\overline {\alpha ^{2}}}+{\overline {\beta ^{2}}}\right)&-i\left(+\alpha \beta -{\overline {\alpha }}{\overline {\beta }}\right)\\\alpha {\overline {\beta }}+{\overline {\alpha }}\beta &i\left(-\alpha {\overline {\beta }}+{\overline {\alpha }}\beta \right)&\alpha {\overline {\alpha }}-\beta {\overline {\beta }}\end{bmatrix}}\in \mathrm {SO} (3).}$