Número de Mach
El número de Mach (M o Ma), a menudo solo Mach, (/mɑːk / ; alemán : [ max ] ) es una cantidad adimensional en dinámica de fluidos que representa la relación entre la velocidad del flujo más allá de un límite y la velocidad local del sonido . [1] [2] Lleva el nombre del físico y filósofo austríaco Ernst Mach .
dónde:
- M es el número de Mach local,
- u es la velocidad del flujo local con respecto a los límites (ya sean internos, como un objeto inmerso en el flujo, o externos, como un canal), y
- c es la velocidad del sonido en el medio, que en el aire varía con la raíz cuadrada de la temperatura termodinámica .
Por definición, a Mach 1, la velocidad de flujo local u es igual a la velocidad del sonido. A Mach 0,65, u es el 65 % de la velocidad del sonido (subsónica) y, a Mach 1,35, u es un 35 % más rápida que la velocidad del sonido (supersónica). Los pilotos de vehículos aeroespaciales de gran altitud utilizan el número de Mach de vuelo para expresar la velocidad aerodinámica real de un vehículo , pero el campo de flujo alrededor de un vehículo varía en tres dimensiones, con variaciones correspondientes en el número de Mach local.
.jpg/440px-FA-18_Hornet_breaking_sound_barrier_(7_July_1999).jpg)
La velocidad local del sonido, y por lo tanto el número de Mach, depende de la temperatura del gas circundante. El número de Mach se utiliza principalmente para determinar la aproximación con la que un flujo puede ser tratado como un flujo incompresible . El medio puede ser un gas o un líquido. El límite puede estar viajando en el medio, o puede estar estacionario mientras el medio fluye a lo largo de él, o ambos pueden estar en movimiento, con diferentes velocidades : lo que importa es su velocidad relativa con respecto al otro. El límite puede ser el límite de un objeto inmerso en el medio, o de un canal como una boquilla , un difusor o un túnel de viento que canalice el medio. Como el número de Mach se define como la relación de dos velocidades, es una cantidad adimensional. Si M < 0,2–0,3 y el flujo es casi constante e isotérmico , los efectos de compresibilidad serán pequeños y se pueden utilizar ecuaciones de flujo incompresible simplificadas. [1] [2]
Etimología
El número de Mach debe su nombre al físico y filósofo Ernst Mach [3] según una propuesta del ingeniero aeronáutico Jakob Ackeret en 1929. [4] La palabra Mach siempre se escribe con mayúscula, ya que deriva de un nombre propio, y dado que el número de Mach es una cantidad adimensional en lugar de una unidad de medida , el número viene después de la palabra Mach; el segundo número de Mach es Mach 2 en lugar de 2 Mach (o Machs). Esto recuerda un poco a la marca de unidad de sondeo oceánico moderna temprana (un sinónimo de braza ), que también era la primera unidad, y puede haber influido en el uso del término Mach. En la década anterior al vuelo humano más rápido que el sonido , los ingenieros aeronáuticos se referían a la velocidad del sonido como el número de Mach , nunca Mach 1. [ 5]
Descripción general

El número de Mach es una medida de las características de compresibilidad del flujo de fluido : el fluido (aire) se comporta bajo la influencia de la compresibilidad de manera similar a un número de Mach dado, independientemente de otras variables. [6] Como se modela en la Atmósfera Estándar Internacional , aire seco al nivel medio del mar , temperatura estándar de 15 °C (59 °F), la velocidad del sonido es de 340,3 metros por segundo (1116,5 pies/s; 761,23 mph; 1225,1 km/h; 661,49 kn). [7] La velocidad del sonido no es una constante; en un gas, aumenta proporcionalmente a la raíz cuadrada de la temperatura absoluta , y dado que la temperatura atmosférica generalmente disminuye con el aumento de la altitud entre el nivel del mar y los 11 000 metros (36 089 pies), la velocidad del sonido también disminuye. Por ejemplo, el modelo atmosférico estándar reduce la temperatura a -56,5 °C (-69,7 °F) a 11.000 metros (36.089 pies) de altitud, con una velocidad del sonido (Mach 1) correspondiente de 295,0 metros por segundo (967,8 pies/s; 659,9 mph; 1.062 km/h; 573,4 kn), el 86,7% del valor del nivel del mar.
Apariencia en la ecuación de continuidad
Como medida de la compresibilidad del flujo, el número de Mach se puede derivar de una escala apropiada de la ecuación de continuidad . [8] La ecuación de continuidad completa para un flujo de fluido general es: donde es la derivada del material , es la densidad y es la velocidad del flujo . Para cambios de densidad inducidos por presión isentrópica , donde es la velocidad del sonido. Luego, la ecuación de continuidad se puede modificar ligeramente para tener en cuenta esta relación: El siguiente paso es no dimensionalizar las variables como tales: donde es la escala de longitud característica, es la escala de velocidad característica, es la presión de referencia y es la densidad de referencia. Luego, la forma no dimensionalizada de la ecuación de continuidad se puede escribir como: donde el número de Mach . En el límite que , la ecuación de continuidad se reduce a — este es el requisito estándar para flujo incompresible .
Clasificación de los regímenes de Mach
Si bien los términos subsónico y supersónico , en el sentido más puro, se refieren a velocidades inferiores y superiores a la velocidad local del sonido respectivamente, los aerodinámicos suelen utilizar los mismos términos para hablar de rangos particulares de valores de Mach. Esto ocurre debido a la presencia de un régimen transónico alrededor del vuelo (corriente libre) M = 1 donde las aproximaciones de las ecuaciones de Navier-Stokes utilizadas para el diseño subsónico ya no se aplican; la explicación más simple es que el flujo alrededor de una estructura de avión comienza a superar localmente M = 1 aunque el número de Mach de corriente libre esté por debajo de este valor.
Mientras tanto, el régimen supersónico se utiliza generalmente para hablar del conjunto de números de Mach para los que se puede utilizar la teoría linealizada, donde, por ejemplo, el flujo ( de aire ) no reacciona químicamente y donde la transferencia de calor entre el aire y el vehículo se puede descuidar razonablemente en los cálculos.
En la siguiente tabla se hace referencia a los regímenes o rangos de valores de Mach , y no al significado puro de las palabras subsónico y supersónico .
En general, la NASA define hipersónico alto como cualquier número de Mach entre 10 y 25, y velocidad de reingreso como cualquier velocidad mayor que Mach 25. Las aeronaves que operan en este régimen incluyen el transbordador espacial y varios aviones espaciales en desarrollo.
| Régimen | Velocidad de vuelo | Características generales del plano | ||||
|---|---|---|---|---|---|---|
| (Mach) | (nudos) | (millas por hora) | (km/h) | (EM) | ||
| Subsónico | <0,8 | <530 | <609 | <980 | <273 | Generalmente se trata de aviones comerciales con turbofán y propulsados por hélice , con alas de alta relación de aspecto (delgadas) y características redondeadas como la nariz y los bordes de ataque. El rango de velocidad subsónica es el rango de velocidades dentro del cual todo el flujo de aire sobre una aeronave es menor que Mach 1. El número de Mach crítico (Mcrit) es el número de Mach de corriente libre más bajo en el que el flujo de aire sobre cualquier parte de la aeronave alcanza por primera vez Mach 1. Por lo tanto, el rango de velocidad subsónica incluye todas las velocidades que son menores que Mcrit. |
| Transónico | 0,8–1,2 | 530–794 | 609–914 | 980–1.470 | 273–409 | Los aviones transónicos casi siempre tienen alas en flecha , lo que provoca el retraso de la divergencia de arrastre, y a menudo presentan un diseño que se adhiere a los principios de la regla del área de Whitcomb . El rango de velocidad transónica es el rango de velocidades dentro del cual el flujo de aire sobre las diferentes partes de una aeronave se encuentra entre subsónico y supersónico. Por lo tanto, el régimen de vuelo desde Mcrit hasta Mach 1,3 se denomina rango transónico. |
| Supersónico | 1.2–5.0 | 794–3.308 | 915–3.806 | 1.470–6.126 | 410–1.702 | El rango de velocidad supersónica es el rango de velocidades dentro del cual todo el flujo de aire sobre una aeronave es supersónico (superior a Mach 1). Pero el flujo de aire que llega a los bordes de ataque se desacelera inicialmente, por lo que la velocidad de la corriente libre debe ser ligeramente superior a Mach 1 para garantizar que todo el flujo sobre la aeronave sea supersónico. Se acepta comúnmente que el rango de velocidad supersónica comienza con una velocidad de corriente libre superior a Mach 1,3. Las aeronaves diseñadas para volar a velocidades supersónicas muestran grandes diferencias en su diseño aerodinámico debido a las diferencias radicales en el comportamiento de los flujos por encima de Mach 1. Los bordes afilados, las secciones aerodinámicas delgadas y los estabilizadores laterales / alas móviles son comunes. Las aeronaves de combate modernas deben hacer concesiones para mantener el manejo a baja velocidad; los diseños supersónicos "verdaderos" incluyen el F-104 Starfighter , el MiG-31 , el North American XB-70 Valkyrie , el SR-71 Blackbird y el BAC/Aérospatiale Concorde . |
| Hipersónico | 5.0–10.0 | 3.308–6.615 | 3.806–7.680 | 6.126–12.251 | 1.702–3.403 | El X-15 , con una velocidad de Mach 6,72, es uno de los aviones tripulados más rápidos. Además, tiene una cubierta de níquel - titanio refrigerada ; está altamente integrado (debido al predominio de los efectos de interferencia: el comportamiento no lineal significa que la superposición de resultados para componentes separados no es válida) y tiene alas pequeñas, como las del X-51A Waverider , que alcanza Mach 5. |
| Altamente hipersónico | 10,0–25,0 | 6.615–16.537 | 7.680–19.031 | 12.251–30.626 | 3.403–8.508 | El X-43 de la NASA , con una velocidad de Mach 9,6, es uno de los aviones más rápidos. El control térmico se convierte en una consideración de diseño dominante. La estructura debe estar diseñada para funcionar en caliente o estar protegida por placas de silicato especiales o similares. El flujo que reacciona químicamente también puede provocar corrosión en la piel del vehículo, y el oxígeno atómico libre aparece en flujos de muy alta velocidad. Los diseños hipersónicos a menudo se ven obligados a adoptar configuraciones romas debido al aumento del calentamiento aerodinámico con un radio de curvatura reducido . |
| Velocidades de reingreso | >25.0 | >16.537 | >19.031 | >30,626 | >8,508 | Escudo térmico ablativo ; alas pequeñas o inexistentes; forma roma. Se afirma que el Avangard (vehículo de planeo hipersónico) ruso alcanza velocidades de Mach 27. |
Flujo de alta velocidad alrededor de objetos.
El vuelo se puede clasificar aproximadamente en seis categorías:
| Régimen | Subsónico | Transónico | Velocidad del sonido | Supersónico | Hipersónico | Hipervelocidad |
|---|---|---|---|---|---|---|
| Mach | <0,8 | 0,8–1,2 | 1.0 | 1.2–5.0 | 5.0–10.0 | >8.8 |
A modo de comparación: la velocidad requerida para una órbita terrestre baja es de aproximadamente 7,5 km/s = Mach 25,4 en el aire a grandes altitudes.
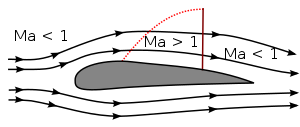
A velocidades transónicas, el campo de flujo alrededor del objeto incluye partes tanto subsónicas como supersónicas. El período transónico comienza cuando aparecen las primeras zonas de flujo M > 1 alrededor del objeto. En el caso de un perfil aerodinámico (como el ala de un avión), esto suele ocurrir por encima del ala. El flujo supersónico puede desacelerarse hasta alcanzar el nivel subsónico solo en un choque normal; esto suele ocurrir antes del borde de salida. (Fig. 1a)
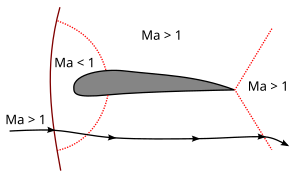
A medida que aumenta la velocidad, la zona de flujo M > 1 aumenta hacia los bordes de ataque y de salida. Cuando se alcanza y se supera M = 1, el choque normal alcanza el borde de salida y se convierte en un choque oblicuo débil: el flujo se desacelera sobre el choque, pero sigue siendo supersónico. Se crea un choque normal delante del objeto y la única zona subsónica en el campo de flujo es una pequeña área alrededor del borde de ataque del objeto. (Fig. 1b)
 |  |
| (a) | (b) |
Fig. 1. Número de Mach en el flujo de aire transónico alrededor de un perfil aerodinámico; M < 1 (a) y M > 1 (b).
Cuando un avión supera la velocidad de Mach 1 (es decir, la barrera del sonido ), se crea una gran diferencia de presión justo delante del avión . Esta diferencia de presión abrupta, llamada onda de choque , se propaga hacia atrás y hacia afuera del avión en forma de cono (el llamado cono de Mach ). Es esta onda de choque la que causa el estampido sónico que se escucha cuando un avión en movimiento rápido pasa por encima. Una persona dentro del avión no lo oirá. Cuanto mayor sea la velocidad, más estrecho será el cono; a poco más de M = 1, apenas es un cono, sino más bien un plano ligeramente cóncavo.
A una velocidad totalmente supersónica, la onda de choque comienza a tomar forma de cono y el flujo es completamente supersónico o (en el caso de un objeto contundente), solo queda una zona de flujo subsónico muy pequeña entre la punta del objeto y la onda de choque que crea delante de sí mismo. (En el caso de un objeto afilado, no hay aire entre la punta y la onda de choque: la onda de choque comienza desde la punta).
A medida que aumenta el número de Mach, también lo hace la fuerza de la onda de choque y el cono de Mach se vuelve cada vez más estrecho. A medida que el flujo de fluido cruza la onda de choque, su velocidad se reduce y la temperatura, la presión y la densidad aumentan. Cuanto más fuerte es el choque, mayores son los cambios. A números de Mach suficientemente altos, la temperatura aumenta tanto durante el choque que comienza la ionización y la disociación de las moléculas de gas detrás de la onda de choque. Estos flujos se denominan hipersónicos.
Está claro que cualquier objeto que viaje a velocidades hipersónicas también estará expuesto a las mismas temperaturas extremas que el gas detrás de la onda de choque de la nariz, y por lo tanto la elección de materiales resistentes al calor se vuelve importante.
Flujo de alta velocidad en un canal
Cuando el flujo en un canal se vuelve supersónico, se produce un cambio significativo. La conservación del caudal másico lleva a esperar que la contracción del canal de flujo aumente la velocidad del mismo (es decir, si se hace más estrecho el canal, el flujo de aire será más rápido) y a velocidades subsónicas esto es así. Sin embargo, una vez que el flujo se vuelve supersónico, la relación entre el área de flujo y la velocidad se invierte: la expansión del canal en realidad aumenta la velocidad.
El resultado obvio es que para acelerar un flujo hasta alcanzar velocidades supersónicas, se necesita una tobera convergente-divergente, donde la sección convergente acelera el flujo hasta alcanzar velocidades sónicas y la sección divergente continúa la aceleración. Estas toberas se denominan toberas de Laval y, en casos extremos, pueden alcanzar velocidades hipersónicas (Mach 13 [15.900 km/h; 9.900 mph] a 20 °C).
Un Machmeter de aeronave o sistema electrónico de información de vuelo ( EFIS ) puede mostrar el número de Mach derivado de la presión de estancamiento ( tubo de Pitot ) y la presión estática.
Cálculo
Cuando se conoce la velocidad del sonido, el número de Mach al que vuela un avión se puede calcular mediante
dónde:
- M es el número de Mach
- u es la velocidad de la aeronave en movimiento y
- c es la velocidad del sonido a la altitud dada (más apropiadamente, temperatura)
y la velocidad del sonido varía con la temperatura termodinámica como:
dónde:
- es la relación entre el calor específico de un gas a presión constante y el calor a un volumen constante (1,4 para el aire)
- es la constante de gas específica del aire.
- es la temperatura estática del aire.
Si no se conoce la velocidad del sonido, el número de Mach se puede determinar midiendo las distintas presiones del aire (estáticas y dinámicas) y utilizando la siguiente fórmula que se deriva de la ecuación de Bernoulli para números de Mach menores que 1.0. Suponiendo que el aire es un gas ideal , la fórmula para calcular el número de Mach en un flujo compresible subsónico es: [9]
dónde:
- q c es la presión de impacto (presión dinámica) y
- p es presión estática
- es la relación entre el calor específico de un gas a presión constante y el calor a un volumen constante (1,4 para el aire)
La fórmula para calcular el número de Mach en un flujo compresible supersónico se deriva de la ecuación de Pitot supersónica de Rayleigh :
Cálculo del número de Mach a partir de la presión del tubo de Pitot
El número de Mach es una función de la temperatura y la velocidad aerodinámica real. Sin embargo, los instrumentos de vuelo de las aeronaves funcionan utilizando la diferencia de presión para calcular el número de Mach, no la temperatura.
Suponiendo que el aire es un gas ideal , la fórmula para calcular el número de Mach en un flujo compresible subsónico se encuentra en la ecuación de Bernoulli para M < 1 (arriba): [9]
La fórmula para calcular el número de Mach en un flujo compresible supersónico se puede encontrar en la ecuación de Pitot supersónica de Rayleigh (arriba) usando parámetros para el aire:
dónde:
- q c es la presión dinámica medida detrás de un amortiguador normal.
Como se puede ver, M aparece en ambos lados de la ecuación, y para fines prácticos se debe utilizar un algoritmo de búsqueda de raíces para una solución numérica (la ecuación es una ecuación séptica en M 2 y, aunque algunas de estas pueden resolverse explícitamente, el teorema de Abel-Ruffini garantiza que no existe una forma general para las raíces de estos polinomios). Primero se determina si M es de hecho mayor que 1.0 calculando M a partir de la ecuación subsónica. Si M es mayor que 1.0 en ese punto, entonces el valor de M de la ecuación subsónica se utiliza como condición inicial para la iteración de punto fijo de la ecuación supersónica, que generalmente converge muy rápidamente. [9] Alternativamente, también se puede utilizar el método de Newton .
Véase también
- Número crítico de Mach : concepto en aerodinámica
- Machmeter – Instrumento de vuelo
- Ramjet – Motor a reacción atmosférico supersónico
- Scramjet – Motor a reacción en el que la combustión se produce en un flujo de aire supersónico
- Velocidad del sonido – Velocidad de la onda sonora a través de un medio elástico
- Velocidad aerodinámica real : velocidad de una aeronave en relación con la masa de aire a través de la cual está volando.
- Órdenes de magnitud (velocidad) : comparación de una amplia gama de velocidades
Notas
- ^ ab Young, Donald F.; Munson, Bruce R.; Okiishi, Theodore H .; Huebsch, Wade W. (21 de diciembre de 2010). Una breve introducción a la mecánica de fluidos (5.ª ed.). John Wiley & Sons. pág. 95. ISBN 978-0-470-59679-1. LCCN 2010038482. OCLC 667210577. OL 24479108M.
- ^ ab Graebel, William P. (19 de enero de 2001). Ingeniería mecánica de fluidos (1.ª ed.). CRC Press . p. 16. ISBN 978-1-56032-733-2. OCLC 1034989004. OL 9794889M.
- ^ "Ernst Mach". Encyclopædia Britannica . 2016 . Consultado el 6 de enero de 2016 .
- ^ Jakob Ackeret: Der Luftwiderstand bei sehr großen Geschwindigkeiten. Schweizerische Bauzeitung 94 (octubre de 1929), págs. 179-183. Véase también: N. Rott: Jakob Ackert y la historia del número de Mach. Revisión anual de mecánica de fluidos 17 (1985), págs.
- ^ Bodie, Warren M., El Lockheed P-38 Lightning , Widewing Publications ISBN 0-9629359-0-5 .
- ^ Nancy Hall (ed.). "Número de Mach". NASA .
- ^ Clancy, LJ (1975), Aerodinámica, Tabla 1, Pitman Publishing London, ISBN 0-273-01120-0
- ^ Kundu, PJ; Cohen, IM; Dowling, DR (2012). Mecánica de fluidos (5.ª ed.). Academic Press. págs. 148-149. ISBN 978-0-12-382100-3.
- ^ abc Olson, Wayne M. (2002). "AFFTC-TIH-99-02, Pruebas de vuelo de rendimiento de aeronaves ". (PDF). Centro de pruebas de vuelo de la Fuerza Aérea, Edwards AFB, CA, Fuerza Aérea de los Estados Unidos. Archivado el 4 de septiembre de 2011 en Wayback Machine .
Enlaces externos
- Caja de herramientas de dinámica de gases Calcule el número de Mach y los parámetros de onda de choque normales para mezclas de gases perfectos e imperfectos.
- Página de la NASA sobre el número de Mach Calculadora interactiva para el número de Mach.
- Calculadora de atmósfera estándar y convertidor de velocidad NewByte






















![{\displaystyle \mathrm {M} ={\sqrt {{\frac {2}{\gamma -1}}[\left({\frac {q_{c}}{p}}+1\right)^{\frac {\gamma -1}{\gamma }}-1\right]}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6cfb0b14f5726032a386928f8312725a3325c4c)
![{\displaystyle {\frac {p_{t}}{p}}=\left[{\frac {\gamma +1}{2}}\mathrm {M} ^{2}\right]^{\frac {\gamma }{\gamma -1}}\cdot \left[{\frac {\gamma +1}{1-\gamma +2\gamma \,\mathrm {M} ^{2}}}\right]^{\frac {1}{\gamma -1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e40925c7d73812aaeb7be0541fb045abfe268c54)
![{\displaystyle \mathrm {M} ={\sqrt {5\left[\left({\frac {q_{c}}{p}}+1\right)^{\frac {2}{7}}-1\right]}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbbe331c3f8c63b187b0a3a3fc23580e4cb2ac55)
