Problema de celosía
Problema de optimización en informática

En informática , los problemas de celosía son una clase de problemas de optimización relacionados con objetos matemáticos llamados retículos . La supuesta intratabilidad de tales problemas es fundamental para la construcción de criptosistemas seguros basados ​​en retículos : los problemas de celosía son un ejemplo de problemas NP-difíciles que han demostrado ser difíciles en el caso promedio , lo que proporciona un caso de prueba para la seguridad de los algoritmos criptográficos. Además, algunos problemas de celosía que son difíciles en el peor de los casos se pueden utilizar como base para esquemas criptográficos extremadamente seguros. El uso de la dureza del peor de los casos en tales esquemas los convierte en uno de los pocos esquemas que es muy probable que sean seguros incluso contra las computadoras cuánticas . Para aplicaciones en tales criptosistemas , generalmente se consideran retículos sobre espacios vectoriales (a menudo ) o módulos libres (a menudo ). Q norte {\displaystyle \mathbb {Q} ^{n}} O norte {\displaystyle \mathbb {Z} ^{n}}

Para todos los problemas que se presentan a continuación, supongamos que se nos proporciona (además de otras entradas más específicas) una base para el espacio vectorial V y una norma N. La norma que se considera habitualmente es la norma euclidiana L 2 . Sin embargo, también se consideran otras normas (como L p ) que aparecen en una variedad de resultados. [1]

A lo largo de este artículo, denotemos la longitud del vector distinto de cero más corto en la red L : es decir, la ( yo ) {\displaystyle \lambda (L)}

la ( yo ) = mín. en ∈ yo ∖ { 0 } " en " norte . {\displaystyle \lambda (L)=\min _{v\in L\smallsetminus \{\mathbf {0} \}}\|v\|_{N}.}

Problema del vector más corto (SVP)

Esta es una ilustración del problema del vector más corto (vectores base en azul, vector más corto en rojo).

En el SVP, se dan una base de un espacio vectorial V y una norma N (a menudo L 2 ) para una red L y se debe encontrar el vector distinto de cero más corto en V , medido por N , en L . En otras palabras, el algoritmo debe generar un vector distinto de cero v tal que ⁠ ⁠ " en " norte = la ( yo ) {\displaystyle \|v\|_{N}=\lambda (L)} .

En la versión de aproximación γ SVP γ , se debe encontrar un vector reticular distinto de cero de longitud como máximo para ⁠ ⁠ dado . gamma ⋅ la ( yo ) {\displaystyle \gamma \cdot \lambda (L)} gamma ≥ 1 {\displaystyle \gamma \geq 1}

Resultados de dureza

Sólo se sabe que la versión exacta del problema es NP-difícil para reducciones aleatorias. [2] [3] Por el contrario, se sabe que el problema correspondiente con respecto a la norma uniforme es NP-difícil . [4]

Algoritmos para la norma euclidiana

Para resolver la versión exacta del SVP bajo la norma euclidiana, se conocen varios enfoques diferentes, que se pueden dividir en dos clases: algoritmos que requieren tiempo superexponencial ( ) y memoria, y algoritmos que requieren tiempo y espacio exponenciales ( ) en la dimensión reticular. La primera clase de algoritmos incluye principalmente la enumeración reticular [5] [6] [7] y la reducción de muestreo aleatorio, [8] [9] mientras que la última incluye el tamizado reticular, [10] [11] [12] calculando la celda de Voronoi de la red, [13] [14] y el muestreo gaussiano discreto. [15] Un problema abierto es si existen algoritmos para resolver el SVP exacto que se ejecuten en tiempo exponencial simple ( ) y requieran escalamiento de memoria polinomialmente en la dimensión reticular. [16] 2 ω ( norte ) {\displaystyle 2^{\omega (n)}} escuela politécnica ⁡ ( norte ) {\displaystyle \operatorname {poli} (n)} 2 O ( norte ) {\displaystyle 2^{\Theta (n)}} 2 Oh ( norte ) {\displaystyle 2^{O(n)}}

Para resolver la versión de aproximación γ SVP γ para la norma euclidiana, los enfoques más conocidos se basan en el uso de la reducción de base reticular . Para valores grandes de ⁠ ⁠ , el algoritmo Lenstra–Lenstra–Lovász (LLL) puede encontrar una solución en un polinomio temporal en la dimensión reticular. Para valores más pequeños de , se utiliza comúnmente el algoritmo Block Korkine-Zolotarev (BKZ) [17] [18] [19] , donde la entrada al algoritmo (el tamaño del bloque ) determina la complejidad temporal y la calidad de la salida: para factores de aproximación grandes , basta con un tamaño de bloque pequeño y el algoritmo termina rápidamente. Para valores pequeños , se necesitan tamaños de bloque más grandes para encontrar vectores reticulares suficientemente cortos, y el algoritmo tarda más en encontrar una solución. El algoritmo BKZ utiliza internamente un algoritmo SVP exacto como subrutina (que se ejecuta en redes de dimensión como máximo ), y su complejidad general está estrechamente relacionada con los costos de estas llamadas SVP en dimensión ⁠ ⁠ . gamma > 1 {\displaystyle \gamma >1} gamma = 2 Ohmio ( norte ) {\displaystyle \gamma =2^{\Omega (n)}} gamma {\estilo de visualización \gamma} β {\estilo de visualización \beta} gamma {\estilo de visualización \gamma} β {\estilo de visualización \beta} gamma {\estilo de visualización \gamma} β {\estilo de visualización \beta} β {\estilo de visualización \beta} β {\estilo de visualización \beta}

GapSVP

El problema GapSVP β consiste en distinguir entre las instancias de SVP en las que la longitud del vector más corto es como máximo o mayor que ⁠ ⁠ , donde puede ser una función fija de la dimensión de la red ⁠ ⁠ . Dada una base para la red, el algoritmo debe decidir si ⁠ ⁠ . Al igual que otros problemas de promesa , el algoritmo puede equivocarse en todos los demás casos. 1 {\estilo de visualización 1} β {\estilo de visualización \beta} β {\estilo de visualización \beta} norte {\estilo de visualización n} la ( yo ) ≤ 1 {\displaystyle \lambda (L)\leq 1} la ( yo ) > β {\displaystyle \lambda (L)>\beta }

Otra versión del problema es GapSVP ζ,γ para algunas funciones ζ y γ. La entrada al algoritmo es una base y un número . Se asegura que todos los vectores en la ortogonalización de Gram-Schmidt tienen una longitud de al menos 1, y que y que ⁠ ⁠ , donde es la dimensión. El algoritmo debe aceptar si ⁠ ⁠ , y rechazar si ⁠ ⁠ . Para valores grandes (es decir, ⁠ ⁠ ), el problema es equivalente a GapSVP γ porque [20] un preprocesamiento realizado utilizando el algoritmo LLL hace que la segunda condición (y, por lo tanto, ⁠ ⁠ ) sea redundante. B {\estilo de visualización B} d {\estilo de visualización d} la ( yo ( B ) ) ≤ o ( norte ) {\displaystyle \lambda (L(B))\leq \zeta (n)} 1 ≤ d ≤ o ( norte ) / gamma ( norte ) {\displaystyle 1\leq d\leq \zeta (n)/\gamma (n)} norte {\estilo de visualización n} la ( yo ( B ) ) ≤ d {\displaystyle \lambda(L(B))\leq d} la ( yo ( B ) ) ≥ gamma ( norte ) ⋅ d {\displaystyle \lambda (L(B))\geq \gamma (n)\cdot d} o {\estilo de visualización \zeta} o ( norte ) > 2 norte / 2 {\displaystyle \zeta (n)>2^{n/2}} o {\estilo de visualización \zeta}

Problema del vector más cercano (CVP)

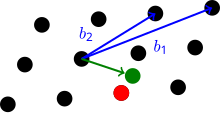
Esta es una ilustración del problema del vector más cercano (vectores base en azul, vector externo en verde, vector más cercano en rojo).

En CVP, se dan una base de un espacio vectorial V y una métrica M (a menudo L 2 ) para una red L , así como un vector v en V pero no necesariamente en L . Se desea encontrar el vector en L más cercano a v (medido por M ). En la versión de aproximación CVP γ , se debe encontrar un vector de red a una distancia como máximo . gamma {\estilo de visualización \gamma} gamma {\estilo de visualización \gamma}

Relación con SVP

El problema del vector más cercano es una generalización del problema del vector más corto. Es fácil demostrar que, dado un oráculo para CVP γ (definido a continuación), se puede resolver SVP γ haciendo algunas consultas al oráculo. [21] El método ingenuo para encontrar el vector más corto llamando al oráculo CVP γ para encontrar el vector más cercano a 0 no funciona porque 0 es en sí mismo un vector reticular y el algoritmo podría potencialmente dar como resultado 0.

La reducción de SVP γ a CVP γ es la siguiente: supongamos que la entrada a SVP γ es la base de la red . Consideremos la base y sea el vector devuelto por CVP γ ( B i , b i ) . La afirmación es que el vector más corto del conjunto es el vector más corto de la red dada. B = [ b 1 , b 2 , … , b norte ] {\displaystyle B=[b_{1},b_{2},\ldots ,b_{n}]} B i = [ b 1 , … , 2 b i , … , b norte ] {\displaystyle B^{i}=[b_{1},\ldots ,2b_{i},\ldots ,b_{n}]} incógnita i Estilo de visualización x_{i}} { incógnita i − b i } Estilo de visualización: x-b

Resultados de dureza

Goldreich et al. demostraron que cualquier dureza de SVP implica la misma dureza para CVP. [22] Utilizando herramientas PCP , Arora et al. demostraron que CVP es difícil de aproximar dentro del factor a menos que . [23] Dinur et al. reforzaron esto al dar un resultado de dureza NP con para . [24] 2 registro 1 − o ⁡ ( norte ) {\displaystyle 2^{\log ^{1-\epsilon }(n)}} notario público ⊆ TIEMPO DT ⁡ ( 2 escuela politécnica ⁡ ( registro ⁡ norte ) ) {\displaystyle \operatorname {NP} \subseteq \operatorname {DTIME} (2^{\operatorname {poly} (\log n)})} o = ( registro ⁡ registro ⁡ norte ) do {\displaystyle \epsilon = (\log \log n)^{c}} do < 1 / 2 {\estilo de visualización c<1/2}

Descodificación de esferas

Los algoritmos para CVP, especialmente la variante de Fincke y Pohst, [6] se han utilizado para la detección de datos en sistemas de comunicación inalámbrica de múltiples entradas y múltiples salidas ( MIMO ) (para señales codificadas y no codificadas). [25] [13] En este contexto, se denomina decodificación de esfera debido al radio utilizado internamente en muchas soluciones CVP. [26]

Se ha aplicado en el campo de la resolución de ambigüedad de números enteros en GNSS (GPS) de fase portadora. [27] En ese campo se denomina método LAMBDA . En el mismo campo, el problema CVP general se conoce como Mínimos cuadrados enteros .

Brecha CVP

Este problema es similar al problema GapSVP. Para GapSVP β , la entrada consiste en una base reticular y un vector , y el algoritmo debe responder si se cumple una de las siguientes condiciones: en {\estilo de visualización v}

  • existe un vector reticular tal que la distancia entre él y es como máximo 1, y en {\estilo de visualización v}
  • Cada vector reticular está a una distancia mayor que de . β {\estilo de visualización \beta} en {\estilo de visualización v}

La condición opuesta es que el vector reticular más cercano esté a una distancia , de ahí el nombre CVP de Gap . 1 < la ( yo ) ≤ β {\displaystyle 1<\lambda (L)\leq \beta }

Resultados conocidos

El problema está trivialmente contenido en NP para cualquier factor de aproximación.

Schnorr , en 1987, demostró que los algoritmos de tiempo polinomial deterministas pueden resolver el problema para . [28] Ajtai et al. demostraron que los algoritmos probabilísticos pueden lograr un factor de aproximación ligeramente mejor de . [10] β = 2 Oh ( norte ( registro ⁡ registro ⁡ norte ) 2 / registro ⁡ norte ) {\displaystyle \beta = 2^{O(n(\log \log n)^{2}/\log n)}} β = 2 Oh ( norte registro ⁡ registro ⁡ norte / registro ⁡ norte ) {\displaystyle \beta = 2^{O(n\log \log n/\log n)}}

En 1993, Banaszczyk demostró que GapCVP n está en . [29] En 2000, Goldreich y Goldwasser demostraron que pone el problema tanto en NP como en coAM . [30] En 2005, Aharonov y Regev demostraron que para alguna constante , el problema con está en . [31] norte PAG ∩ do o norte PAG {\displaystyle {\mathsf {NP\cap coNP}}} β = norte / registro ⁡ norte {\displaystyle \beta ={\sqrt {n/\log n}}} do {\estilo de visualización c} β = do norte {\displaystyle \beta = c{\sqrt {n}}} norte PAG ∩ do o norte PAG {\displaystyle {\mathsf {NP\cap coNP}}}

Para los límites inferiores, Dinur et al. demostraron en 1998 que el problema es NP-difícil para . [32] β = norte o ( 1 / registro ⁡ registro ⁡ norte ) {\displaystyle \beta =n^{o(1/\log {\log {n}})}}

Problema de los vectores independientes más cortos (SIVP)

Dada una red L de dimensión n , el algoritmo debe generar n linealmente independiente de modo que , donde el lado derecho considera todas las bases de la red. en 1 , en 2 , … , en norte {\displaystyle v_{1},v_{2},\ldots,v_{n}} máximo " en i " ≤ máximo B " b i " {\displaystyle \max \|v_{i}\|\leq \max _{B}\|b_{i}\|} B = { b 1 , … , b norte } {\displaystyle B=\{b_{1},\ldots ,b_{n}\}}

En la versión aproximada, dada una red L con dimensión n , se deben encontrar n vectores linealmente independientes de longitud ⁠ ⁠ , donde es el ⁠ ⁠ ésimo mínimo sucesivo de ⁠ ⁠ . gamma {\estilo de visualización \gamma} en 1 , en 2 , … , en norte {\displaystyle v_{1},v_{2},\ldots,v_{n}} máximo " en i " ≤ gamma la norte ( yo ) {\displaystyle \max \|v_{i}\|\leq \gamma \lambda _{n}(L)} la norte ( yo ) {\displaystyle \lambda _ {n}(L)} norte {\estilo de visualización n} yo {\estilo de visualización L}

Descodificación de distancias limitadas

Este problema es similar al CVP. Dado un vector cuya distancia a la red es como máximo , el algoritmo debe generar el vector de red más cercano a él. la ( yo ) / 2 {\displaystyle \lambda (L)/2}

Problema del radio de cobertura

Dada una base para la red, el algoritmo debe encontrar la distancia más grande (o en algunas versiones, su aproximación) desde cualquier vector a la red.

Problema de la base más corta

Muchos problemas se vuelven más fáciles si la base de entrada consiste en vectores cortos. Un algoritmo que resuelve el problema de la base más corta (SBP) debe, dada una base reticular , generar B {\estilo de visualización B} una base equivalente tal que la longitud del vector más largo sea lo más corta posible. B " {\estilo de visualización B'} B " {\estilo de visualización B'}

La versión de aproximación del problema SBP γ consiste en encontrar una base cuyo vector más largo sea, como máximo, más largo que el vector más largo en la base más corta. gamma {\estilo de visualización \gamma}

Uso en criptografía

La dureza promedio de los problemas constituye una base para las pruebas de seguridad de la mayoría de los esquemas criptográficos. Sin embargo, la evidencia experimental sugiere que la mayoría de los problemas NP-hard carecen de esta propiedad: probablemente solo sean difíciles en el peor de los casos. Se ha conjeturado o demostrado que muchos problemas de red son difíciles en el peor de los casos, lo que los convierte en una clase atractiva de problemas en los que basar esquemas criptográficos. Además, la dureza del peor de los casos de algunos problemas de red se ha utilizado para crear esquemas criptográficos seguros. El uso de la dureza del peor de los casos en tales esquemas los convierte en uno de los pocos esquemas que es muy probable que sean seguros incluso contra las computadoras cuánticas .

Los problemas de red anteriores son fáciles de resolver si se proporciona al algoritmo una base "buena". Los algoritmos de reducción de red apuntan, dada una base para una red, a generar una nueva base que consista en vectores relativamente cortos y casi ortogonales . El algoritmo de reducción de base de red de Lenstra–Lenstra–Lovász (LLL) fue uno de los primeros algoritmos eficientes para este problema que podía generar una base de red casi reducida en tiempo polinomial. [33] Este algoritmo y sus posteriores refinamientos se utilizaron para romper varios esquemas criptográficos, estableciendo su estatus como una herramienta muy importante en el criptoanálisis. El éxito de LLL en datos experimentales llevó a creer que la reducción de red podría ser un problema fácil en la práctica; sin embargo, esta creencia fue cuestionada a fines de la década de 1990, cuando se obtuvieron varios resultados nuevos sobre la dificultad de los problemas de red, comenzando con el resultado de Ajtai . [2]

En sus artículos seminales, Ajtai demostró que el problema SVP era NP-hard y descubrió algunas conexiones entre la complejidad del peor caso y la complejidad del caso promedio de algunos problemas de red. [2] [3] Basándose en estos resultados, Ajtai y Dwork crearon un criptosistema de clave pública cuya seguridad podría probarse utilizando solo la dureza del peor caso de una cierta versión de SVP, [34] convirtiéndolo así en el primer resultado en haber utilizado la dureza del peor caso para crear sistemas seguros. [35]

Véase también

Referencias

  1. ^ Khot, Subhash (2005). "Dificultad de aproximación del problema del vector más corto en redes". J. ACM . 52 (5): 789–808. doi :10.1145/1089023.1089027. S2CID  13438130.
  2. ^ abc Ajtai, M. (1996). "Generación de instancias difíciles de problemas de red". Actas del vigésimo octavo simposio anual de la ACM sobre teoría de la computación . Filadelfia, Pensilvania, Estados Unidos: ACM. págs. 99–108. doi :10.1145/237814.237838. ISBN 978-0-89791-785-8.S2CID6864824  .​
  3. ^ ab Ajtai, Miklós (1998). "El problema del vector más corto en L2 es NP-duro para reducciones aleatorias". Actas del trigésimo simposio anual de la ACM sobre teoría de la computación . Dallas, Texas, Estados Unidos: ACM. pp. 10–19. doi :10.1145/276698.276705. ISBN 978-0-89791-962-3. Número de identificación del sujeto  4503998.
  4. ^ van Emde Boas, Peter (1981). "Otro problema NP-completo y la complejidad de calcular vectores cortos en una red". Informe técnico 8104. Universidad de Ámsterdam, Departamento de Matemáticas, Países Bajos.
  5. ^ Kannan, Ravi (1983). "Algoritmos mejorados para programación entera y problemas de red relacionados". Actas del decimoquinto simposio anual de la ACM sobre teoría de la computación - STOC '83 . Nueva York, NY, EE. UU.: ACM. págs. 193–206. doi :10.1145/800061.808749. ISBN 978-0-89791-099-6.ID S2C  18181112.
  6. ^ ab Fincke, U.; Pohst, M. (1985). "Métodos mejorados para calcular vectores de longitud corta en una red, incluido un análisis de complejidad". Math. Comp . 44 (170): 463–471. doi : 10.1090/S0025-5718-1985-0777278-8 .
  7. ^ Gama, Nicolas; Nguyen, Phong Q.; Regev, Oded (30 de mayo de 2010). "Enumeración de retículas mediante poda extrema". Avances en criptología – EUROCRYPT 2010. Apuntes de clase en informática. Vol. 6110. Springer, Berlín, Heidelberg. págs. 257–278. doi :10.1007/978-3-642-13190-5_13. ISBN 978-3-642-13189-9. Número de identificación del sujeto  1938519.
  8. ^ Schnorr, Claus Peter (27 de febrero de 2003). "Reducción de red mediante muestreo aleatorio y métodos de cumpleaños". Stacs 2003. Lecture Notes in Computer Science. Vol. 2607. Springer, Berlín, Heidelberg. págs. 145–156. CiteSeerX 10.1.1.137.4293 . doi :10.1007/3-540-36494-3_14. ISBN .  978-3-540-36494-8.
  9. ^ Aono, Yoshinori; Nguyen, Phong Q. (30 de abril de 2017). "Revisión del muestreo aleatorio: enumeración en red con poda discreta". Avances en criptología – EUROCRYPT 2017 (PDF) . Apuntes de clase en informática. Vol. 10211. Springer, Cham. págs. 65–102. doi :10.1007/978-3-319-56614-6_3. ISBN 978-3-319-56613-9. Número de identificación del sujeto  39082279.
  10. ^ ab Ajtai, Miklós; Kumar, Ravi; Sivakumar, D. (2001). "Un algoritmo de tamiz para el problema del vector reticular más corto". Actas del trigésimo tercer simposio anual de la ACM sobre teoría de la computación . Hersonissos, Grecia: ACM. págs. 601–610. doi :10.1145/380752.380857. ISBN 1-58113-349-9.S2CID 14982298  .
  11. ^ Micciancio, Daniele; Voulgaris, Panagiotis (2010). "Algoritmos de tiempo exponencial más rápidos para el problema del vector más corto". Actas del vigésimo primer simposio anual ACM-SIAM sobre algoritmos discretos . SODA '10. Filadelfia, PA, EE. UU.: Society for Industrial and Applied Mathematics. págs. 1468–1480. doi : 10.1137/1.9781611973075.119 . ISBN . 978-0-89871-698-6.S2CID 90084  .
  12. ^ Becker, A.; Ducas, L.; Gama, N.; Laarhoven, T. (21 de diciembre de 2015). "Nuevas direcciones en la búsqueda del vecino más cercano con aplicaciones al tamizado en red". Actas del vigésimo séptimo simposio anual ACM-SIAM sobre algoritmos discretos. Sociedad de Matemáticas Industriales y Aplicadas. págs. 10–24. doi :10.1137/1.9781611974331.ch2. ISBN 978-1-61197-433-1.
  13. ^ ab Agrell, E.; Eriksson, T.; Vardy, A.; Zeger, K. (2002). "Búsqueda del punto más cercano en redes" (PDF) . IEEE Trans. Inf. Theory . 48 (8): 2201–2214. doi :10.1109/TIT.2002.800499.
  14. ^ Micciancio, Daniele; Voulgaris, Panagiotis (2010). "Un algoritmo determinista de tiempo exponencial simple para la mayoría de los problemas de red basados ​​en cálculos de celdas de Voronoi". Actas del cuadragésimo segundo simposio de la ACM sobre teoría de la computación . STOC '10. Nueva York, NY, EE. UU.: ACM. pp. 351–358. CiteSeerX 10.1.1.705.3304 . doi :10.1145/1806689.1806739. ISBN .  978-1-4503-0050-6.S2CID2449948  .​
  15. ^ Aggarwal, Divesh; Dadush, Daniel; Regev, Oded; Stephens-Davidowitz, Noah (2015). "Resolución del problema del vector más corto en 2 n de tiempo mediante muestreo gaussiano discreto". Actas del cuadragésimo séptimo simposio anual de la ACM sobre teoría de la computación. STOC '15. Nueva York, NY, EE. UU.: ACM. págs. 733–742. doi :10.1145/2746539.2746606. ISBN 978-1-4503-3536-2.S2CID10214330  .​
  16. ^ Micciancio, Daniele (1 de julio de 2017). "Criptografía en red: problema del vector más corto".
  17. ^ Schnorr, CP (1987-01-01). "Una jerarquía de algoritmos de reducción de base de red temporal polinómica". Ciencias Informáticas Teóricas . 53 (2): 201–224. doi : 10.1016/0304-3975(87)90064-8 .
  18. ^ Schnorr, CP; Euchner, M. (1994-08-01). "Reducción de la base reticular: algoritmos prácticos mejorados y resolución de problemas de suma de subconjuntos" (PDF) . Programación matemática . 66 (1–3): 181–199. doi :10.1007/bf01581144. ISSN  0025-5610. S2CID  15386054.
  19. ^ Chen, Yuanmi; Nguyen, Phong Q. (4 de diciembre de 2011). "BKZ 2.0: mejores estimaciones de seguridad de la red". Avances en criptología – ASIACRYPT 2011. Apuntes de clase en informática. Vol. 7073. Springer, Berlín, Heidelberg. págs. 1–20. doi :10.1007/978-3-642-25385-0_1. ISBN 978-3-642-25384-3.
  20. ^ Peikert, Chris (2009). "Sistemas de criptografía de clave pública a partir del problema del vector más corto en el peor de los casos: resumen ampliado". Actas del 41.º simposio anual de la ACM sobre teoría de la computación. Bethesda, MD, EE. UU.: ACM. pp. 333–342. doi :10.1145/1536414.1536461. ISBN 978-1-60558-506-2.S2CID 1864880  .
  21. ^ Micciancio, Daniele; Goldwasser, Shafi (2002). Complejidad de los problemas de celosía . Saltador.
  22. ^ Goldreich, O.; et al. (1999). "Aproximar los vectores reticulares más cortos no es más difícil que aproximar los vectores reticulares más cercanos". Inf. Process. Lett . 71 (2): 55–61. doi :10.1016/S0020-0190(99)00083-6.
  23. ^ Arora, Sanjeev; et al. (1993). "Actas de la 34.ª edición anual de 1993 de la IEEE sobre fundamentos de la informática". J. Comput. Syst. Sci . Vol. 54. págs. 317–331. doi :10.1109/SFCS.1993.366815. ISBN . 978-0-8186-4370-5.S2CID44988406  .​
  24. ^ Dinur, I.; et al. (2003). "Aproximar el CVP a factores casi polinomiales es NP-difícil". Combinatorica . 23 (2): 205–243. doi :10.1007/s00493-003-0019-y. S2CID  45754954.
  25. ^ Biglieri, E.; Calderbank, R.; Constantinides, Anthony G .; Goldsmith, A.; Paulraj, A.; Poor, H. V. (2007). Comunicaciones inalámbricas MIMO . Cambridge: Cambridge UP.
  26. ^ Wang, Ping; Le-Ngoc, Tho (2011). "Un algoritmo de decodificación de esferas de lista con estrategias de configuración de radio mejoradas". Comunicaciones personales inalámbricas . 61 (1): 189–200. doi :10.1007/s11277-010-0018-4. S2CID  30919872.
  27. ^ Hassibi, A.; Boyd, S. (1998). "Estimación de parámetros enteros en modelos lineales con aplicaciones al GPS". IEEE Trans. Sig. Proc . 46 (11): 2938–2952. Bibcode :1998ITSP...46.2938H. CiteSeerX 10.1.1.114.7246 . doi :10.1109/78.726808. 
  28. ^ Schnorr, CP "Factorización de números enteros y cálculo de logaritmos discretos mediante aproximación diofántica". Avances en criptología – Actas de Eurocrypt '91 .
  29. ^ Banaszczyk, W. (1993). "Nuevos límites en algunos teoremas de transferencia en la geometría de números". Math. Ann. 296 (1): 625–635. doi :10.1007/BF01445125. S2CID  13921988.
  30. ^ Goldreich, Oded; Goldwasser, Shafi (1998). "Sobre los límites de la no aproximabilidad de los problemas de red". Actas del trigésimo simposio anual de la ACM sobre teoría de la computación . Dallas, Texas, Estados Unidos: ACM. pp. 1–9. doi :10.1145/276698.276704. ISBN 0-89791-962-9.S2CID3051993  .​
  31. ^ Aharonov, Dorit; Oded Regev (2005). "Problemas de celosía en NP coNP". J. ACM . 52 (5): 749–765. CiteSeerX 10.1.1.205.3730 . doi :10.1145/1089023.1089025. S2CID  1669286. ∩ {\displaystyle \cap}  
  32. ^ Dinur, I.; Kindler, G.; Safra, S. (1998). "Aproximar el CVP a factores casi polinomiales es NP-difícil". Actas del 39.° Simposio anual sobre fundamentos de la informática . IEEE Computer Society. pág. 99. ISBN 978-0-8186-9172-0.
  33. ^ Lenstra, AK; Lenstra, HW Jr.; Lovász, L. (1982). "Factorización de polinomios con coeficientes racionales" (PDF) . Math. Ann. 261 (4): 515–534. doi :10.1007/BF01457454. S2CID  5701340. Archivado desde el original (PDF) el 17 de julio de 2011.
  34. ^ Ajtai, Miklós; Dwork, Cynthia (1997). "Un criptosistema de clave pública con equivalencia entre el peor de los casos y el caso promedio". Actas del vigésimo noveno simposio anual de la ACM sobre teoría de la computación . El Paso, Texas, Estados Unidos: ACM. pp. 284–293. doi :10.1145/258533.258604. ISBN . 0-89791-888-6.S2CID 9918417  .
  35. ^ Cai, Jin-Yi (2000). "La complejidad de algunos problemas de retícula". Teoría de números algorítmica . Apuntes de clase en informática. Vol. 1838. págs. 1–32. doi :10.1007/10722028_1. ISBN 978-3-540-67695-9.

Lectura adicional

  • Agrell, E.; Eriksson, T.; Vardy, A.; Zeger, K. (2002). "Búsqueda del punto más cercano en redes" (PDF) . IEEE Trans. Inf. Theory . 48 (8): 2201–2214. doi :10.1109/TIT.2002.800499.
  • Micciancio, Daniele (2001). "El problema del vector más corto es {NP}-difícil de aproximar dentro de alguna constante". Revista SIAM de Computación . 30 (6): 2008–2035. CiteSeerX  10.1.1.93.6646 . doi :10.1137/S0097539700373039. S2CID  42794945.
  • Nguyen, Phong Q.; Stern, Jacques (2000). "Reducción de retículos en criptología: una actualización". Actas del 4º Simposio internacional sobre teoría algorítmica de números . Springer-Verlag. págs. 85–112. ISBN 978-3-540-67695-9.
Obtenido de "https://es.wikipedia.org/w/index.php?title=Problema_de_la_red&oldid=1220103473"