Modelo de neurona biológica
Este artículo tiene varios problemas. Ayúdenos a mejorarlo o a discutir estos problemas en la página de discusión . ( Aprenda cómo y cuándo eliminar estos mensajes )
|

Los modelos neuronales biológicos , también conocidos como modelos de neuronas en pico , [1] son descripciones matemáticas de la conducción de señales eléctricas en las neuronas . Las neuronas (o células nerviosas) son células eléctricamente excitables dentro del sistema nervioso , capaces de disparar señales eléctricas, llamadas potenciales de acción , a través de una red neuronal. Estos modelos matemáticos describen el papel de las características biofísicas y geométricas de las neuronas en la conducción de la actividad eléctrica.
Central para estos modelos es la descripción de cómo el potencial de membrana (es decir, la diferencia en el potencial eléctrico entre el interior y el exterior de una célula biológica ) a través de la membrana celular cambia con el tiempo. En un entorno experimental, estimular las neuronas con una corriente eléctrica genera un potencial de acción (o pico), que se propaga por el axón de la neurona . Este axón puede ramificarse y conectarse a una gran cantidad de neuronas aguas abajo en sitios llamados sinapsis . En estas sinapsis, el pico puede causar la liberación de neurotransmisores , que a su vez pueden cambiar el potencial de voltaje de las neuronas aguas abajo. Este cambio puede conducir potencialmente a incluso más picos en esas neuronas aguas abajo, transmitiendo así la señal. Hasta el 85% de las neuronas en el neocórtex , la capa más externa del cerebro de los mamíferos , consisten en neuronas piramidales excitatorias , [2] [3] y cada neurona piramidal recibe decenas de miles de entradas de otras neuronas. [4] Por lo tanto, las neuronas activas son una unidad importante de procesamiento de información del sistema nervioso .
Un ejemplo de un modelo de neurona en pico puede ser un modelo matemático muy detallado que incluya morfología espacial . Otro puede ser un modelo de neurona basado en la conductancia que considere a las neuronas como puntos y describa la dinámica del voltaje de la membrana como una función de las corrientes transmembrana. Un modelo matemáticamente más simple de "integración y disparo" simplifica significativamente la descripción de la dinámica del canal iónico y del potencial de membrana (inicialmente estudiado por Lapique en 1907). [5] [6]
Antecedentes biológicos, clasificación y objetivos de los modelos neuronales
Células no espiculares, células espiculares y su medición
No todas las células del sistema nervioso producen el tipo de pico que define el alcance de los modelos de neuronas con picos. Por ejemplo, las células ciliadas cocleares , las células receptoras de la retina y las células bipolares de la retina no producen picos. Además, muchas células del sistema nervioso no se clasifican como neuronas, sino como glía .
La actividad neuronal se puede medir con diferentes técnicas experimentales, como la técnica de medición de "célula completa", que captura la actividad de disparo de una sola neurona y produce potenciales de acción de amplitud completa.
Con las técnicas de medición extracelular, se colocan uno o más electrodos en el espacio extracelular . Los picos, a menudo de varias fuentes de picos, según el tamaño del electrodo y su proximidad a las fuentes, se pueden identificar con técnicas de procesamiento de señales. La medición extracelular tiene varias ventajas:
- Es más fácil de obtener experimentalmente;
- Es robusto y dura más tiempo;
- Puede reflejar el efecto dominante, especialmente cuando se realiza en una región anatómica con muchas células similares.
Descripción general de los modelos neuronales
Los modelos neuronales se pueden dividir en dos categorías según las unidades físicas de la interfaz del modelo. Cada categoría se puede dividir a su vez según el nivel de abstracción/detalle:
- Modelos de voltaje de entrada-salida de membrana eléctrica: estos modelos producen una predicción del voltaje de salida de membrana como una función de la estimulación eléctrica dada como entrada de corriente o voltaje. Los diversos modelos de esta categoría difieren en la relación funcional exacta entre la corriente de entrada y el voltaje de salida y en el nivel de detalle. Algunos modelos de esta categoría predicen solo el momento de ocurrencia del pico de salida (también conocido como "potencial de acción"); otros modelos son más detallados y dan cuenta de los procesos subcelulares. Los modelos de esta categoría pueden ser deterministas o probabilísticos.
- Modelos de neuronas de entrada con estímulos naturales o farmacológicos: los modelos de esta categoría relacionan el estímulo de entrada, que puede ser farmacológico o natural, con la probabilidad de un evento de pico. La etapa de entrada de estos modelos no es eléctrica, sino que tiene unidades de concentración farmacológicas (químicas) o unidades físicas que caracterizan un estímulo externo, como la luz, el sonido u otras formas de presión física. Además, la etapa de salida representa la probabilidad de un evento de pico y no un voltaje eléctrico.
Aunque no es inusual en ciencia e ingeniería tener varios modelos descriptivos para diferentes niveles de abstracción/detalle, la cantidad de modelos neuronales biológicos diferentes, a veces contradictorios, es excepcionalmente alta. Esta situación es en parte resultado de los muchos entornos experimentales diferentes y de la dificultad de separar las propiedades intrínsecas de una sola neurona de los efectos de medición e interacciones de muchas células ( efectos de red ).
Objetivos de los modelos neuronales
En última instancia, los modelos neuronales biológicos tienen como objetivo explicar los mecanismos que subyacen al funcionamiento del sistema nervioso. Sin embargo, se pueden distinguir varios enfoques, desde modelos más realistas (por ejemplo, modelos mecanicistas) hasta modelos más pragmáticos (por ejemplo, modelos fenomenológicos). [7] [ se necesita una mejor fuente ] El modelado ayuda a analizar datos experimentales y abordar preguntas. Los modelos también son importantes en el contexto de la restauración de la funcionalidad cerebral perdida mediante dispositivos neuroprotésicos .
Modelos de voltaje de membrana de entrada-salida eléctrica
Los modelos de esta categoría describen la relación entre las corrientes de membrana neuronal en la etapa de entrada y el voltaje de membrana en la etapa de salida. Esta categoría incluye modelos de integración y disparo (generalizados) y modelos biofísicos inspirados en el trabajo de Hodgkin-Huxley a principios de la década de 1950, que utilizaban una configuración experimental que perforaba la membrana celular y permitía forzar un voltaje/corriente de membrana específico. [8] [9] [10] [11]
La mayoría de las interfaces neuronales eléctricas modernas aplican estimulación eléctrica extracelular para evitar la perforación de la membrana, lo que puede provocar la muerte celular y el daño tisular. Por lo tanto, no está claro hasta qué punto los modelos de neuronas eléctricas son válidos para la estimulación extracelular (véase, por ejemplo, [12] ).
Hodgkin-Huxley
| Propiedad del modelo H&H | Referencias |
|---|---|
| La forma de una espiga individual | [8] [9] [10] [11] |
| La identidad de los iones involucrados | [8] [9] [10] [11] |
| Velocidad de pico a través del axón | [8] |
El modelo de Hodgkin-Huxley (modelo H&H) [8] [9] [10] [11] es un modelo de la relación entre el flujo de corrientes iónicas a través de la membrana celular neuronal y el voltaje de membrana de la célula. [8] [9] [10] [11] Consiste en un conjunto de ecuaciones diferenciales no lineales que describen el comportamiento de los canales iónicos que permean la membrana celular del axón gigante del calamar . Hodgkin y Huxley fueron galardonados con el Premio Nobel de Fisiología o Medicina de 1963 por este trabajo.
Es importante tener en cuenta la relación voltaje-corriente, con múltiples corrientes dependientes del voltaje que cargan la membrana celular con capacidad C m
La ecuación anterior es la derivada temporal de la ley de capacitancia , Q = CV, donde el cambio de la carga total debe explicarse como la suma de las corrientes. Cada corriente está dada por
donde g ( t , V ) es la conductancia o resistencia inversa, que se puede expandir en términos de su conductancia máxima ḡ y las fracciones de activación e inactivación m y h , respectivamente, que determinan cuántos iones pueden fluir a través de los canales de membrana disponibles. Esta expansión está dada por
y nuestras fracciones siguen la cinética de primer orden
con una dinámica similar para h , donde podemos usar τ y m ∞ o α y β para definir nuestras fracciones de puerta.
El modelo de Hodgkin-Huxley puede ampliarse para incluir corrientes iónicas adicionales. Por lo general, estas incluyen corrientes de entrada de Ca 2+ y Na + , así como diversas variedades de corrientes de salida de K + , incluida una corriente de "fuga".
El resultado puede ser un número pequeño de 20 parámetros que se deben estimar o medir para obtener un modelo preciso. En un modelo de un sistema complejo de neuronas, la integración numérica de las ecuaciones es costosa en términos computacionales . Por lo tanto, se necesitan simplificaciones cuidadosas del modelo de Hodgkin-Huxley.
El modelo se puede reducir a dos dimensiones gracias a las relaciones dinámicas que se pueden establecer entre las variables de control. [13] También es posible extenderlo para tener en cuenta la evolución de las concentraciones (consideradas fijas en el modelo original). [14] [15]
Integrar y disparar de forma perfecta
Uno de los primeros modelos de neurona es el modelo de integración y disparo perfecto (también llamado integración y disparo sin fugas), investigado por primera vez en 1907 por Louis Lapicque . [16] Una neurona está representada por su voltaje de membrana V que evoluciona en el tiempo durante la estimulación con una corriente de entrada I(t) de acuerdo con
que es simplemente la derivada temporal de la ley de capacitancia , Q = CV . Cuando se aplica una corriente de entrada, el voltaje de la membrana aumenta con el tiempo hasta que alcanza un umbral constante V th , momento en el que se produce un pico de función delta y el voltaje se restablece a su potencial de reposo, después de lo cual el modelo continúa ejecutándose. La frecuencia de disparo del modelo aumenta linealmente sin límite a medida que aumenta la corriente de entrada.
El modelo se puede hacer más preciso introduciendo un período refractario t ref que limita la frecuencia de disparo de una neurona evitando que se dispare durante ese período. Para una entrada constante I(t)=I, el voltaje umbral se alcanza después de un tiempo de integración t int = CV thr /I después de comenzar desde cero. Después de un reinicio, el período refractario introduce un tiempo muerto de modo que el tiempo total hasta el siguiente disparo es t ref + t int . La frecuencia de disparo es la inversa del intervalo total entre picos (incluido el tiempo muerto). La frecuencia de disparo en función de una corriente de entrada constante es, por lo tanto,
Una deficiencia de este modelo es que no describe ni la adaptación ni la fuga. Si el modelo recibe un pulso de corriente corto por debajo del umbral en algún momento, mantendrá ese aumento de voltaje para siempre, hasta que otra entrada posterior lo haga activarse. Esta característica no está en línea con el comportamiento neuronal observado. Las siguientes extensiones hacen que el modelo de integración y activación sea más plausible desde un punto de vista biológico.
Integración y disparo con fugas
El modelo de integración y disparo con fugas, que se remonta a Louis Lapicque [16] , contiene un término de "fuga" en la ecuación del potencial de membrana que refleja la difusión de iones a través de la membrana, a diferencia del modelo de integración y disparo sin fugas. La ecuación del modelo se ve así: [1]
.jpg/440px-Leaky_Integrate-and-Fire_model_neuron_(schematic).jpg)
donde V m es el voltaje a través de la membrana celular y R m es la resistencia de la membrana. (El modelo de integración y disparo sin fugas se recupera en el límite R m hasta el infinito, es decir, si la membrana es un aislante perfecto). La ecuación del modelo es válida para una entrada arbitraria dependiente del tiempo hasta que se alcanza un umbral V th ; a partir de entonces, se restablece el potencial de membrana.
Para una entrada constante, la entrada mínima para alcanzar el umbral es I th = V th / R m . Suponiendo un restablecimiento a cero, la frecuencia de disparo se ve así:
que converge para grandes corrientes de entrada al modelo anterior sin fugas con el período refractario. [17] El modelo también se puede utilizar para neuronas inhibidoras. [18] [19]
La desventaja más importante de este modelo es que no contiene adaptación neuronal, por lo que no puede describir un tren de picos medido experimentalmente en respuesta a una corriente de entrada constante. [20] Esta desventaja se elimina en modelos generalizados de integración y disparo que también contienen una o varias variables de adaptación y pueden predecir los tiempos de pico de las neuronas corticales bajo inyección de corriente con un alto grado de precisión. [21] [22] [23]
Integración y disparo adaptativos
| Modelo de integración y disparo adaptativo | Referencias |
|---|---|
| Tensión de subumbral para corriente de entrada dependiente del tiempo | [22] [23] |
| Tiempos de disparo para corriente de entrada dependiente del tiempo | [22] [23] |
| Patrones de disparo en respuesta a la entrada de corriente escalonada | [24] [25] [26] |
La adaptación neuronal se refiere al hecho de que incluso en presencia de una inyección de corriente constante en el soma, los intervalos entre los picos de salida aumentan. Un modelo neuronal de integración y disparo adaptativo combina la integración con fugas del voltaje Vcon una o varias variables de adaptación w k (ver Capítulo 6.1. en el libro de texto Dinámica Neuronal [27] )
donde es la constante de tiempo de la membrana, w k es el número de corriente de adaptación, con índice k , es la constante de tiempo de la corriente de adaptación w k , E m es el potencial de reposo y t f es el tiempo de activación de la neurona y la delta griega denota la función delta de Dirac. Siempre que el voltaje alcanza el umbral de activación, el voltaje se restablece a un valor V r por debajo del umbral de activación. El valor de restablecimiento es uno de los parámetros importantes del modelo. El modelo más simple de adaptación tiene solo una única variable de adaptación wy se elimina la suma sobre k. [28]

Las neuronas de integración y disparo con una o varias variables de adaptación pueden explicar una variedad de patrones de disparo neuronal en respuesta a una estimulación constante, incluida la adaptación, el estallido y el estallido inicial. [24] [25] [26] Además, las neuronas de integración y disparo adaptativas con varias variables de adaptación pueden predecir los tiempos de pico de las neuronas corticales bajo una inyección de corriente dependiente del tiempo en el soma. [22] [23]
Integración y disparo con fugas de orden fraccionario
Los recientes avances en el cálculo fraccional teórico y computacional han dado lugar a una nueva forma de modelo denominada integración y disparo con fugas de orden fraccional. [29] [30] Una ventaja de este modelo es que puede capturar los efectos de adaptación con una sola variable. El modelo tiene la siguiente forma: [30]
Una vez que el voltaje alcanza el umbral, se restablece. La integración fraccionaria se ha utilizado para explicar la adaptación neuronal en datos experimentales. [29]
'Integración y disparo exponencial' e 'integración y disparo exponencial adaptativo'
| Integración y disparo exponencial adaptativo | Referencias |
|---|---|
| La relación corriente-voltaje subumbral | [31] |
| Patrones de disparo en respuesta a la entrada de corriente escalonada | [26] |
| Refractariedad y adaptación | [32] |
En el modelo exponencial de integración y disparo , [33] la generación de picos es exponencial, siguiendo la ecuación:
donde es el potencial de membrana, es el umbral del potencial de membrana intrínseco, es la constante de tiempo de membrana, es el potencial de reposo, y es la agudeza del inicio del potencial de acción, usualmente alrededor de 1 mV para neuronas piramidales corticales. [31] Una vez que el potencial de membrana cruza , diverge al infinito en un tiempo finito. [34] En la simulación numérica la integración se detiene si el potencial de membrana alcanza un umbral arbitrario (mucho mayor que ) en el cual el potencial de membrana se restablece a un valor V r . El valor de restablecimiento de voltaje V r es uno de los parámetros importantes del modelo. Es importante destacar que el lado derecho de la ecuación anterior contiene una no linealidad que se puede extraer directamente de los datos experimentales. [31] En este sentido la no linealidad exponencial está fuertemente respaldada por evidencia experimental.
En la neurona exponencial adaptativa de integración y disparo [32], la no linealidad exponencial anterior de la ecuación de voltaje se combina con una variable de adaptación w

donde wIndica la corriente de adaptación con escala de tiempo . Los parámetros importantes del modelo son el valor de restablecimiento de voltaje V r , el umbral intrínseco , las constantes de tiempo y también los parámetros de acoplamiento ay bEl modelo exponencial adaptativo de integración y disparo hereda la no linealidad de voltaje derivada experimentalmente [31] del modelo exponencial de integración y disparo. Pero yendo más allá de este modelo, también puede explicar una variedad de patrones de disparo neuronal en respuesta a la estimulación constante, incluida la adaptación, el estallido y el estallido inicial. [26] Sin embargo, dado que la adaptación se presenta en forma de corriente, puede aparecer una hiperpolarización aberrante. Este problema se resolvió expresándolo como una conductancia. [35]
Modelo adaptativo de neuronas umbral
En este modelo, se añade una función dependiente del tiempo al umbral fijo, , después de cada pico, lo que provoca una adaptación del umbral. El potencial del umbral, , vuelve gradualmente a su valor de estado estable dependiendo de la constante de tiempo de adaptación del umbral . [36] Esta es una de las técnicas más simples para lograr la adaptación de la frecuencia de los picos. [37] La expresión para el umbral adaptativo viene dada por:
donde se define por:
Cuando el potencial de membrana, , alcanza un umbral, se restablece a :
En [38] se realiza una versión más simple de esto con una única constante de tiempo en la caída del umbral con una neurona LIF para lograr redes neuronales de picos recurrentes como LSTM para lograr una precisión más cercana a las ANN en algunas tareas espaciotemporales.
Umbral adaptativo exponencial doble (DEXAT)
El modelo de neurona DEXAT es una variante del modelo de neurona adaptativa en el que el voltaje umbral decae con una exponencial doble que tiene dos constantes de tiempo. La desintegración exponencial doble está regida por una desintegración inicial rápida y luego una desintegración más lenta durante un período de tiempo más largo. [39] [40] Esta neurona utilizada en las redes neuronales segmentarias a través de un gradiente sustituto crea una tasa de aprendizaje adaptativa que produce una mayor precisión y una convergencia más rápida, y una memoria a corto plazo flexible en comparación con las contrapartes existentes en la literatura. La dinámica del potencial de membrana se describe a través de ecuaciones y la regla de adaptación del umbral es:
La dinámica de y está dada por
,
,
donde y .
Además, en [41] se muestra un modelo de neurona umbral adaptativo de escala de tiempo múltiple que muestra una dinámica más compleja.
Modelos estocásticos de voltaje de membrana y tiempo de pico
Los modelos de esta categoría son modelos generalizados de integración y disparo que incluyen un cierto nivel de estocasticidad. En los experimentos, se ha descubierto que las neuronas corticales responden de manera fiable a la entrada dependiente del tiempo, aunque con un pequeño grado de variación entre un ensayo y el siguiente si se repite el mismo estímulo. [42] [43] La estocasticidad en las neuronas tiene dos fuentes importantes. En primer lugar, incluso en un experimento muy controlado en el que se inyecta una corriente de entrada directamente en el soma, los canales iónicos se abren y cierran de manera estocástica [44] y este ruido de canal conduce a una pequeña cantidad de variabilidad en el valor exacto del potencial de membrana y el momento exacto de los picos de salida. En segundo lugar, para una neurona integrada en una red cortical, es difícil controlar la entrada exacta porque la mayoría de las entradas provienen de neuronas no observadas en algún otro lugar del cerebro. [27]
La estocasticidad se ha introducido en los modelos de neuronas en picos en dos formas fundamentalmente diferentes: (i) se agrega una corriente de entrada ruidosa a la ecuación diferencial del modelo de neurona; [45] o (ii) el proceso de generación de picos es ruidoso. [46] En ambos casos, la teoría matemática se puede desarrollar para tiempo continuo, que luego, si se desea para su uso en simulaciones por computadora, se transforma en un modelo de tiempo discreto.
La relación entre el ruido en los modelos neuronales y la variabilidad de los trenes de picos y los códigos neuronales se analiza en Codificación neuronal y en el Capítulo 7 del libro de texto Dinámica neuronal. [27]
Modelo de entrada ruidosa (ruido difusivo)
Una neurona integrada en una red recibe una entrada de picos de otras neuronas. Dado que los tiempos de llegada de los picos no están controlados por un experimentador, se pueden considerar estocásticos. Por lo tanto, un modelo de integración y disparo (potencialmente no lineal) con no linealidad f(v) recibe dos entradas: una entrada controlada por los experimentadores y una corriente de entrada ruidosa que describe la entrada de fondo no controlada.
El modelo de Stein [45] es el caso especial de una neurona con fugas de integración y disparo y una corriente de ruido blanco estacionaria con media cero y varianza unitaria. En el régimen subumbral, estas suposiciones dan como resultado la ecuación del proceso de Ornstein-Uhlenbeck.
Sin embargo, a diferencia del proceso estándar de Ornstein-Uhlenbeck, el voltaje de la membrana se restablece siempre que V alcanza el umbral de disparo V th . [45] El cálculo de la distribución de intervalos del modelo de Ornstein-Uhlenbeck para una entrada constante con umbral conduce a un problema de tiempo de primer paso . [45] [47] El modelo de neurona de Stein y sus variantes se han utilizado para ajustar distribuciones de intervalos entre picos de trenes de picos de neuronas reales bajo una corriente de entrada constante. [47]
En la literatura matemática, la ecuación anterior del proceso Ornstein-Uhlenbeck se escribe en la forma
donde es la amplitud de la entrada de ruido y dW son incrementos de un proceso de Wiener. Para implementaciones de tiempo discreto con paso de tiempo dt las actualizaciones de voltaje son [27]
donde y se extrae de una distribución gaussiana con varianza unitaria media cero. El voltaje se restablece cuando alcanza el umbral de activación V th .
El modelo de entrada ruidosa también se puede utilizar en modelos generalizados de integración y disparo. Por ejemplo, el modelo exponencial de integración y disparo con entrada ruidosa lee
Para una entrada determinista constante es posible calcular la tasa de disparo media como una función de . [48] Esto es importante porque los experimentalistas suelen utilizar la relación frecuencia-corriente (curva fI) para caracterizar una neurona.
La integración y disparo con fugas con entrada ruidosa se ha utilizado ampliamente en el análisis de redes de neuronas con picos. [49] La entrada ruidosa también se denomina "ruido difusivo" porque conduce a una difusión del potencial de membrana subumbral alrededor de la trayectoria libre de ruido (Johannesma, [50] La teoría de las neuronas con picos con entrada ruidosa se analiza en el Capítulo 8.2 del libro de texto Neuronal Dynamics . [27]
Modelo de salida ruidosa (ruido de escape)
En los modelos deterministas de integración y disparo, se genera un pico si el potencial de membrana V (t)alcanza el umbral . En los modelos de salida ruidosos, el umbral estricto se reemplaza por uno ruidoso de la siguiente manera. En cada momento t, se genera un pico de forma estocástica con una intensidad estocástica instantánea o "tasa de escape" [27]
que depende de la diferencia momentánea entre el voltaje de la membrana V (t)y el umbral . [46] Una opción común para la 'tasa de escape' (que es consistente con los datos biológicos [22] ) es
.jpg/440px-Spike_Response_Model_with_escape_noise_(noisy_output).jpg)
donde es una constante de tiempo que describe la rapidez con la que se dispara un pico una vez que el potencial de membrana alcanza el umbral y es un parámetro de nitidez. Porque el umbral se vuelve agudo y el disparo del pico ocurre de manera determinista en el momento en que el potencial de membrana alcanza el umbral desde abajo. El valor de nitidez encontrado en los experimentos [22] es lo que significa que el disparo neuronal se vuelve no despreciable tan pronto como el potencial de membrana está unos pocos mV por debajo del umbral de disparo formal.
El proceso de tasa de escape a través de un umbral suave se analiza en el Capítulo 9 del libro de texto Dinámica neuronal. [27]
Para los modelos en tiempo discreto, se genera un pico con probabilidad
que depende de la diferencia momentánea entre el voltaje de la membrana Ven el tiempo y el umbral . [55] La función F se toma a menudo como una sigmoidea estándar con parámetro de inclinación , [46] similar a la dinámica de actualización en redes neuronales artificiales. Pero la forma funcional de F también se puede derivar de la intensidad estocástica en tiempo continuo introducida anteriormente como donde es la distancia umbral. [46]
Los modelos de integración y disparo con ruido de salida se pueden utilizar para predecir el histograma de tiempo de periestímulo (PSTH) de neuronas reales bajo una entrada arbitraria dependiente del tiempo. [22] Para neuronas de integración y disparo no adaptativas, la distribución de intervalos bajo estimulación constante se puede calcular a partir de la teoría de renovación estacionaria . [27]
Modelo de respuesta a picos (SRM)
| Modelo de respuesta a picos | Referencias |
|---|---|
| Tensión de subumbral para corriente de entrada dependiente del tiempo | [23] [22] |
| Tiempos de disparo para corriente de entrada dependiente del tiempo | [23] [22] |
| Patrones de disparo en respuesta a la entrada de corriente escalonada | [56] [57] |
| Distribución de intervalos entre picos | [56] [46] |
| Potencial de pico posterior | [23] |
| refractariedad y umbral de disparo dinámico | [23] [22] |
Artículo principal : Modelo de respuesta a picos
El modelo de respuesta de pico (SRM) es un modelo lineal generalizado para el voltaje de membrana subumbral combinado con un proceso de ruido de salida no lineal para la generación de picos. [46] [58] [56] El voltaje de membrana V (t)en el momento t es
donde t f es el tiempo de disparo del número de picos f de la neurona, V rest es el voltaje de reposo en ausencia de entrada, I(ts)es la corriente de entrada en el tiempo ts y es un filtro lineal (también llamado kernel) que describe la contribución de un pulso de corriente de entrada en el tiempo ts al voltaje en el tiempo t. Las contribuciones al voltaje causadas por un pico en el tiempo se describen mediante el kernel refractario . En particular, describe el reinicio después del pico y el curso temporal del potencial posterior al pico después de un pico. Por lo tanto, expresa las consecuencias de la refractariedad y la adaptación. [46] [23] El voltaje V(t) se puede interpretar como el resultado de una integración de la ecuación diferencial de un modelo de integración y disparo con fugas acoplado a un número arbitrario de variables de adaptación activadas por picos. [24]
El disparo de picos es estocástico y ocurre con una intensidad estocástica dependiente del tiempo (tasa instantánea)
con parámetros y un umbral dinámico dado por
Aquí se muestra el umbral de activación de una neurona inactiva y se describe el aumento del umbral después de un pico en el tiempo . [22] [23] En el caso de un umbral fijo, se establece . Para el proceso de umbral es determinista. [27]
El curso temporal de los filtros que caracterizan el modelo de respuesta de pico se puede extraer directamente de los datos experimentales. [23] Con parámetros optimizados, el SRM describe el curso temporal del voltaje de membrana subumbral para la entrada dependiente del tiempo con una precisión de 2 mV y puede predecir el tiempo de la mayoría de los picos de salida con una precisión de 4 ms. [22] [23] El SRM está estrechamente relacionado con los modelos de cascada de Poisson lineales-no lineales (también llamados Modelo Lineal Generalizado). [54] La estimación de parámetros de modelos neuronales probabilísticos como el SRM utilizando métodos desarrollados para Modelos Lineales Generalizados [59] se analiza en el Capítulo 10 del libro de texto Neuronal Dynamics . [27]
.jpg/440px-Spike_Response_Model_(schematic).jpg)
El nombre de modelo de respuesta a picos surge porque, en una red, la corriente de entrada para la neurona i es generada por los picos de otras neuronas, de modo que en el caso de una red la ecuación de voltaje se convierte en
donde es el tiempo de disparo de la neurona j (es decir, su tren de picos); describe el curso temporal del pico y el potencial posterior al pico para la neurona i; y describe la amplitud y el curso temporal de un potencial postsináptico excitatorio o inhibidor (PSP) causado por el pico de la neurona presináptica j. El curso temporal del PSP resulta de la convolución de la corriente postsináptica causada por la llegada de un pico presináptico de la neurona j con el filtro de membrana . [27]
SRM0
El SRM 0 [56] [60] [61] es un modelo de neurona estocástica relacionado con la teoría de renovación no lineal dependiente del tiempo y una simplificación del modelo de respuesta a picos (SRM). La principal diferencia con la ecuación de voltaje del SRM presentada anteriormente es que en el término que contiene el núcleo refractario no hay signo de suma sobre los picos pasados: solo importa el pico más reciente (indicado como el tiempo ). Otra diferencia es que el umbral es constante. El modelo SRM0 se puede formular en tiempo discreto o continuo. Por ejemplo, en tiempo continuo, la ecuación de neurona única es
y las ecuaciones de red del SRM 0 son [56]
donde es el último tiempo de disparo de la neurona i. Nótese que también se permite que el curso temporal del potencial postsináptico dependa del tiempo transcurrido desde el último pico de la neurona i para describir un cambio en la conductancia de la membrana durante la refractariedad. [60] La tasa de disparo instantánea (intensidad estocástica) es
donde es un umbral de disparo fijo. Por lo tanto, el disparo de la neurona i depende solo de su entrada y del tiempo transcurrido desde que la neurona i disparó su último pico.
Con el SRM 0 , la distribución de intervalo entre picos para una entrada constante se puede vincular matemáticamente a la forma del núcleo refractario . [46] [56] Además, la relación de frecuencia-corriente estacionaria se puede calcular a partir de la tasa de escape en combinación con el núcleo refractario . [46] [56] Con una elección apropiada de los núcleos, el SRM 0 aproxima la dinámica del modelo de Hodgkin-Huxley a un alto grado de precisión. [60] Además, se puede predecir la respuesta del PSTH a una entrada arbitraria dependiente del tiempo. [56]
Modelo de Galves-Löcherbach

El modelo de Galves-Löcherbach [62] es un modelo de neurona estocástica estrechamente relacionado con el modelo de respuesta a picos SRM 0 [61] [56] y el modelo de integración y disparo con fugas. Es inherentemente estocástico y, al igual que el SRM 0 , está vinculado a la teoría de renovación no lineal dependiente del tiempo . Dadas las especificaciones del modelo, la probabilidad de que una neurona dada presente picos en un período puede describirse mediante
donde es un peso sináptico , que describe la influencia de la neurona en la neurona , expresa la fuga y proporciona el historial de picos de la neurona antes , según
Es importante destacar que la probabilidad de pico de una neurona depende únicamente de su pico de entrada (filtrado con un kernel y ponderado con un factor ) y del momento de su pico de salida más reciente (resumido por ).
Modelos didácticos de juguetes de voltaje de membrana.
Los modelos de esta categoría son modelos de juguete altamente simplificados que describen cualitativamente el voltaje de la membrana en función de la entrada. Se utilizan principalmente por razones didácticas en la enseñanza, pero no se consideran modelos neuronales válidos para simulaciones a gran escala o para el ajuste de datos.
FitzHugh–Nagumo
FitzHugh y Nagumo introdujeron simplificaciones radicales de Hodgkin-Huxley en 1961 y 1962. Buscando describir la "autoexcitación regenerativa" mediante un voltaje de membrana de retroalimentación positiva no lineal y la recuperación mediante un voltaje de compuerta de retroalimentación negativa lineal, desarrollaron el modelo descrito por [63]
donde nuevamente tenemos un voltaje y una corriente de entrada similares a los de una membrana con un voltaje de compuerta general más lento w y parámetros determinados experimentalmente a = -0,7, b = 0,8, τ = 1/0,08 . Aunque no se puede derivar de la biología, el modelo permite una dinámica simplificada e inmediatamente disponible, sin ser una simplificación trivial. [64] El apoyo experimental es débil, pero el modelo es útil como herramienta didáctica para introducir la dinámica de la generación de picos a través del análisis del plano de fase . Véase el Capítulo 7 del libro de texto Métodos de modelado neuronal . [65]
Morris-Lecar
En 1981, Morris y Lecar combinaron los modelos de Hodgkin-Huxley y FitzHugh-Nagumo en un modelo de canal de calcio dependiente de voltaje con un canal de potasio rectificador retardado representado por
donde . [17] El soporte experimental del modelo es débil, pero el modelo es útil como herramienta didáctica para introducir la dinámica de la generación de picos a través del análisis del plano de fase . Véase el Capítulo 7 [66] en el libro de texto Métodos de modelado neuronal . [65]
Se puede derivar paso a paso un modelo de neurona bidimensional muy similar al modelo de Morris-Lecar a partir del modelo de Hodgkin-Huxley. Véase el capítulo 4.2 del libro de texto Neuronal Dynamics. [27]
Marisma Hindmarsh-Rose
Basándose en el modelo de FitzHugh-Nagumo, Hindmarsh y Rose propusieron en 1984 [67] un modelo de actividad neuronal descrito por tres ecuaciones diferenciales de primer orden acopladas:
con r 2 = x 2 + y 2 + z 2 , y r ≈ 10 −2 de modo que la variable z solo cambia muy lentamente. Esta complejidad matemática adicional permite una gran variedad de comportamientos dinámicos para el potencial de membrana, descrito por la variable x del modelo, que incluye dinámica caótica. Esto hace que el modelo de neurona de Hindmarsh-Rose sea muy útil, porque sigue siendo simple y permite una buena descripción cualitativa de los muchos patrones de disparo diferentes del potencial de acción, en particular el estallido, observado en experimentos. Sin embargo, sigue siendo un modelo de juguete y no se ha ajustado a los datos experimentales. Se usa ampliamente como modelo de referencia para la dinámica del estallido. [67]
Modelo theta y función de integración y disparo cuadrático
El modelo theta , o modelo canónico de tipo I de Ermentrout-Kopell, es matemáticamente equivalente al modelo cuadrático de integración y disparo, que a su vez es una aproximación al modelo exponencial de integración y disparo y al modelo de Hodgkin-Huxley. Se denomina modelo canónico porque es uno de los modelos genéricos para entradas constantes cercanas al punto de bifurcación, lo que significa cerca de la transición de disparo silencioso a disparo repetitivo. [68] [69]
La formulación estándar del modelo theta es [27] [68] [69]
La ecuación para el modelo cuadrático de integración y disparo es (ver Capítulo 5.3 en el libro de texto Neuronal Dynamics [27] )
La equivalencia del modelo theta y la integración y disparo cuadráticos se analiza, por ejemplo, en el Capítulo 4.1.2.2 de modelos de neuronas en pico. [1]
Para entradas que cambian con el tiempo o están lejos del punto de bifurcación, es preferible trabajar con el modelo exponencial de integración y disparo (si uno quiere permanecer en la clase de modelos de neuronas unidimensionales), porque las neuronas reales exhiben la no linealidad del modelo exponencial de integración y disparo. [31]
Modelos de neuronas codificadoras de estímulos de entrada sensorial
Los modelos de esta categoría se derivaron de experimentos que involucraban estimulación natural, como luz, sonido, tacto u olor. En estos experimentos, el patrón de picos resultante de la presentación de cada estímulo varía de un ensayo a otro, pero la respuesta promedio de varios ensayos a menudo converge hacia un patrón claro. En consecuencia, los modelos de esta categoría generan una relación probabilística entre el estímulo de entrada y la ocurrencia de picos. Es importante destacar que las neuronas registradas a menudo se ubican varios pasos de procesamiento después de las neuronas sensoriales, de modo que estos modelos resumen los efectos de la secuencia de pasos de procesamiento en una forma compacta.
El modelo de proceso de Poisson no homogéneo (Siebert)
Siebert [70] [71] modeló el patrón de disparo de picos de neuronas utilizando un modelo de proceso de Poisson no homogéneo , siguiendo experimentos que involucraban al sistema auditivo. [70] [71] Según Siebert, la probabilidad de un evento de pico en el intervalo de tiempo es proporcional a una función no negativa , donde es el estímulo bruto.:
Siebert consideró varias funciones como , incluso para intensidades de estímulo bajas.
La principal ventaja del modelo de Siebert es su simplicidad. El inconveniente del modelo es su incapacidad para reflejar adecuadamente los siguientes fenómenos:
- El aumento transitorio de la actividad de disparo neuronal en respuesta a un estímulo escalonado.
- La saturación de la velocidad de disparo.
- Los valores del histograma de intervalo entre picos son valores de intervalos cortos (cercanos a cero).
Estas deficiencias se abordan mediante el modelo de proceso puntual dependiente de la edad y el modelo de Markov de dos estados. [72] [73] [74]
Modelo de proceso puntual dependiente de la edad y refractariedad
Berry y Meister [75] estudiaron la refractariedad neuronal utilizando un modelo estocástico que predice picos como un producto de dos términos, una función f(s(t)) que depende del estímulo dependiente del tiempo s(t) y una función de recuperación que depende del tiempo desde el último pico.
El modelo también se denomina proceso de intervalo de Markov no homogéneo (IMI) . [76] Se han utilizado modelos similares durante muchos años en la neurociencia auditiva. [77] [78] [79] Dado que el modelo mantiene la memoria del último momento de pico, no es Poisson y cae en la clase de modelos de renovación dependientes del tiempo. [27] Está estrechamente relacionado con el modelo SRM0 con tasa de escape exponencial. [27] Es importante destacar que es posible ajustar los parámetros del modelo de proceso puntual dependiente de la edad para describir no solo la respuesta PSTH, sino también las estadísticas de intervalo entre picos. [76] [77] [79]
Modelo de cascada de Poisson lineal-no lineal y GLM
El modelo de cascada de Poisson lineal-no lineal es una cascada de un proceso de filtrado lineal seguido de un paso de generación de picos no lineal. [80] En el caso de que los picos de salida se retroalimenten, a través de un proceso de filtrado lineal, llegamos a un modelo que se conoce en las neurociencias como Modelo Lineal Generalizado (GLM). [54] [59] El GLM es matemáticamente equivalente al modelo de respuesta a picos (SRM) con ruido de escape; pero mientras que en el SRM las variables internas se interpretan como el potencial de membrana y el umbral de disparo, en el GLM las variables internas son cantidades abstractas que resumen el efecto neto de la entrada (y los picos de salida recientes) antes de que se generen los picos en el paso final. [27] [54]
El modelo de Markov de dos estados (Nossenson y Messer)
El modelo de neurona de activación de Nossenson y Messer [72] [73] [74] produce la probabilidad de que la neurona active una activación como una función de un estímulo externo o farmacológico. [72] [73] [74] El modelo consiste en una cascada de un modelo de capa receptora y un modelo de neurona de activación, como se muestra en la Figura 4. La conexión entre el estímulo externo y la probabilidad de activación se realiza en dos pasos: primero, un modelo de célula receptora traduce el estímulo externo en bruto a concentración de neurotransmisores y, luego, un modelo de neurona de activación conecta la concentración de neurotransmisores con la tasa de activación (probabilidad de activación). Por lo tanto, el modelo de neurona de activación por sí mismo depende de la concentración de neurotransmisores en la etapa de entrada. [72] [73] [74]


Una característica importante de este modelo es la predicción del patrón de frecuencia de disparo de las neuronas, que captura, utilizando un número reducido de parámetros libres, la respuesta característica de las neuronas enfatizada en los bordes a un pulso de estímulo, como se muestra en la figura 5. La frecuencia de disparo se identifica tanto como una probabilidad normalizada de disparo de picos neuronales como una cantidad proporcional a la corriente de neurotransmisores liberados por la célula. La expresión para la frecuencia de disparo adopta la siguiente forma:
dónde,
- P0 es la probabilidad de que la neurona esté "armada" y lista para disparar. Se obtiene mediante la siguiente ecuación diferencial:
P0 se puede calcular de forma recursiva utilizando el método de Euler, pero en el caso de un pulso de estímulo, produce una expresión simple de forma cerrada. [72] [81]
- y ( t ) es la entrada del modelo y se interpreta como la concentración de neurotransmisores en el entorno celular (en la mayoría de los casos, glutamato). Para un estímulo externo, se puede estimar a través del modelo de la capa receptora:
siendo un promedio temporal corto de la potencia del estímulo (expresado en vatios u otra energía por unidad de tiempo).
- R 0 corresponde a la tasa de disparo espontáneo intrínseco de la neurona.
- R 1 es la tasa de recuperación de la neurona del estado refractario.
Otras predicciones de este modelo incluyen:
1) El potencial de respuesta evocada (PRE) promedio debido a la población de muchas neuronas en mediciones sin filtrar se asemeja a la tasa de disparo. [74]
2) La variación de voltaje de la actividad debido a la actividad neuronal múltiple se asemeja a la tasa de activación (también conocida como potencia de actividad de unidades múltiples o MUA). [73] [74]
3) La distribución de probabilidad entre intervalos de picos toma la forma de una función similar a una distribución gamma. [72] [81]
| Propiedad del modelo de Nossenson & Messer | Referencias | Descripción de la evidencia experimental |
|---|---|---|
| La forma de la frecuencia de disparo en respuesta a un pulso de estímulo auditivo. | [82] [83] [84] [85] [86] | La velocidad de disparo tiene la misma forma que la figura 5. |
| La forma de la frecuencia de disparo en respuesta a un pulso de estímulo visual. | [87] [88] [89] [90] | La velocidad de disparo tiene la misma forma que la figura 5. |
| La forma de la frecuencia de disparo en respuesta a un pulso de estímulo olfativo. | [91] | La velocidad de disparo tiene la misma forma que la figura 5. |
| La forma de la frecuencia de disparo en respuesta a un estímulo somatosensorial | [92] | La velocidad de disparo tiene la misma forma que la figura 5. |
| El cambio en la tasa de activación en respuesta a la aplicación de neurotransmisores (principalmente glutamato) | [93] [94] | Cambio de la tasa de activación en respuesta a la aplicación de neurotransmisores (glutamato) |
| Dependencia cuadrada entre la presión de un estímulo auditivo y la frecuencia de disparo | [95] | Dependencia cuadrada entre la presión del estímulo auditivo y la frecuencia de disparo (- Dependencia lineal en el cuadrado de la presión (potencia)). |
| Dependencia cuadrada entre el campo eléctrico del estímulo visual (voltios) y la frecuencia de disparo | [88] | Dependencia cuadrada entre el campo eléctrico del estímulo visual (voltios) - Dependencia lineal entre la potencia del estímulo visual y la frecuencia de disparo. |
| La forma de las estadísticas de intervalo entre picos (ISI) | [96] | La forma de ISI se asemeja a la función gamma. |
| El ERP se asemeja a la tasa de disparo en mediciones sin filtrar | [97] | La forma del potencial de respuesta evocado promedio en respuesta al estímulo se asemeja a la tasa de disparo (Fig. 5). |
| La potencia de MUA se asemeja a la velocidad de disparo | [74] [98] | La forma de la varianza empírica de las mediciones extracelulares en respuesta al pulso de estímulo se asemeja a la tasa de disparo (Fig. 5). |
Modelos de neuronas de estímulo de entrada farmacológica
Los modelos de esta categoría producen predicciones para experimentos que involucran estimulación farmacológica.
Transmisión sináptica (Koch y Segev)
Según el modelo de Koch y Segev, [17] la respuesta de una neurona a neurotransmisores individuales puede modelarse como una extensión del modelo clásico de Hodgkin-Huxley con corrientes cinéticas estándar y no estándar. Cuatro neurotransmisores influyen principalmente en el SNC. Los receptores AMPA/kainato son mediadores excitatorios rápidos, mientras que los receptores NMDA median corrientes considerablemente más lentas. Las corrientes inhibitorias rápidas pasan por los receptores GABA A , mientras que los receptores GABA B median por canales de potasio secundarios activados por proteína G. Este rango de mediación produce la siguiente dinámica de corriente:
donde ḡ es la conductancia máxima [8] [17] (alrededor de 1 S ) y E es el potencial de equilibrio del ion o transmisor dado (AMDA, NMDA, Cl o K ), mientras que [ O ] describe la fracción de receptores abiertos. Para NMDA, hay un efecto significativo del bloqueo de magnesio que depende sigmoideamente de la concentración de magnesio intracelular por B ( V ) . Para GABA B , [ G ] es la concentración de la proteína G y K d describe la disociación de G en la unión a las compuertas de potasio.
La dinámica de este modelo más complicado ha sido bien estudiada experimentalmente y produce resultados importantes en términos de potenciación y depresión sináptica muy rápida , es decir, aprendizaje rápido y de corto plazo.
El modelo estocástico de Nossenson y Messer traduce la concentración de neurotransmisores en la etapa de entrada a la probabilidad de liberar neurotransmisores en la etapa de salida. [72] [73] [74] Para una descripción más detallada de este modelo, consulte la sección Modelo de Markov de dos estados más arriba.
Modelo de neuronas HTM
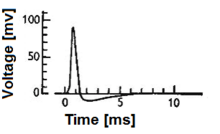
El modelo de neuronas HTM fue desarrollado por Jeff Hawkins e investigadores de Numenta y se basa en una teoría llamada Memoria temporal jerárquica , descrita originalmente en el libro Sobre la inteligencia . Se basa en la neurociencia y en la fisiología e interacción de las neuronas piramidales en el neocórtex del cerebro humano.
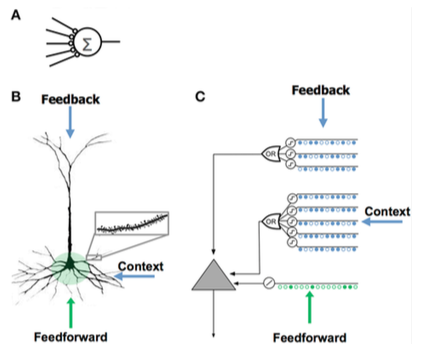
Red neuronal artificial (RNA) | Neurona piramidal neocortical (neurona biológica) | Modelo HTM de neurona |
| - Pocas sinapsis - Sin dendritas - Suma de entradas x pesos - Aprende modificando los pesos de las sinapsis. | - Miles de sinapsis en las dendritas - Dendritas activas: la célula reconoce cientos de patrones únicos - La coactivación de un conjunto de sinapsis en un segmento dendrítico provoca un pico de NMDA y una despolarización en el soma. - Fuentes de entrada a la célula:
- Aprende creando nuevas sinapsis. | - Inspirado en las células piramidales de las capas 2/3 y 5 del neocórtex. - Miles de sinapsis - Dendritas activas: la célula reconoce cientos de patrones únicos - Modela dendritas y picos NMDA con cada matriz de detectores coincidentes que tienen un conjunto de sinapsis - Aprende modelando el crecimiento de nuevas sinapsis. |
Aplicaciones
Los modelos de neuronas en pico se utilizan en una variedad de aplicaciones que necesitan codificación o decodificación de trenes de picos neuronales en el contexto de neuroprótesis e interfaces cerebro-computadora como prótesis de retina : [12] [99] [100] [101] o control y sensación de miembros artificiales. [102] [103] [104] Las aplicaciones no son parte de este artículo; para obtener más información sobre este tema, consulte el artículo principal.
Relación entre modelos de neuronas artificiales y biológicas
El modelo más básico de una neurona consiste en una entrada con un vector de peso sináptico y una función de activación o función de transferencia dentro de la neurona que determina la salida. Esta es la estructura básica que se utiliza para las neuronas artificiales, que en una red neuronal a menudo se ven así:
donde y i es la salida de la neurona i , x j es la señal de entrada de la neurona j , w ij es el peso sináptico (o fuerza de conexión) entre las neuronas i y j , y φ es la función de activación . Si bien este modelo ha tenido éxito en aplicaciones de aprendizaje automático, es un modelo deficiente para neuronas reales (biológicas), porque carece de dependencia del tiempo en la entrada y la salida.
Cuando se activa una entrada en un momento t y se mantiene constante a partir de entonces, las neuronas biológicas emiten un tren de impulsos. Es importante destacar que este tren de impulsos no es regular, sino que presenta una estructura temporal caracterizada por la adaptación, la ráfaga o la ráfaga inicial seguida de impulsos regulares. Los modelos generalizados de integración y disparo, como el modelo de integración y disparo exponencial adaptativo, el modelo de respuesta a los impulsos o el modelo de integración y disparo adaptativo (lineal) pueden capturar estos patrones de disparo neuronal. [24] [25] [26]
Además, la entrada neuronal en el cerebro depende del tiempo. La entrada dependiente del tiempo se transforma mediante filtros lineales y no lineales complejos en un tren de picos en la salida. Nuevamente, el modelo de respuesta a picos o el modelo de integración y disparo adaptativo permite predecir el tren de picos en la salida para una entrada arbitraria dependiente del tiempo, [22] [23] mientras que una neurona artificial o un simple modelo de integración y disparo con fugas no lo hacen.
Si tomamos el modelo de Hodgkin-Huxley como punto de partida, se pueden derivar sistemáticamente modelos generalizados de integración y disparo mediante un procedimiento de simplificación paso a paso. Esto se ha demostrado explícitamente para el modelo exponencial de integración y disparo [33] y el modelo de respuesta de pico [60] .
En el caso de modelar una neurona biológica, se utilizan análogos físicos en lugar de abstracciones como "peso" y "función de transferencia". Una neurona está llena y rodeada de iones que contienen agua, que llevan carga eléctrica. La neurona está unida por una membrana celular aislante y puede mantener una concentración de iones cargados en cada lado que determina una capacitancia C m . La activación de una neurona implica el movimiento de iones hacia la célula, que ocurre cuando los neurotransmisores hacen que se abran los canales iónicos en la membrana celular. Describimos esto mediante una corriente física dependiente del tiempo I ( t ) . Con esto viene un cambio en el voltaje , o la diferencia de energía potencial eléctrica entre la célula y sus alrededores, que se observa que a veces da como resultado un pico de voltaje llamado potencial de acción que viaja a lo largo de la célula y desencadena la liberación de más neurotransmisores. El voltaje, entonces, es la cantidad de interés y está dada por V m ( t ) . [19]
Si la corriente de entrada es constante, la mayoría de las neuronas emiten, después de un tiempo de adaptación o de una descarga inicial, un tren de impulsos regular. La frecuencia de descarga regular en respuesta a una corriente constante I se describe mediante la relación frecuencia-corriente, que corresponde a la función de transferencia de las redes neuronales artificiales. De manera similar, para todos los modelos de neuronas con impulsos, la función de transferencia se puede calcular numéricamente (o analíticamente).
Teoría de cables y modelos compartimentados
Todos los modelos deterministas anteriores son modelos de neuronas puntuales porque no consideran la estructura espacial de una neurona. Sin embargo, la dendrita contribuye a transformar la entrada en salida. [105] [65] Los modelos de neuronas puntuales son una descripción válida en tres casos. (i) Si la corriente de entrada se inyecta directamente en el soma. (ii) Si la entrada sináptica llega predominantemente al soma o cerca de él (la proximidad se define mediante una escala de longitud que se presenta a continuación. (iii) Si la sinapsis llega a cualquier parte de la dendrita, pero la dendrita es completamente lineal. En el último caso, el cable actúa como un filtro lineal; estas propiedades de filtro lineal se pueden incluir en la formulación de modelos generalizados de integración y disparo, como el modelo de respuesta a picos .
Las propiedades del filtro se pueden calcular a partir de una ecuación de cable .
Consideremos una membrana celular en forma de cable cilíndrico. La posición en el cable se denota por x y el voltaje a través de la membrana celular por V. El cable se caracteriza por una resistencia longitudinal por unidad de longitud y una resistencia de membrana . Si todo es lineal, el voltaje cambia en función del tiempo.
| ( 19 ) |
Introducimos una escala de longitud en el lado izquierdo y una constante de tiempo en el lado derecho. La ecuación del cable ahora puede escribirse en su forma quizás más conocida:
| ( 20 ) |
La ecuación de cable anterior es válida para un solo cable cilíndrico.
La teoría del cable lineal describe el árbol dendrítico de una neurona como una estructura cilíndrica que experimenta un patrón regular de bifurcación , como las ramas de un árbol. Para un solo cilindro o un árbol entero, la conductancia de entrada estática en la base (donde el árbol se encuentra con el cuerpo celular o cualquier límite similar) se define como
- ,
donde L es la longitud electrotónica del cilindro, que depende de su longitud, diámetro y resistencia. Un algoritmo recursivo simple escala linealmente con el número de ramas y se puede utilizar para calcular la conductancia efectiva del árbol. Esto viene dado por
donde A D = πld es la superficie total del árbol de longitud total l , y L D es su longitud electrotónica total. Para una neurona entera en la que la conductancia del cuerpo celular es G S y la conductancia de la membrana por unidad de área es G md = G m / A , encontramos la conductancia neuronal total G N para n árboles dendríticos sumando todas las conductancias del árbol y del soma, dadas por
donde podemos encontrar el factor de corrección general F dga experimentalmente observando G D = G md A D F dga .
El modelo de cable lineal realiza varias simplificaciones para dar resultados analíticos cerrados, a saber, que el árbol dendrítico debe ramificarse en pares decrecientes en un patrón fijo y que las dendritas son lineales. Un modelo compartimental [65] permite cualquier topología de árbol deseada con ramas y longitudes arbitrarias, así como no linealidades arbitrarias. Es esencialmente una implementación computacional discretizada de dendritas no lineales.
Cada pieza o compartimento de una dendrita está modelada por un cilindro recto de longitud arbitraria l y diámetro d que se conecta con una resistencia fija a cualquier número de cilindros ramificados. Definimos la relación de conductancia del i- ésimo cilindro como B i = G i / G ∞ , donde y R i es la resistencia entre el compartimento de corriente y el siguiente. Obtenemos una serie de ecuaciones para las relaciones de conductancia dentro y fuera de un compartimento haciendo correcciones a la dinámica normal B out, i = B in, i+1 , como
donde la última ecuación se ocupa de los padres y las hijas en las ramas, y . Podemos iterar estas ecuaciones a través del árbol hasta que lleguemos al punto donde las dendritas se conectan al cuerpo celular (soma), donde la relación de conductancia es B in,stem . Entonces nuestra conductancia neuronal total para la entrada estática está dada por
Es importante destacar que la entrada estática es un caso muy especial. En biología, las entradas dependen del tiempo. Además, las dendritas no siempre son lineales.
Los modelos compartimentados permiten incluir no linealidades a través de canales iónicos ubicados en ubicaciones arbitrarias a lo largo de las dendritas. [105] [106] Para entradas estáticas, a veces es posible reducir la cantidad de compartimentos (aumentar la velocidad computacional) y aún así conservar las características eléctricas salientes. [107]
Conjeturas sobre el papel de la neurona en el contexto más amplio del principio de funcionamiento del cerebro
El esquema de detección de energía basado en neurotransmisores
El esquema de detección de energía basado en neurotransmisores [74] [81] sugiere que el tejido neural ejecuta químicamente un procedimiento de detección similar al radar.

Como se muestra en la figura 6, la idea clave de la conjetura es tener en cuenta la concentración de neurotransmisores, la generación de neurotransmisores y las tasas de eliminación de neurotransmisores como las cantidades importantes en la ejecución de la tarea de detección, al tiempo que se hace referencia a los potenciales eléctricos medidos como un efecto secundario que solo en ciertas condiciones coincide con el propósito funcional de cada paso. El esquema de detección es similar a una "detección de energía" tipo radar porque incluye la cuadratura de la señal, la suma temporal y un mecanismo de conmutación de umbral, al igual que el detector de energía, pero también incluye una unidad que enfatiza los bordes del estímulo y una longitud de memoria variable (memoria variable). Según esta conjetura, el equivalente fisiológico de las estadísticas de la prueba de energía es la concentración de neurotransmisores, y la tasa de activación corresponde a la corriente de neurotransmisores. La ventaja de esta interpretación es que conduce a una explicación coherente con la unidad que permite un puente entre las mediciones electrofisiológicas, las mediciones bioquímicas y los resultados psicofísicos.
La evidencia revisada en [74] [81] sugiere la siguiente asociación entre la funcionalidad y la clasificación histológica:
- Es probable que la cuadratura del estímulo la realicen las células receptoras.
- El énfasis del borde del estímulo y la transducción de señales lo realizan las neuronas.
- La acumulación temporal de neurotransmisores la realizan las células gliales. Es probable que también se produzca una acumulación a corto plazo de neurotransmisores en algunos tipos de neuronas.
- Las células gliales realizan cambios lógicos que resultan de superar un nivel umbral de concentración de neurotransmisores. Este cruce del umbral también va acompañado de un cambio en la tasa de fuga de neurotransmisores.
- El cambio de movimiento físico total o nulo se debe a las células musculares y es resultado de superar un cierto umbral de concentración de neurotransmisores en el entorno muscular.
Cabe señalar que, si bien las señales electrofisiológicas de la figura 6 suelen ser similares a la señal funcional (potencia de la señal/concentración de neurotransmisores/fuerza muscular), existen algunas etapas en las que la observación eléctrica difiere del propósito funcional del paso correspondiente. En particular, Nossenson et al. sugirieron que el cruce del umbral de la glía tiene una operación funcional completamente diferente en comparación con la señal electrofisiológica irradiada y que esta última podría ser solo un efecto secundario de la rotura de la glía.
Comentarios generales sobre la perspectiva moderna de los modelos científicos y de ingeniería
- Los modelos anteriores son todavía idealizaciones. Deben hacerse correcciones por el aumento de la superficie de la membrana debido a numerosas espinas dendríticas, temperaturas significativamente más altas que los datos experimentales a temperatura ambiente y la falta de uniformidad en la estructura interna de la célula. [17] Ciertos efectos observados no encajan en algunos de estos modelos. Por ejemplo, el ciclo de temperatura (con un aumento neto mínimo de la temperatura) de la membrana celular durante la propagación del potencial de acción no es compatible con los modelos que se basan en modelar la membrana como una resistencia que debe disipar energía cuando la corriente fluye a través de ella. El engrosamiento transitorio de la membrana celular durante la propagación del potencial de acción tampoco es predicho por estos modelos, ni tampoco se incorporan a estos modelos la capacitancia cambiante y el pico de voltaje que resulta de este engrosamiento. La acción de algunos anestésicos como los gases inertes también es problemática para estos modelos. Nuevos modelos, como el modelo solitón, intentan explicar estos fenómenos, pero están menos desarrollados que los modelos más antiguos y aún no se han aplicado ampliamente.
- Las opiniones modernas sobre el papel del modelo científico sugieren que "todos los modelos son erróneos, pero algunos son útiles" (Box y Draper, 1987, Gribbin, 2009; Paninski et al., 2009).
- Una conjetura reciente sugiere que cada neurona podría funcionar como una colección de unidades de umbral independientes. Se sugiere que una neurona podría activarse anisotrópicamente siguiendo el origen de sus señales que llegan a la membrana, a través de sus árboles dendríticos. También se propuso que la forma de onda de la punta dependía del origen del estímulo. [108]
Enlaces externos
- Dinámica neuronal: de neuronas individuales a redes y modelos de cognición (W. Gerstner, W. Kistler, R. Naud, L. Paninski, Cambridge University Press, 2014) . [27] En particular, los capítulos 6 a 10, versión en línea html.
- Modelos de neuronas activas [1] (W. Gerstner y W. Kistler, Cambridge University Press, 2002)
Véase también
- Neurona de enlace
- Enfoques bayesianos de la función cerebral
- Interfaces cerebro-computadora
- Principio de energía libre
- Modelos de computación neuronal
- Codificación neuronal
- Oscilación neuronal
- Modelos cuantitativos del potencial de acción
- Red neuronal con picos
Referencias
- ^ abcd Gerstner W, Kistler WM (2002). Modelos de neuronas en pico: neuronas individuales, poblaciones, plasticidad. Cambridge, Reino Unido: Cambridge University Press. ISBN 0-511-07817-X.OCLC 57417395 .
- ^ DeFelipe, Javier; Farinas, Isabel (1992). "La neurona piramidal de la corteza cerebral: características morfológicas y químicas de las entradas sinápticas". Progreso en Neurobiología . 39 (6): 563–607. doi :10.1016/0301-0082(92)90015-7. PMID 1410442. S2CID 34889543.
- ^ Markram, Henry; Muller, Eilif; Ramaswamy, Srikanth; Reimann, Michael; Abdellah, Marwan (2015). "Reconstrucción y simulación de microcircuitos neocorticales". Cell . 163 (2): 456–492. doi : 10.1016/j.cell.2015.09.029 . PMID 26451489. S2CID 14466831.
- ^ Wong, RKS; Traub, RD (1 de enero de 2009), "REDES | Propiedades celulares y conectividad sináptica de las células piramidales CA3: mecanismos de sincronización epiléptica y epileptogénesis", en Schwartzkroin, Philip A. (ed.), Encyclopedia of Basic Epilepsy Research , Oxford: Academic Press, págs. 815–819, doi :10.1016/b978-012373961-2.00215-0, ISBN 978-0-12-373961-2, consultado el 18 de noviembre de 2020
- ^ Lapicque, LM (1907). "Búsquedas cuantitativas sobre la excitación eléctrica de los nerfs". J Physiol París . 9 : 620–635.
- ^ Abbott, Larry (1999). "Introducción de Lapicque del modelo de neurona de integración y disparo (1907)". Boletín de investigación cerebral . 50 (5): 303–304. doi :10.1016/S0361-9230(99)00161-6. PMID 10643408. S2CID 46170924.
- ^ Gauld, Christophe; Brun, Cédric; Boraud, Thomas; Carlu, Mallory; Depannemaecker, Damien (14 de enero de 2022). "Modelos computacionales en neurociencias entre caracterizaciones mecanicistas y fenomenológicas". doi : 10.20944/preprints202201.0206.v1 . S2CID 246059455.
- ^ abcdefg Hodgkin AL, Huxley AF (agosto de 1952). "Una descripción cuantitativa de la corriente de membrana y su aplicación a la conducción y excitación en el nervio". The Journal of Physiology . 117 (4): 500–44. doi :10.1113/jphysiol.1952.sp004764. PMC 1392413 . PMID 12991237.
- ^ abcde Hodgkin AL, Huxley AF, Katz B (abril de 1952). "Medición de las relaciones corriente-voltaje en la membrana del axón gigante de Loligo". The Journal of Physiology . 116 (4): 424–48. doi :10.1113/jphysiol.1952.sp004716. PMC 1392219 . PMID 14946712.
- ^ abcde Hodgkin AL, Huxley AF (abril de 1952). "Corrientes transportadas por iones de sodio y potasio a través de la membrana del axón gigante de Loligo". The Journal of Physiology . 116 (4): 449–72. doi :10.1113/jphysiol.1952.sp004717. PMC 1392213 . PMID 14946713.
- ^ abcde Hodgkin AL, Huxley AF (abril de 1952). "Los componentes de la conductancia de la membrana en el axón gigante de Loligo". The Journal of Physiology . 116 (4): 473–96. doi :10.1113/jphysiol.1952.sp004718. PMC 1392209 . PMID 14946714.
- ^ ab Mathieson K, Loudin J, Goetz G, Huie P, Wang L, Kamins TI, et al. (junio de 2012). "Prótesis de retina fotovoltaica con alta densidad de píxeles". Nature Photonics . 6 (6): 391–397. Bibcode :2012NaPho...6..391M. doi :10.1038/nphoton.2012.104. PMC 3462820 . PMID 23049619.
- ^ Izhikevich EM (2010). Sistemas dinámicos en neurociencia: la geometría de la excitabilidad y la explosión . Cambridge, MA: MIT Press. ISBN 978-0-262-51420-0.OCLC 457159828 .
- ^ Cressman JR, Ullah G, Ziburkus J, Schiff SJ, Barreto E (abril de 2009). "La influencia de la dinámica del sodio y el potasio en la excitabilidad, las convulsiones y la estabilidad de los estados persistentes: I. Dinámica de neuronas individuales". Journal of Computational Neuroscience . 26 (2): 159–70. doi :10.1007/s10827-008-0132-4. PMC 2704057 . PMID 19169801.
- ^ Depannemaecker D, Ivanov A, Lillo D, Spek L, Bernard C, Jirsa V (17 de febrero de 2021). "Un marco fisiológico unificado de transiciones entre convulsiones, actividad ictal sostenida y bloqueo de despolarización a nivel de neurona única". bioRxiv : 2020.10.23.352021. doi : 10.1101/2020.10.23.352021 . S2CID 225962412.
- ^ ab Abbott LF (1999). "La introducción de Lapicque del modelo de neurona de integración y disparo (1907)" (PDF) . Brain Research Bulletin . 50 (5–6): 303–4. doi :10.1016/S0361-9230(99)00161-6. PMID 10643408. S2CID 46170924. Archivado desde el original (PDF) el 2007-06-13.
- ^ abcde Koch C, Segev I (1999). Métodos de modelado neuronal: de iones a redes (2.ª ed.). Cambridge, Massachusetts: MIT Press. pág. 687. ISBN 978-0-262-11231-4Archivado desde el original el 7 de julio de 2011. Consultado el 10 de enero de 2013 .
- ^ Brunel N (1 de mayo de 2000). "Dinámica de redes escasamente conectadas de neuronas excitadoras e inhibidoras". Journal of Computational Neuroscience . 8 (3): 183–208. doi :10.1023/A:1008925309027. PMID 10809012. S2CID 1849650.
- ^ ab Cejnar P, Vyšata O, Kukal J, Beránek M, Vališ M, Procházka A (abril de 2020). "Un modelo simple de interruptor de condensador de neurona excitatoria e inhibidora con todas las partes explicadas biológicamente permite oscilaciones caóticas dependientes del patrón de disparo de entrada". Scientific Reports . 10 (1): 7353. Bibcode :2020NatSR..10.7353C. doi :10.1038/s41598-020-63834-7. PMC 7192907 . PMID 32355185.
- ^ Fuortes MG, Mantegazzini F (julio de 1962). "Interpretación de la activación repetitiva de las células nerviosas". The Journal of General Physiology . 45 (6): 1163–79. doi :10.1085/jgp.45.6.1163. PMC 2195242 . PMID 13895926.
- ^ La Camera G, Rauch A, Lüscher HR, Senn W, Fusi S (octubre de 2004). "Modelos mínimos de respuesta neuronal adaptada a corrientes de entrada similares a las in vivo". Neural Computation . 16 (10): 2101–24. doi :10.1162/0899766041732468. PMID 15333209. S2CID 1428381.
- ^ abcdefghijklmn Jolivet R, Rauch A, Lüscher HR, Gerstner W (agosto de 2006). "Predicción del momento de la activación de las neuronas piramidales neocorticales mediante modelos de umbral simples". Journal of Computational Neuroscience . 21 (1): 35–49. doi :10.1007/s10827-006-7074-5. PMID 16633938. S2CID 8911457.
- ^ abcdefghijklmn Pozzorini C, Naud R, Mensi S, Gerstner W (julio de 2013). "Blanqueamiento temporal por adaptación a la ley de potencia en neuronas neocorticales". Nature Neuroscience . 16 (7): 942–8. doi :10.1038/nn.3431. PMID 23749146. S2CID 1873019.
- ^ abcd Gerstner W, van Hemmen JL, Cowan JD (noviembre de 1996). "¿Qué es lo que importa en el bloqueo neuronal?". Neural Computation . 8 (8): 1653–76. doi :10.1162/neco.1996.8.8.1653. PMID 8888612. S2CID 1301248.
- ^ abc Izhikevich EM (noviembre de 2003). "Modelo simple de neuronas en pico". IEEE Transactions on Neural Networks . 14 (6): 1569–72. doi :10.1109/TNN.2003.820440. PMID 18244602. S2CID 814743.
- ^ abcdef Naud R, Marcille N, Clopath C, Gerstner W (noviembre de 2008). "Patrones de disparo en el modelo de integración y disparo exponencial adaptativo". Cibernética biológica . 99 (4–5): 335–47. doi :10.1007/s00422-008-0264-7. PMC 2798047 . PMID 19011922.
- ^ abcdefghijklmnopqr Wulfram Gerstner W, Kistler WM, Naud R, Paninski L (24 de julio de 2014). Dinámica neuronal: de neuronas individuales a redes y modelos de cognición. Cambridge, Reino Unido. ISBN 978-1-107-06083-8.OCLC 861774542 .
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Richardson MJ, Brunel N, Hakim V (mayo de 2003). "De la resonancia subumbral a la resonancia de frecuencia de disparo". Journal of Neurophysiology . 89 (5): 2538–54. doi :10.1152/jn.00955.2002. PMID 12611957.
- ^ ab Lundstrom BN, Higgs MH, Spain WJ, Fairhall AL (noviembre de 2008). "Diferenciación fraccional por neuronas piramidales neocorticales". Nature Neuroscience . 11 (11): 1335–42. doi :10.1038/nn.2212. PMC 2596753 . PMID 18931665.
- ^ ab Teka W, Marinov TM, Santamaria F (marzo de 2014). "Adaptación de la sincronización de picos neuronales descrita con un modelo de integración y disparo con fugas fraccionales". PLOS Computational Biology . 10 (3): e1003526. Bibcode :2014PLSCB..10E3526T. doi : 10.1371/journal.pcbi.1003526 . PMC 3967934 . PMID 24675903.
- ^ abcde Badel L, Lefort S, Brette R, Petersen CC, Gerstner W , Richardson MJ (febrero de 2008). "Las curvas IV dinámicas son predictores fiables de trazas de voltaje de neuronas piramidales naturalistas". Journal of Neurophysiology . 99 (2): 656–66. CiteSeerX 10.1.1.129.504 . doi :10.1152/jn.01107.2007. PMID 18057107.
- ^ ab Brette R, Gerstner W (noviembre de 2005). "Modelo de integración y disparo exponencial adaptativo como descripción eficaz de la actividad neuronal". Journal of Neurophysiology . 94 (5): 3637–42. doi :10.1152/jn.00686.2005. PMID 16014787.
- ^ ab Fourcaud-Trocmé N, Hansel D, van Vreeswijk C, Brunel N (diciembre de 2003). "Cómo los mecanismos de generación de picos determinan la respuesta neuronal a las entradas fluctuantes". The Journal of Neuroscience . 23 (37): 11628–40. doi :10.1523/JNEUROSCI.23-37-11628.2003. PMC 6740955 . PMID 14684865.
- ^ Ostojic S, Brunel N, Hakim V (agosto de 2009). "Cómo la conectividad, la actividad de fondo y las propiedades sinápticas dan forma a la correlación cruzada entre trenes de picos". The Journal of Neuroscience . 29 (33): 10234–53. doi :10.1523/JNEUROSCI.1275-09.2009. PMC 6665800 . PMID 19692598.
- ^ Górski T, Depannemaecker D, Destexhe A (enero de 2021). "Modelo de integración y disparo exponencial adaptativo basado en conductancia". Computación neuronal . 33 (1): 41–66. doi : 10.1162/neco_a_01342 . PMID 33253029.
- ^ "Dinámica neuronal: un libro de texto sobre neurociencia de Wulfram Gerstner, Werner M. Kistler, Richard Naud y Liam Paninski". neuronaldynamics.epfl.ch . Consultado el 14 de febrero de 2024 .
- ^ Ganguly, Chittotosh; Bezugam, Sai Sukruth; Abs, Elisabeth; Payvand, Melika; Dey, Sounak; Suri, Manan (1 de febrero de 2024). "Adaptación de frecuencia de pico: vinculando modelos neuronales y aplicaciones neuromórficas". Ingeniería de comunicaciones . 3 (1): 22. doi : 10.1038/s44172-024-00165-9 . ISSN 2731-3395. PMC 11053160 .
- ^ Bellec, Guillaume Emmanuel Fernand; Salaj, Darjan; Subramoney, Anand; Legenstein, Robert; Maass, Wolfgang (2018). "Memoria a corto plazo y aprendizaje a aprender en redes de neuronas activas". Avances en sistemas de procesamiento de información neuronal . arXiv : 1803.09574 .
- ^ Shaban, Ahmed; Bezugam, Sai Sukruth; Suri, Manan (9 de julio de 2021). "Una neurona de umbral adaptativa para redes neuronales de picos recurrentes con implementación de hardware de nanodispositivos". Nature Communications . 12 (1): 4234. Bibcode :2021NatCo..12.4234S. doi :10.1038/s41467-021-24427-8. ISSN 2041-1723. PMC 8270926 . PMID 34244491.
- ^ Bezugam, Sai Sukruth; Shaban, Ahmed; Suri, Manan (21 de mayo de 2023). "Redes neuronales neuromórficas de picos recurrentes para la clasificación de gestos EMG y la implementación de baja potencia en Loihi". Simposio internacional IEEE sobre circuitos y sistemas (ISCAS) de 2023. IEEE. págs. 1–5. arXiv : 2206.02061 . doi :10.1109/ISCAS46773.2023.10181510. ISBN . 978-1-6654-5109-3. Número de identificación del sujeto 260004324.
- ^ Kobayashi, Ryota; Tsubo, Yasuhiro; Shinomoto, Shigeru (2009). "Modelo de neurona de activación hecho a medida equipado con un umbral adaptativo multi-escala de tiempo". Frontiers in Computational Neuroscience . 3 : 9. doi : 10.3389/neuro.10.009.2009 . ISSN 1662-5188. PMC 2722979 . PMID 19668702.
- ^ Bryant HL, Segundo JP (septiembre de 1976). "Iniciación de picos por corriente transmembrana: un análisis de ruido blanco". The Journal of Physiology . 260 (2): 279–314. doi :10.1113/jphysiol.1976.sp011516. PMC 1309092 . PMID 978519.
- ^ Mainen ZF, Sejnowski TJ (junio de 1995). "Fiabilidad de la sincronización de las espigas en las neuronas neocorticales". Science . 268 (5216): 1503–6. Bibcode :1995Sci...268.1503M. doi :10.1126/science.7770778. PMID 7770778.
- ^ Manwani A, Koch C (noviembre de 1999). "Detección y estimación de señales en estructuras de cables ruidosos, I: fuentes de ruido neuronal". Neural Computation . 11 (8): 1797–829. doi :10.1162/089976699300015972. PMID 10578033. S2CID 12298894. Archivado desde el original el 2021-03-07 . Consultado el 2021-04-04 .
- ^ abcd Stein RB (marzo de 1965). "Un análisis teórico de la variabilidad neuronal". Revista biofísica . 5 (2): 173–94. Bibcode :1965BpJ.....5..173S. doi :10.1016/s0006-3495(65)86709-1. PMC 1367716 . PMID 14268952.
- ^ abcdefghi Gerstner W, van Hemmen JL (enero de 1992). "Memoria asociativa en una red de neuronas 'activas'". Red: Computación en sistemas neuronales . 3 (2): 139–164. doi :10.1088/0954-898X_3_2_004. ISSN 0954-898X.
- ^ ab Ditlevsen S, Lansky P (enero de 2005). "Estimación de los parámetros de entrada en el modelo neuronal de Ornstein-Uhlenbeck". Physical Review E . 71 (1 Pt 1): 011907. Bibcode :2005PhRvE..71a1907D. doi :10.1103/PhysRevE.71.011907. PMID 15697630.
- ^ Richardson MJ (agosto de 2007). "Respuesta de la tasa de activación de neuronas lineales y no lineales de integración y activación a un impulso sináptico modulado basado en corriente y conductancia". Physical Review E . 76 (2 Pt 1): 021919. Bibcode :2007PhRvE..76b1919R. doi :10.1103/PhysRevE.76.021919. PMID 17930077.
- ^ Brunel N (1 de mayo de 2000). "Dinámica de redes escasamente conectadas de neuronas excitadoras e inhibidoras". Journal of Computational Neuroscience . 8 (3): 183–208. doi :10.1023/A:1008925309027. PMID 10809012. S2CID 1849650.
- ^ Johannesma PI (1968). "Modelos de difusión para la actividad estocástica de las neuronas". En Caianelleo ER (ed.). Redes neuronales . Springer. págs. 116–144. ISBN 9783642875960.
- ^ Gerstner W, van Hemmen JL (1992-01-01). "Memoria asociativa en una red de neuronas 'activas'". Red: Computación en sistemas neuronales . 3 (2): 139–164. doi :10.1088/0954-898X_3_2_004. ISSN 0954-898X.
- ^ Gerstner W (enero de 1995). "Estructura temporal de la actividad en modelos de redes neuronales" (PDF) . Physical Review E . 51 (1): 738–758. Bibcode :1995PhRvE..51..738G. doi :10.1103/PhysRevE.51.738. PMID 9962697.
- ^ Truccolo W, Eden UT, Fellows MR, Donoghue JP, Brown EN (febrero de 2005). "Un marco de proceso puntual para relacionar la actividad de picos neuronales con el historial de picos, el conjunto neuronal y los efectos covariables extrínsecos". Journal of Neurophysiology . 93 (2): 1074–89. doi :10.1152/jn.00697.2004. PMID 15356183.
- ^ abcd Pillow JW, Shlens J, Paninski L, Sher A, Litke AM, Chichilnisky EJ, Simoncelli EP (agosto de 2008). "Correlaciones espacio-temporales y señalización visual en una población neuronal completa". Nature . 454 (7207): 995–9. Bibcode :2008Natur.454..995P. doi :10.1038/nature07140. PMC 2684455 . PMID 18650810.
- ^ Weiss TF (noviembre de 1966). "Un modelo del sistema auditivo periférico". Kybernetik . 3 (4): 153–75. doi :10.1007/BF00290252. PMID 5982096. S2CID 30861035.
- ^ abcdefghi Gerstner W (enero de 2000). "Dinámica de población de neuronas activas: transitorios rápidos, estados asincrónicos y bloqueo" (PDF) . Neural Computation . 12 (1): 43–89. doi :10.1162/089976600300015899. PMID 10636933. S2CID 7832768.
- ^ Naud R, Gerstner W (4 de octubre de 2012). Sporns O (ed.). "Codificación y decodificación con neuronas adaptables: un enfoque poblacional para el histograma de tiempo peri-estímulo". PLOS Computational Biology . 8 (10): e1002711. Bibcode :2012PLSCB...8E2711N. doi : 10.1371/journal.pcbi.1002711 . PMC 3464223 . PMID 23055914.
- ^ Gerstner W, Ritz R, van Hemmen JL (octubre de 1993). "¿Por qué picos? Aprendizaje hebbiano y recuperación de patrones de excitación resueltos en el tiempo". Cibernética biológica . 69 (5–6): 503–15. doi :10.1007/BF00199450. PMID 7903867. S2CID 6195748.
- ^ ab Paninski L (noviembre de 2004). "Estimación de máxima verosimilitud de modelos de codificación neuronal de procesos puntuales en cascada". Red: Computación en sistemas neuronales . 15 (4): 243–62. doi : 10.1088/0954-898X_15_4_002 . PMID 15600233. S2CID 848548.
- ^ abcd Kistler WM, Gerstner W, Hemmen JL (1 de julio de 1997). "Reducción de las ecuaciones de Hodgkin-Huxley a un modelo de umbral de una sola variable". Neural Computation . 9 (5): 1015–1045. doi :10.1162/neco.1997.9.5.1015. ISSN 0899-7667. S2CID 9861477.
- ^ ab Gerstner W (enero de 1995). "Estructura temporal de la actividad en modelos de redes neuronales". Physical Review E . 51 (1): 738–758. Bibcode :1995PhRvE..51..738G. doi :10.1103/PhysRevE.51.738. PMID 9962697.
- ^ Galves A, Löcherbach E (2013). "Sistemas infinitos de cadenas interactuantes con memoria de longitud variable: un modelo estocástico para redes neuronales biológicas". Journal of Statistical Physics . 151 (5): 896–921. arXiv : 1212.5505 . Bibcode :2013JSP...151..896G. doi :10.1007/s10955-013-0733-9. S2CID 119161279.
- ^ Fitzhugh R (julio de 1961). "Impulsos y estados fisiológicos en modelos teóricos de la membrana nerviosa". Revista biofísica . 1 (6): 445–66. Bibcode :1961BpJ.....1..445F. doi :10.1016/S0006-3495(61)86902-6. PMC 1366333 . PMID 19431309.
- ^ FitzHugh R, Izhikevich E (2006). "Modelo FitzHugh-Nagumo". Scholarpedia . 1 (9): 1349. Código Bibliográfico :2006SchpJ...1.1349I. doi : 10.4249/scholarpedia.1349 .
- ^ abcd Métodos de modelado neuronal: de iones a redes (02 ed.). [Lugar de publicación no identificado]: Mit Press. 2003. ISBN 0-262-51713-2.OCLC 947133821 .
- ^ Rinzel J, Ermentrout B (agosto de 1998). "Capítulo 7: Análisis de la excitabilidad y oscilaciones neuronales". En Segev I, Koch C (eds.). Métodos de modelado neuronal . MIT Press. pág. 251. ISBN 978-0262517133.
- ^ ab Hindmarsh J, Cornelius P (1 de octubre de 2005). "El desarrollo del modelo de Hindmarsh-Rose para el estallido". Estallido . WORLD SCIENTIFIC. págs. 3–18. doi :10.1142/9789812703231_0001. ISBN . 978-981-256-506-8.
- ^ ab Ermentrout G, Kopell N (1986). "Estallido parabólico en un sistema excitable acoplado a una oscilación lenta". Revista SIAM de Matemáticas Aplicadas . 46 (2): 233–253. doi :10.1137/0146017. ISSN 0036-1399.
- ^ ab Ermentrout B (julio de 1996). "Membranas de tipo I, curvas de restablecimiento de fase y sincronía". Neural Computation . 8 (5): 979–1001. doi :10.1162/neco.1996.8.5.979. PMID 8697231. S2CID 17168880.
- ^ ab Siebert WM (1970-05-01). "Discriminación de frecuencia en el sistema auditivo: ¿mecanismos de lugar o periodicidad?". Actas del IEEE . 58 (5): 723–730. doi :10.1109/PROC.1970.7727. ISSN 0018-9219.
- ^ ab Siebert WM (junio de 1965). "Algunas implicaciones del comportamiento estocástico de las neuronas auditivas primarias". Kybernetik . 2 (5): 206–15. doi :10.1007/BF00306416. PMID 5839007. S2CID 9744183.
- ^ abcdefghij Nossenson N, Messer H (2010). "Modelado del patrón de activación de neuronas mediante una cadena de Markov de dos estados". Taller sobre procesamiento de señales multicanal y matrices de sensores IEEE 2010. doi :10.1109/SAM.2010.5606761. ISBN 978-1-4244-8978-7.S2CID10973225 .
- ^ abcdefg Nossenson N, Messer H (abril de 2012). "Detección secuencial óptima de estímulos a partir de registros multiunitarios tomados en regiones cerebrales densamente pobladas". Neural Computation . 24 (4): 895–938. doi :10.1162/NECO_a_00257. PMID 22168560. S2CID 16994688.
- ^ abcdefghijklmn Nossenson N, Magal N, Messer H (2016). "Detección de estímulos de la actividad multineuronal: estudio empírico e implicaciones teóricas". Neurocomputing . 174 : 822–837. doi :10.1016/j.neucom.2015.10.007.
- ^ Berry MJ, Meister M (marzo de 1998). "Refractariedad y precisión neuronal". The Journal of Neuroscience . 18 (6): 2200–11. doi :10.1523/JNEUROSCI.18-06-02200.1998. PMC 6792934 . PMID 9482804.
- ^ ab Kass RE, Ventura V (agosto de 2001). "Un modelo de probabilidad de tren de picos". Computación neuronal . 13 (8): 1713–20. doi :10.1162/08997660152469314. PMID 11506667. S2CID 9909632.
- ^ ab Gaumond RP, Molnar CE, Kim DO (septiembre de 1982). "Dependencia del estímulo y la recuperación de la probabilidad de descarga de las espigas de las fibras nerviosas cocleares de los gatos". Journal of Neurophysiology . 48 (3): 856–73. doi :10.1152/jn.1982.48.3.856. PMID 6290620.
- ^ Miller MI, Mark KE (julio de 1992). "Un estudio estadístico de los patrones de descarga del nervio coclear en respuesta a estímulos complejos del habla". Revista de la Sociedad Acústica de Estados Unidos . 92 (1): 202–9. Bibcode :1992ASAJ...92..202M. doi :10.1121/1.404284. PMID 1324958.
- ^ ab Johnson DH, Swami A (agosto de 1983). "La transmisión de señales por patrones de descarga de fibras del nervio auditivo". Revista de la Sociedad Acústica de América . 74 (2): 493–501. Bibcode :1983ASAJ...74..493J. doi :10.1121/1.389815. PMID 6311884.
- ^ Chichilnisky EJ (mayo de 2001). "Un análisis simple de ruido blanco de las respuestas neuronales a la luz". Red: Computación en sistemas neuronales . 12 (2): 199–213. doi :10.1080/713663221. PMID 11405422.
- ^ abcde Nossenson N (2013). Model Based Detection of a Stimulus Presence from Neurophysiological Signals (PDF) (tesis doctoral). Biblioteca Neiman de Ciencias Exactas e Ingeniería, Universidad de Tel Aviv: Universidad de Tel-Aviv. Archivado desde el original (PDF) el 5 de marzo de 2017. Consultado el 12 de abril de 2016 .
- ^ Koehler SD, Pradhan S, Manis PB, Shore SE (febrero de 2011). "Las entradas somatosensoriales modifican la sincronización de las puntas auditivas en las células principales del núcleo coclear dorsal". The European Journal of Neuroscience . 33 (3): 409–20. doi :10.1111/j.1460-9568.2010.07547.x. PMC 3059071 . PMID 21198989.
- ^ Reches A, Gutfreund Y (febrero de 2008). "Adaptaciones específicas de estímulos en el sistema de control de la mirada de la lechuza común". The Journal of Neuroscience . 28 (6): 1523–33. doi :10.1523/JNEUROSCI.3785-07.2008. PMC 6671572 . PMID 18256273.
- ^ Wang X, Lu T, Snider RK, Liang L (mayo de 2005). "Descargas sostenidas en la corteza auditiva provocadas por estímulos preferidos". Nature . 435 (7040): 341–6. Bibcode :2005Natur.435..341W. doi :10.1038/nature03565. PMID 15902257. S2CID 4312195.
- ^ Taberner AM, Liberman MC (enero de 2005). "Propiedades de respuesta de fibras nerviosas auditivas individuales en el ratón". Journal of Neurophysiology . 93 (1): 557–69. doi :10.1152/jn.00574.2004. PMID 15456804.
- ^ Hennevin E, Hars B, Maho C, Bloch V (1 de julio de 1995). "Procesamiento de la información aprendida en el sueño paradójico: relevancia para la memoria". Investigación sobre el cerebro conductual . La función del sueño. 69 (1–2): 125–35. doi :10.1016/0166-4328(95)00013-J. PMID 7546303. S2CID 4034082.
- ^ Rodieck RW (diciembre de 1965). "Análisis cuantitativo de la respuesta de las células ganglionares de la retina del gato a los estímulos visuales". Vision Research . 5 (11): 583–601. doi :10.1016/0042-6989(65)90033-7. PMID 5862581.
- ^ ab Enroth-Cugell C, Lennie P (junio de 1975). "El control de la descarga de las células ganglionares de la retina por los alrededores del campo receptivo". The Journal of Physiology . 247 (3): 551–78. doi :10.1113/jphysiol.1975.sp010947. PMC 1309488 . PMID 1142301.
- ^ Enroth-Cugell C, Shapley RM (septiembre de 1973). "Adaptación y dinámica de las células ganglionares de la retina del gato". The Journal of Physiology . 233 (2): 271–309. doi :10.1113/jphysiol.1973.sp010308. PMC 1350567 . PMID 4747229.
- ^ Sagdullaev BT, McCall MA (1 de septiembre de 2005). "El tamaño y la intensidad del estímulo alteran las propiedades fundamentales del campo receptivo de las células ganglionares de la retina del ratón in vivo". Neurociencia visual . 22 (5): 649–59. doi :10.1017/S0952523805225142. PMID 16332276. S2CID 7699161.
- ^ Nagel KI, Wilson RI (febrero de 2011). "Mecanismos biofísicos que subyacen a la dinámica de las neuronas receptoras olfativas". Nature Neuroscience . 14 (2): 208–16. doi :10.1038/nn.2725. PMC 3030680 . PMID 21217763.
- ^ Tommerdahl M, Delemos KA, Whitsel BL, Favorov OV, Metz CB (julio de 1999). "Respuesta de la corteza parietal anterior al aleteo cutáneo frente a la vibración". Journal of Neurophysiology . 82 (1): 16–33. doi :10.1152/jn.1999.82.1.16. PMID 10400931. S2CID 14729461.
- ^ Hadipour Niktarash A, Shahidi GA (1 de marzo de 2004). "Efectos de la actividad del circuito pedunculopontino-globo pálido interno en la transmisión de las actividades oscilatorias del núcleo subtalámico-globo pálido externo-marcapasos a la corteza". Journal of Computational Neuroscience . 16 (2): 113–27. doi :10.1023/B:JCNS.0000014105.87625.5f. PMID 14758061. S2CID 20728260.
- ^ Yamanaka Y, Kitamura N, Shinohara H, Takahashi K, Shibuya I (enero de 2013). "El glutamato provoca la activación de receptores de kainato en neuronas del lóbulo accesorio del pollo". Journal of Comparative Physiology A: Neuroethology, Sensory, Neural & Behavioral Physiology . 199 (1): 35–43. doi :10.1007/s00359-012-0766-6. PMID 23064516. S2CID 15527085.
- ^ Müller M, Robertson D, Yates GK (septiembre de 1991). "Funciones de frecuencia versus nivel de las fibras del nervio auditivo primario: evidencia de un comportamiento de ley cuadrática de todas las categorías de fibras en el conejillo de indias". Hearing Research . 55 (1): 50–6. doi :10.1016/0378-5955(91)90091-M. PMID 1752794. S2CID 40343090.
- ^ Johnson DH, Kiang NY (julio de 1976). "Análisis de descargas registradas simultáneamente de pares de fibras del nervio auditivo". Biophysical Journal . 16 (7): 719–34. Bibcode :1976BpJ....16..719J. doi :10.1016/s0006-3495(76)85724-4. PMC 1334896 . PMID 938715.
- ^ Bullock TH (1 de enero de 1997). "Fisiología comparada de analizadores acústicos y centrales afines". Acta Oto-Laryngologica. Suplemento . 532 (sup532): 13–21. doi :10.3109/00016489709126139. PMID 9442839.
- ^ Holstein SB, Buchwald JS, Schwafel JA (noviembre de 1969). "Cambios progresivos en los patrones de respuesta auditiva a tonos repetidos durante la vigilia normal y la parálisis". Brain Research . 16 (1): 133–48. doi :10.1016/0006-8993(69)90090-0. PMID 5348845.
- ^ Rizzo JF (junio de 2011). "Actualización de la investigación sobre prótesis de retina: el Proyecto de Implantes de Retina de Boston". Revista de Neurooftalmología . 31 (2): 160–8. doi :10.1097/wno.0b013e31821eb79e. PMID 21593628. S2CID 17213342.
- ^ Peterman MC, Mehenti NZ, Bilbao KV, Lee CJ, Leng T, Noolandi J, et al. (noviembre de 2003). "El chip de sinapsis artificial: una interfaz retiniana flexible basada en el crecimiento dirigido de células retinianas y la estimulación con neurotransmisores". Órganos artificiales . 27 (11): 975–85. doi :10.1046/j.1525-1594.2003.07307.x. PMID 14616516.
- ^ Iezzi R, Finlayson P, Xu Y, Katragadda R (6–9 de septiembre de 2009). Interfaces neuronales basadas en neurotransmisores microfluídicos para prótesis de retina . Conferencia internacional anual de 2009 de la IEEE Engineering in Medicine and Biology Society. Minneapolis: IEEE Engineering in Medicine and Biology Society. págs. 4563–5. doi :10.1109/IEMBS.2009.5332694. ISBN 978-1-4244-3296-7. Número de identificación personal 19963838. Número de identificación personal 2751102.
- ^ Yoshida K, Farina D, Akay M, Jensen W (1 de marzo de 2010). "Técnicas intraneurales e intramusculares multicanal para grabación multiunitaria y uso en prótesis activas". Actas del IEEE . 98 (3): 432–449. doi :10.1109/JPROC.2009.2038613. ISSN 0018-9219. S2CID 23631268.
- ^ Bruns TM, Wagenaar JB, Bauman MJ, Gaunt RA, Weber DJ (abril de 2013). "Control en tiempo real de la estimulación eléctrica funcional de las extremidades posteriores mediante retroalimentación de los registros de los ganglios de la raíz dorsal". Journal of Neural Engineering . 10 (2): 026020. Bibcode :2013JNEng..10b6020B. doi :10.1088/1741-2560/10/2/026020. PMC 3640462 . PMID 23503062.
- ^ "BrainGate - Inicio". braingate2.org . 2015-12-04 . Consultado el 2016-04-06 .
- ^ ab Hay E, Hill S, Schürmann F, Markram H, Segev I (julio de 2011). "Modelos de células piramidales de la capa 5b neocortical que capturan una amplia gama de propiedades activas dendríticas y perisomáticas". PLOS Computational Biology . 7 (7): e1002107. Bibcode :2011PLSCB...7E2107H. doi : 10.1371/journal.pcbi.1002107 . PMC 3145650 . PMID 21829333.
- ^ Markram H, Muller E, Ramaswamy S, Reimann MW, Abdellah M, Sanchez CA, et al. (octubre de 2015). "Reconstrucción y simulación de microcircuitos neocorticales". Cell . 163 (2): 456–92. doi : 10.1016/j.cell.2015.09.029 . PMID 26451489. S2CID 14466831.
- ^ Forrest MD (abril de 2015). "Simulación de la acción del alcohol sobre un modelo detallado de neuronas de Purkinje y un modelo sustituto más simple que se ejecuta >400 veces más rápido". BMC Neuroscience . 16 (27): 27. doi : 10.1186/s12868-015-0162-6 . PMC 4417229 . PMID 25928094.
- ^ Sardi S, Vardi R, Sheinin A, Goldental A, Kanter I (diciembre de 2017). "Nuevos tipos de experimentos revelan que una neurona funciona como múltiples unidades de umbral independientes". Scientific Reports . 7 (1): 18036. Bibcode :2017NatSR...718036S. doi :10.1038/s41598-017-18363-1. PMC 5740076 . PMID 29269849.









![{\displaystyle f(I)={\begin{cases}0,&I\leq I_{\mathrm {th} }\\\left[t_{\mathrm {ref} }-R_{\mathrm {m} }C_{\mathrm {m} }\log \left(1-{\tfrac {V_{\mathrm {th} }}{IR_{\mathrm {m} }}}\right)\right]^{-1},&I>I_{\mathrm {th} }\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d2b9ee97278ff7f139dc76afecd9d3336a35a5b)
![{\displaystyle \tau _{\mathrm {m} }{\frac {dV_{\mathrm {m} }(t)}{dt}}=RI(t)-[V_{\mathrm {m} }(t )-E_ {\mathrm {m} }]-R\sum _ {k}w_ {k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f8345759b126e0ae20788d2be0b5f74b89dd598)
![{\displaystyle \tau _{k}{\frac {dw_{k}(t)}{dt}}=-a_{k}[V_{\mathrm {m} }(t)-E_{\mathrm {m } }]-w_{k}+b_{k}\tau _{k}\sum _{f}\delta (tt^{f})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8561a663fc284164af5004d49dda606de65f3153)



![{\displaystyle {\frac {dV}{dt}}-{\frac {R}{\tau _{m}}}I(t)={\frac {1}{\tau _{m}}}[E_{m}-V+\Delta _{T}\exp \left({\frac {V-V_{T}}{\Delta _{T}}}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2681d0764425e62cdbe8563763546145ac871888)




![{\displaystyle \tau _{m}{\frac {dV}{dt}}=RI(t)+\left[E_{m}-V+\Delta _{T}\exp \left({\frac {V-V_{T}}{\Delta _{T}}}\right)\right]-Rw}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc57795f1765df722678bfca445163588b4898aa)
![{\displaystyle \tau {\frac {dw(t)}{dt}}=-a[V_{\mathrm {m} }(t)-E_{\mathrm {m} }]-w+b\tau \ delta (tt^{f})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ad1061c0bd8fa3f0894982dfd5913c5114471f9)





![{\displaystyle v_{th}(t)=v_{th0}+{\frac {\sum \theta (t-t_{f})}{f}}=v_{th0}+{\frac {\sum \theta _{0}\exp \left[-{\frac {(t-t_{f})}{\tau _{\theta }}}\right]}{f}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3092291632a18a195d5cb17f97c121cac909b46b)
![{\displaystyle \theta (t)=\theta _{0}\exp \left[-{\frac {t}{\tau _{\theta }}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dcd1b31f7ffad6905bffe2135e8160cbab229a5)








![{\displaystyle p_{j1}=\exp \left[-{\frac {\delta t}{\tau _{b1}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5417632ba41e7bf5dd3f3698b17d3f4ca39c7d6e)
![{\displaystyle p_{j2}=\exp \left[-{\frac {\delta t}{\tau _{b2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a1f4efbe00768358ce5e4ba3143407cbf3594a5)




![{\displaystyle \tau_{m}{\frac {dV}{dt}}=[E_{m}-V]+RI(t)+R\xi (t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2471c95b51d6f1a179aaeacc81d4680cbc66d53f)
![{\displaystyle dV=[E_{m}-V+RI(t)]{\frac {dt}{\tau _{m}}}+\sigma \,dW}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c77157af02d1ea4ea0e312efa41ed7083ff17525)

![{\displaystyle \Delta V=[E_{m}-V+RI(t)]{\frac {\Delta t}{\tau _{m}}}+\sigma {\sqrt {\tau _{m} }}y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac593d7a28da8c87a36c135c66923293472f26df)






![{\displaystyle f(V-V_{th})={\frac {1}{\tau _{0}}}\exp[\beta (V-V_{th})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0e6a01b14e279fb530c4c37647a0f4dcf60b1b1)




![{\displaystyle P_{F}(t_{n})=F[V(t_{n})-V_{th}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ef050261c3ab3b90026f75a47810dc554c3fbec)

![{\displaystyle F(x)=0,5[1+\tanh(\gamma x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/506d2b8f3cb095fc95e2993bea559a297013a5ed)

![{\displaystyle F(y_{n})\aproximadamente 1-\exp[y_{n}\Delta t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cafeec2276d1633d2d283c3ba07623c0b3f206d5)





![{\displaystyle f(V-\vartheta (t))={\frac {1}{\tau _{0}}}\exp[\beta (V-\vartheta (t))]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b0258498f0e91cf25539b60de5af5a5b24dcfcb)


















![{\displaystyle f(V-\vartheta )={\frac {1}{\tau _{0}}}\exp[\beta (V-V_{th})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bd95a6edcc2e90476af83affbc51d150042d33b)















![{\displaystyle {\frac {d\theta (t)}{dt}}=(I-I_{0})[1+\cos(\theta )]+[1-\cos(\theta )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecbba69c0c299fc9ba2a49a79be5d607200af4c3)
![{\displaystyle \tau _{\mathrm {m}}}{\frac {dV_{\mathrm {m}}(t)}{dt}}=(I-I_{0})R+[V_{\mathrm {m}}(t)-E_{\mathrm {m}}][V_{\mathrm {m}}(t)-V_{\mathrm {T}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8392a8de9357950491d89517ec59294d6ef35e5)
![{\displaystyle [t,t+\Delta _{t}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a5f74c8e9f1b771d10e66322f05d9692676551b)
![{\displaystyle g[s(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79f02d6c931d32be9a417598bb7164a38b18e7c7)

![{\displaystyle P_{\text{pico}}(t\in [t',t'+\Delta _{t}])=\Delta _{t}\cdot g[s(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c518881857d805263d6674a39ae79d3b830a06c)
![{\displaystyle g[s(t)]\propto s^{2}(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/279ad33854b65b37667308913d562014bdb7f30a)


![{\displaystyle R_{\text{fuego}}(t)={\frac {P_{\text{pico}}(t;\Delta _{t})}{\Delta _{t}}}=[y(t)+R_{0}]\cdot P_{0}(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1038693094674ba67b2e424be6eae51db081721e)
![{\displaystyle {\dot {P}}_{0}=-[y(t)+R_{0}+R_{1}]\cdot P_{0}(t)+R_{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/830fe4d93362af37a7b4d97c1902b7db1826f9e1)


![{\displaystyle I_{\mathrm {AMPA} }(t,V)={\bar {g}}_{\mathrm {AMPA} }\cdot [O]\cdot (V(t)-E_{\mathrm { AMPA} })}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a00bcdac49e857cbf0e2440b47d7760a17d7bdc5)
![{\displaystyle I_{\mathrm {NMDA}}(t,V)={\bar {g}}_{\mathrm {NMDA}}\cdot B(V)\cdot [O]\cdot (V(t)-E_{\mathrm {NMDA}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d0bedfd5fbcaada1bfb385795d52950e6429e10)
![{\displaystyle I_{\mathrm {GABA_{A}} }(t,V)={\bar {g}}_{\mathrm {GABA_{A}} }\cdot ([O_{1}]+[O_ {2}])\cdot (V(t)-E_{\mathrm {Cl} })}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0a4898469d8c0f8a2a1b4fd1620c3f69795f85b)
![{\displaystyle I_{\mathrm {GABA_{B}} }(t,V)={\bar {g}}_{\mathrm {GABA_{B}} }\cdot {\tfrac {[G]^{n }}{[G]^{n}+K_{\mathrm {d} }}}\cdot (V(t)-E_{\mathrm {K} })}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09fdce1c61e28bac586e48a928523772a0f4187f)

















