Reducción de dimensionalidad
La reducción de dimensionalidad , o reducción de dimensión , es la transformación de datos de un espacio de alta dimensión a un espacio de baja dimensión de modo que la representación de baja dimensión conserve algunas propiedades significativas de los datos originales, idealmente cercanas a su dimensión intrínseca . Trabajar en espacios de alta dimensión puede ser indeseable por muchas razones; los datos sin procesar suelen ser escasos como consecuencia de la maldición de la dimensionalidad , y el análisis de los datos suele ser computacionalmente intratable . La reducción de dimensionalidad es común en campos que tratan con grandes cantidades de observaciones y/o grandes cantidades de variables, como el procesamiento de señales , el reconocimiento de voz , la neuroinformática y la bioinformática . [1]
Los métodos se dividen comúnmente en enfoques lineales y no lineales. [1] Los enfoques también se pueden dividir en selección de características y extracción de características . [2] La reducción de dimensionalidad se puede utilizar para la reducción de ruido , la visualización de datos , el análisis de clústeres o como un paso intermedio para facilitar otros análisis.
Selección de funciones
El proceso de selección de características tiene como objetivo encontrar un subconjunto adecuado de las variables de entrada ( características o atributos ) para la tarea en cuestión. Las tres estrategias son: la estrategia de filtro (por ejemplo, ganancia de información ), la estrategia de envoltura (por ejemplo, búsqueda guiada por precisión) y la estrategia integrada (las características se agregan o eliminan mientras se construye el modelo en función de los errores de predicción).
El análisis de datos, como la regresión o la clasificación, se puede realizar en el espacio reducido con mayor precisión que en el espacio original. [3]
Proyección de características
La proyección de características (también llamada extracción de características) transforma los datos del espacio de alta dimensión a un espacio de menos dimensiones. La transformación de datos puede ser lineal, como en el análisis de componentes principales (PCA), pero también existen muchas técnicas de reducción de dimensionalidad no lineal . [4] [5] Para datos multidimensionales, la representación tensorial se puede utilizar en la reducción de dimensionalidad a través del aprendizaje de subespacios multilineales . [6]

Análisis de componentes principales (PCA)
La principal técnica lineal para la reducción de dimensionalidad, el análisis de componentes principales, realiza un mapeo lineal de los datos a un espacio de menor dimensión de tal manera que se maximiza la varianza de los datos en la representación de baja dimensión. En la práctica, se construye la matriz de covarianza (y a veces la de correlación ) de los datos y se calculan los vectores propios en esta matriz. Los vectores propios que corresponden a los valores propios más grandes (los componentes principales) ahora se pueden utilizar para reconstruir una gran fracción de la varianza de los datos originales. Además, los primeros vectores propios a menudo se pueden interpretar en términos del comportamiento físico a gran escala del sistema, porque a menudo contribuyen con la gran mayoría de la energía del sistema, especialmente en sistemas de baja dimensión. Aún así, esto debe probarse caso por caso, ya que no todos los sistemas exhiben este comportamiento. El espacio original (con dimensión del número de puntos) se ha reducido (con pérdida de datos, pero con suerte conservando la varianza más importante) al espacio abarcado por unos pocos vectores propios. [ cita requerida ]
Factorización matricial no negativa (NMF)
La NMF descompone una matriz no negativa en el producto de dos no negativas, lo que ha sido una herramienta prometedora en campos donde solo existen señales no negativas, [7] [8] como la astronomía. [9] [10] La NMF es bien conocida desde la regla de actualización multiplicativa de Lee y Seung, [7] que se ha desarrollado continuamente: la inclusión de incertidumbres, [9] la consideración de datos faltantes y computación paralela, [11] construcción secuencial [11] que conduce a la estabilidad y linealidad de la NMF, [10] así como otras actualizaciones que incluyen el manejo de datos faltantes en el procesamiento de imágenes digitales . [12]
Con una base de componentes estable durante la construcción y un proceso de modelado lineal, el NMF secuencial [11] es capaz de preservar el flujo en la obtención de imágenes directas de estructuras circunestelares en astronomía, [10] como uno de los métodos de detección de exoplanetas , especialmente para la obtención de imágenes directas de discos circunestelares . En comparación con el PCA, el NMF no elimina la media de las matrices, lo que conduce a flujos físicos no negativos; por lo tanto, el NMF es capaz de preservar más información que el PCA, como lo demostraron Ren et al. [10].
PCA del núcleo
El análisis de componentes principales se puede emplear de forma no lineal mediante el truco del núcleo . La técnica resultante es capaz de construir mapeos no lineales que maximizan la varianza en los datos. La técnica resultante se denomina PCA del núcleo .
PCA del núcleo basado en gráficos
Otras técnicas no lineales destacadas incluyen técnicas de aprendizaje múltiple como Isomap , incrustación lineal local (LLE), [13] LLE hessiana, mapas propios laplacianos y métodos basados en el análisis del espacio tangente. [14] Estas técnicas construyen una representación de datos de baja dimensión utilizando una función de costo que conserva las propiedades locales de los datos y pueden considerarse como la definición de un núcleo basado en gráficos para Kernel PCA.
Más recientemente, se han propuesto técnicas que, en lugar de definir un núcleo fijo, intentan aprender el núcleo utilizando programación semidefinida . El ejemplo más destacado de una técnica de este tipo es el despliegue de varianza máxima (MVU). La idea central del MVU es preservar exactamente todas las distancias por pares entre los vecinos más cercanos (en el espacio del producto interno) mientras se maximizan las distancias entre los puntos que no son los vecinos más cercanos.
Un enfoque alternativo para la conservación de vecindarios es mediante la minimización de una función de costo que mide las diferencias entre las distancias en los espacios de entrada y salida. Algunos ejemplos importantes de tales técnicas incluyen: escalamiento multidimensional clásico , que es idéntico al PCA; Isomap , que utiliza distancias geodésicas en el espacio de datos; mapas de difusión , que utilizan distancias de difusión en el espacio de datos; incrustación de vecinos estocásticos con distribución t (t-SNE), que minimiza la divergencia entre distribuciones sobre pares de puntos; y análisis de componentes curvilíneos.
Un enfoque diferente para la reducción de la dimensionalidad no lineal es mediante el uso de autocodificadores , un tipo especial de redes neuronales de propagación hacia adelante con una capa oculta de cuello de botella. [15] El entrenamiento de codificadores profundos se realiza típicamente utilizando un preentrenamiento codicioso por capas (por ejemplo, utilizando una pila de máquinas de Boltzmann restringidas ) que es seguido por una etapa de ajuste fino basada en retropropagación .
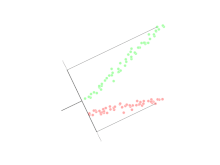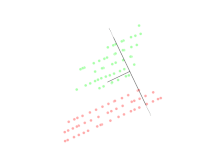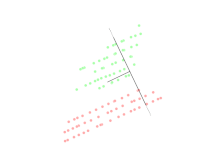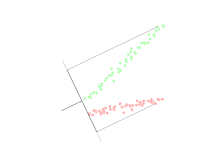
Análisis discriminante lineal (LDA)
El análisis discriminante lineal (LDA) es una generalización del discriminante lineal de Fisher, un método utilizado en estadística, reconocimiento de patrones y aprendizaje automático para encontrar una combinación lineal de características que caracterice o separe dos o más clases de objetos o eventos.
Análisis discriminante generalizado (GDA)
El GDA se ocupa del análisis discriminante no lineal utilizando el operador de función kernel. La teoría subyacente es similar a las máquinas de vectores de soporte (SVM) en la medida en que el método GDA proporciona una proyección de los vectores de entrada en un espacio de características de alta dimensión. [16] [17] De manera similar al LDA, el objetivo del GDA es encontrar una proyección para las características en un espacio de menor dimensión maximizando la relación entre la dispersión entre clases y la dispersión dentro de las clases.
Codificador automático
Los autocodificadores se pueden utilizar para aprender funciones de reducción de dimensión no lineal y codificaciones junto con una función inversa de la codificación a la representación original.
t-SNE
La incrustación estocástica de vecinos distribuida en t (t-SNE) es una técnica de reducción de dimensionalidad no lineal útil para la visualización de conjuntos de datos de alta dimensión. No se recomienda su uso en análisis como la agrupación o la detección de valores atípicos, ya que no necesariamente conserva bien las densidades o las distancias. [18]
Mapa de la Unión
La aproximación y proyección de variedades uniformes (UMAP) es una técnica de reducción de dimensionalidad no lineal. Visualmente, es similar a la t-SNE, pero supone que los datos se distribuyen uniformemente en una variedad de Riemann localmente conectada y que la métrica de Riemann es localmente constante o aproximadamente localmente constante.
Reducción de dimensión
En el caso de conjuntos de datos de alta dimensión, la reducción de dimensión generalmente se realiza antes de aplicar un algoritmo de k vecinos más cercanos ( k -NN) para evitar los efectos de la maldición de la dimensionalidad . [19]
La extracción de características y la reducción de dimensión se pueden combinar en un solo paso, utilizando técnicas de análisis de componentes principales (PCA), análisis discriminante lineal (LDA), análisis de correlación canónica (CCA) o factorización matricial no negativa (NMF) para preprocesar los datos, seguido de la agrupación mediante k -NN en vectores de características en un espacio de dimensión reducida. En el aprendizaje automático , este proceso también se denomina incrustación de baja dimensión . [20]
Para conjuntos de datos de alta dimensión (por ejemplo, cuando se realiza una búsqueda de similitud en transmisiones de video en vivo, datos de ADN o series de tiempo de alta dimensión ), ejecutar una búsqueda rápida aproximada de k -NN utilizando hash sensible a la localidad , proyección aleatoria , [21] "bocetos", [22] u otras técnicas de búsqueda de similitud de alta dimensión de la caja de herramientas de la conferencia VLDB puede ser la única opción factible.
Aplicaciones
Una técnica de reducción de dimensionalidad que a veces se utiliza en neurociencia son las dimensiones máximamente informativas , [ cita requerida ] que encuentran una representación de menor dimensión de un conjunto de datos de modo que se conserve la mayor cantidad de información posible sobre los datos originales.
Véase también
| Sistemas de recomendación |
|---|
| Conceptos |
| Métodos y desafíos |
| Implementations |
| Research |
- Aproximación de la matriz CUR
- Transformación de datos (estadísticas)
- Optimización de hiperparámetros
- Ganancia de información en árboles de decisión
- Lema de Johnson-Lindenstrauss
- Análisis semántico latente
- Alineación del espacio tangente local
- Hashing sensible a la localidad
- MinHash
- Reducción de la dimensionalidad multifactorial
- Búsqueda de vecino más cercano
- Reducción de dimensionalidad no lineal
- Proyección aleatoria
- Mapeo de Sammon
- Mapeo semántico (estadísticas)
- Incrustación semidefinida
- Descomposición en valores singulares
- Reducción suficiente de la dimensión
- Análisis de datos topológicos
- Análisis de redes de correlación ponderada
Notas
- ^ ab van der Maaten, Laurens; Postma, Eric; van den Herik, Jaap (26 de octubre de 2009). "Reducción de dimensionalidad: una revisión comparativa" (PDF) . J Mach Aprender Res . 10 : 66–71.
- ^ Pudil, P.; Novovičová, J. (1998). "Nuevos métodos para la selección de subconjuntos de características con respecto al conocimiento del problema". En Liu, Huan; Motoda, Hiroshi (eds.). Extracción, construcción y selección de características . p. 101. doi :10.1007/978-1-4615-5725-8_7. ISBN 978-1-4613-7622-4.
- ^ Rico-Sulayes, Antonio (2017). "Reducción de la dimensionalidad del espacio vectorial en la clasificación automática para la atribución de autoría". Revista Ingeniería Electrónica, Automática y Comunicaciones . 38 (3): 26–35. ISSN 1815-5928.
- ^ Samet, H. (2006) Fundamentos de estructuras de datos multidimensionales y métricas . Morgan Kaufmann. ISBN 0-12-369446-9
- ^ C. Ding, X. He, H. Zha, HD Simon, Reducción de dimensión adaptativa para agrupamiento de datos de alta dimensión, Actas de la Conferencia internacional sobre minería de datos, 2002
- ^ Lu, Haiping; Plataniotis, KN; Venetsanopoulos, AN (2011). "Un estudio sobre aprendizaje de subespacios multilineales para datos tensoriales" (PDF) . Reconocimiento de patrones . 44 (7): 1540–1551. Código Bibliográfico :2011PatRe..44.1540L. doi :10.1016/j.patcog.2011.01.004.
- ^ ab Daniel D. Lee y H. Sebastian Seung (1999). "Aprendizaje de las partes de los objetos mediante factorización de matrices no negativas". Nature . 401 (6755): 788–791. Bibcode :1999Natur.401..788L. doi :10.1038/44565. PMID 10548103. S2CID 4428232.
- ^ Daniel D. Lee y H. Sebastian Seung (2001). Algoritmos para la factorización de matrices no negativas (PDF) . Avances en sistemas de procesamiento de información neuronal 13: Actas de la conferencia de 2000. MIT Press . págs. 556–562.
- ^ ab Blanton, Michael R.; Roweis, Sam (2007). "Correcciones K y transformaciones de filtros en el ultravioleta, óptico e infrarrojo cercano". The Astronomical Journal . 133 (2): 734–754. arXiv : astro-ph/0606170 . Código Bibliográfico :2007AJ....133..734B. doi :10.1086/510127. S2CID 18561804.
- ^ abcd Ren, Bin; Pueyo, Laurent; Zhu, Guangtun B.; Duchêne, Gaspard (2018). "Factorización de matrices no negativas: extracción robusta de estructuras extendidas". The Astrophysical Journal . 852 (2): 104. arXiv : 1712.10317 . Código Bibliográfico :2018ApJ...852..104R. doi : 10.3847/1538-4357/aaa1f2 . S2CID 3966513.
- ^ abc Zhu, Guangtun B. (19 de diciembre de 2016). "Factorización de matrices no negativas (NMF) con incertidumbres heterocedásticas y datos faltantes". arXiv : 1612.06037 [astro-ph.IM].
- ^ Ren, Bin; Pueyo, Laurent; Chen, Christine; Choquet, Elodie; Debes, John H.; Duechene, Gaspard; Menard, Francois; Perrin, Marshall D. (2020). "Uso de imputación de datos para la separación de señales en imágenes de alto contraste". The Astrophysical Journal . 892 (2): 74. arXiv : 2001.00563 . Código Bibliográfico :2020ApJ...892...74R. doi : 10.3847/1538-4357/ab7024 . S2CID 209531731.
- ^ Roweis, ST; Saul, LK (2000). "Reducción de dimensionalidad no lineal mediante incrustación lineal local". Science . 290 (5500): 2323–2326. Bibcode :2000Sci...290.2323R. CiteSeerX 10.1.1.111.3313 . doi :10.1126/science.290.5500.2323. PMID 11125150. S2CID 5987139.
- ^ Zhang, Zhenyue; Zha, Hongyuan (2004). "Variedades principales y reducción de dimensionalidad no lineal mediante alineación del espacio tangente". Revista SIAM de informática científica . 26 (1): 313–338. Bibcode :2004SJSC...26..313Z. doi :10.1137/s1064827502419154.
- ^ Hongbing Hu, Stephen A. Zahorian, (2010) "Métodos de reducción de dimensionalidad para el reconocimiento fonético HMM", ICASSP 2010, Dallas, TX
- ^ Baudat, G.; Anouar, F. (2000). "Análisis discriminante generalizado utilizando un enfoque de núcleo". Computación neuronal . 12 (10): 2385–2404. CiteSeerX 10.1.1.412.760 . doi :10.1162/089976600300014980. PMID 11032039. S2CID 7036341.
- ^ Haghighat, Mohammad; Zonouz, Saman; Abdel-Mottaleb, Mohamed (2015). "CloudID: Identificación biométrica confiable basada en la nube y entre empresas". Sistemas expertos con aplicaciones . 42 (21): 7905–7916. doi :10.1016/j.eswa.2015.06.025.
- ^ Schubert, Erich; Gertz, Michael (2017). "Incorporación de vecinos t-estocásticos intrínsecos para visualización y detección de valores atípicos". En Beecks, Christian; Borutta, Felix; Kröger, Peer; Seidl, Thomas (eds.). Búsqueda de similitud y aplicaciones . Apuntes de clase en informática. Vol. 10609. Cham: Springer International Publishing. págs. 188–203. doi :10.1007/978-3-319-68474-1_13. ISBN 978-3-319-68474-1.
- ^ Kevin Beyer, Jonathan Goldstein, Raghu Ramakrishnan, Uri Shaft (1999) "¿Cuándo tiene sentido el término "vecino más próximo"?". Teoría de bases de datos—ICDT99 , 217–235
- ^ Shaw, B.; Jebara, T. (2009). "Incrustación que preserva la estructura" (PDF) . Actas de la 26.ª Conferencia internacional anual sobre aprendizaje automático – ICML '09 . pág. 1. CiteSeerX 10.1.1.161.451 . doi :10.1145/1553374.1553494. ISBN. 9781605585161.S2CID8522279 .
- ^ Bingham, E.; Mannila, H. (2001). "Proyección aleatoria en la reducción de dimensionalidad". Actas de la séptima conferencia internacional ACM SIGKDD sobre descubrimiento de conocimiento y minería de datos – KDD '01 . pág. 245. doi :10.1145/502512.502546. ISBN 978-1581133912. Número de identificación del sujeto 1854295.
- ^ Shasha, D High (2004) Descubrimiento del rendimiento en series temporales Berlín: Springer. ISBN 0-387-00857-8
Referencias
- Boehmke, Brad; Greenwell, Brandon M. (2019). "Reducción de dimensión". Aprendizaje automático práctico con R. Chapman & Hall. págs. 343–396. ISBN 978-1-138-49568-5.
- Cunningham, P. (2007). Reducción de dimensiones (informe técnico). University College Dublin. UCD-CSI-2007-7.
- Fodor, I. (2002). Un estudio de las técnicas de reducción de dimensión (informe técnico). Centro de Computación Científica Aplicada, Lawrence Livermore National. UCRL-ID-148494.
- Lakshmi Padmaja, Dhyaram; Vishnuvardhan, B (2016). "Estudio comparativo de métodos de selección de subconjuntos de características para la reducción de la dimensionalidad en datos científicos". 2016 IEEE 6th International Conference on Advanced Computing (IACC) . págs. 31–34. doi :10.1109/IACC.2016.16. ISBN 978-1-4673-8286-1.S2CID 14532363 .
Enlaces externos
- Número especial de JMLR sobre selección de variables y características
- Mapas elásticos Archivado el 20 de julio de 2011 en Wayback Machine
- Incrustación lineal local
- Comparación visual de varios métodos de reducción de dimensionalidad
- Un marco geométrico global para la reducción de la dimensionalidad no lineal