Reflector parabólico

Un reflector parabólico (o paraboloide o paraboloidal ) (o plato o espejo ) es una superficie reflectante que se utiliza para recoger o proyectar energía como luz , sonido o ondas de radio . Su forma es parte de un paraboloide circular , es decir, la superficie generada por una parábola que gira alrededor de su eje. El reflector parabólico transforma una onda plana entrante que viaja a lo largo del eje en una onda esférica que converge hacia el foco. Por el contrario, una onda esférica generada por una fuente puntual colocada en el foco se refleja en una onda plana que se propaga como un haz colimado a lo largo del eje.

Los reflectores parabólicos se utilizan para recoger energía de una fuente distante (por ejemplo, ondas sonoras o luz estelar entrante). Dado que los principios de reflexión son reversibles, los reflectores parabólicos también se pueden utilizar para colimar la radiación de una fuente isótropa en un haz paralelo . ^[1] En óptica , los espejos parabólicos se utilizan para recoger luz en telescopios reflectores y hornos solares , y proyectar un haz de luz en linternas , reflectores , focos de escenario y faros de automóviles . En radio , las antenas parabólicas se utilizan para radiar un haz estrecho de ondas de radio para comunicaciones punto a punto en antenas parabólicas y estaciones de retransmisión de microondas , y para localizar aviones, barcos y vehículos en equipos de radar . En acústica , los micrófonos parabólicos se utilizan para grabar sonidos lejanos como cantos de pájaros , en reportajes deportivos y para espiar conversaciones privadas en espionaje y aplicación de la ley.

Esta sección no cita ninguna fuente . Por favor, ayude a mejorar esta sección añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado . ( Noviembre de 2012 ) ( Aprenda cómo y cuándo eliminar este mensaje )

En sentido estricto, la forma tridimensional del reflector se denomina paraboloide . Una parábola es la figura bidimensional. (La distinción es similar a la que existe entre una esfera y un círculo). Sin embargo, en el lenguaje informal, la palabra parábola y su adjetivo asociado, parabólico, se utilizan a menudo en lugar de paraboloide y paraboloidal . ^[2]

Si una parábola se posiciona en coordenadas cartesianas con su vértice en el origen y su eje de simetría a lo largo del eje y, de modo que la parábola se abre hacia arriba, su ecuación es , donde es su longitud focal. (Ver " Parábola#En un sistema de coordenadas cartesianas ".) Correspondientemente, las dimensiones de un plato paraboloide simétrico están relacionadas por la ecuación: , donde es la longitud focal, es la profundidad del plato (medida a lo largo del eje de simetría desde el vértice hasta el plano del borde), y es el radio del plato desde el centro. Todas las unidades utilizadas para el radio, el punto focal y la profundidad deben ser las mismas. Si se conocen dos de estas tres cantidades, esta ecuación se puede utilizar para calcular la tercera.${\textstyle 4fy=x^{2}}$${\textstyle f}$${\textstyle 4FD=R^{2}}$${\textstyle F}$${\textstyle D}$${\textstyle R}$

Se necesita un cálculo más complejo para encontrar el diámetro del plato medido a lo largo de su superficie . Esto a veces se llama "diámetro lineal", y es igual al diámetro de una lámina plana y circular de material, generalmente metal, que tiene el tamaño adecuado para ser cortada y doblada para hacer el plato. Dos resultados intermedios son útiles en el cálculo: (o el equivalente: ) y , donde F , D y R se definen como se indicó anteriormente. El diámetro del plato, medido a lo largo de la superficie, se da entonces por: , donde significa el logaritmo natural de x , es decir, su logaritmo en base " e ".${\textstyle P=2F}$${\textstyle P={\frac {R^{2}}{2D}}}$${\estilo de texto Q={\sqrt {P^{2}+R^{2}}}}$${\textstyle {\frac {RQ}{P}}+P\ln \left({\frac {R+Q}{P}}\right)}$${\textstyle \ln(x)}$

El volumen del plato se da por donde los símbolos se definen como se indicó anteriormente. Esto se puede comparar con las fórmulas para los volúmenes de un cilindro un hemisferio donde y un cono es el área de apertura del plato, el área encerrada por el borde, que es proporcional a la cantidad de luz solar que el plato reflector puede interceptar. El área de la superficie cóncava del plato se puede encontrar utilizando la fórmula del área para una superficie de revolución que da . proporcionando . La fracción de luz reflejada por el plato, desde una fuente de luz en el foco, se da por , donde y se definen como se indicó anteriormente.${\textstyle {\frac {1}{2}}\pi R^{2}D,}$ ${\textstyle (\pi R^{2}D),}$ ${\textstyle ({\frac {2}{3}}\pi R^{2}D,}$${\textstyle D=R),}$ ${\textstyle ({\frac {1}{3}}\pi R^{2}D).}$ ${\textstyle \pi R^{2}}$${\textstyle A={\frac {\pi R}{6D^{2}}}\left((R^{2}+4D^{2})^{3/2}-R^{3}\right)}$${\textstyle D\neq 0}$${\textstyle 1-{\frac {\arctan {\frac {R}{DF}}}{\pi }}}$${\estilo de visualización F,}$ ${\estilo de visualización D,}$${\estilo de visualización R}$

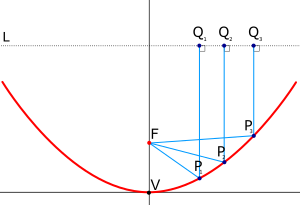
El reflector parabólico funciona gracias a las propiedades geométricas de la forma paraboloide: cualquier rayo incidente que sea paralelo al eje de la antena se reflejará en un punto central o " foco ". (Para una prueba geométrica, haga clic aquí .) Debido a que muchos tipos de energía se pueden reflejar de esta manera, los reflectores parabólicos se pueden utilizar para recolectar y concentrar la energía que ingresa al reflector en un ángulo particular. De manera similar, la energía que irradia desde el foco hacia la antena se puede transmitir hacia afuera en un haz que es paralelo al eje de la antena.

A diferencia de los reflectores esféricos , que sufren una aberración esférica que se hace más fuerte a medida que aumenta la relación entre el diámetro del haz y la distancia focal, los reflectores parabólicos pueden fabricarse para alojar haces de cualquier ancho. Sin embargo, si el haz entrante forma un ángulo distinto de cero con el eje (o si la fuente puntual emisora ​​no está colocada en el foco), los reflectores parabólicos sufren una aberración llamada coma . Esto es de interés principalmente en los telescopios porque la mayoría de las demás aplicaciones no requieren una resolución nítida fuera del eje de la parábola.

La precisión con la que debe fabricarse un plato parabólico para enfocar bien la energía depende de la longitud de onda de la energía. Si el plato está equivocado en un cuarto de longitud de onda, entonces la energía reflejada estará equivocada en media longitud de onda, lo que significa que interferirá destructivamente con la energía que se ha reflejado correctamente desde otra parte del plato. Para evitar esto, el plato debe fabricarse correctamente con una precisión de aproximadamente ⁠1/20⁠ de una longitud de onda. El rango de longitud de onda de la luz visible está entre aproximadamente 400 y 700 nanómetros (nm), por lo que para enfocar bien toda la luz visible, un reflector debe tener una precisión de aproximadamente 20 nm. A modo de comparación, el diámetro de un cabello humano suele ser de unos 50.000 nm, por lo que la precisión requerida para que un reflector enfoque la luz visible es unas 2500 veces menor que el diámetro de un cabello. Por ejemplo, el defecto en el espejo del telescopio espacial Hubble (demasiado plano en unos 2200 nm en su perímetro) provocó una aberración esférica grave hasta que se corrigió con COSTAR . ^[3]

Las microondas, como las que se utilizan para las señales de televisión por satélite, tienen longitudes de onda del orden de diez milímetros, por lo que las antenas parabólicas utilizadas para enfocar estas ondas pueden tener un error de medio milímetro aproximadamente y aun así funcionar bien.

A veces resulta útil que el centro de masa de un plato reflector coincida con su foco . Esto permite girarlo fácilmente para que pueda apuntar a una fuente de luz en movimiento, como el Sol en el cielo, mientras que su foco, donde se encuentra el objetivo, está estacionario. El plato gira alrededor de ejes que pasan por el foco y alrededor de los cuales se equilibra. Si el plato es simétrico y está hecho de material uniforme de espesor constante, y si F representa la longitud focal del paraboloide, esta condición de "enfoque equilibrado" ocurre si la profundidad del plato, medida a lo largo del eje del paraboloide desde el vértice hasta el plano del borde del plato, es 1,8478 veces F . El radio del borde es 2,7187  F . ^[a] El radio angular del borde visto desde el punto focal es 72,68 grados.

La configuración de foco equilibrado (ver arriba) requiere que la profundidad del plato reflector sea mayor que su longitud focal, por lo que el foco está dentro del plato. Esto puede hacer que el foco sea difícil de acceder. Un enfoque alternativo se ejemplifica con el reflector Scheffler , llamado así por su inventor, Wolfgang Scheffler . Este es un espejo paraboloide que gira alrededor de ejes que pasan por su centro de masa, pero esto no coincide con el foco, que está fuera del plato. Si el reflector fuera un paraboloide rígido, el foco se movería cuando el plato gira. Para evitar esto, el reflector es flexible y se dobla a medida que gira para mantener el foco estacionario. Idealmente, el reflector sería exactamente paraboloide en todo momento. En la práctica, esto no se puede lograr con exactitud, por lo que el reflector Scheffler no es adecuado para fines que requieren alta precisión. Se utiliza en aplicaciones como la cocina solar , donde la luz solar debe enfocarse lo suficientemente bien como para incidir en una olla de cocina, pero no en un punto exacto. ^[4]

Un paraboloide circular es teóricamente de tamaño ilimitado. Cualquier reflector práctico utiliza sólo un segmento del mismo. A menudo, el segmento incluye el vértice del paraboloide, donde su curvatura es mayor, y donde el eje de simetría intersecta al paraboloide. Sin embargo, si el reflector se utiliza para enfocar la energía entrante sobre un receptor, la sombra del receptor cae sobre el vértice del paraboloide, que es parte del reflector, por lo que se desperdicia parte del reflector. Esto se puede evitar haciendo el reflector a partir de un segmento del paraboloide que esté desplazado respecto del vértice y el eje de simetría. Todo el reflector recibe energía, que luego se enfoca sobre el receptor. Esto se hace con frecuencia, por ejemplo, en antenas receptoras de televisión por satélite, y también en algunos tipos de telescopios astronómicos ( por ejemplo , el telescopio Green Bank , el telescopio espacial James Webb ).

Los reflectores descentrados precisos para su uso en hornos solares y otras aplicaciones no críticas se pueden fabricar de forma muy sencilla utilizando un horno rotatorio , en el que el recipiente de vidrio fundido está desplazado respecto del eje de rotación. Para fabricar otros menos precisos, adecuados como antenas parabólicas, se diseña la forma mediante un ordenador y luego se estampan varias antenas en chapa metálica.

Los reflectores fuera del eje que se dirigen desde latitudes medias a un satélite de televisión geoestacionario situado en algún lugar por encima del ecuador tienen una inclinación mayor que un reflector coaxial. El efecto es que el brazo que sostiene la antena puede ser más corto y la nieve tiende a acumularse menos en (la parte inferior de) la antena.

El principio de los reflectores parabólicos se conoce desde la antigüedad clásica , cuando el matemático Diocles los describió en su libro Sobre los espejos ardientes y demostró que enfocan un haz paralelo a un punto. ^[5] Arquímedes en el siglo III a. C. estudió los paraboloides como parte de su estudio del equilibrio hidrostático , ^[6] y se ha afirmado que utilizó reflectores para incendiar la flota romana durante el asedio de Siracusa . ^[7] Sin embargo, esto parece poco probable que sea cierto, ya que la afirmación no aparece en fuentes anteriores al siglo II d. C., y Diocles no la menciona en su libro. ^[8] Los espejos parabólicos y los reflectores también fueron estudiados extensamente por el físico Roger Bacon en el siglo XIII d. C. ^[9] James Gregory , en su libro de 1663 Optica Promota (1663), señaló que un telescopio reflector con un espejo parabólico corregiría la aberración esférica, así como la aberración cromática observada en los telescopios refractores . El diseño que ideó lleva su nombre: el " telescopio gregoriano "; pero según su propia confesión, Gregory no tenía habilidades prácticas y no pudo encontrar ningún óptico capaz de construir uno. ^[10] Isaac Newton conocía las propiedades de los espejos parabólicos, pero eligió una forma esférica para el espejo de su telescopio newtoniano para simplificar la construcción. ^[11] Los faros también usaban comúnmente espejos parabólicos para colimar un punto de luz de una linterna en un haz, antes de ser reemplazados por lentes Fresnel más eficientes en el siglo XIX. En 1888, Heinrich Hertz , un físico alemán, construyó la primera antena reflectora parabólica del mundo. ^[12]

Las aplicaciones modernas más comunes del reflector parabólico son en antenas parabólicas , telescopios reflectores , radiotelescopios , micrófonos parabólicos , cocinas solares y muchos dispositivos de iluminación como focos , faros de automóviles , lámparas PAR y carcasas de LED. ^[14]

La llama olímpica se enciende tradicionalmente en Olimpia (Grecia ) mediante un reflector parabólico que concentra la luz solar y luego se transporta hasta la sede de los Juegos. Los espejos parabólicos son una de las muchas formas que tiene el vidrio para encenderse .

Los reflectores parabólicos son populares para crear ilusiones ópticas . Consisten en dos espejos parabólicos opuestos, con una abertura en el centro del espejo superior. Cuando se coloca un objeto en el espejo inferior, los espejos crean una imagen real , que es una copia prácticamente idéntica del original que aparece en la abertura. La calidad de la imagen depende de la precisión de la óptica. Algunas de estas ilusiones se fabrican con tolerancias de millonésimas de pulgada.

Se puede formar un reflector parabólico que apunte hacia arriba haciendo girar un líquido reflectante, como el mercurio, alrededor de un eje vertical. Esto hace posible el telescopio de espejo líquido . La misma técnica se utiliza en hornos rotatorios para fabricar reflectores sólidos.

Los reflectores parabólicos también son una alternativa popular para aumentar la potencia de la señal inalámbrica. Incluso con los más sencillos, los usuarios han informado de ganancias de 3 dB o más. ^{[15] [16]}

• Juan D. Kraus
• Telescopio de espejo líquido , paraboloides producidos por rotación
• Antena parabólica
• Cilindro parabólico
• Horno solar
• Reflector toroidal

• Demostración en Java de un reflector parabólico
• Antenas reflectoras parabólicas www.antenna-theory.com
• Animaciones que demuestran el espejo parabólico mediante QED
• Construir reflectores paraboloides grandes usando segmentos planos