Asistente de pruebas

Herramienta de software para ayudar en el desarrollo de pruebas formales mediante la colaboración hombre-máquina

Una sesión de prueba interactiva en CoqIDE, que muestra el script de prueba a la izquierda y el estado de la prueba a la derecha

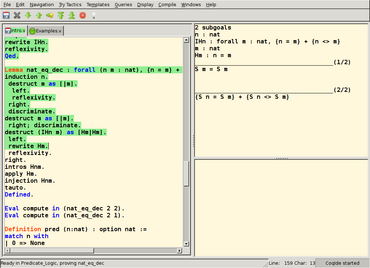
En informática y lógica matemática , un asistente de pruebas o demostrador interactivo de teoremas es una herramienta de software que ayuda a desarrollar pruebas formales mediante la colaboración entre humanos y máquinas. Esto implica algún tipo de editor de pruebas interactivo u otra interfaz con la que un humano puede guiar la búsqueda de pruebas, cuyos detalles se almacenan en una computadora y algunos pasos son proporcionados por ella .

Un esfuerzo reciente dentro de este campo es hacer que estas herramientas utilicen inteligencia artificial para automatizar la formalización de las matemáticas ordinarias. ^[1]

Comparación de sistemas

Nombre	Última versión	Desarrollador(es)	Lenguaje de implementación	Características
Nombre	Última versión	Desarrollador(es)	Lenguaje de implementación	Lógica de orden superior	Tipos dependientes	Grano pequeño	Automatización de pruebas	Prueba por reflexión	Generación de código
ACL2	8.3	Matt Kaufmann y J Strother Moore	Ceceo común	No	Sin tipo	No	Sí	Sí ^[2]	Ya ejecutable
Agadé	2.6.4.3 ^[3]	Ulf Norell, Nils Anders Danielsson y Andreas Abel ( Chalmers y Gotemburgo ) ^[3]	Haskell ^[3]	Sí ^{[ cita requerida ]}	Sí ^[4]	Sí ^{[ cita requerida ]}	No ^{[ cita requerida ]}	Parcial ^{[ cita requerida ]}	Ya ejecutable ^{[ cita requerida ]}
Albatros	0,4	Helmut Brandl	OCaml	Sí	No	Sí	Sí	Desconocido	Aún no implementado
Gallo	8.20.0	INRIA	OCaml	Sí	Sí	Sí	Sí	Sí	Sí
F*	repositorio	Microsoft Research y el INRIA	F*	Sí	Sí	No	Sí	Sí ^[5]	Sí
Luz HOL	repositorio	John Harrison	OCaml	Sí	No	Sí	Sí	No	No
HOL4	Kananaskis-13 (o repositorio)	Michael Norrish, Konrad Slind y otros	ML estándar	Sí	No	Sí	Sí	No	Sí
Idris	2 0.6.0.	Edwin Brady	Idris	Sí	Sí	Sí	Desconocido	Parcial	Sí
Isabelle	Isabelle2024 (mayo de 2024)	Larry Paulson ( Cambridge ), Tobias Nipkow ( Múnich ) y Makarius Wenzel	Aprendizaje automático estándar , Scala	Sí	No	Sí	Sí	Sí	Sí
Inclinarse	v4.7.0 ^[6]	Leonardo de Moura ( Microsoft Research )	C++ , Lean	Sí	Sí	Sí	Sí	Sí	Sí
LEGO	1.3.1	Randy Pollack ( Edimburgo )	ML estándar	Sí	Sí	Sí	No	No	No
Metamatemáticas	versión 0.198 ^[7]	Normando Megill	Norma ANSI C
Mizar	8.1.11	Universidad de Bialystok	Pascal libre	Parcial	Sí	No	No	No	No
Nqthm
NuPRL	5	Universidad de Cornell	Ceceo común	Sí	Sí	Sí	Sí	Desconocido	Sí
PVS	6.0	SRI Internacional	Ceceo común	Sí	Sí	No	Sí	No	Desconocido
Doce	1.7.1	Frank Pfenning y Carsten Schürmann	ML estándar	Sí	Sí	Desconocido	No	No	Desconocido

ACL2 : un lenguaje de programación, una teoría lógica de primer orden y un demostrador de teoremas (con modos interactivos y automáticos) en la tradición de Boyer-Moore.
Coq – Permite la expresión de afirmaciones matemáticas, verifica mecánicamente las pruebas de estas afirmaciones, ayuda a encontrar pruebas formales y extrae un programa certificado de la prueba constructiva de su especificación formal.
Demostradores de teoremas HOL : una familia de herramientas derivadas en última instancia del demostrador de teoremas LCF . En estos sistemas, el núcleo lógico es una biblioteca de su lenguaje de programación. Los teoremas representan elementos nuevos del lenguaje y solo se pueden introducir mediante "estrategias" que garantizan la corrección lógica. La composición de estrategias brinda a los usuarios la capacidad de producir demostraciones significativas con relativamente pocas interacciones con el sistema. Los miembros de la familia incluyen:
- HOL4 : el "descendiente primario", aún en desarrollo activo. Admite tanto Moscow ML como Poly/ML . Tiene una licencia de estilo BSD .
- HOL Light : una "bifurcación minimalista" en auge, basada en OCaml .
- ProofPower: pasó a ser propietario y luego volvió a ser de código abierto. Basado en Standard ML .
IMPS, un sistema interactivo de pruebas matemáticas. ^[8]
Isabelle es un demostrador de teoremas interactivo, sucesor de HOL. El código base principal tiene licencia BSD, pero la distribución Isabelle incluye muchas herramientas complementarias con diferentes licencias.
Jape – Basado en Java.
Inclinarse
LEGO
Matita – Un sistema ligero basado en el Cálculo de Construcciones Inductivas.
MINLOG – Un asistente de prueba basado en lógica mínima de primer orden.
Mizar – Un asistente de pruebas basado en lógica de primer orden, en un estilo de deducción natural , y en la teoría de conjuntos de Tarski-Grothendieck .
PhoX – Un asistente de pruebas basado en lógica de orden superior y extensible.
Sistema de verificación de prototipos (PVS): un lenguaje y sistema de prueba basado en lógica de orden superior.
TPS y ETPS – Demostradores de teoremas interactivos también basados en cálculo lambda de tipos simples, pero basados en una formulación independiente de la teoría lógica y una implementación independiente.

Interfaces de usuario

Una interfaz popular para los asistentes de prueba es Proof General, basado en Emacs , desarrollado en la Universidad de Edimburgo .

Coq incluye CoqIDE, que se basa en OCaml/ Gtk . Isabelle incluye Isabelle/jEdit, que se basa en jEdit y la infraestructura Isabelle/ Scala para el procesamiento de pruebas orientado a documentos. Más recientemente, se han desarrollado extensiones de Visual Studio Code para Coq, ^[9] Isabelle por Makarius Wenzel, ^[10] y para Lean 4 por los desarrolladores de leanprover. ^[11]

Alcance de la formalización

Freek Wiedijk ha estado llevando un ranking de asistentes de demostración según la cantidad de teoremas formalizados de una lista de 100 teoremas conocidos. A septiembre de 2023, solo cinco sistemas han formalizado demostraciones de más del 70% de los teoremas, a saber, Isabelle, HOL Light, Coq, Lean y Metamath. ^[12]^[13]

Pruebas formalizadas notables

La siguiente es una lista de pruebas notables que se han formalizado dentro de los asistentes de prueba.

Teorema	Asistente de pruebas	Año
Teorema de los cuatro colores ^[14]	Gallo	2005
Teorema de Feit-Thompson ^[15]	Gallo	2012
Grupo fundamental del círculo ^[16]	Gallo	2013
Problema de Erdős-Graham ^[17]^[18]	Inclinarse	2022
Conjetura polinómica de Freiman-Ruzsa sobre ^[19] $\mathbb {F}_{2}$	Inclinarse	2023
BB(5) = 47.176.870 ^[20]	Gallo	2024

Véase también

Demostración automática de teoremas : subcampo del razonamiento automático y la lógica matemática
Prueba asistida por computadora : prueba matemática generada al menos parcialmente por computadora.
Verificación formal : comprobar o refutar la exactitud de ciertos algoritmos previstos
Manifiesto QED – Propuesta para una base de datos informática de todo el conocimiento matemático
Teorías de satisfacibilidad módulo – Problema lógico estudiado en informática
Prover9 – es un demostrador de teoremas automatizado para lógica ecuacional y de primer orden

Notas

^ Ornes, Stephen (27 de agosto de 2020). "Quanta Magazine – ¿Qué tan cerca están las computadoras de automatizar el razonamiento matemático?".
^ Hunt, Warren; Matt Kaufmann; Robert Bellarmine Krug; J Moore; Eric W. Smith (2005). "Meta Reasoning in ACL2" (PDF) . Demostración de teoremas en lógica de orden superior . Apuntes de clase en informática. Vol. 3603. págs. 163–178. doi :10.1007/11541868_11. ISBN 978-3-540-28372-0.
^ abc "agda/agda: Agda es un lenguaje de programación de tipado dependiente / demostrador interactivo de teoremas". GitHub . Consultado el 31 de julio de 2024 .
^ "La Wiki de Agda" . Consultado el 31 de julio de 2024 .
^ Buscar "pruebas por reflexión": arXiv :1803.06547
^ "Página de lanzamientos de Lean 4". GitHub . Consultado el 15 de octubre de 2023 .
^ "Versión v0.198 · metamath/Metamath-exe". GitHub .
^ Farmer, William M.; Guttman, Joshua D.; Thayer, F. Javier (1993). "IMPS: Un sistema interactivo de prueba matemática". Journal of Automated Reasoning . 11 (2): 213–248. doi :10.1007/BF00881906. S2CID 3084322 . Consultado el 22 de enero de 2020 .
^ "coq-community/vscoq". 29 de julio de 2024 – vía GitHub.
^ Wenzel, Makarius. "Isabelle" . Consultado el 2 de noviembre de 2019 .
^ "VS Code Lean 4". GitHub . Consultado el 15 de octubre de 2023 .
^ Wiedijk, Freek (15 de septiembre de 2023). "Formalizando 100 teoremas".
^ Geuvers, Herman (febrero de 2009). "Asistentes de prueba: Historia, ideas y futuro". Sādhanā . 34 (1): 3–25. doi : 10.1007/s12046-009-0001-5 . hdl : 2066/75958 . S2CID 14827467.
^ Gonthier, Georges (2008), "Demostración formal: el teorema de los cuatro colores" (PDF) , Notices of the American Mathematical Society , 55 (11): 1382–1393, MR 2463991, archivado (PDF) desde el original el 2011-08-05
^ "Feit Thomson demostró en Coq - Microsoft Research Inria Joint Centre". 19 de noviembre de 2016. Archivado desde el original el 19 de noviembre de 2016. Consultado el 7 de diciembre de 2023 .
^ Licata, Daniel R.; Shulman, Michael (2013). "Cálculo del grupo fundamental del círculo en la teoría de tipos de homotopía". 28.° Simposio anual ACM/IEEE sobre lógica en informática de 2013. págs. 223–232. arXiv : 1301.3443 . doi :10.1109/lics.2013.28. ISBN 978-1-4799-0413-6. S2CID 5661377 . Consultado el 7 de diciembre de 2023 .
^ "Un problema matemático que se ha estado desarrollando durante 3500 años finalmente obtiene una solución". IFLScience . 2022-03-11 . Consultado el 2024-02-09 .
^ Avigad, Jeremy (2023). "Matemáticas y el giro formal". arXiv : 2311.00007 [math.HO].
^ Sloman, Leila (6 de diciembre de 2023). "El 'Equipo A' de matemáticas demuestra un vínculo crítico entre la suma y los conjuntos". Revista Quanta . Consultado el 7 de diciembre de 2023 .
^ "Hemos demostrado que "BB(5) = 47.176.870"". El desafío del castor atareado . 2024-07-02 . Consultado el 2024-07-09 .

Referencias

Barendregt, Henk ; Geuvers, Herman (2001). "18. Asistentes de prueba que utilizan sistemas de tipos dependientes" (PDF) . En Robinson, Alan JA; Voronkov, Andrei (eds.). Manual de razonamiento automatizado . Vol. 2. Elsevier. págs. 1149–. ISBN 978-0-444-50812-6. Archivado desde el original (PDF) el 27 de julio de 2007.
Pfenning, Frank . "17. Marcos lógicos" (PDF) . Manual vol 2 2001 . págs. 1065–1148.
Pfenning, Frank (1996). "La práctica de los marcos lógicos". En Kirchner, H. (ed.). Árboles en álgebra y programación – CAAP '96 . Apuntes de clase en informática. Vol. 1059. Springer. págs. 119–134. doi :10.1007/3-540-61064-2_33. ISBN . 3-540-61064-2.
Constable, Robert L. (1998). "X. Tipos en informática, filosofía y lógica". En Buss, SR (ed.). Manual de teoría de la prueba . Estudios de lógica. Vol. 137. Elsevier. págs. 683–786. ISBN. 978-0-08-053318-6.
Wiedijk, Freek (2005). "Los diecisiete probadores del mundo" (PDF) . Universidad Radboud de Nimega.

Enlaces externos

Museo de Demostradores de Teoremas
"Introducción" a la Programación Certificada con Tipos Dependientes .
Introducción al Asistente de demostración Coq (con una introducción general a la demostración interactiva de teoremas)
Demostración interactiva de teoremas para usuarios de Agda
Una lista de herramientas para demostrar teoremas

Catálogos

Matemáticas digitales por categoría: Demostradores de tácticas
Sistemas y grupos de deducción automática
Sistemas de demostración de teoremas y razonamiento automático
Base de datos de sistemas de razonamiento mecanizado existentes
NuPRL: Otros sistemas
"Marcos lógicos específicos e implementaciones". Archivado desde el original el 10 de abril de 2022 . Consultado el 15 de febrero de 2024 .(Por Frank Pfenning).
DMOZ : Ciencias: Matemáticas: Lógica y fundamentos: Lógica computacional: Marcos lógicos

[1] Ornes, Stephen (27 de agosto de 2020). "Quanta Magazine – ¿Qué tan cerca están las computadoras de automatizar el razonamiento matemático?".

[2] Hunt, Warren; Matt Kaufmann; Robert Bellarmine Krug; J Moore; Eric W. Smith (2005). "Meta Reasoning in ACL2" (PDF) . Demostración de teoremas en lógica de orden superior . Apuntes de clase en informática. Vol. 3603. págs. 163–178. doi :10.1007/11541868_11. ISBN 978-3-540-28372-0.

[github-agda-3] "agda/agda: Agda es un lenguaje de programación de tipado dependiente / demostrador interactivo de teoremas". GitHub . Consultado el 31 de julio de 2024 .

[agdaWiki-4] "La Wiki de Agda" . Consultado el 31 de julio de 2024 .

[5] Buscar "pruebas por reflexión": arXiv :1803.06547

[6] "Página de lanzamientos de Lean 4". GitHub . Consultado el 15 de octubre de 2023 .

[7] "Versión v0.198 · metamath/Metamath-exe". GitHub .

[8] Farmer, William M.; Guttman, Joshua D.; Thayer, F. Javier (1993). "IMPS: Un sistema interactivo de prueba matemática". Journal of Automated Reasoning . 11 (2): 213–248. doi :10.1007/BF00881906. S2CID 3084322 . Consultado el 22 de enero de 2020 .

[9] "coq-community/vscoq". 29 de julio de 2024 – vía GitHub.

[10] Wenzel, Makarius. "Isabelle" . Consultado el 2 de noviembre de 2019 .

[11] "VS Code Lean 4". GitHub . Consultado el 15 de octubre de 2023 .

[12] Wiedijk, Freek (15 de septiembre de 2023). "Formalizando 100 teoremas".

[13] Geuvers, Herman (febrero de 2009). "Asistentes de prueba: Historia, ideas y futuro". Sādhanā . 34 (1): 3–25. doi : 10.1007/s12046-009-0001-5 . hdl : 2066/75958 . S2CID 14827467.

[14] Gonthier, Georges (2008), "Demostración formal: el teorema de los cuatro colores" (PDF) , Notices of the American Mathematical Society , 55 (11): 1382–1393, MR 2463991, archivado (PDF) desde el original el 2011-08-05

[15] "Feit Thomson demostró en Coq - Microsoft Research Inria Joint Centre". 19 de noviembre de 2016. Archivado desde el original el 19 de noviembre de 2016. Consultado el 7 de diciembre de 2023 .

[16] Licata, Daniel R.; Shulman, Michael (2013). "Cálculo del grupo fundamental del círculo en la teoría de tipos de homotopía". 28.° Simposio anual ACM/IEEE sobre lógica en informática de 2013. págs. 223–232. arXiv : 1301.3443 . doi :10.1109/lics.2013.28. ISBN 978-1-4799-0413-6. S2CID 5661377 . Consultado el 7 de diciembre de 2023 .

[17] "Un problema matemático que se ha estado desarrollando durante 3500 años finalmente obtiene una solución". IFLScience . 2022-03-11 . Consultado el 2024-02-09 .

[18] Avigad, Jeremy (2023). "Matemáticas y el giro formal". arXiv : 2311.00007 [math.HO].

[19] Sloman, Leila (6 de diciembre de 2023). "El 'Equipo A' de matemáticas demuestra un vínculo crítico entre la suma y los conjuntos". Revista Quanta . Consultado el 7 de diciembre de 2023 .

[20] "Hemos demostrado que "BB(5) = 47.176.870"". El desafío del castor atareado . 2024-07-02 . Consultado el 2024-07-09 .