Fórmula de masa semiempírica

Física nuclear
Núcleo Nucleones pag norte Materia nuclear Fuerza nuclear Estructura nuclear Reacción nuclear
Modelos del núcleo Gota de liquido Modelo de capa nuclear Modelo de bosón interactuante Desde el principio
Clasificación de los nucleidos Isótopos – iguales a Z Isóbaras – iguales A Isótonos – igual a N Isodiáferas – iguales N  −  Z Isómeros : son iguales a todos los anteriores. Núcleos espejo  – Z ↔ N Estable Magia Par/impar Halo Borromeo
Estabilidad nuclear Energía de unión relación p–n Línea de goteo Isla de estabilidad Valley of stability Stable nuclide
Radioactive decay Alpha α Beta β 2β 0v β+ K/L capture Isomeric Gamma γ Internal conversion Spontaneous fission Cluster decay Neutron emission Proton emission Decay energy Decay chain Decay product Radiogenic nuclide
Nuclear fission Spontaneous Products pair breaking Photofission
Capturing processes electron 2× neutron s r proton p rp
High-energy processes Spallation by cosmic ray Photodisintegration
Nucleosynthesis and nuclear astrophysics Nuclear fusion Processes: Stellar Big Bang Supernova Nuclides: Primordial Cosmogenic Artificial
High-energy nuclear physics Quark–gluon plasma RHIC LHC
Scientists Alvarez Becquerel Bethe A. Bohr N. Bohr Chadwick Cockcroft Ir. Curie Fr. Curie Pi. Curie Skłodowska-Curie Davisson Fermi Hahn Jensen Lawrence Mayer Meitner Oliphant Oppenheimer Proca Purcell Rabi Rutherford Soddy Strassmann Świątecki Szilárd Teller Thomson Walton Wigner
Physics portal  Category
v t e

En física nuclear , la fórmula de masa semiempírica ( SEMF ) (a veces también llamada fórmula de Weizsäcker , fórmula de Bethe-Weizsäcker o fórmula de masa de Bethe-Weizsäcker para distinguirla del proceso de Bethe-Weizsäcker ) se utiliza para aproximar la masa de un núcleo atómico a partir de su número de protones y neutrones . Como sugiere el nombre, se basa en parte en la teoría y en parte en mediciones empíricas . La fórmula representa el modelo de gota de líquido propuesto por George Gamow , ^[1] que puede explicar la mayoría de los términos de la fórmula y da estimaciones aproximadas de los valores de los coeficientes. Fue formulada por primera vez en 1935 por el físico alemán Carl Friedrich von Weizsäcker , ^[2] y aunque se han realizado mejoras en los coeficientes a lo largo de los años, la estructura de la fórmula sigue siendo la misma en la actualidad.

La fórmula proporciona una buena aproximación de las masas atómicas y, por lo tanto, de otros efectos. Sin embargo, no explica la existencia de líneas de mayor energía de enlace en determinadas cantidades de protones y neutrones. Estos números, conocidos como números mágicos , son la base del modelo de capas nucleares .

El modelo de gota de líquido fue propuesto por primera vez por George Gamow y desarrollado posteriormente por Niels Bohr , John Archibald Wheeler y Lise Meitner . ^[3] Trata al núcleo como una gota de fluido incompresible de muy alta densidad, que se mantiene unido por la fuerza nuclear (un efecto residual de la fuerza fuerte ), existe una similitud con la estructura de una gota de líquido esférica. Si bien es un modelo rudimentario, el modelo de gota de líquido tiene en cuenta la forma esférica de la mayoría de los núcleos y realiza una predicción aproximada de la energía de enlace.

La fórmula de masa correspondiente se define únicamente en términos de la cantidad de protones y neutrones que contiene. La fórmula original de Weizsäcker define cinco términos:

• Energía volumétrica : cuando un conjunto de nucleones del mismo tamaño se agrupa en un volumen mínimo, cada nucleón interior tiene una cierta cantidad de otros nucleones en contacto con él. Por lo tanto, esta energía nuclear es proporcional al volumen.
• La energía superficial corrige la suposición anterior de que cada nucleón interactúa con el mismo número de otros nucleones. Este término es negativo y proporcional al área superficial y, por lo tanto, es aproximadamente equivalente a la tensión superficial del líquido .
• Energía de Coulomb , la energía potencial de cada par de protones. Como se trata de una fuerza de repulsión, la energía de enlace se reduce.
• Energía de asimetría (también llamada energía de Pauli ), que explica el principio de exclusión de Pauli . Un número desigual de neutrones y protones implica que se llenan los niveles de energía más altos para un tipo de partícula, mientras que los niveles de energía más bajos quedan vacíos para el otro tipo.
• Energía de apareamiento , que explica la tendencia a la formación de pares de protones y neutrones . Un número par de partículas es más estable que un número impar debido al acoplamiento de espín .

La masa de un núcleo atómico, para neutrones , protones y, por lo tanto, nucleones , viene dada por${\displaystyle N}$ ${\displaystyle Z}$ ${\displaystyle A=N+Z}$

${\displaystyle m=Zm_{H_{1}}+Nm_{\text{n}}-{\frac {E_{\text{B}}(N,Z)}{c^{2}}},}$

donde y son la masa en reposo de un protón y un neutrón respectivamente, y es la energía de enlace del núcleo. La fórmula de masa semiempírica establece que la energía de enlace es ^[4]${\displaystyle m_{\text{p}}}$${\displaystyle m_{\text{n}}}$${\displaystyle E_{\text{B}}}$

${\displaystyle E_{\text{B}}=a_{\text{V}}A-a_{\text{S}}A^{2/3}-a_{\text{C}}{\frac {Z(Z-1)}{A^{1/3}}}-a_{\text{A}}{\frac {(N-Z)^{2}}{A}}\pm \delta (N,Z).}$

El término es cero o , dependiendo de la paridad de y , donde para algún exponente . Nótese que como , el numerador del término puede reescribirse como .${\displaystyle \delta (N,Z)}$${\displaystyle \pm \delta _{0}}$${\displaystyle N}$${\displaystyle Z}$${\displaystyle \delta _{0}={a_{\text{P}}}{A^{k_{\text{P}}}}}$${\displaystyle k_{\text{P}}}$${\displaystyle A=N+Z}$${\displaystyle a_{\text{A}}}$${\displaystyle (A-2Z)^{2}}$

Cada uno de los términos de esta fórmula tiene una base teórica. Los coeficientes , , , y se determinan empíricamente; si bien pueden derivarse de experimentos, generalmente se derivan de un ajuste de mínimos cuadrados a datos contemporáneos. Si bien generalmente se expresa mediante sus cinco términos básicos, existen otros términos para explicar fenómenos adicionales. De manera similar a cómo cambiar un ajuste polinomial cambiará sus coeficientes, la interacción entre estos coeficientes a medida que se introducen nuevos fenómenos es compleja; algunos términos se influyen entre sí, mientras que el término es en gran medida independiente. ^[5]${\displaystyle a_{\text{V}}}$${\displaystyle a_{\text{S}}}$${\displaystyle a_{\text{C}}}$${\displaystyle a_{\text{A}}}$${\displaystyle a_{\text{P}}}$${\displaystyle a_{\text{P}}}$

El término se conoce como término de volumen . El volumen del núcleo es proporcional a A , por lo que este término es proporcional al volumen, de ahí el nombre.${\displaystyle a_{\text{V}}A}$

La base de este término es la fuerza nuclear fuerte . La fuerza fuerte afecta tanto a los protones como a los neutrones y, como se esperaba, este término es independiente de Z. Debido a que el número de pares que se pueden tomar de las partículas A es , se podría esperar un término proporcional a . Sin embargo, la fuerza fuerte tiene un rango muy limitado y un nucleón dado solo puede interactuar fuertemente con sus vecinos más cercanos y los vecinos más próximos. Por lo tanto, el número de pares de partículas que realmente interactúan es aproximadamente proporcional a A , lo que le da al término de volumen su forma.${\displaystyle A(A-1)/2}$${\displaystyle A^{2}}$

El coeficiente es menor que la energía de enlace que poseen los nucleones con respecto a sus vecinos ( ), que es del orden de 40  MeV . Esto se debe a que cuanto mayor es el número de nucleones en el núcleo, mayor es su energía cinética, debido al principio de exclusión de Pauli . Si uno trata al núcleo como una bola de Fermi de nucleones , con igual número de protones y neutrones, entonces la energía cinética total es , con la energía de Fermi , que se estima en 38  MeV . Por lo tanto, el valor esperado de en este modelo no está lejos del valor medido.${\displaystyle a_{\text{V}}}$${\displaystyle E_{\text{b}}}$${\displaystyle A}$ ${\displaystyle {\tfrac {3}{5}}A\varepsilon _{\text{F}}}$${\displaystyle \varepsilon _{\text{F}}}$${\displaystyle a_{\text{V}}}$${\displaystyle E_{\text{b}}-{\tfrac {3}{5}}\varepsilon _{\text{F}}\sim 17~\mathrm {MeV} ,}$

El término se conoce como término de superficie . Este término, también basado en la fuerza fuerte, es una corrección del término de volumen.${\displaystyle a_{\text{S}}A^{2/3}}$

El término de volumen sugiere que cada nucleón interactúa con un número constante de nucleones, independientemente de A . Si bien esto es casi cierto para los nucleones que se encuentran en las profundidades del núcleo, los nucleones que se encuentran en la superficie del núcleo tienen menos vecinos más cercanos, lo que justifica esta corrección. Esto también puede considerarse un término de tensión superficial y, de hecho, un mecanismo similar crea tensión superficial en los líquidos.

Si el volumen del núcleo es proporcional a A , entonces el radio debería ser proporcional a y el área superficial a . Esto explica por qué el término de superficie es proporcional a . También se puede deducir que debería tener un orden de magnitud similar a .${\displaystyle A^{1/3}}$${\displaystyle A^{2/3}}$${\displaystyle A^{2/3}}$${\displaystyle a_{\text{S}}}$${\displaystyle a_{\text{V}}}$

El término o se conoce como término de Coulomb o electrostático .${\displaystyle a_{\text{C}}{\frac {Z(Z-1)}{A^{1/3}}}}$${\displaystyle a_{\text{C}}{\frac {Z^{2}}{A^{1/3}}}}$

La base de este término es la repulsión electrostática entre protones. En una aproximación muy aproximada, el núcleo puede considerarse una esfera de densidad de carga uniforme. Se puede demostrar que la energía potencial de dicha distribución de carga es

${\displaystyle E={\frac {3}{5}}{\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q^{2}}{R}},}$

donde Q es la carga total y R es el radio de la esfera. El valor de se puede calcular de forma aproximada utilizando esta ecuación para calcular la energía potencial, utilizando un radio nuclear empírico de y Q = Ze . Sin embargo, debido a que la repulsión electrostática solo existirá para más de un protón, se convierte en :${\displaystyle a_{\text{C}}}$${\displaystyle R\approx r_{0}A^{\frac {1}{3}}}$${\displaystyle Z^{2}}$${\displaystyle Z(Z-1)}$

${\displaystyle E={\frac {3}{5}}{\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q^{2}}{R}}={\frac {3}{5}}{\frac {1}{4\pi \varepsilon _{0}}}{\frac {(Ze)^{2}}{r_{0}A^{1/3}}}={\frac {3e^{2}Z^{2}}{20\pi \varepsilon _{0}r_{0}A^{1/3}}}\approx {\frac {3e^{2}Z(Z-1)}{20\pi \varepsilon _{0}r_{0}A^{1/3}}}=a_{\text{C}}{\frac {Z(Z-1)}{A^{1/3}}},}$

donde ahora la constante electrostática de Coulomb es${\displaystyle a_{\text{C}}}$

${\displaystyle a_{\text{C}}={\frac {3e^{2}}{20\pi \varepsilon _{0}r_{0}}}.}$

Usando la constante de estructura fina , podemos reescribir el valor de como${\displaystyle a_{\text{C}}}$

${\displaystyle a_{\text{C}}={\frac {3}{5}}{\frac {\hbar c\alpha }{r_{0}}}={\frac {3}{5}}{\frac {R_{\text{P}}}{r_{0}}}\alpha m_{\text{p}}c^{2},}$

donde es la constante de estructura fina, y es el radio de un núcleo , lo que da aproximadamente 1,25  femtómetros . es la longitud de onda Compton reducida del protón y es la masa del protón. Esto da un valor teórico aproximado de 0,691  MeV , no muy alejado del valor medido.${\displaystyle \alpha }$${\displaystyle r_{0}A^{1/3}}$${\displaystyle r_{0}}$${\displaystyle R_{\text{P}}}$${\displaystyle m_{\text{p}}}$${\displaystyle a_{\text{C}}}$

El término se conoce como término de asimetría (o término de Pauli ).${\displaystyle a_{\text{A}}{\frac {(N-Z)^{2}}{A}}}$

La justificación teórica de este término es más compleja. El principio de exclusión de Pauli establece que no pueden existir dos fermiones idénticos que ocupen exactamente el mismo estado cuántico en un átomo. En un nivel de energía determinado, solo hay un número finito de estados cuánticos disponibles para las partículas. Lo que esto significa en el núcleo es que a medida que se "agregan" más partículas, estas deben ocupar niveles de energía más altos, lo que aumenta la energía total del núcleo (y disminuye la energía de enlace). Nótese que este efecto no se basa en ninguna de las fuerzas fundamentales ( gravitatoria , electromagnética, etc.), solo en el principio de exclusión de Pauli.

Los protones y los neutrones, al ser tipos distintos de partículas, ocupan estados cuánticos diferentes. Se puede pensar en dos "grupos" de estados diferentes: uno para los protones y otro para los neutrones. Ahora bien, por ejemplo, si hay significativamente más neutrones que protones en un núcleo, algunos de los neutrones tendrán una energía mayor que los estados disponibles en el grupo de protones. Si pudiéramos mover algunas partículas del grupo de neutrones al grupo de protones, en otras palabras, convertir algunos neutrones en protones, disminuiríamos significativamente la energía. El desequilibrio entre el número de protones y neutrones hace que la energía sea mayor de lo que debería ser, para un número dado de nucleones . Esta es la base del término de asimetría.

La forma real del término de asimetría se puede derivar nuevamente modelando el núcleo como una bola de Fermi de protones y neutrones. Su energía cinética total es

${\displaystyle E_{\text{k}}={\frac {3}{5}}(Z\varepsilon _{\text{F,p}}+N\varepsilon _{\text{F,n}}),}$

donde y son las energías de Fermi de los protones y neutrones. Como son proporcionales a y respectivamente, se obtiene${\displaystyle \varepsilon _{\text{F,p}}}$${\displaystyle \varepsilon _{\text{F,n}}}$${\displaystyle Z^{2/3}}$${\displaystyle N^{2/3}}$

${\displaystyle E_{\text{k}}=C(Z^{5/3}+N^{5/3})}$para alguna constante C.

Los términos principales en la expansión en la diferencia son entonces${\displaystyle N-Z}$

${\displaystyle E_{\text{k}}={\frac {C}{2^{2/3}}}\left(A^{5/3}+{\frac {5}{9}}{\frac {(N-Z)^{2}}{A^{1/3}}}\right)+O{\big (}(N-Z)^{4}{\big )}.}$

En el orden cero de la expansión, la energía cinética es simplemente la energía total de Fermi multiplicada por . Por lo tanto, obtenemos${\displaystyle \varepsilon _{\text{F}}\equiv \varepsilon _{\text{F,p}}=\varepsilon _{\text{F,n}}}$${\displaystyle {\tfrac {3}{5}}A}$

${\displaystyle E_{\text{k}}={\frac {3}{5}}\varepsilon _{\text{F}}A+{\frac {1}{3}}\varepsilon _{\text{F}}{\frac {(N-Z)^{2}}{A}}+O{\big (}(N-Z)^{4}{\big )}.}$

El primer término contribuye al término de volumen en la fórmula de masa semiempírica, y el segundo término es menos el término de asimetría (recuerde, la energía cinética contribuye a la energía de enlace total con un signo negativo ).

${\displaystyle \varepsilon _{\text{F}}}$es 38 MeV , por lo que calculando a partir de la ecuación anterior, obtenemos solo la mitad del valor medido. La discrepancia se explica por que nuestro modelo no es preciso: de hecho, los nucleones interactúan entre sí y no se distribuyen uniformemente por el núcleo. Por ejemplo, en el modelo de capas , un protón y un neutrón con funciones de onda superpuestas tendrán una mayor interacción fuerte entre ellos y una energía de enlace más fuerte. Esto hace que sea energéticamente favorable (es decir, que tengan menor energía) que los protones y los neutrones tengan los mismos números cuánticos (aparte del isospín ), y por lo tanto aumente el costo energético de la asimetría entre ellos.${\displaystyle a_{\text{A}}}$

También se puede entender el término de asimetría intuitivamente de la siguiente manera. Debería depender de la diferencia absoluta y la forma es simple y diferenciable , lo que es importante para ciertas aplicaciones de la fórmula. Además, las pequeñas diferencias entre Z y N no tienen un alto costo energético. La A en el denominador refleja el hecho de que una diferencia dada es menos significativa para valores mayores de A.${\displaystyle |N-Z|}$${\displaystyle (N-Z)^{2}}$${\displaystyle |N-Z|}$

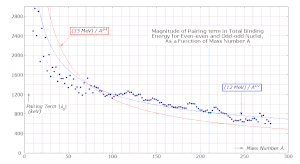
El término se conoce como término de emparejamiento (posiblemente también conocido como interacción por pares). Este término captura el efecto del acoplamiento de espín . Está dado por ^[7]${\displaystyle \delta (A,Z)}$

${\displaystyle \delta (A,Z)={\begin{cases}+\delta _{0}&{\text{for even }}Z,N~({\text{even }}A),\\0&{\text{for odd }}A,\\-\delta _{0}&{\text{for odd }}Z,N~({\text{even }}A),\end{cases}}}$

donde se encuentra empíricamente que tiene un valor de aproximadamente 1000 keV, disminuyendo lentamente con el número de masa  A . La energía de enlace se puede aumentar convirtiendo uno de los protones o neutrones impares en un neutrón o protón, por lo que el nucleón impar puede formar un par con su vecino impar formando ^{[ aclaración necesaria ]} y par Z , N . Los pares tienen funciones de onda superpuestas y se sientan muy cerca uno del otro con un enlace más fuerte que cualquier otra configuración. ^[7] Cuando el término de emparejamiento se sustituye en la ecuación de energía de enlace, para Z , N par , el término de emparejamiento agrega energía de enlace, y para Z , N impar el término de emparejamiento elimina energía de enlace.${\displaystyle \delta _{0}}$

La dependencia del número de masa se parametriza comúnmente como

${\displaystyle \delta _{0}=a_{\text{P}}A^{k_{\text{P}}}.}$

El valor del exponente k _P se determina a partir de datos experimentales de energía de enlace. En el pasado, se suponía que su valor era −3/4, pero los datos experimentales modernos indican que un valor de −1/2 es más cercano a la realidad:

${\displaystyle \delta _{0}=a_{\text{P}}A^{-1/2}}$o${\displaystyle \delta _{0}=a_{\text{P}}A^{-3/4}.}$

Debido al principio de exclusión de Pauli, el núcleo tendría una energía menor si el número de protones con espín hacia arriba fuera igual al número de protones con espín hacia abajo. Esto también es cierto para los neutrones. Solo si Z y N son pares, tanto los protones como los neutrones pueden tener el mismo número de partículas con espín hacia arriba y hacia abajo. Este es un efecto similar al término de asimetría.

El factor no se explica fácilmente teóricamente. El cálculo de la bola de Fermi que hemos utilizado anteriormente, basado en el modelo de gota de líquido pero ignorando las interacciones, dará una dependencia, como en el término de asimetría. Esto significa que el efecto real para núcleos grandes será mayor que el esperado por ese modelo. Esto debería explicarse por las interacciones entre nucleones. Por ejemplo, en el modelo de capas , dos protones con los mismos números cuánticos (excepto el espín ) tendrán funciones de onda completamente superpuestas y, por lo tanto, tendrán una mayor interacción fuerte entre ellos y una energía de enlace más fuerte. Esto hace que sea energéticamente favorable (es decir, que tenga menor energía) que los protones formen pares de espín opuesto. Lo mismo es cierto para los neutrones.${\displaystyle A^{k_{\text{P}}}}$${\displaystyle A^{-1}}$

Los coeficientes se calculan ajustándolos a masas de núcleos medidas experimentalmente. Sus valores pueden variar según cómo se ajusten a los datos y qué unidad se utilice para expresar la masa. A continuación se muestran varios ejemplos.

	Eisberg y Resnick [8]	Ajuste por mínimos cuadrados (1)	Ajuste por mínimos cuadrados (2) [9]	Rohlf [10]	Wapstra [11]
unidad	tú	MeV	MeV	MeV	MeV
${\displaystyle a_{\rm {V}}}$	0,01691	15.8	15,76	15,75	14.1
${\displaystyle a_{\rm {S}}}$	0,01911	18.3	17.81	17.8	13
${\displaystyle a_{\rm {C}}}$	0,000763 [α]	0,714	0,711	0,711	0,595
${\displaystyle a_{\rm {A}}}$	0,10175 [β]	23.2	23.702	23.7	19
${\displaystyle a_{\rm {P}}}$	0,012	12	34	11.18	33.5
${\displaystyle k_{\rm {P}}}$	-1/2	-1/2	-3/4	-1/2	-3/4
${\displaystyle \delta _{0}}$(par-par)	${\displaystyle -0.012 \over A^{1/2}}$	${\displaystyle +12 \over A^{1/2}}$	${\displaystyle +34 \over A^{3/4}}$	${\displaystyle +11.18 \over A^{1/2}}$	${\displaystyle +33.5 \over A^{3/4}}$
${\displaystyle \delta _{0}}$(impar-impar)	${\displaystyle +0.012 \over A^{1/2}}$	${\displaystyle -12 \over A^{1/2}}$	${\displaystyle -34 \over A^{3/4}}$	${\displaystyle -11.18 \over A^{1/2}}$	${\displaystyle -33.5 \over A^{3/4}}$
${\displaystyle \delta _{0}}$(par-impar, impar-par)	0	0	0	0	0
^ Este modelo utiliza en el numerador el término de Coulomb.${\displaystyle Z^{2}}$ ^ Este modelo utiliza en el numerador el término Asimetría.${\displaystyle (Z-A/2)^{2}}$

La fórmula no tiene en cuenta la estructura interna del núcleo.

Por lo tanto, la fórmula de masa semiempírica proporciona un buen ajuste para los núcleos más pesados ​​y un mal ajuste para los núcleos muy ligeros, especialmente ⁴ He . Para los núcleos ligeros, suele ser mejor utilizar un modelo que tenga en cuenta esta estructura de capas.

Al maximizar E _b ( A , Z ) con respecto a Z , se encontraría la mejor relación neutrón-protón N / Z para un peso atómico dado A . ^[10] Obtenemos

${\displaystyle N/Z\approx 1+{\frac {a_{\text{C}}}{2a_{\text{A}}}}A^{2/3}.}$

Esto es aproximadamente 1 para los núcleos ligeros, pero para los núcleos pesados ​​la relación crece de acuerdo con el experimento .

Sustituyendo el valor anterior de Z en E _b , se obtiene la energía de enlace en función del peso atómico, E _b ( A ) . Maximizando E _b ( A )/ A con respecto a A se obtiene el núcleo que está más fuertemente unido, es decir, el más estable. El valor que obtenemos es A = 63 ( cobre ), cercano a los valores medidos de A = 62 ( níquel ) y A = 58 ( hierro ).

El modelo de gota líquida también permite el cálculo de barreras de fisión para núcleos, que determinan la estabilidad de un núcleo contra la fisión espontánea . Originalmente se especuló que los elementos más allá del número atómico 104 no podrían existir, ya que sufrirían fisión con vidas medias muy cortas, ^[12] aunque esta fórmula no consideró los efectos estabilizadores de las capas nucleares cerradas . Una fórmula modificada que considera los efectos de las capas reproduce los datos conocidos y la isla de estabilidad predicha (en la que se espera que las barreras de fisión y las vidas medias aumenten, alcanzando un máximo en los cierres de las capas), aunque también sugiere un posible límite a la existencia de núcleos superpesados ​​más allá de Z  =  120 y N  = 184. ^[12]

• Freedman, R.; Young, H. (2004). Física universitaria de Sears y Zemansky con física moderna (11.ª ed.). Pearson Addison Wesley. págs. 1633–1634. ISBN 978-0-8053-8768-1.
• Liverhant, SE (1960). Introducción elemental a la física de reactores nucleares . John Wiley & Sons . págs. 58–62. LCCN  60011725.
• Choppin, G.; Liljenzin, J.-O.; Rydberg, J. (2002). "Masa nuclear y estabilidad" (PDF) . Radioquímica y química nuclear (3.ª ed.). Butterworth-Heinemann . págs. 41–57. ISBN. 978-0-7506-7463-8.

• Modelo de gota de líquido nuclear en la referencia en línea de hiperfísica de la Universidad Estatal de Georgia .
• Modelo de gota de líquido con ajuste de parámetros de las Primeras observaciones de estados excitados en los núcleos deficientes en neutrones ^{160, 161} W y ¹⁵⁹ Ta , Alex Keenan, tesis doctoral, Universidad de Liverpool , 1999 (versión HTML).