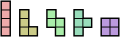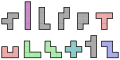Poliominó
Formas geométricas formadas a partir de cuadrados.
Los 18 pentominós unilaterales , incluidos 6 pares reflejados.

Un poliominó es una figura geométrica plana formada por la unión de uno o más cuadrados iguales borde con borde. Es una poliforma cuyas celdas son cuadrados. Puede considerarse como un subconjunto finito del mosaico de cuadrados regulares .

Los poliominós se han utilizado en los juegos de mesa populares desde al menos 1907, y la enumeración de los pentominós data de la antigüedad. [1] Muchos resultados con piezas de 1 a 6 casillas fueron publicados por primera vez en Fairy Chess Review entre los años 1937 y 1957, bajo el nombre de "problemas de disección". El nombre poliominó fue inventado por Solomon W. Golomb en 1953, [2] y fue popularizado por Martin Gardner en una columna de " Juegos matemáticos " de noviembre de 1960 en Scientific American . [3]

Los poliominós están relacionados con los polidiamantes , formados a partir de triángulos equiláteros ; los polihexágonos , formados a partir de hexágonos regulares ; y otras poliformas planas . Los poliominós se han generalizado a dimensiones superiores uniendo cubos para formar policubos , o hipercubos para formar polihipercubos.

En física estadística , el estudio de los poliominós y sus análogos de dimensiones superiores (que a menudo se denominan animales reticulares en esta literatura) se aplica a problemas de física y química. Los poliominós se han utilizado como modelos de polímeros ramificados y de cúmulos de percolación . [4]

Al igual que muchos acertijos de las matemáticas recreativas , los poliominós plantean muchos problemas combinatorios . El más básico es enumerar poliominós de un tamaño determinado. No se ha encontrado ninguna fórmula, excepto para clases especiales de poliominós. Se conocen varias estimaciones y existen algoritmos para calcularlas.

Los poliominós con agujeros resultan poco prácticos para algunos propósitos, como los problemas de teselación. En algunos contextos, se excluyen los poliominós con agujeros y solo se permiten poliominós conexos simples . [5]

Enumeración de poliominós

Poliominós libres, unilaterales y fijos

Hay tres formas comunes de distinguir poliominós para enumeración: [6] [7]

  • Los poliominós libres se distinguen cuando ninguno es una transformación rígida ( traslación , rotación , reflexión o reflexión por deslizamiento ) de otro (piezas que se pueden levantar y dar vuelta). Trasladar, rotar, reflejar o reflejar por deslizamiento un poliominó libre no cambia su forma.
  • Los poliominós unilaterales se distinguen cuando ninguno de ellos es una traslación o rotación de otro (piezas que no se pueden voltear). Trasladar o rotar un poliominó unilateral no cambia su forma.
  • Los poliominós fijos son distintos cuando ninguno es una traslación de otro (piezas que no se pueden voltear ni rotar). Trasladar un poliominó fijo no cambiará su forma.

La siguiente tabla muestra el número de poliominós de varios tipos con n celdas.

nortenombregratisunilateralfijado
totalcon agujerosSin agujeros
1monomino10111
2dominó10112
3Trombón20226
4tetrominó505719
5pentominó120121863
6hexominó3503560216
7heptomino1081107196760
8octominó36963637042.725
9no-nomino1.285371.2482.5009,910
10decomino4.6551954.4609,18936.446
11descomino17.07397916.09433.896135.268
12dodecomino63.6004.66358,937126.759505.861
 Secuencia OEISA000105A001419A000104A000988A001168

Los poliominós fijos fueron enumerados en 2004 hasta n = 56 por Iwan Jensen, [8] y en 2024 hasta n = 70 por Gill Barequet y Gil Ben-Shachar. [9]

Los poliominós libres fueron enumerados en 2007 hasta n = 28 por Tomás Oliveira e Silva [10] , en 2012 hasta n = 45 por Toshihiro Shirakawa [11] y en 2023 hasta n = 50 por John Mason. [12]

Las secuencias OEIS anteriores, con excepción de A001419, incluyen el recuento de 1 para el número de poliominós nulos; un poliominó nulo es uno que está formado por cero cuadrados.

Simetrías de poliominós

El grupo diedro D 4 es el grupo de simetrías ( grupo de simetría ) de un cuadrado. Este grupo contiene cuatro rotaciones y cuatro reflexiones. Se genera alternando reflexiones sobre el eje x y sobre una diagonal. Un poliominó libre corresponde a un máximo de 8 poliominós fijos, que son sus imágenes bajo las simetrías de D 4 . Sin embargo, esas imágenes no son necesariamente distintas: cuanto más simetría tenga un poliominó libre, menos contrapartes fijas distintas tendrá. Por lo tanto, un poliominó libre que sea invariante bajo algunas o todas las simetrías no triviales de D 4 puede corresponder a solo 4, 2 o 1 poliominó fijo. Matemáticamente, los poliominós libres son clases de equivalencia de poliominós fijos bajo el grupo D 4 .

Los poliominós tienen las siguientes simetrías posibles; [13] el menor número de cuadrados necesarios en un poliominó con esa simetría se da en cada caso:

  • 8 poliominós fijos por cada poliominó libre:
    • Sin simetría (4)
  • 4 poliominós fijos por cada poliominó libre:
    • simetría especular con respecto a una de las direcciones de la línea de la cuadrícula (4)
    • simetría especular con respecto a una línea diagonal (3)
    • Simetría rotacional doble: C 2 (4)
  • 2 poliominós fijos por cada poliominó libre:
    • simetría con respecto a ambas direcciones de la línea de la cuadrícula y, por lo tanto, también simetría rotacional doble: D 2 (2) (también conocido como el grupo de cuatro de Klein )
    • simetría con respecto a ambas direcciones diagonales y, por lo tanto, también simetría rotacional doble: D 2 (7)
    • Simetría rotacional cuádruple: C 4 (8)
  • 1 poliominó fijo por cada poliominó libre:
    • Toda simetría del cuadrado: D 4 (1).

De la misma manera, el número de poliominós unilaterales depende de la simetría del poliominó de la siguiente manera:

  • 2 poliominós unilaterales por cada poliominó libre:
    • Sin simetría
    • Simetría rotacional doble: C 2
    • Simetría rotacional cuádruple: C 4
  • 1 poliominó unilateral por cada poliominó libre:
    • Toda simetría del cuadrado: D 4
    • Simetría especular con respecto a una de las direcciones de la línea de la cuadrícula
    • Simetría especular con respecto a una línea diagonal
    • simetría con respecto a ambas direcciones de la línea de la cuadrícula y, por lo tanto, también simetría rotacional doble: D 2
    • simetría con respecto a ambas direcciones diagonales y, por lo tanto, también simetría rotacional doble: D 2 .

La siguiente tabla muestra el número de poliominós con n cuadrados, ordenados por grupos de simetría.

norteningunoespejo
de 90°		espejo
45°		C 2D2 90 °
D2 45
°		C 4D4​
100000001
200001000
300101000
411011001
552211001
6206252000
7849743100
8316235184111
91.1963826194002
104.4619022738100
1116.750147917310200
1262.8783417927815333
 Secuencia OEISA006749A006746A006748A006747A056877A056878A144553A142886

[14]

Algoritmos para la enumeración de poliominós fijos

Algoritmos inductivos

Cada poliominó de tamaño n +1 se puede obtener sumando un cuadrado a un poliominó de tamaño n . Esto conduce a algoritmos para generar poliominós de manera inductiva.

En términos más simples, dada una lista de poliominós de tamaño n , se pueden agregar cuadrados al lado de cada poliominó en cada posición posible, y el poliominó resultante de tamaño n +1 se agrega a la lista si no es un duplicado de uno ya encontrado; los refinamientos en el orden de la enumeración y el marcado de cuadrados adyacentes que no se deben considerar reducen la cantidad de casos que se deben verificar en busca de duplicados. [15] Este método se puede utilizar para enumerar poliominós libres o fijos.

Muchos autores han utilizado un método más sofisticado, descrito por Redelmeier, como una forma no solo de contar poliominós (sin requerir que todos los poliominós de tamaño n se almacenen en tamaño para enumerar los de tamaño n +1), sino también para demostrar límites superiores en su número. La idea básica es que comenzamos con un solo cuadrado y, a partir de allí, agregamos cuadrados recursivamente. Dependiendo de los detalles, puede contar cada n -ómino n veces, una vez a partir de cada uno de sus n cuadrados, o puede estar organizado para contar cada uno solo una vez.

La implementación más simple implica agregar un cuadrado a la vez. Comenzando con un cuadrado inicial, numere los cuadrados adyacentes, en el sentido de las agujas del reloj desde arriba, 1, 2, 3 y 4. Ahora elija un número entre 1 y 4 y agregue un cuadrado en esa ubicación. Numere los cuadrados adyacentes sin numerar, comenzando con 5. Luego, elija un número mayor que el número elegido anteriormente y agregue ese cuadrado. Continúe eligiendo un número mayor que el número del cuadrado actual, agregue ese cuadrado y luego numere los nuevos cuadrados adyacentes. Cuando se hayan creado n cuadrados, se habrá creado un n -ómino.

Este método garantiza que cada poliominó fijo se cuente exactamente n veces, una por cada cuadrado inicial. Se puede optimizar para que cuente cada poliominó solo una vez, en lugar de n veces. Comenzando con el cuadrado inicial, declare que es el cuadrado inferior izquierdo del poliominó. Simplemente no numere ningún cuadrado que esté en una fila inferior o a la izquierda del cuadrado en la misma fila. Esta es la versión descrita por Redelmeier.

Si en cambio se desea contar poliominós libres, se pueden verificar las simetrías después de crear cada n -ominó. Sin embargo, es más rápido [16] generar poliominós simétricos por separado (mediante una variación de este método) [17] y así determinar el número de poliominós libres mediante el lema de Burnside .

Método de la matriz de transferencia

El algoritmo más moderno para enumerar los poliominós fijos fue descubierto por Iwan Jensen. [18] Es una mejora del método de Andrew Conway, [19] es exponencialmente más rápido que los métodos anteriores (sin embargo, su tiempo de ejecución sigue siendo exponencial en n ).

Tanto la versión de Conway como la de Jensen del método de la matriz de transferencia implican contar el número de poliominós que tienen un ancho determinado. Calcular el número para todos los anchos da el número total de poliominós. La idea básica detrás del método es que se consideran las posibles filas iniciales y luego se determina el número mínimo de cuadrados necesarios para completar el poliominó del ancho dado. Combinada con el uso de funciones generadoras , esta técnica puede contar muchos poliominós a la vez, lo que le permite ejecutarse mucho más rápido que los métodos que tienen que generar cada poliominó.

Si bien tiene un excelente tiempo de ejecución, la desventaja es que este algoritmo utiliza cantidades exponenciales de memoria (se necesitan muchos gigabytes de memoria para n por encima de 50), es mucho más difícil de programar que los otros métodos y actualmente no se puede usar para contar poliominós libres.

Crecimiento asintótico del número de poliominós

Poliominós fijos

Argumentos teóricos y cálculos numéricos respaldan la estimación del número de poliominós fijos de tamaño n

A norte ∼ do la norte norte {\displaystyle A_{n}\sim {\frac {c\lambda ^{n}}{n}}}

donde λ = 4,0626 y c = 0,3169. [20] Sin embargo, este resultado no está probado y los valores de λ y c son solo estimaciones.

Los resultados teóricos conocidos no son tan específicos como esta estimación. Se ha demostrado que

límite norte → ∞ ( A norte ) 1 norte = la {\displaystyle \lim_{n\rightarrow \infty}(A_{n})^{\frac {1}{n}}=\lambda}

existe. En otras palabras, A n crece exponencialmente . El límite inferior más conocido para λ , encontrado en 2016, es 4.00253. [21] El límite superior más conocido es λ < 4.5252 . [22]

Para establecer un límite inferior, un método simple pero altamente efectivo es la concatenación de poliominós. Defina el cuadrado superior derecho como el cuadrado más a la derecha en la fila superior del poliominó. Defina el cuadrado inferior izquierdo de manera similar. Luego, el cuadrado superior derecho de cualquier poliominó de tamaño n se puede unir al cuadrado inferior izquierdo de cualquier poliominó de tamaño m para producir un ( n + m )-ominó único. Esto demuestra que A n A m ≤ A n + m . Usando esta ecuación, uno puede mostrar λ ≥ ( A n ) 1/ n para todo n . Los refinamientos de este procedimiento combinados con datos para A n producen el límite inferior dado anteriormente.

El límite superior se obtiene generalizando el método inductivo de enumeración de poliominós. En lugar de sumar un cuadrado a la vez, se suman un grupo de cuadrados a la vez. Esto se suele describir como sumar ramitas . Al demostrar que cada n -ominó es una secuencia de ramitas, y al demostrar límites a las combinaciones de ramitas posibles, se obtiene un límite superior al número de n -ominós. Por ejemplo, en el algoritmo descrito anteriormente, en cada paso debemos elegir un número mayor, y como máximo se añaden tres números nuevos (ya que como máximo tres cuadrados no numerados son adyacentes a cualquier cuadrado numerado). Esto se puede utilizar para obtener un límite superior de 6,75. Utilizando 2,8 millones de ramitas, Klarner y Rivest obtuvieron un límite superior de 4,65, [23] que posteriormente fue mejorado por Barequet y Shalah a 4,5252. [22]

Poliominós libres

Las aproximaciones para el número de poliominós fijos y poliominós libres están relacionadas de una manera simple. Un poliominó libre sin simetrías (rotación o reflexión) corresponde a 8 poliominós fijos distintos, y para n grande , la mayoría de los n -ominós no tienen simetrías. Por lo tanto, el número de n -ominós fijos es aproximadamente 8 veces el número de n -ominós libres. Además, esta aproximación es exponencialmente más precisa a medida que n aumenta. [13]

Clases especiales de poliominós

Se conocen fórmulas exactas para enumerar poliominós de clases especiales, como la clase de poliominós convexos y la clase de poliominós dirigidos .

La definición de un poliominó convexo es diferente de la definición habitual de convexidad , pero es similar a la definición utilizada para la envoltura convexa ortogonal . Se dice que un poliominó es convexo vertical o en columna si su intersección con cualquier línea vertical es convexa (en otras palabras, cada columna no tiene agujeros). De manera similar, se dice que un poliominó es convexo horizontal o en fila si su intersección con cualquier línea horizontal es convexa. Se dice que un poliominó es convexo si es convexo en fila y columna. [24]

Se dice que un poliominó está dirigido si contiene un cuadrado, conocido como raíz , tal que se puede llegar a cualquier otro cuadrado con movimientos de un cuadrado hacia arriba o hacia la derecha, sin salir del poliominó.

Los poliominós dirigidos, [25] poliominós convexos de columna (o fila), [26] y poliominós convexos [27] se han enumerado de manera efectiva por área n , así como por algunos otros parámetros como el perímetro, utilizando funciones generadoras .

Un poliominó es igual si su área es igual a su perímetro. Un poliominó igual debe estar formado por un número par de cuadrados; todo número par mayor que 15 es posible. Por ejemplo, el 16-ominó en forma de cuadrado de 4 × 4 y el 18-ominó en forma de rectángulo de 3 × 6 son ambos iguales. Para los poliominós con 15 cuadrados o menos, el perímetro siempre excede el área. [28]

Teselación con poliominós

En matemáticas recreativas , a menudo se plantean desafíos para cubrir una región prescrita, o todo el plano, con poliominós, [29] y los problemas relacionados se investigan en matemáticas y ciencias de la computación .

Teselación de regiones con conjuntos de poliominós

Los acertijos suelen pedir que se embaldose una región dada con un conjunto dado de poliominós, como los 12 pentominós. Los libros de Golomb y Gardner tienen muchos ejemplos. Un acertijo típico es el de embaldosar un rectángulo de 6×10 con los doce pentominós; las 2339 soluciones para esto se encontraron en 1960. [30] Cuando se permiten múltiples copias de los poliominós en el conjunto, Golomb define una jerarquía de diferentes regiones que un conjunto puede ser capaz de embaldosar, como rectángulos, tiras y todo el plano, y muestra que es indecidible si los poliominós de un conjunto dado pueden embaldosar el plano , al mapear conjuntos de fichas de Wang a conjuntos de poliominós. [31]

Debido a que el problema general de agrupar regiones del plano con conjuntos de poliominós es NP-completo , [32] agrupar con más de unas pocas piezas rápidamente se vuelve intratable y, por lo tanto, se requiere la ayuda de una computadora. El enfoque tradicional para agrupar regiones finitas del plano utiliza una técnica en informática llamada retroceso . [33]

En Jigsaw Sudokus, una cuadrícula cuadrada está cubierta de regiones con forma de poliominó (secuencia A172477 en la OEIS ).

Teselación de regiones con copias de un único poliominó

Otra clase de problemas pregunta si las copias de un poliominó dado pueden teselar un rectángulo y, si es así, qué rectángulos pueden teselar. [34] Estos problemas han sido estudiados extensamente para poliominós particulares, [35] y hay tablas de resultados disponibles para poliominós individuales. [36] Klarner y Göbel demostraron que para cualquier poliominó hay un conjunto finito de rectángulos primos que tesela, de modo que todos los demás rectángulos que tesela pueden ser teselados por esos rectángulos primos. [37] [38] Kamenetsky y Cooke demostraron cómo varios poliominós disjuntos (llamados "agujereados") pueden teselar rectángulos. [39]

Además de los rectángulos, Golomb dio su jerarquía para los poliominós individuales: un poliominó puede teselar un rectángulo, una media tira, una tira doblada, una copia ampliada de sí mismo, un cuadrante, una tira, un semiplano , todo el plano, ciertas combinaciones o ninguna de ellas. Hay ciertas implicaciones entre ellas, tanto obvias (por ejemplo, si un poliominó tesela el semiplano, entonces tesela todo el plano) como menos obvias (por ejemplo, si un poliominó tesela una copia ampliada de sí mismo, entonces tesela el cuadrante). Los poliominós de tamaño hasta 6 se caracterizan en esta jerarquía (con el estado de un hexominó, que más tarde se descubrió que tesela un rectángulo, sin resolver en ese momento). [40]

En 2001, Cristopher Moore y John Michael Robson demostraron que el problema de teselar un poliominó con copias de otro es NP-completo . [41] [42]

Teselación del plano con copias de un único poliominó

Los dos nonominós de mosaico que no satisfacen el criterio de Conway.

También se ha discutido mucho sobre el teselado del plano con copias de un único poliominó. En 1965 se observó que todos los poliominós hasta los hexominós [43] y todos los heptominós menos cuatro teselados del plano. [44] David Bird estableció entonces que todos los octominós menos 26 teselados del plano. [45] Rawsthorne descubrió que todos los poliominós de tamaño 9 menos 235 teselados, [46] y Rhoads y otros extendieron estos resultados a áreas mayores (hasta tamaño 14) [47] y otros. Los poliominós que teselados del plano se clasificaron por las simetrías de sus teselados y por el número de aspectos (orientaciones) en los que aparecen los teselados en ellos. [48] [49]

El estudio de qué poliominós pueden teselar el plano se ha facilitado utilizando el criterio de Conway : a excepción de dos nonominós, todos los poliominós de teselación hasta un tamaño 9 forman un parche de al menos una tesela que lo satisface, siendo más frecuentes las excepciones de tamaño mayor. [50]

Varios poliominós pueden teselar copias más grandes de sí mismos, y repetir este proceso recursivamente da como resultado un teselado de rep-tiles del plano. Por ejemplo, para cada entero positivo n , es posible combinar n 2 copias del L-trominó, L-tetrominó o P-pentominó en una única forma más grande similar al poliominó más pequeño del que se formó. [51]

Teselación de una figura común con varios poliominós

Una cifra de compatibilidad mínima para los pentominós T y W.

El problema de compatibilidad consiste en tomar dos o más poliominós y encontrar una figura que pueda ser teselada con cada uno de ellos. La compatibilidad de poliominós ha sido ampliamente estudiada desde la década de 1990. Jorge Luis Mireles y Giovanni Resta han publicado sitios web de resultados sistemáticos, [52] [53] y Livio Zucca muestra resultados para algunos casos complicados como tres pentominós diferentes. [54] El problema general puede ser difícil. La primera figura de compatibilidad para los pentominós L y X se publicó en 2005 y tenía 80 teselas de cada tipo. [55] Se ha demostrado que muchos pares de poliominós son incompatibles por agotamiento sistemático. No se conoce ningún algoritmo para decidir si dos poliominós arbitrarios son compatibles.

Poliominós en rompecabezas y juegos

Además de los problemas de teselación descritos anteriormente, existen juegos matemáticos recreativos que requieren doblar un poliominó para crear otras formas. Gardner propuso varios juegos simples con un conjunto de pentominós libres y un tablero de ajedrez. Algunas variantes del sudoku utilizan regiones con forma de no-nominó en la cuadrícula. El videojuego Tetris se basa en los siete tetrominós de un solo lado (que se escriben "Tetriminos" en el juego), y el juego de mesa Blokus utiliza todos los poliominós libres hasta los pentominós.

Etimología

La palabra polyomino y los nombres de los distintos tamaños de polyomino son todos retroformaciones de la palabra domino , una pieza de juego común que consta de dos cuadrados. Se cree que el nombre domino para la pieza de juego proviene de la prenda de mascarada con manchas domino , del latín dominus . [56] A pesar de este origen de la palabra, al nombrar poliominós, la primera letra d- de domino se interpreta fantasiosamente como una versión del prefijo di- que significa "dos", y se reemplaza por otros prefijos numéricos .

Véase también

  • Teoría de la percolación , estudio matemático de subconjuntos aleatorios de cuadrículas de números enteros. Los componentes finitos y conectados de estos subconjuntos forman poliominós.
  • Diagrama de Young , un tipo especial de poliominó utilizado en teoría de números para describir particiones de números enteros y en teoría de grupos y aplicaciones en física matemática para describir representaciones del grupo simétrico.
  • Blokus , un juego de mesa que utiliza poliominós.
  • Cuadrángulo , un tipo de gráfico no dirigido que incluye como caso especial los gráficos de vértices y aristas de poliominós.
  • Polycube , su análogo en tres dimensiones.

Notas

  1. ^ Golomb ( Polyominoes , Prefacio a la primera edición) escribe "la observación de que hay doce patrones distintivos (los pentominós) que pueden formarse con cinco piedras conectadas en un tablero de Go ... se atribuye a un antiguo maestro de ese juego".
  2. ^ Golomb, Solomon W. (1994). Poliominós (2.ª ed.). Princeton, Nueva Jersey: Princeton University Press. ISBN 978-0-691-02444-8.
  3. ^ Gardner, M. (noviembre de 1960). "Más sobre las formas que se pueden crear con fichas de dominó complejas (juegos matemáticos)". Scientific American . 203 (5): 186–201. doi :10.1038/scientificamerican1160-186. JSTOR  24940703.
  4. ^ Whittington, SG; Soteros, CE (1990). "Animales reticulares: resultados rigurosos y conjeturas arriesgadas". En Grimmett, G.; Welsh, D. (eds.). Desorden en sistemas físicos . Oxford University Press.
  5. ^ Grünbaum, Branko ; Shephard, GC (1987). Mosaicos y patrones . Nueva York: WH Freeman and Company. ISBN 978-0-7167-1193-3.
  6. ^ Redelmeier, D. Hugh (1981). "Contar poliominós: otro ataque más". Matemáticas discretas . 36 (2): 191–203. doi : 10.1016/0012-365X(81)90237-5 .
  7. ^ Golomb, capítulo 6
  8. ^ Iwan Jensen. «Series de animales enrejados o poliominós». Archivado desde el original el 12 de junio de 2007. Consultado el 6 de mayo de 2007 .
  9. ^ "Actas de 2024 del Simposio sobre Ingeniería de Algoritmos y Experimentos (ALENEX) - Contando poliominós, revisitado".
  10. ^ Tomás Oliveira e Silva. "Enumeraciones de animales en el teselado euclidiano {4,4}". Archivado desde el original el 23 de abril de 2007. Consultado el 6 de mayo de 2007 .
  11. ^ "Cuadrado Mágico Armónico, Enumeración de Poliominós considerando la simetría" (PDF) .
  12. ^ "Contar poliominós de tamaño 50" (PDF) .
  13. ^ de Redelmeier, sección 3
  14. ^ Redelmeier, D. Hugh (1981). "Contando poliominós: otro ataque más". Matemáticas discretas . 36 (2): 191–203. doi : 10.1016/0012-365X(81)90237-5 .
  15. ^ Golomb, págs. 73-79
  16. ^ Redelmeier, sección 4
  17. ^ Redelmeier, sección 6
  18. ^ Jensen, Iwan (febrero de 2001). "Enumeraciones de animales y árboles en red". Revista de física estadística . 102 (3–4): 865–881. arXiv : cond-mat/0007239 . Código Bibliográfico :2001JSP...102..865J. doi :10.1023/A:1004855020556. S2CID  10549375.
  19. ^ Conway, Andrew (1995). "Enumeración de series de percolación 2D mediante el método de red finita: teoría". Journal of Physics A: Mathematical and General . 28 (2): 335–349. Bibcode :1995JPhA...28..335C. doi :10.1088/0305-4470/28/2/011. Zbl  0849.05003.
  20. ^ Jensen, Iwan; Guttmann, Anthony J. (2000). "Estadísticas de animales reticulares (poliominós) y polígonos". Journal of Physics A: Mathematical and General . 33 (29): L257–L263. arXiv : cond-mat/0007238v1 . Código Bibliográfico :2000JPhA...33L.257J. doi :10.1088/0305-4470/33/29/102. S2CID  6461687.
  21. ^ Barequet, Gill; Rote, Gunter; Shalah, Mira. "λ > 4: Un límite inferior mejorado en la constante de crecimiento de poliominós". Comunicaciones de la ACM . 59 (7): 88–95. doi :10.1145/2851485.
  22. ^ ab Barequet, Gill; Shalah, Mira (2022). "Límites superiores mejorados en las constantes de crecimiento de poliominós y policubos". Algorithmica . 84 (12): 3559–3586. arXiv : 1906.11447 . doi : 10.1007/s00453-022-00948-6 .
  23. ^ Klarner, DA; Rivest, RL (1973). "Un procedimiento para mejorar el límite superior del número de n-óminos" (PDF) . Revista canadiense de matemáticas . 25 (3): 585–602. CiteSeerX 10.1.1.309.9151 . doi :10.4153/CJM-1973-060-4. S2CID  121448572. Archivado desde el original (PDF de la versión del informe técnico) el 2006-11-26 . Consultado el 2007-05-11 . 
  24. ^ Wilf, Herbert S. (1994). Generatingfunctionology (2.ª ed.). Boston, MA: Academic Press. pág. 151. ISBN 978-0-12-751956-2.Zbl 0831.05001  .
  25. ^ Bousquet-Mélou, Mireille (1998). "Nuevos resultados enumerativos en animales dirigidos bidimensionales". Matemáticas discretas . 180 (1–3): 73–106. doi : 10.1016/S0012-365X(97)00109-X .
  26. ^ Delest, M.-P. (1988). "Funciones generadoras para poliominós columna-convexos". Journal of Combinatorial Theory, Serie A . 48 (1): 12–31. doi : 10.1016/0097-3165(88)90071-4 .
  27. ^ Bousquet-Mélou, Mireille ; Fédou, Jean-Marc (1995). "La función generadora de poliominós convexos: La resolución de un sistema q-diferencial". Matemáticas discretas . 137 (1–3): 53–75. doi : 10.1016/0012-365X(93)E0161-V .
  28. ^ Picciotto, Henri (1999), Laboratorios de geometría, MathEducationPage.org, p. 208.
  29. ^ Martin, George E. (1996). Poliominós: una guía para resolver problemas y acertijos en mosaico (2.ª ed.). Asociación Matemática de Estados Unidos . ISBN 978-0-88385-501-0.
  30. ^ CB Haselgrove; Jenifer Haselgrove (octubre de 1960). "Un programa informático para pentominós" (PDF) . Eureka . 23 : 16–18.
  31. ^ Golomb, Solomon W. (1970). "Teselación con conjuntos de poliominós". Journal of Combinatorial Theory . 9 : 60–71. doi : 10.1016/S0021-9800(70)80055-2 .
  32. ^ ED Demaine; ML Demaine (junio de 2007). "Rompecabezas, emparejamiento de aristas y empaquetamiento de poliominós: conexiones y complejidad". Graphs and Combinatorics . 23 : 195–208. doi :10.1007/s00373-007-0713-4. S2CID  17190810.
  33. ^ SW Golomb; LD Baumert (1965). "Programación de retroceso". Revista de la ACM . 12 (4): 516–524. doi : 10.1145/321296.321300 .
  34. ^ Golomb, Polyominós , capítulo 8
  35. ^ Reid, Michael. "Referencias para poliominós rectificables". Archivado desde el original el 16 de enero de 2004. Consultado el 11 de mayo de 2007 .
  36. ^ Reid, Michael. "Lista de rectángulos primos conocidos para varios poliominós". Archivado desde el original el 16 de abril de 2007. Consultado el 11 de mayo de 2007 .
  37. ^ Klarner, DA; Göbel, F. (1969). "Cajas de embalaje con figuras congruentes". Indagaciones Mathematicae . 31 : 465–472.
  38. ^ Klarner, David A. (febrero de 1973). "A Finite Basis Theorem Revisited" (PDF) . Informe técnico de la Universidad de Stanford STAN-CS-73–338. Archivado desde el original (PDF) el 23 de octubre de 2007. Consultado el 12 de mayo de 2007 .
  39. ^ Kamenetsky, Dmitry; Cooke, Tristrom (2015). "Teselación de rectángulos con poliominós perforados". arXiv : 1411.2699 [cs.CG].
  40. ^ Golomb, Solomon W. (1966). "Teselación con poliominós". Revista de teoría combinatoria . 1 (2): 280–296. doi : 10.1016/S0021-9800(66)80033-9 .
  41. ^ Moore, Cristopher ; Robson, John Michael (2001). "Problemas de mosaicos difíciles con mosaicos simples" (PDF) . Archivado desde el original (PDF) el 17 de junio de 2013.
  42. ^ Petersen, Ivars (25 de septiembre de 1999), "Math Trek: Tiling with Polyominoes", Science News , archivado desde el original el 20 de marzo de 2008 , consultado el 11 de marzo de 2012.
  43. ^ Gardner, Martin (julio de 1965). "Sobre la relación entre las matemáticas y los patrones ordenados del arte óptico". Scientific American . 213 (1): 100–104. doi :10.1038/scientificamerican1265-100.
  44. ^ Gardner, Martin (agosto de 1965). "Reflexiones sobre la tarea de comunicación con organismos inteligentes en otros mundos". Scientific American . 213 (2): 96–100. doi :10.1038/scientificamerican0865-96.
  45. ^ Gardner, Martin (agosto de 1975). "Más sobre el teselado del plano: las posibilidades de los poliominós, polidiamantes y polihexágonos". Scientific American . 233 (2): 112–115. doi :10.1038/scientificamerican0875-112.
  46. ^ Rawsthorne, Daniel A. (1988). "Complejidad de teselación de n-ominós pequeños (n<10)". Matemáticas discretas . 70 : 71–75. doi : 10.1016/0012-365X(88)90081-7 .
  47. ^ Rhoads, Glenn C. (2003). Teselación plana y búsqueda de un prototipo aperiódico . Tesis doctoral, Universidad Rutgers.
  48. ^ Grünbaum y Shephard, sección 9.4
  49. ^ Keating, K.; Vince, A. (1999). "Teselación poliominó isoédrica del plano". Geometría discreta y computacional . 21 (4): 615–630. doi : 10.1007/PL00009442 .
  50. ^ Rhoads, Glenn C. (2005). "Teselación plana mediante poliominós, polihexágonos y polidiamantes". Revista de Matemática Computacional y Aplicada . 174 (2): 329–353. Bibcode :2005JCoAM.174..329R. doi : 10.1016/j.cam.2004.05.002 .
  51. ^ Niţică, Viorel (2003). "Rep-tiles revisados". MASA selecta . Providence, RI: Sociedad Estadounidense de Matemáticas. págs. 205-217. SEÑOR  2027179.
  52. ^ Mireles, JL, "Poly2ominoes"
  53. ^ "Resta, G., "Polypolyominoes"". Archivado desde el original el 22 de febrero de 2011. Consultado el 2 de julio de 2010 .
  54. ^ "Zucca, L." Triple Pentominoes"" . Consultado el 20 de abril de 2023 .
  55. ^ Barbans, Uldis; Cibulis, Andris; Lee, Gilbert; Liu, Andy; Wainwright, Robert (2005). "Teoría de números poliominós (III)". En Cipra, Barry Arthur ; Demaine, Erik D.; Demaine, Martin L.; Rodgers, Tom (eds.). Homenaje a un matemático . Wellesley, MA: AK Peters. págs. 131–136. ISBN. 978-1-56881-204-5.
  56. ^ Oxford English Dictionary , 2.ª edición, entrada dominó
  • Mosaicos de rectángulos finitos poliomino de Karl Dahlke
  • Una implementación y descripción del método de Jensen
  • Un artículo que describe las estimaciones modernas (PS)
  • Weisstein, Eric W. "Poliomino". MundoMatemático .
  • MathPages – Notas sobre la enumeración de poliominós con varias simetrías
  • Lista de problemas de disección en Fairy Chess Review
  • Tetradas de Karl Scherer, Proyecto de Demostraciones Wolfram .
Obtenido de "https://es.wikipedia.org/w/index.php?title=Poliominó&oldid=1253989981#Poliominós_libres,_unilaterales_y_fijos"